古建筑彩绘梁整像素位移自适应搜索解算方法

刘纲 李孟珠 蒋伟 张维庆

摘   要：通过在构件表面喷涂均匀散斑并拍摄变形前后的图片，采用数字图像相关法（DIC）可实现构件位移的非接触式测量. 针对古建筑木梁彩绘图案灰度不均，导致传统DIC在整像素位移解算时识别效果差、计算效率低的难题，提出修正的自适应十字模式搜索法（IARPS）进行整像素位移解算. 首先，预估第一个搜索点的搜索半径，在该半径内进行穷举搜索;然后引入自适应十字模式算法，通过小菱形搜索实现整像素位移的解算. 采用散斑图模拟位移及装饰有彩绘图案的木梁压弯实验，将IARPS与DIC中常用粗-细搜索算法进行对比，结果表明，IARPS方法能有效克服粗-细搜索算法局部计算不精确的缺陷，且IARPS的计算效率可提高71.6%，为将DIC应用于古建筑彩绘梁的非接触式位移测量提供了一种新的解算方法.

关键词：古建筑彩绘梁;数字图像相关法;局部穷举;自适应搜索;整像素

中图分类号：TP274                               文献标志码：A

Adaptive Search Algorithm Method of Whole-pixel

Deformation for Ancient Building Painted Beams

LIU Gang1，2?，LI Mengzhu2，JIANG Wei2，ZHANG Weiqing2

（1. Key Laboratory of New Technology for Construction of Cities in Mountain Area （Chongqing University）

of the Ministry of Education，Chongqing 400045，China;

2. School of Civil Engineering，Chongqing University，Chongqing 400045，China）

Abstract：Digital image correlation method （DIC） can realize non-contact displacement measurement of member by spraying uniform speckle on member surface and taking pictures before and after deformation. Considering the problems of poor recognition effect and low calculation efficiency in deformation measurement of traditional integral pixel algorithm for  ancient building painted beams caused by painted pattern uneven gray scale， an Improve-Adaptive Rood Pattern Search （IARPS） method is proposed to calculate the entire pixel displacement. Firstly， the search radius of the first search point is estimated， and an exhaustive search is performed within the radius.  Then， Adaptive Rood Pattern Search was introduced to search the whole pixel displacement through small diamond search. By using simulated speckle pattern displacement and the bending test of common regular painted pattern decorative wood beam， IARPS is compared with the coarse-fine search method commonly used in DIC. Through comparative analysis， the results show that IARPS method can effectively overcome the imprecision of local computation in the coarse-fine search method， and the calculation efficiency can be improved by 71.6%， which  provides a new method to apply DIC to non-contact deformation measurement of ancient painted beams.

Key words：ancient painted beams;digital image correlation method;local exhaustively search;adaptive search;whole-pixel

中國古建筑具有悠久的历史传统，是当时科学技术水平和人民社会生活状况的真实见证，具有重要的历史、艺术和科学价值[1]. 在以木结构为主的古建筑中，受木材蠕变、腐蚀、虫蛀和长期荷载作用[2-3]，木质构件变形过大问题较为普遍[4]，木结构变形监测可用于判断变形发展趋势、提供结构受力计算所需变形数据，是古建筑木结构预防性保护的重要手段.

传统上古建筑变形测量以接触式方法为主，例如在结构构件上布置观测点或粘贴光纤传感器[4-5]，这些方法对古建筑构件有一定程度的破坏，不利于古建筑保护. 虽然近年来无需在古建筑上布设测试点的免棱镜技术得到快速发展，但是其测试精度受较多因素限制，在部分条件下较难满足工程测试要求. 近年来，非接触式变形测量方法得到快速发展，其中，基于数字图像相关 （Digital image correlation，DIC）原理[6]的测试方法随着摄像技术、计算能力的提升得到了大力发展，已在航天、机械和土木工程领域得到实际应用. DIC法最早可追溯到20世纪80年代，美国南卡罗莱纳大学Peters等[7]针对材料表面均匀拉伸应变测量提出基于DIC进行位移测量的思路;Sutton等[8]针对全场平面内变形的整像素位移搜索，提出粗-细搜索法，从而提高整像素级图像匹配的计算速度. Gencturk等[9]将DIC法应用于预应力混凝土位移测量，结果表明该方法可准确测量预应力混凝土变形信息. 奥村运明等[10]应用DIC法进行古建筑墙体裂缝观测，结果显示该方法能满足工程上裂缝测量的要求.

DIC法通过在被测结构表面喷涂具有一定特征的散斑图，然后利用结构位移前后散斑图的变化来识别结构变形[11]，而中国古建筑木结构的表面往往装饰有彩绘图案[12]，故利用彩绘图也可实现位移测量. 但应指出的是，与特制散斑图相比，彩绘图灰度梯度分布不均且存在大块灰度近似区，故直接采用现有DIC位移解算方法将无法保证位移测试精度. 针对这一问题，在现有自适应十字模式搜索方法（Adaptive Rood Pattern Search，ARPS）的基础上，提出局部穷举-自适应十字模式搜索方法（Improve-APRS，IARPS），提高整像素位移搜索精度，从而增强古建筑彩绘图位移辨识精度，并提升位移辨识计算的稳定性和效率. 通过实验验证所提方法的适用性，并与常用整像素位移解算方法进行对比，为古建筑木结构非接触式位移测量提供新的解算方法.

1   基于DIC原理的位移测试

1.1   位移测试原理

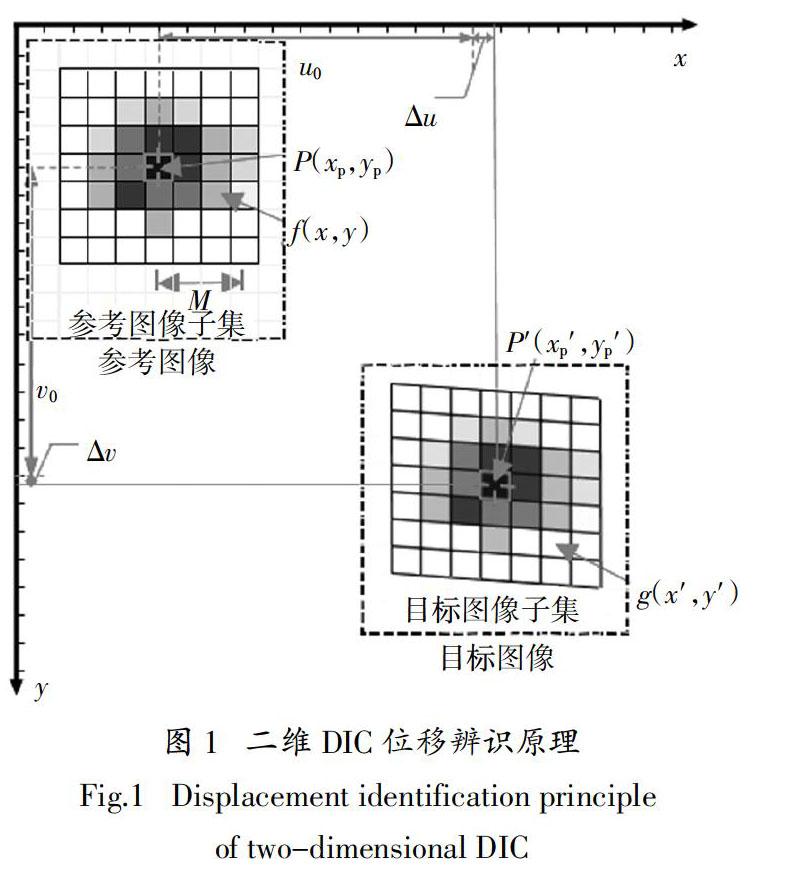
基于DIC原理的位移测试技术在被测构件上喷涂特制散斑图，借用数字摄影技术将散斑图在相机感光组件上成像，然后通过匹配变形前后数字图像像素的变化，从而获得被测物体表面各点的位移信息，该方法的位移辨识原理如图1所示.

在图1中，一个小方格代表数字图像上的一个像素，变形前的图像称为参考图像，变形后的图像称为目标图像. 针对参考图像、目标图像建立统一的坐标系x-y，参考图像中 （x，y）处像素点的灰度值为f（x，y）;目标图像中（x′，y′）处的像素点灰度值为g（x′，y′）. 设参考图像中P点坐标为（xp，yp），目标图像中与P点对应的P′点坐标为（x′p，y′p），DIC方法计算P′点到P的距离可分为以下几个步骤：

1）在參考图像中，选取整数M，然后选择一个计算点P（xp，yp），以该点为中心选取（2M+1）×（2M+1） 像素大小的区域为计算子集，其中2M+1称为子集半径.

2）在目标图像中，任选一点并作为搜索点，以该点为中心，框选（2M+1）×（2M+1）的计算子集，再计算相关系数CZNSSD：

式中：fm表示参考图像子集的灰度平均值;gm表示目标图像子集的灰度平均值. 然后，通过一定的搜索方法计算多个点的相关系数，并将相关系数最值点对应的搜索点作为P′点的匹配点. 此时，可确定P点整像素x向位移up、y向位移vp .

3）根据求得的匹配点的坐标，在（xp + up，yp + vp）像素点相邻1个像素范围内通过一定方法进行亚像素位移搜索，得到P点分别在x、y向亚像素位移Δup、Δvp .

4）根据求得的整、亚像素位移，最终解算得到P点x向位移u、y向位移v分别为：

从以上步骤可知，DIC法先执行整像素位移搜索，并将搜索结果作为亚像素搜索的初始值，故整像素搜索算法不但决定整像素搜索精度，也将影响亚像素搜索精度. 因此，整像素搜索算法对位移辨识精度的影响较大.

需指出的是，第一次在目标图像中任选一点时，若该点距图像边缘的距离小于2M+1，则无法以该点为中心组成计算子集，称为边缘问题. 为避免这一问题，可在初次选择计算点时进行预判：若计算点不存在边缘问题，则进行以上步骤的搜索;若不满足，则重新选取计算点，直至找到不存在边缘问题的计算点.

1.2   整像素粗-细搜索算法

目前，DIC中最常用的整像素位移搜索算法有粗-细搜索法（Coarse-Fine Search，CFS）[13]、三步搜索法[14]及菱形搜索法[15]等，其中CFS算法的精度和计算效率相对较高，其位移搜索的基本思路为：将整个目标图像视为搜索区域，首先采用较大的计算步长计算相关系数，以相关系数极小值对应的搜索点为本轮搜索的匹配点;然后以此匹配点为中心，缩小搜索区域及计算步长选取搜索点进行下一轮搜索;最后，当计算步长缩小为1像素时，可得P′点的匹配点，进而计算得到该点的整像素位移.

1.3   搜索算法精度评价指标

设参考图像和目标图像的像素均为I × K，则两幅图像的均方误差MES定义为：

两幅图像的峰值信噪比（Peak-Signal-to-Noise-Ratio，PSNR）定义为：

式中：MAXI表示图像灰度的最大值，对于采样点用8进制表示的灰度图像取255. 峰值信噪比可评价两幅图像子集的近似性，近似程度越高，PSNR系数越高，即搜索算法的精度越高.

2   修正的自适应十字模式整像素搜索法

2.1   自适应十字模式整像素搜索法

CFS算法假定每一轮最佳匹配点处的相关函数值CZNSSD单调减小，即由相关系数组成的二维曲面是单峰的. 通常情况下，由散斑图得到的二维曲面可能存在几个局部极值现象，如图2（a）所示. 此时，只要计算步长选择合适，CFS仍可搜索到正确结果. 但对于彩绘图像，由于其灰度分布不均，所得相关函数曲面往往存在多峰现象，在CFS搜索过程中的单调性不复存在，如图2（b）所示. 此时，初始计算步长对CFS算法精度甚至正误影响很大，而初始计算步长通常由人工主观选取，具有很大的随机性.

为克服计算步长选取的随机性，Nie等[16]提出了自适应十字模式搜索法（Adaptive Rood Pattern Search，ARPS）. 其基本思路是，假設物体的变形是连续的，在进行整像素位移搜索时，采用相邻已知位移像素点的位移作为搜索初值，其具体搜索步骤为：

1）对参考图像中的某计算点P，设其在x-y坐标系中的坐标为（u1，v1）;记P相邻像素点已知整像素位移为（u，v），记R = max（|u|，|v|），R = （u，v）. 在目标图像中，以坐标（u1，v1）所在的像素点为中心点O，若是第一个计算点，则在该点沿x-y轴向相距2像素的上下左右各选1个点，形成十字形搜索模式;若不是第一个计算点，则在该点沿x-y轴向相距R像素的上下左右各选1个点，形成十字形搜索模式，同时选取R为一个搜索点，共计5个搜索点，如图3（a）中黑色小圆点所示.

2）按式（1）计算图3（a）中5个搜索点的相关系数，选取相关系数最小值所在点为初始匹配点. 以初始匹配点为中心，选取该点及上下左右4个相邻像素点形成单位十字搜索模式，并将这5个点作为新的搜索点，如图3（b）所示.

3）按式（1）计算单位十字搜索模式中5个搜索点的相关系数，若最佳匹配位置为单位十字搜索模式的中心点，则结束搜索，该点即为计算点P的最佳匹配点P′（u2，v2）;否则，将单位十字中心移至新的相关系数最小点，重复进行单位十字模式搜索，直至相关系数最小点为十字搜索模式的中心为止，此时十字模式的中心点即为计算点的最佳匹配点P′.

4）根据求得的最佳匹配点P′的坐标（u2，v2），可解算P点的整像素位移（u2 - u1，v2 - v1）.

当计算参考图像中的第一点时，其相邻点位移为未知，故在第1）步中仅采用十字形搜索模式的4个点进行搜索，其余步骤与以后各计算点的步骤相同.

2.2   基于局部穷举的自适应十字模式搜索法

ARPS法根据相邻像素已知位移自适应调整步长，有利于解决相关系数曲面存在多个极值的问题，但对第一个位移搜索点的位移初值采取零位移假设（仅采用4个搜索点进行计算），可能带来一定的误差. 为解决该问题，可先预估第一个位移搜索点的位移最大值，并将其作为初始搜索半径，进行局部穷举搜索，从而为后续各搜索点的位移计算提供准确的初值. 局部穷举搜索具体步骤为：

1）对于参考图形中的某搜索点P，已知其在x-y坐标系中的坐标为（u1，v1）;在目标图像中，以坐标（u1，v1）所在的点为中心点，选择一个初始搜索半径，如图3（c）所示，在该方形区域内对每个点进行局部穷举搜索.

2）针对方形区域内的每一个点，计算所有点的相关系数.

3）选取所有搜索点中相关系数最小点为第一个初始计算点的最佳匹配点，然后按照ARPS法的第2）～4）步计算该点位移.

4）按照ARPS方法的第1）～4）步计算剩余各计算点的位移.

采用穷举搜索可确保搜索到精确的位移初始向量，避免陷入图2（b）所示的错误局部最优解，将增加局部穷举搜索后的ARPS法称为修正的自适应十字模式搜索法（Improved-ARPS，IARPS）.

3   实验验证

3.1   实验设置

分别通过模拟散斑图发生刚体位移、实验室木梁彩绘图变形实验对比IARPS算法与CFS、ARPS算法的区别.

3.1.1   散斑图位移模拟

采用Zhou等[17]提出的散斑图生成算法得到256 × 256像素的散斑图作为参考图像，其中高斯光斑数目为1 000个，高斯光斑大小为4像素，高斯光斑的中心光强为0.7. 将参考图像在y向移动6个像素作为目标图像，即目标图像各整像素点的位移向量均为（0，6）. 为模拟测试噪声，在目标图像中加入均值为0，标准差为2的高斯白噪声. 为节约篇幅，将参考图像、目标图像分左右两幅给出，如图4所示.

在散斑图中，仅计算图4中虚线所在像素点发生的位移，该虚线由90个像素点组成，其像素坐标自上而下定义为1～90 pixel.

3.1.2   彩绘图实验

在实验室中采用长宽高分别为2 000 mm×40 mm×25 mm的木梁进行实验，将规则花纹粘贴于梁中部侧面. 采用重物分两次在跨中加载，使梁产生挠度，分别记为工况1和工况2，并在跨中安装千分表对辨识位移的精度进行验证，具体的加载装置如图5所示. 实验中采用的图像采集系统为VIC-2D，相机型号为GZL-CL-41C6M-C，其分辨率为2 048×2 048像素. 将相机放置在彩绘梁正前方约2 m处，并使其光轴对准梁的形心且与彩绘图案面垂直，将相机与计算机相连并用测试系统的软件进行图像采集.

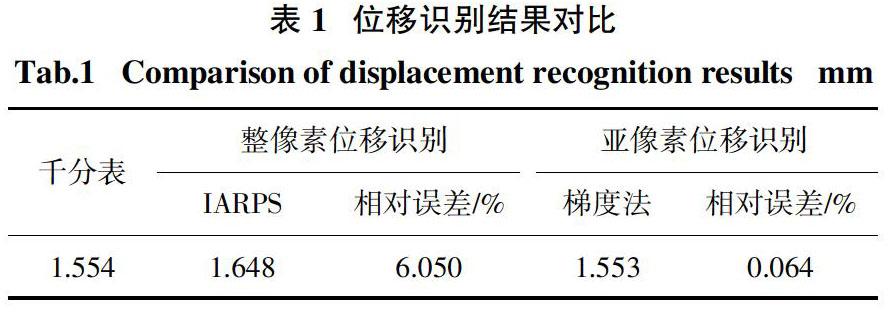
3.2   实验结果分析

考虑到穷举搜索法（Exhaustive Search，ES）将计算搜索指定范围内所有可能的像素点，其计算精度在所有的搜索算法中最好，故采用该算法作为基准验证其他整像素解算方法的精度.

[2]    GUO Z R，YANG Z F. Analysis of aseismic mechanism of wooden architecture of ancient Chinese [J]. Advanced Materials Research，2014，889/890：1417—1420.

[3]    CHEN L，WANG B. Research on digital reconstruction of Chinese ancient architecture [C]//Proceedings of 2013 International Conference on Anti-Counterfeiting，Security and Identification. Shanghai：IEEE，2014：136—139.

[4]    姜绍飞，唐伟杰，吴铭昊，等. 基于FBG应变测量的古建筑木梁变形监测方法[J]. 地震工程与工程振动，2016，36（6）：198—206.

JIANG S F，TANG W J，WU M H，et al. A deformation monitoring method of ancient wooden beam based on FBG strain measurement [J]. Earthquake Engineering and Engineering Dynamics，2016，36（6）：198—206. （In Chinese）

[5]    时以亮，施斌，童恒金，等. 分布式光纤感测技术在古建筑监测中的應用研究[C]//中国地质学会工程地质专委会. 2014年全国工程地质学术年会论文集. 太原：工程地质学报编辑部，2014：519—523.

SHI Y L，SHI B，TONG H J，et al. Application research of distributed optical fiber sensing technology in ancient architecture monitoring[C]// Engineering Geology Commission，China Geology Society. Proceedings of 2014 National Engineering Geology Academic Conference. Taiyuan：Department of Journal of Engineering Geology，2014：519—523. （In Chinese）

[6]    SCHREIER H，ORTEU J J，SUTTON M A. Image correlation for shape，motion and deformation measurements [M]. Berlin：Springer Publishing Company，2009：56—60.

[7]    PETERS W H，RANSON W F. Digital imaging techniques in experiment stress analysis [J]. Optical Engineering，1982，21（3）：427—431.

[8]    SUTTON M A，WOLTERS W J，PETERS W H，et al. Determination of displacement using an improved digital correlation method [M]. London：Butterworth & Co （Publishers） Ltd，1983：133—139.

[9]    GENCTURK B，HOSSAIN K，KAPADIA A，et al. Use of digital image correlation technique in full-scale testing of prestressed concrete structures [J]. Measurement，2014，47（1）：505—515.

[10]  奥村运明，林颖文，李宁，等. 数字图像技术在古建筑裂缝监测中的应用[J]. 河南科学，2008，26（2）：212—214.

AOCUN Y M，LIN Y W，LI N，et al. Applications of digital graphics technology in the monitoring of ancient architecture cracks [J]. Henan Science，2008，26（2）：212—214. （In Chinese）

[11]  伍卫平. 图像相关技术的亚像素位移算法与实验研究[D]. 武汉：华中科技大学力学系，2009：28—35.

WU W P. Sub-pixel displacement algorithm based on image correlation method and experiment study [D]. Wuhan：Department of  Mechanics，Huazhong University of Science & Technology，2009：28—35. （In Chinese）

[12]  林珠龙. 关于中国古建筑油漆彩绘的研究[J]. 美与时代（城市版），2018（7）：30—31.

LIN Z L. Research on the painting of Chinese ancient buildings [J]. Beauty and Times （City Edition），2018（7）：30—31. （In Chinese）

[13]  熊磊. 基于數字图像相关方法的材料拉伸变形测量技术[D]. 长春：吉林大学机械设计及理论学院，2012：13—21.

XIONG L. The measurement technology of the tensile deformation of material based on digital image correlation [D]. Changchun：College of Mechanical Design and Theory，Jilin University，2012：13—21. （In Chinese）

[14]  HASSEN W，AMIRI H. Block matching algorithms for motion estimation[C]//Proceedings of 7th IEEE International Conference on e-Learning in Industrial Electronics. Vienna，Austria：Institute of Electrical and Electronic Engineers，2014：136—139.

[15]  ZHU S，MA K K. A new diamond search algorithm for fast block-matching motion estimation[J]. IEEE Transactions on Image Processing，2000，9（2）：287—290.

[16]  NIE Y，MA K K. Adaptive rood pattern search for fast block-matching motion estimation [J]. IEEE Transactions on Image Process，2002，11（12）：1442—1449.

[17]  ZHOU P，GOODSON K E. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation [J]. Optical Engineering，2001，40（8）：1613—1620.