KoBol分数阶期权定价模型的数值方法

张灵溪，殷俊锋

（同济大学数学科学学院，上海200092）

经典的Black‐Scholes（BS）模型［1］假设标的资产的收益变化服从几何布朗运动，也就是资产的价格服从对数正态分布，设St为标的资产在t时刻的价格，r为无风险利率，σ为波动率，V(x，t)为t时刻时x= ln(St)下的期权价格，那么V(x，t)满足以下方程：

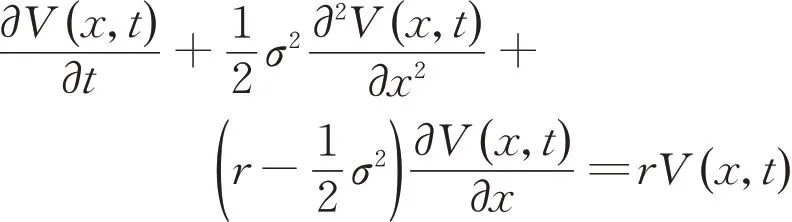
Black‐Scholes期权定价模型是金融工程中一个重大突破，为风险中性条件下的期权定价理论提供了有力的数学支撑。但是，该模型成立的前提条件非常严格，例如市场交易无摩擦，市场不存在套利机会，资产收益服从正态分布，在这种情况下由该模型计算出的结果往往与市场真实的情况不相吻合。实际市场中的隐含分布与正态分布相比存在尖峰肥尾的现象，因此在期权市场中会存在波动率微笑［2］。

为了弱化其模型假设对定价带来的影响，很多学者都在此基础上做了深入的研究。Merton［3］提出了跳跃过程服从对数正态分布的跳‐扩散模型。Kou［4］假设资产跳跃服从对数双指数分布，从而构造了相应的跳‐扩散模型。 还有随机波动率模型［5- 6］，考虑交易费用的期权定价模型［7］等。对于跳‐扩散模型［8-10］以及美式期权［11］的求解也有许多不同的数值方法。

随着研究的深入，Mandelbrot［12］发现股票的收益分布有长尾的特点，在此基础上推导出用α 稳定的列维过程代替标准的几何布朗运动，用纯无限跳跃模型来描述金融资产价格的变化，其中α< 2。在此基础上，许多学者利用列维过程来代替Black‐Scholes模型中的布朗运动，从而提出了相应基于列维过程的期权定价模型。Carr 等［13］提出FMLS(finite moment log stable)模型，可以表示标的资产对数收益的倾斜密度特征。 Koponen［14］、Boyarchenko等［15］将修正α稳定的列维过程应用在模拟标的资产的动力学特征上，称为KoBoL模型。Carr等［16］提出允许标的资产价格出现有限或者无限跳跃幅度的过程，称之为CGMY模型。近年来，这些由列维过程推导出的金融衍生品定价模型由于可以准确描述标的运动而得到广泛且深入的研究［17］。

利用分数阶模型进行期权定价时，需要求解一个分数阶对流扩散方程。Marom等［18］比较了上述3种分数阶期权定价模型定价欧式期权的数值结果，但并未给出相应的稳定性与收敛性条件。Wang等［19］给出了具有一阶精度的差分离散格式，并在障碍期权上进行定价。Meng 等［20］利用CGNR 算法对欧式看涨期权进行定价，并与Black‐Scholes 模型进行了比较。Zhang等［21］利用BiCGSTAB算法求解了单边分数阶欧式看涨定价。

本文主要研究一类双边分数阶期权定价方程的数值解法。首先对于这类双边分数阶方程的一般形式，利用带位移的Grünwald 格式，给出每个时间层上的离散格式，并分析了迭代格式的数值稳定性。然后结合KoBol 模型下迭代矩阵的特殊结构，构造了预处理Krylov子空间方法进行求解。最后，在数值实验中对欧式看涨期权进行定价，并使用国内上证50ETF与沪深300ETF场内期权数据进行实证研究，验证算法有效性的同时也体现了KoBol 模型在真实市场中的有效性。

1 基于分数阶列维过程期权定价模型

对于列维过程Xt，t ≥0，其为增量独立固定的随机过程，且路径依概率连续。不失一般性，假设X0≡0。Xt的对数特征函数有以下Lévy‐Khintchine表达式：

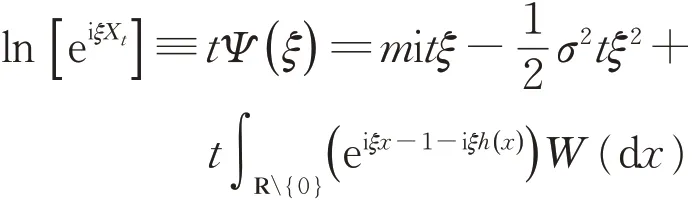
式中：m ∈R；σ ≥0；i= −1；h(x) 为截断函数。列维测度W满足以下公式：

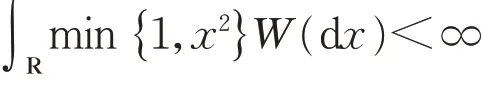
Ψ ( ξ ) 为列维过程的特征指数，列维测度W (dx ) 还可以写成W (dx) = w( x )dx，w( x ) 又称作列维密度函数。

特别地，KoBol 模型的列维密度函数为如下形式：

式中：D > 0，λ> 0，p、q∈[ −1，1]，p+ q= 1，0<α≤2。

除了KoBol 模型外，分数阶期权定价模型还有FMLS与CGMY模型，这3类模型都可以表示为如下的分数阶微分方程：

式中：x ∈(−∞，+ ∞)，t ∈(0，T)，0< α< 2，a 和d 是非负常数，函数b( x ) 和c( x ) 充分光滑，函数～f ( x )和～h( x )是连续的，且均为非负函数。∂α∂+xα与∂α∂−xα分别为Riemann‐Liouville 左分数阶微分算子与右分数阶微分算子［22］，有如下形式：

式中：α∈(n−1，n)，n 为整数，Γ(⋅)表示Gamma 函数，在本文中只考虑α∈(1，2)的情况。

KoBol模型中的相关参数可以作如下表示：

相比于BS 模型中的对数正态分布，在分数阶期权模型中，可以通过调整参数的取值，使隐含分布更接近市场的实际分布。例如在KoBol 模型中，可以通过参数α和λ调整隐含分布的峰度，参数p调整隐含分布的偏度，这样在一定程度上可以消除波动率微笑对期权定价带来的影响。

期权定价问题是一个终值问题，自变量x 定义在无界区域(−∞，∞)上，为了能够使用数值方法求解该问题，需要用合理的方法截断为x ∈[ L，R ]，参考文献［23］。在欧式期权中，终值条件与边值条件为

对于看涨期权有

首先对截断区域[ L，R ] ×[ 0，T ] 进行网格划分。 将空间层N 等分，步长h =( R−L)/N，对应的节点为xn= L+ nh，n= 0，1，…，N；将时间层M等分，步长τ = T/M，对应的节点为tm= mτ，m =0，1，…，M。函数V ( x，t )在对应节点上取值简记为V ( xn，tm)= Vmn，其余记号类似。

Meerschaert 与Tadjeran 证明了使用Grünwald格式离散分数阶扩散方程得到的迭代格式不稳定，并提出了带位移的Grünwald‐Letnikov格式［24］如下：

对方程(1)使用中心差分格式离散对流项，得到如下的半离散格式：

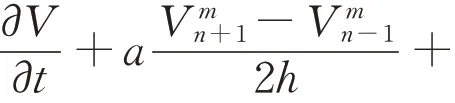
其中

对于半离散格式(3)，时间方向的采用加权隐式差分格式离散，第m层与第m + 1层的加权平均如下：

其中θ ∈[ 0，1 ]。 特别地，当θ = 1时，为显式格式

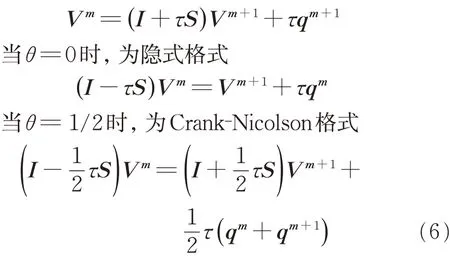
Tadjeran［25］证明了带位移的Grünwald格式在空间层上为一阶精度，又因为Crank‐Nicolson 格式在时间层上为二阶精度，那么差分格式(6)的截断误差为O (τ2)+ O( h )，所以该格式相容。在此基础上，对式(6)的稳定性做以下分析。

引理1 （Gerschgorin 圆盘定理）设A=［aij］∈Cn×n，令

解之得Re(λS) < 0。记Snn为矩阵S第n行的对角元，rn为该行所对应的圆盘半径，由式( 4) 可以得到

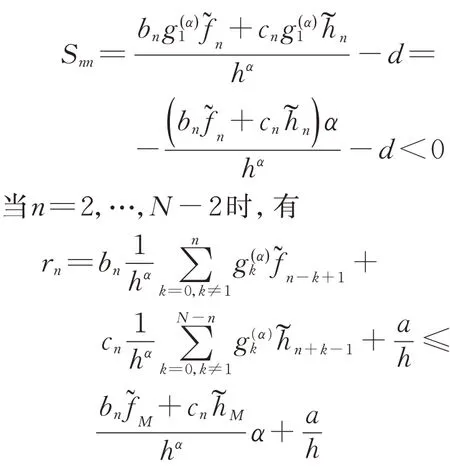
因为Re(λS) < 0，所以有Snn+ rn< 0，即

2 预处理技术

在求解大规模稀疏线性方程组时，以CG、GMRES、BiCGSTAB 和CGNR 为代表的Krylov 子空间迭代法是目前广泛使用的方法［26］，并在金融领域有广泛的应用［20-21］。这类子空间迭代法的收敛速度与迭代矩阵特征值的聚集程度有关，使用预处理方法能有效改善原线性方程组系数矩阵的性质，使得相应迭代方法的步数和求解时间大大减少，提高计算稳定性和计算效率。

预处理方法是指对于线性方程组Ax = b，其中A 为系数矩阵，b 为右端向量，x 为需要求解的向量，寻找一个非奇异矩阵H，然后应用Krylov 子空间迭代法求解以下同解线性方程组：

相应得到原算法的左预处理格式与右预处理格式，其中H称为预处理矩阵。考虑到右预处理方法不会改变GMRES 算法中的残差，在本文中使用右预处理格式。

在上节中离散得到的Crank‐Nicolson格式如下：

同时，对于KoBol模型，可以将方程(1)中的系数写成以下格式：

所以可以得到如下形式：

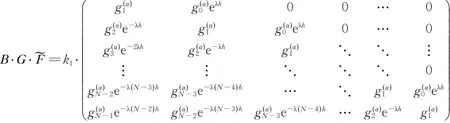
可以采用循环预处理子来加速子空间方法［27］，如Strang循环预处理子［28］与Chan循环预处理子［29］。记Tn为一个n× n 的Toeplitz 矩阵，那么Strang 循环预处理矩阵s(Tn) 是一个与Tn阶数相同的Toeplitz 矩阵，其元素可由长度为2n−1 的序列sk所决定。 其中

类似地，Chan 循环预处理矩阵c(Tn)也是一个与Tn阶数相同的Toeplitz 矩阵，其元素可由长度为2n−1的序列sk所决定。 其中

在后面的数值实验中将该预处理技术应用于GMRES、BiCGSTAB 和CGNR 算法上并比较计算效果。

3 数值实验

首先对一个带精确解的双边分数阶扩散方程来验证该离散格式的精度与收敛阶。然后，在KoBol模型下对欧式看涨期权进行定价。

例1 考虑如下终值问题：

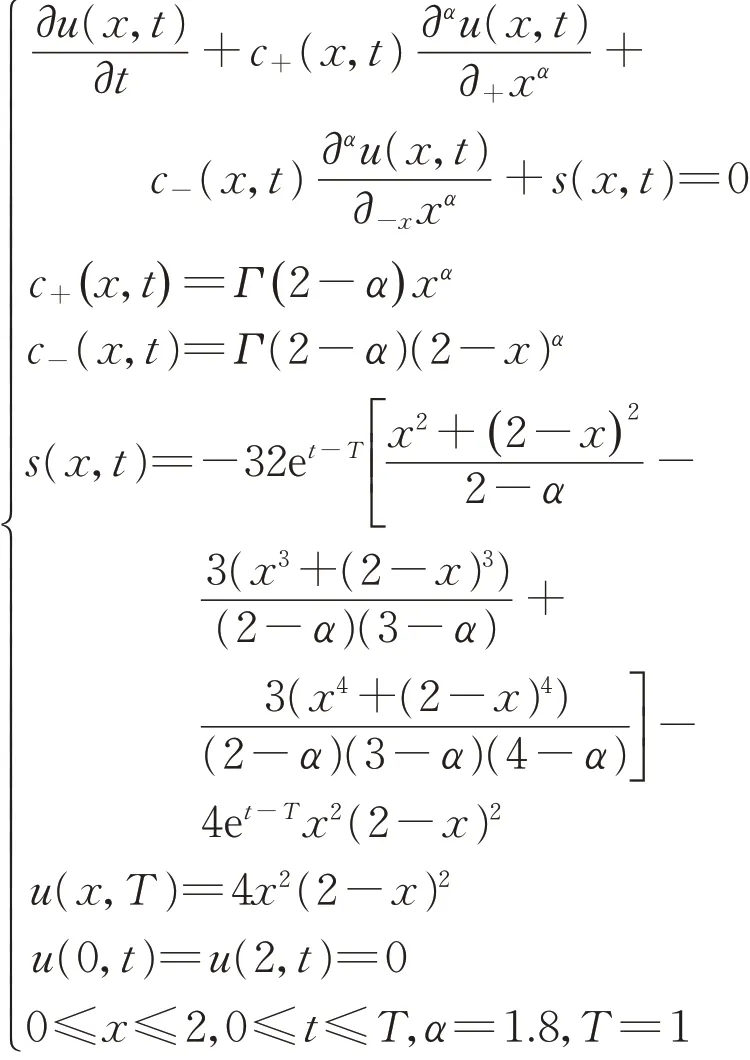
其中该方程的精确解为U(x，t) = 4et−Tx2(2−x)2。

根据前文提到的离散格式对上述方程进行差分离散，并将例1中的系数代入式(7)验证，发现此时Crank‐Nicolson 格式无条件稳定。取时的数值解与真实解如图1，并记精度误如表1。

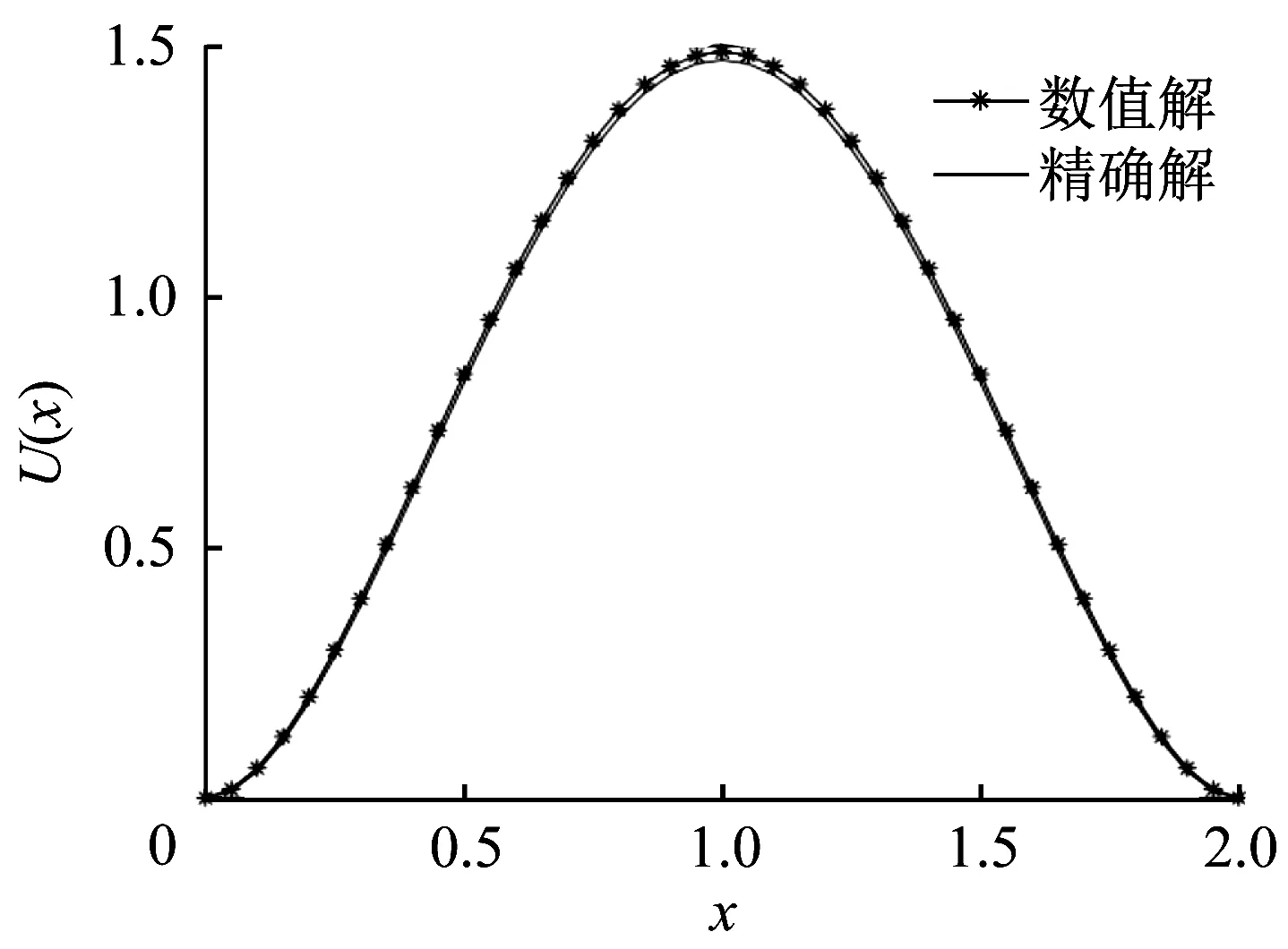
图1 例1中数值解与真实解的比较(t=0)Fig. 1 Comparison of exact solution with numerical solution for Example 1 (t=0)

例2 考虑如下欧式看涨期权KoBol模型：

表1 例1中Crank⁃Nicolson格式计算精度E∞与收敛阶Tab. 1 Numerical accuracy E∞ and conver⁃gence order of Crank⁃Nicolson scheme for Example 1

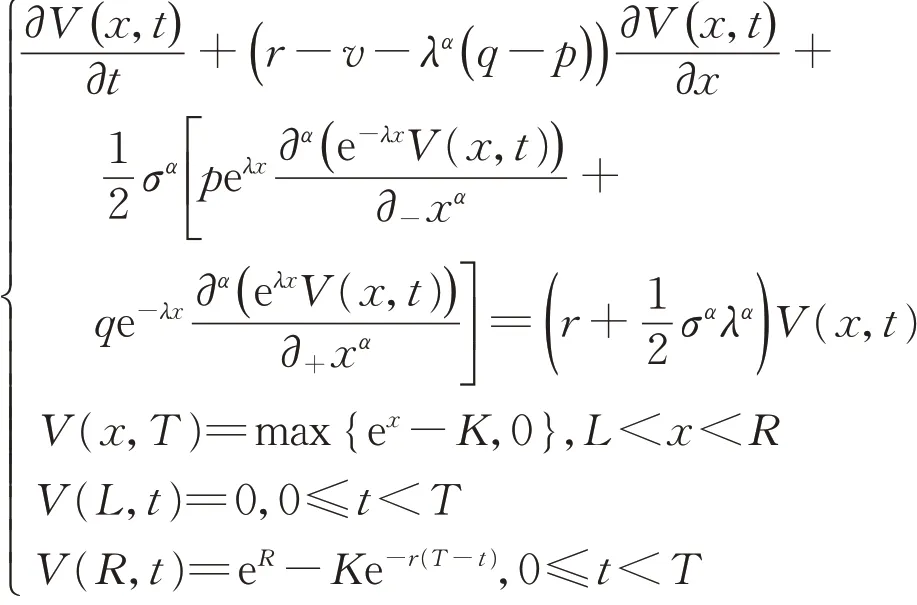
其中参数选取分别为：r= 0.05，T= 0.5，p= 0.5，q= 0.5，σ= 0.2，λ= 3，α= 1.9，K= 80，v=

例2的解曲面如图2a。将相同的期权参数利用Black‐Scholes 公式进行定价，将得出的期权价格与Kobol 模型下的做差比较如图2b，其价格在一定程度上体现了列维分布与正态分布相比具有尖峰肥尾的特点。在期权交易中，将期权分为实值期权、平值期权与虚值期权，那么，尖峰意味着在平值附近其概率分布更靠近现价，从而在相同波动率下其理论收益略低于Black‐Scholes 模型，所以价格也略低。而肥尾意味着在深度虚值与深度实值部分的理论收益高于正态分布的估计，其价格略高于Black‐Scholes模型的价格，这也与实验结果观测一致，说明该模型更接近于实际分布。

将Strang 和T. Chan 循环预处理子用在GMRES、BiCGSTAB、CGNR算法上并与未经预处理的算法作比较，在计算例2 的同时，记录每个时间层上求解线性方程组的迭代步数IT 与计算时间并取平均，其中最大迭代步数max IT= 10 000，停止准则为||rk|| ||r0|| ≤1× 10−7，实验结果见表2。

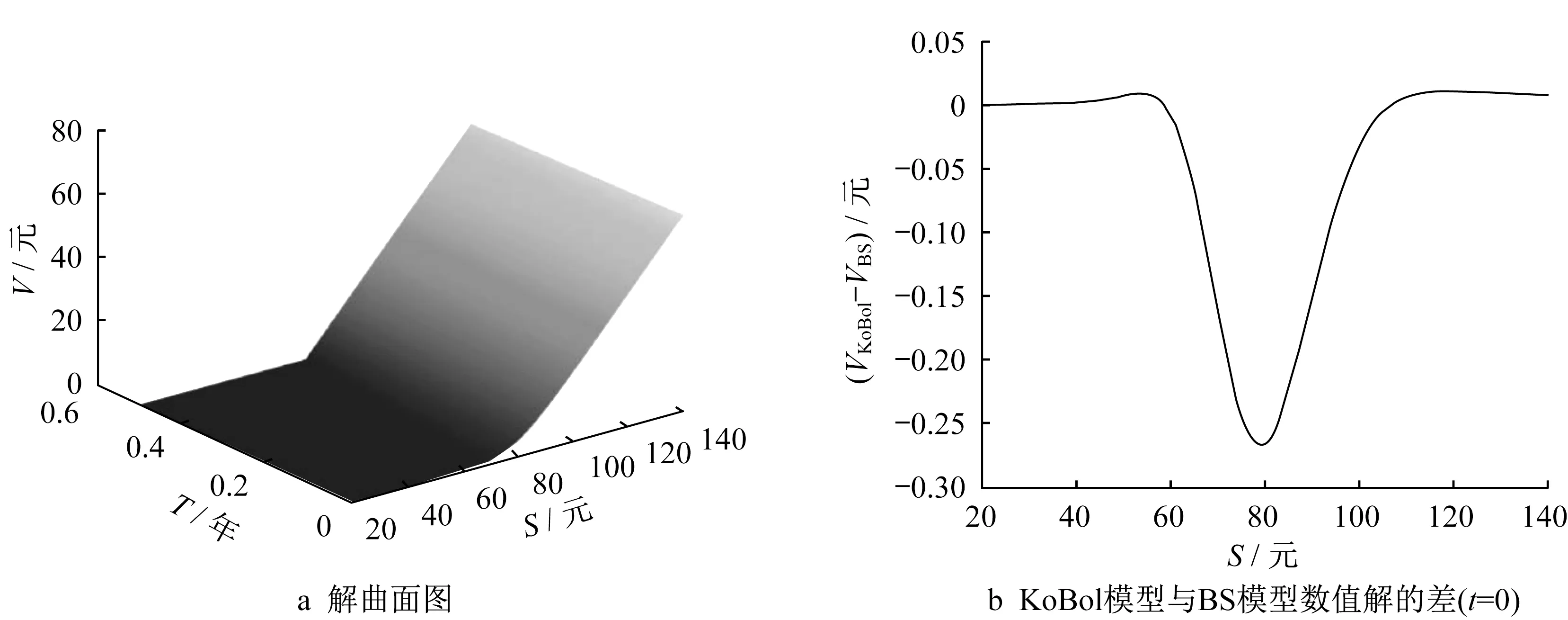
图2 例2欧式看涨期权在KoBol模型下的解Fig. 2 Solution for a European call option in KoBol model

表2 例2采用预处理子空间方法的计算结果对比Tab. 2 Numerical results of preconditioned subspace methods for Example 2

实验结果表明，无论是迭代步数还是计算时间，使用预处理技术之后的计算效率都明显优于未经预处理的算法。同时，可以发现相同条件下预处理GMRES 算法是所有算法中计算时间最快的方法。预处理技术之所以可以降低子空间算法的迭代步数，原因在于预处理之后系数矩阵的特征值较为聚集。将例2中N= 210时，经两类预处理子预处理之后的系数矩阵特征值绘制如图3 所示。可以发现，经过预处理之后的特征值确实较为聚集。

图3 例2经预处理后的系数矩阵特征值分布Fig. 3 Eigenvalue of preconditioned coefficient matrix

4 基于股指期权的实证研究

通过对中国股票市场进行研究发现，在国内股票市场也存在尖峰肥尾的现象。图4为上证50指数与沪深300指数在2019年1月至12月每日对数收益率的归一直方图与对应的正态分布概率密度函数图，可以发现在中国股票市场中，这一特点十分明显。所以Black‐Scholes模型在我国市场中进行定价时会有较大误差。接下来验证KoBol模型可以更好地描述国内期权市场。

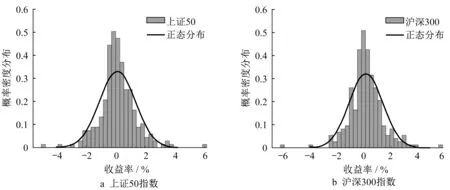
图4 2019年上证50指数与沪深300指数的尖峰肥尾现象Fig. 4 Skewed and fat tailed phenomenon of SSE 50 and CSI 300 Index in 2019

在国内的场内期权交易市场中，交易最为活跃、成交量最大的是当月合约，其买卖价差也更为接近，所以考虑上交所2020年1月3日收盘时，1月22 日到期的上证50ETF 与沪深300ETF 场内期权收盘数据。在实际交易中，市场上更多地采用Black‐Scholes模型进行定价，将比较KoBol模型及Black‐Scholes 模型的定价与市场价格之间的差距。对KoBol 与Black‐Scholes（BS）模型选取的参数如表3，标的现价S0与时间T均为市场收盘数据，无风险收益率r为1年期国债收益率。采用过去180 d的年化历史波动率作为定价模型中的波动率，年化天数为252 d，经计算得50ETF为σ= 16.74%，300ETF为σ= 17.29%。

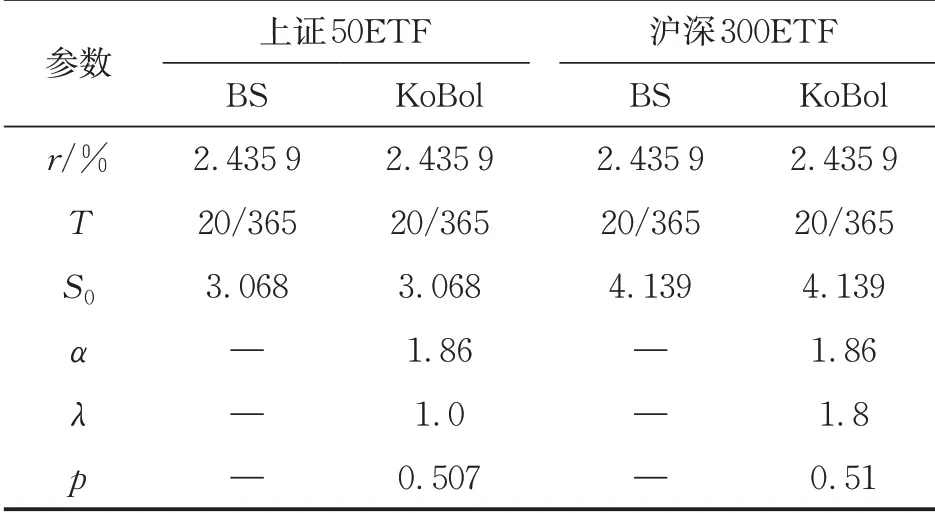
表3 KoBol模型与Black⁃Scholes模型参数选取Tab. 3 Parameter selection for Kobol model and BS model

对于Black‐Scholes模型直接利用欧式期权的解析解进行定价。用VM表示市场实际价格，用均方误差E1、相对误差E2与最大误差E∞来衡量误差大小，分别有如下形式：

两种模型的定价结果如表4与表5，与市场价格作差取绝对值之后的结果见表6 与表7。可以看出KoBol模型下的误差相比Black‐Scholes 模型都要更小，说明KoBol模型下的价格更接近市场价格。

因场内交易为竞价交易，考虑到实值期权在临近到期日时行权风险上升，所以其买卖价差较大且成交量有限，市场作用接近于期货，此时其成交价格并不能精确体现期权实际价格，而虚值期权相对来说买卖价差更小，且不存在套利空间，所以其价格能较好地反映期权的实际价格。因此考虑计算虚值期权的3种误差，得到结果如表8至表10，可以看出，与Black‐Scholes模型相比，KoBol模型的定价更贴近市场实际价格。

在前文提到了Black‐Scholes模型不能完美地描述实际市场，主要是因为Black‐Scholes 模型假设在市场风险中性下标的资产的预期收益分布服从正态分布，即隐含收益分布与市场不符。这样的不足之处导致了有波动率微笑的存在，所以在利用Black‐Scholes模型进行场外期权定价时，需要根据期权的期限与行权价来调整波动率，从而会产生相应的误差，如果能够将不同行权价期权的隐含波动率控制在更小的范围甚至接近一致，那么对于期权的定价则具有重要意义。

表4 50ETF场内期权两种模型定价Fig. 4 Option prices of 50ETF in two models

表5 300ETF场内期权两种模型定价Tab. 5 Option prices of 300ETF in two models

表6 50ETF场内期权两种模型与市场价格比较Tab. 6 Comparisons of two models with market price of 50ETF options

接下来反演计算隐含波动率微笑曲线，KoBol模型和Black‐Scholes 模型的参数选取依然如表3，考虑到波动率与期权价格的单调关系以及期权的内在价值，利用二分法反推虚值期权的隐含波动率。选取虚值期权，即行权价高于标的价格的看涨期权与行权价低于标的价格的看跌期权数据进行计算后，KoBol 模型和Black‐Scholes 模型下不同行权价对应的虚值期权隐含波动率曲线即为图5，横轴为虚值期权行权价，纵轴为期权的隐含波动率。表11给出了虚值期权在KoBol模型和Black‐Scholes模型下隐含波动率的具体数据。

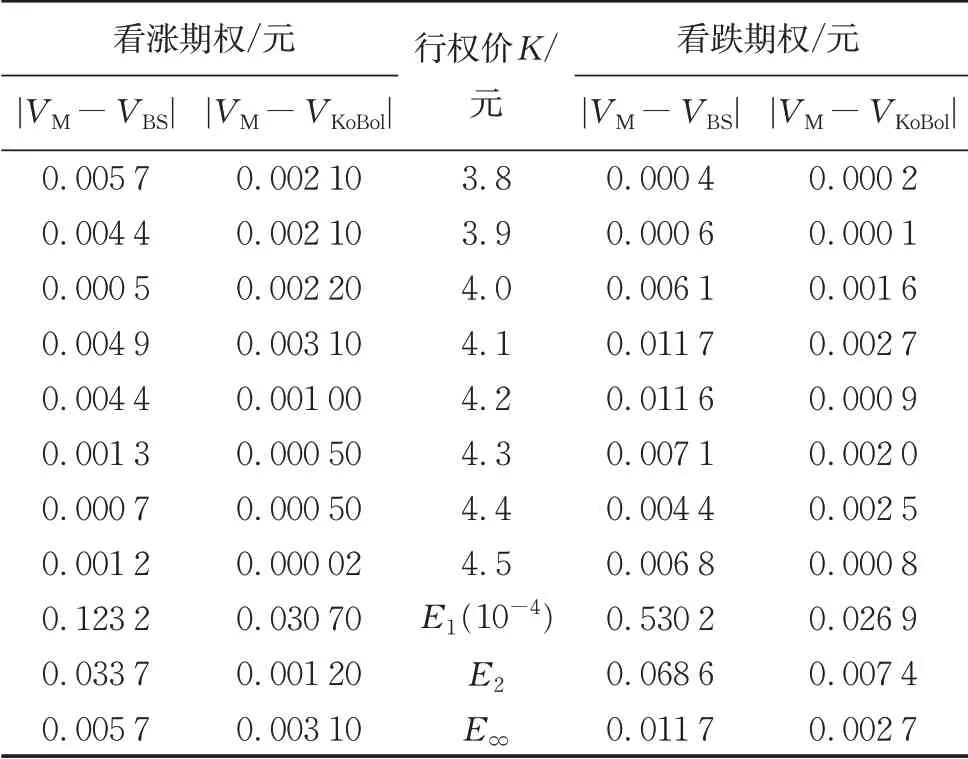
表7 300ETF场内期权两种模型与市场价格比较Tab. 7 Comparisons of two models with market price of 300ETF options

表8 50ETF与300ETF虚值期权的均方误差E1Tab. 8 Error E1 of 50ETF and 300ETF OTM options

表9 50ETF与300ETF虚值期权的相对误差E2Tab. 9 Error E2 of 50ETF and 300ETF OTM options

表10 50ETF与300ETF虚值期权的最大误差E∞Tab. 10 Error E3 of 50ETF and 300ETF OTM options

可以从图5 看出，无论是50ETF 还是300ETF，场内虚值期权的隐含波动率在KoBol模型下被控制在了一个更小的范围内，且波动率曲线更为平稳。由表11 也可以看出，KoBol 模型下的隐含波动率标准差更小。这都说明了KoBol模型在此参数下更好地描述了该时刻标的资产的隐含收益分布。

表11 2020年1月3日股指期权隐含波动率Tab. 11 Implied volatility data of index options on 2020/1/3

图5 2020年1月3日股指期权隐含波动率图Fig. 5 Implied volatility of index options on 2020/1/3

5 结语

本文利用带位移的Grünwald 差分格式对一类基于列维过程的分数阶期权定价模型进行了离散，分析了数值格式的稳定性条件，采用预处理Krylov子空间方法求解对应的线性代数方程组，数值结果验证了模型与算法的有效性。同时，针对国内股指期权的实际交易数据，利用KoBol 分数阶模型对股指期权进行定价并反演计算波动率微笑曲线，通过实证分析说明该模型比Black‐Scholes模型有更好的效果。