Switch Corridor方差互换定价的蒙特卡罗加速算法

马俊美，余 律，贾晓雨

（1. 上海财经大学数学学院，上海200433；2. 上海财经大学上海市金融信息技术研究重点实验室，上海200433；3. 莆田学院 金融数学福建省高校重点实验室，福建莆田351100）

波动率衡量的是标的资产价格的不确定性，是金融风险度量的重要标志。近年来，波动率风险引起金融市场的广泛关注，波动率交易成为风险管理的重要主题。基于VIX（volatility index）指数而衍生的波动率和方差产品是管理市场波动率风险的主要工具，具备重要的长尾系统性风险避险能力，在极端行情中可以提供很好的避险效果，抵御市场的巨幅波动。在2008年金融危机中，波动率衍生产品发挥了比传统风险管理工具更精准和高效的“保险”功能，不仅能有效增强投资组合收益率，同时还能降低收益率的波动率，并在极端情况下提供有效的保护功能。2020年，随着新冠肺炎疫情的全球蔓延，各国股指纷纷大跌，全球经济下行风险急剧增大，分散化投资在系统性风险面前显得不堪一击，而VIX则与传统资产的负相关性进一步提高，如果把波动率衍生品加入到投资组合中，可以起到很好的对冲甚至超额保护的效果。

波动率衍生产品在海外成熟市场已得到投资者广泛认可，不断有相关的衍生产品上市，成交量逐年上升，品种也日益多样化。传统的波动率衍生品是基于一个标的波动率指数而衍生的产品，为对冲一个市场上的波动率风险而设计的。2012 年，由瑞士信贷（Credit Suisse）率先推出了跨市场对冲波动率风险的Switch Corridor方差互换产品，一经推出，该产品成为了结构性产品市场上被广泛交易的一类新型方差产品。Switch Corridor 方差互换是传统的走廊方差互换（Corridor Variance Swap）的自然延伸，不同之处是标的资产的个数，Switch Corridor方差互换的收益取决于两个价格过程：Corridor资产Sc和Variance资产Sv，当Corridor资产在预先定义的范围内时Variance资产的方差才会被累积，Switch Corridor方差互换的收益函数为

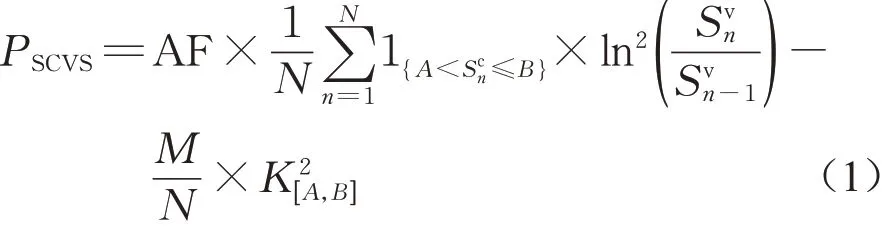
式中：AF表示年化因子（通常为252）；A、B表示Corridor资产价格的上、下限；为敲定方差；N为计算总天数；M是Corridor资产落在价格区间内的总天数，即

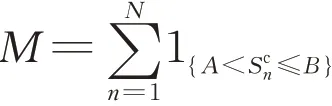
Switch Corridor 方差衍生品是为了满足客户对冲不同市场、不同标的资产的波动率风险需求而推出的新型产品。当一个市场的Corridor 资产落在预先定义的范围内时，另一个市场的Variance 资产的方差才会被累积，Switch Corridor产品能起到对冲跨市场之间的波动率风险的作用，通过该产品的交易，不同的金融市场被联结起来，可以帮助投资者起到更好的管理风险的作用，具有重要的市场地位。

近几年来该产品的交易量一直稳步上升，逐渐成为市场上最受欢迎的新产品系列之一，被称为对冲基金客户和投资银行的双赢产品。从对冲基金客户的角度来看，它允许客户在不同的市场建立盈利头寸。Switch Corridor方差衍生品的主要吸引力在于客户可以在表面的特定部分上交易指数之间波动率的相对溢价/折扣。这为两个不同的波动市场提供了有吸引力的交易机会。在实践中，客户通过做多隐含波动率和实现波动率之间的差异较小的市场的方差（例如亚洲或欧洲指数），同时卖空隐含波动率和实现波动率之间的差异较大的市场的方差（通常是标准普尔500指数SPX）而获利。从投资银行的角度来看，它自然适合银行的风险状况，构成了其结构性产品业务的期权风险要素之一Vega曝露的自然对冲。银行可以通过利用世界上最具流动性的标的来对冲像美国一样更加波动的市场，使得银行可以回收风险并转移/升级流动性。随着走廊差异交换，人们可以在相当具体的市场水平范围内回收Vega风险，这与来自结构性产品服务台的Vega不平衡的概况非常吻合。从风险管理的角度来看，这是一个使经销商能够维持零售业务的关键产品。Switch Corridor方差衍生产品获得“2016年亚洲风险投资年度最佳交易奖”［1］。

在过去的几年里，市场对Switch Corridor方差衍生产品表示了极大的兴趣，然而人们对它的研究程度并没有赶上经销商和对冲基金对这个产品的强烈需求程度。2017年8月，瑞士信贷的亚太地区定量策略主管兼香港股票模拟全球产品负责人Hong，在几何布朗运动框架下，使用Copula法对Switch Corridor方差互换提出一种封闭式解决方案［2］。该方法比原始的Monte Carlo模拟方法快80～120倍，由此Hong获得了“2017亚洲风险大奖”。但是Hong是在几何布朗运动模型下进行定价研究的，他的研究结果不适合求解随机波动率模型下的Switch Corridor 方差衍生产品价格，而随机波动率模型相比几何布朗运动，能够更好刻画金融资产的尖峰厚尾现象，以及波动率的均值回归等特点［3］。基于随机波动率模型计算得到的产品价格同时考虑了资产价格的风险与波动率的风险，能够更为完整彻底地对冲存在的风险源。因此，设计一套既能支持多种随机波动率模型，又能快速处理Switch Corridor方差衍生产品定价的算法具有重要的理论和应用价值。

关于随机波动率模型下Switch Corridor方差产品的定价问题研究的主要难点是维数高，相关性难于处理。这是一个基于四维标的过程的路径依赖型的非线性计算问题，产品的价格满足N个偏微分方程组，每一个偏微分方程是一个四维的非线性方程，大部分情况下无解析解。若用有限差分方法直接对问题进行求解，所需计算量极大，进行计算所需付出代价太大以至无法计算。基于单标的资产的方差互换定价研究中常用的特征函数法［4］、鞍点法［5］等也不易推广应用到二维Switch Corridor方差产品的定价研究中。

本文使用加速蒙特卡罗方法研究Switch Corridor方差产品的定价问题。蒙特卡罗（Monte Carlo）方法是一种以概率统计为基础，通过随机抽样获得数值结果的计算方法。由于其收敛速度和问题维数无关等重要特性，该方法被广泛应用于多标的资产、路径依赖等情形下的定价问题，随着衍生产品的不断创新，其定价的复杂度也在不断增加，蒙特卡罗方法的普遍适用性已然使其成为风险管理和资产定价的基本工具之一。但Monte Carlo方法的主要缺点是收敛速度慢，通常要想提高精度一位有效数字，需要增加100倍的工作量。因而众多学者提出各种方差减小技术来缩减Monte Carlo模拟误差。常见的方差缩减技术有控制变量法、重要抽样法、条件蒙特卡罗法等［6］。其中，控制变量法是目前研究最为广泛的方法之一，其关键在于寻找与原问题高度相关的控制变量。如，Kemna等基于几何平均亚式期权的解析解，以其作为控制变量，对算术平均亚式期权进行了定价［7］；Ma等研究了GARCH（广义自回归条件异方差）模型下的控制变量加速模拟问题［8］；Shin等人使用控制变量技巧研究了LIBOR（伦敦同业拆借利率）市场模型下百慕大互换期权的定价问题［9］。

本文将着重使用控制变量技术，研究高维的Heston 随机波动率模型下Switch Corridor 方差互换的加速模拟定价问题。

1 Monte Carlo方法及控制变量技术

Monte Carlo 方法主要适用于无法求出解析解的数学问题，例如求解复杂随机变量的期望值或某一事件发生的概率。在这里，假设需要估计随机变量X，其期望为μ，方差为σ2。可以根据其概率密度函数生成m 个独立同分布的随机数Xi( i=1，2，…，m )，那么X期望值的蒙特卡罗估计即为

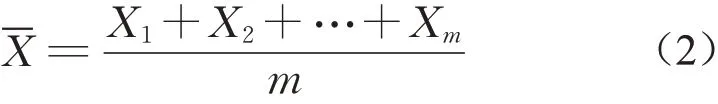
由中心极限定理可知，该估计量的误差为

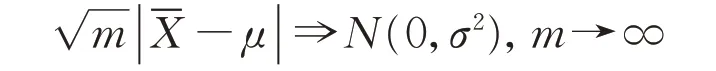
因此可以看到，Monte Carlo 方法是基于简单的概率理论来解决问题，避免了复杂的分析推导，但是它的结果具有随机性，会引入随机模拟误差。可由中心极限定理推出其收敛速度为O( m12)。该速度仅与模拟次数有关，与问题的维数无关。为了提高精确度，模拟次数通常会非常大，这会使得计算效率十分低下。因此，本文引入了控制变量方法。

控制变量方法是一种被广泛应用的蒙特卡罗方差缩减技术，它充分利用了已知量的估计误差从而降低未知量的估计误差［6］。对于式（2）的Monte Carlo模拟，现在假设在每一次对Xi取样的同时计算另一个随机变量Y的随机数Yi，其中( Xi，Yi)独立同分布，且E [Y ]已知。则对于每一个确定的b，可以得到

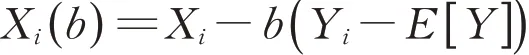
那么随机变量X基于控制变量Y的蒙特卡罗估计即为

由于E [ X (b)]= E [ X ]，即该估计量是无偏的。其方差为

其 中，ρXY为X 和Y 的 相 关 系 数。 显 然 当b*=Cov [ X，Y ] Var [ X ]时，σ2(b*)取得最小值

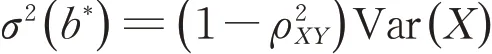
由此可知，控制变量法对误差的减小效果取决于X 和Y 的相关程度，且相关性越高效果越好。因此，本文以简化模型下Switch Corridor 方差互换的价格作为Heston 模型下产品价格的控制变量，保证了高度的相关性。

在实际应用中，若E [Y ]未知，往往σY和ρXY也是未知的，这样就需要估计b*。通常将b*做如下估计，此时仍能得到控制变量法的大部分好处。

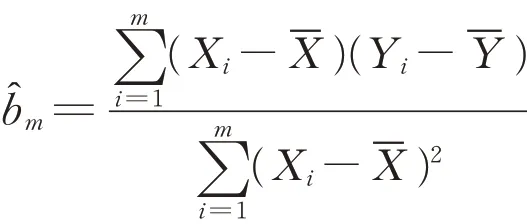
2 高维Heston模型下的产品定价

2.1 随机波动率模型

隐含波动率的微笑现象表明资产服从常数波动率的假设并不符合市场的普遍规律。在随机波动率模型中，Heston 模型逐渐被认为是较为合适的模型之一［10］。因此，本文研究了Variance资产及Corridor资产均满足Heston 波动率模型的情形下，Switch Corridor 方差互换产品的定价问题。假设两标的资产分别满足如下相关的扩散过程：

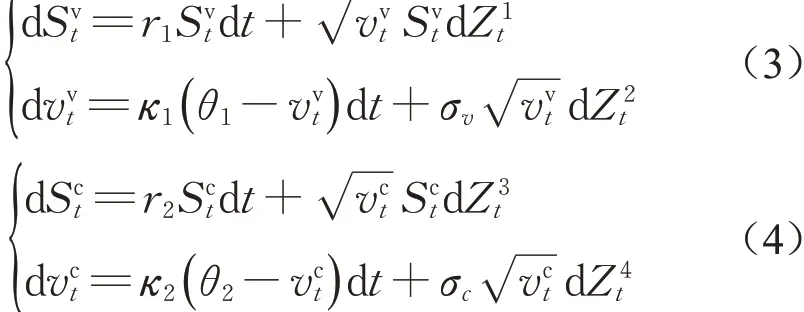
其 中 ， E [ dZ1tdZ2t]= ρ1dt，E [ dZ3tdZ4t]=ρ2dt，E [ dZ1tdZ3t]= ρdt；vvt表示Variance 资产的方差过程，σv为其波动率，当t趋于无穷时，vvt的期望值以回复速度κv趋近于θv；同理，vct表示Corridor 资产的瞬时方差，遵循回复速度为κc，长期均值为θc的均值回复过程。均值回复过程保证了资产的波动率受到一定的限制，不会出现极端值的情况。本文使用控制变量Monte Carlo加速技术研究了在模型（3）和（4）下，收益函数为（1）的Switch Corridor 方差互换产品的定价问题。

2.2 基于仿射扩散过程的控制变量解析解

考虑简化模型下，Switch Corridor方差互换产品的定价求解问题，以获得原问题高效的控制变量。构造如下辅助过程：假设Variance资产和Corridor资产过程均服从波动率为关于时间t的函数的几何布朗运动

为方便讨论，记为向量形式

定义1 令Σ(x) = σ( x )σ( x )T，式（7）表示的过程为d 维仿射扩散过程，当且仅当漂移项μ(x)和扩散项Σ(x)有如下形式：

其中：αi( i= 1，2，…，d )；a 为d 维常数矩阵；βi( i=1，2，…，d )；b为d维常数列向量。

由于基于函数波动率的二维几何布朗运动的μ与Σ 均不包含随机变量，因此符合仿射扩散过程的定义。d维仿射扩散过程的主要性质如下。

性质1 记iRd={ iu|u∈Rd}，若Xt为d 维仿射扩散过程，则存在关于t 连续可微的函数ϕ(t，u)：R+×iRd→C，ψi(t，u)：R+×iRd→Cd，i=1，2，…，d，对于任意的u∈Rd，t ≤T，过程Xt均满足

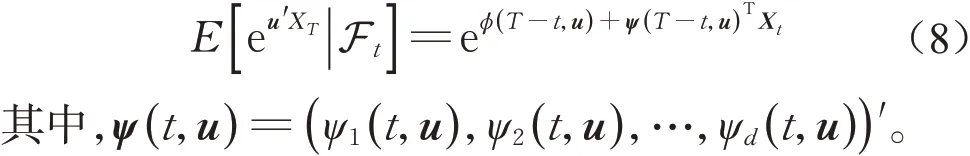
性质2 若Xt为d 维仿射扩散过程，则ϕ(t，u)与ψ(t，u)满足如下Riccati微分方程组：

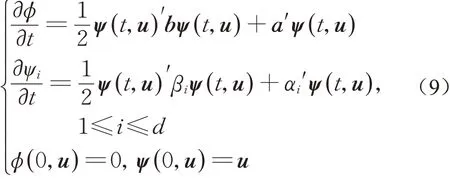
反之，若Riccati 方程组（9）存在唯一解，使得对于任意的0< t ≤T，ϕ(t，u)+ ψ(t，u)'x 具有非负实部，则Xt是仿射扩散过程。

性质1 和性质2 的证明可参见文献［11］。有关仿射扩散过程的更多性质及应用可参考文献［12］。由此可以直接计算得到该二维几何布朗运动的漂移系数及扩散系数分别为

设u=( u1，u2)'，与上述系数一同代入式（9）解得

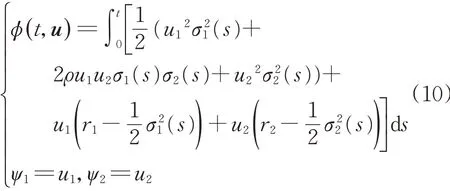
定理1 基于标的过程式（5）、（6）且具有收益函数（1）的Switch Corridor方差互换产品的价格为

证明 由于具有上、下界的示性函数可由两个上界示性函数相减得到，因此先考虑Corridor 资产的价格范围仅包含上界的情况。Switch Corridor 方差互换的收益公式（1）由前、后两部分组成。先考虑减号前的部分，对于t ∈(tn−1，tn)，n= 1，2，…，N，假设Corridor资产上限为ex，需要求的期望即为

由反演定理，可以利用逆傅里叶变换得到原示性函数的半解析表达式

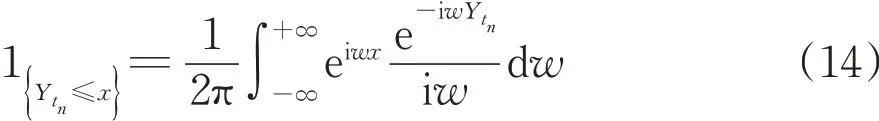
将式（13）及（14）代回式（12），利用重期望公式，由性质1及性质2，可以得到

式中：u1=(u1，−iw)'，u2= (0，−iw)'；ϕ(t，u) 的具体形式如式（10）所示。

对于减号后的部分，同理先考虑如下形式：

将Corridor资产上、下界的ln值分别代入x后相减，并代回求期望后的收益函数（1），可以得到定理1中的公式（11）。

特别地，当σ1(t )和σ2(t )为常数波动率时，Switch Corridor方差互换的价格有更简洁的解析表达

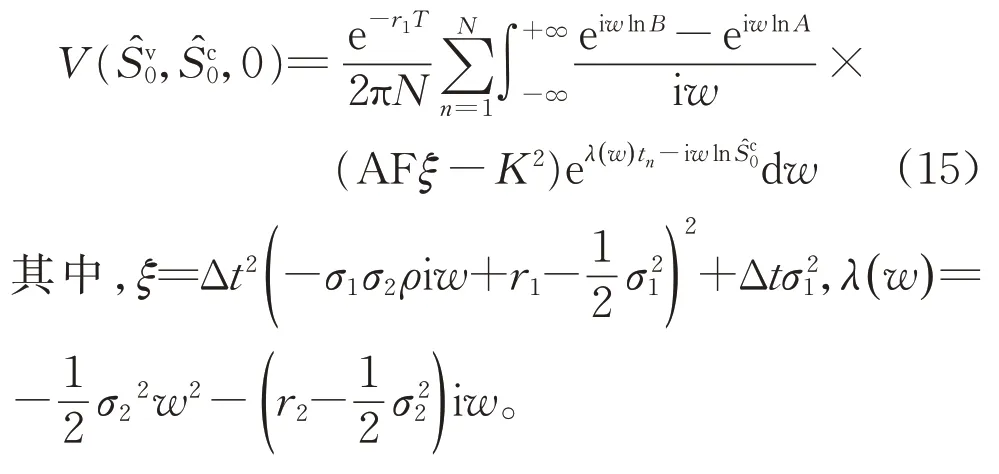
2.3 控制变量波动率的选取

控制变量方差缩减技术的效果取决于所选控制与原问题的相关性，因此控制变量波动率的选取也是至关重要的。需要选择最具有代表性的σ1(t )和σ2(t )使得控制变量与原问题之间有较高的相关性，从而达到较好的方差减小效果。本文选取控制变量的标的过程（5）和（6）中的波动率函数σ1(t )和σ2(t )为随机波动率过程（3）和（4）的数学期望。

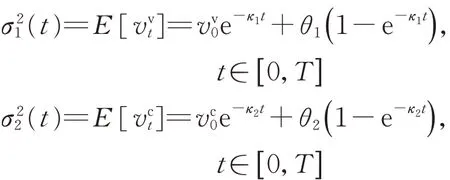
本文进一步将该控制变量的加速效果与静态波动率常数及按Xu 等［13］提出的方法选取分段波动率常数所对应的控制变量的加速效果进行比较。Xu等讨论了当原问题为基于任意随机波动率模型时的一类广义选取方法，假设原问题中的资产服从如下广义随机波动率模型：

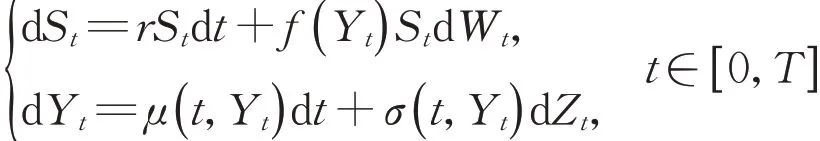
式中：f (Y )、μ(t，Y )、σ(t，Y )都是已知的函数；Wt和Zt是相关系数为ρ的布朗运动。同样地构建一个作为控制变量的虚拟标的资产，假设其满足

他们将问题转化为如何找到合适的目标函数以表示St与Ŝt的近似相等，并求解最优的σ̂t。考虑到求解的可行性与复杂性，他们选择了如下优化目标：

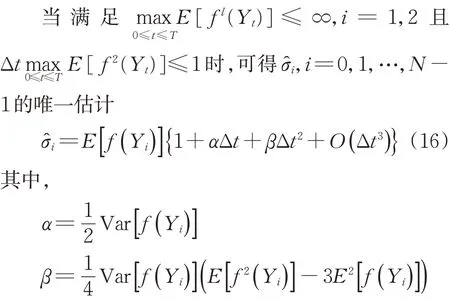
在实际运用中，对于适当的Δt与模拟次数m，式（16）可近似为

为方便后文中的描述，将上述3 种辅助标的过程的波动率选取方法分别命名为动态波动率选取法、静态波动率选取法以及广义波动率选取法。

3 数值结果及分析

以2. 2 节推导出的Switch Corridor 方差互换价格的解析解作为控制变量，分别应用动态函数波动率、静态常数波动率以及广义分段常数波动率3 种波动率选取方法，对高维Heston 波动率模型下的该产品进行蒙特卡罗模拟。

3.1 结果对比

参数设置：敲定方差K= 0.01，年化因子AF=252，N= 100，T= 1，Corridor 资产价格的下限A=9，上限B= 11；Variance 资产的方差初值vv0= 0.62，长期均值θ1= 0.25，回复速度κ1= 2，方差波动率σv= 0.01，相关系数ρ1= 0.2，所在市场无风险利率r1= 0.05；Corridor 资产的方差初值vc0= 0.62，长期均值θ2= 0.25，回归速度κ2= 2，方差波动率σc=0.01，相关系数ρ2= 0.2，所在市场无风险利率r2=0.05；资产间相关系数ρ= 0。分别使用了2. 3 节中介绍的3 种控制变量波动率的选取方法进行了Monte Carlo 模拟。Monte Carlo 模拟的结果见表1所示。

表1 基于3种波动率选取法的控制变量蒙特卡罗模拟Tab. 1 Control variate method of Monte Carlo simulation results based on three volatilities of GBM

表1中，M表示模拟路径数；P1表示传统蒙特卡罗模拟得到的Switch Corridor 方差互换价格；P2、P3、P4分别表示基于静态、动态及广义波动率选取的控制变量下Switch Corridor 方差互换的蒙特卡罗模拟价格；Ei，i= 1，2，3，4 表示各方法对应的模拟误差；为了更好地比较3 种波动率选取算法的优劣，VRi和VTRi的定义为

分别表示各方法对应的方差减小倍数及考虑时间比的综合减小倍数。

由表1可以看到，除静态方法以外，其他方法的方差减小倍数都在300 倍以上，综合减小倍数均在200倍以上，说明使用函数波动率或分段常数波动率的几何布朗运动下该产品的解析解作为控制变量有着较为明显的方差缩减效果，且随着模拟次数的增加，方差减小效果及综合减小效果均越好，计算得到的产品价格也越稳定。还可以发现，对于该产品而言，动态的选取方法相对于广义选取法有着更好的表现，且当路径数达到20 000时，该选取法甚至可以有高达459. 19倍的缩减效果，这大大提高了计算精度。若要使原始蒙特卡罗模拟达到同样的精度，模拟路径数需增加VR2倍。

另外，单独考察了基于动态波动率的控制变量与原问题的相关性。图1为两个模型下方差互换价格的散点图。其中，纵坐标表示基于函数波动率的几何布朗运动下Switch Corridor 方差互换的价格，即控制变量的价格；横坐标表示双Heston 随机波动率模型下该产品的模拟值。

图1 两类方差互换的价格散点图Fig. 1 Scatter plots of values of two types of variance swaps

图1 中的散点可近似为一条过原点的直线，即控制变量与原问题之间呈现正比例的关系。进一步地，可以根据样本数据估计得到两者间的相关系数为ρ= 0.999 1，可以看到控制变量与原问题有高度的相关性。由控制变量的原理可知，基于该控制变量的蒙特卡罗模拟可以达到较好的方差缩减效果，大大提高了计算的精确度。

除此之外，还考虑了其他参数对方差减小效果的影响。保持其余参数不变，仅改变Corridor 资产或Variance资产方差过程的初值，在动态选取法下，可以得到如表2中的结果。

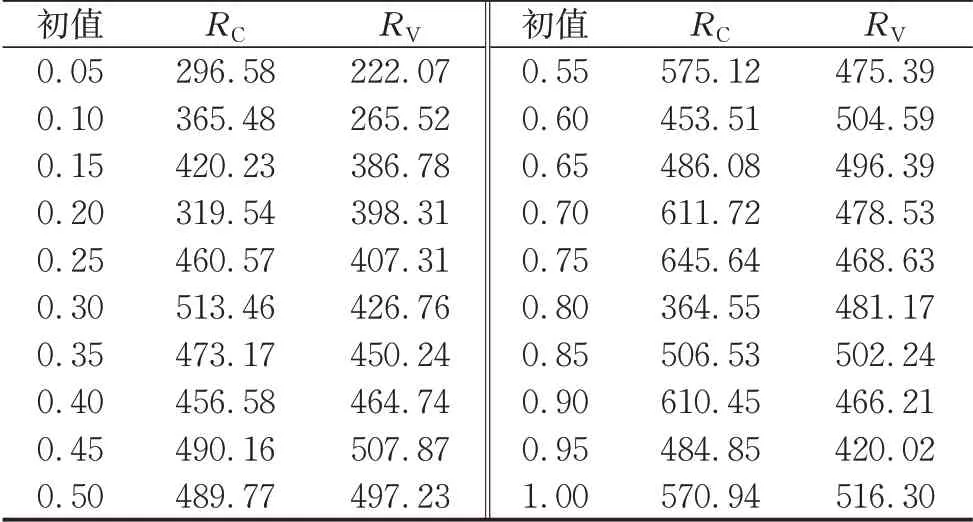
表2 动态选取法下资产方差初值对加速效果的影响Tab. 2 Effect of initial volatility in the dynamic method

表2 中，RC表示动态选取法下当保持其他所有参数不变而仅改变Corridor 资产的方差初值时得到的缩减倍数；RV表示动态选取法下当保持其余参数不变而仅改变Variance资产的方差初值时得到的缩减倍数。图2 记录了随着Corridor 资产及Variance资产方差初值的变化动态选取法下方差缩减倍数的波动。

图2 动态选取法下方差初值对加速效果的影响Fig. 2 Effect of initial volatility in the dynamic method

由图2可以看出，当保持其他参数不变时，方差缩减倍数并不是随着这两类资产方差初值的增大线性增加，而是处于波动上升的状态。当初值较小时，图中实线及虚线均呈现上升的趋势，且实线始终处于虚线的上方，说明此时在动态选取法下适当增加两标的资产方差的初值均可以提高精确度，且Corridor 资产方差初值的改变有着更好的方差减小表现。明显可以看到，虚线的整体波动范围较实线而言更小，实线的波动幅度更大，这说明Variance资产方差初值的改变对方差缩减倍数的影响效果更小。对于最优值的确定有待进一步的讨论分析。

3.2 模型参数对产品价格的影响分析

进一步地，考察了Switch Corridor 方差互换的价格与两个标的资产模型参数之间的关系：无风险利率r、长期均值θ、回复速度κ、方差初值v0及相关系数ρ1、ρ2、ρ，如图3所示。

由3a 可以看到，随着Corridor 资产所在金融市场无风险利率的增加，产品价格会有小幅度的波动上升；然而对于Variance资产无风险利率的改变，产品价格基本维持在0. 165 附近，没有明显的增加。在图3b 中，Corridor 资产的长期均值增加会导致产品价格小幅下降；而Variance 资产长期均值的增加会导致产品价格较大幅度的上升；在图3c 中，随着Corridor资产的回归速度的增加，产品的价格以一个非常小的幅度波动增加；而Variance 资产的回复速率的增加则会导致产品价格缓慢递减；在图3d 中，产品价格与Corridor 资产的方差初值呈现出负相关的趋势；而与Variance 资产的波动率初值大致成正比例关系，且幅度相对较大；由3e和3f可知，产品价格受资产相关系数影响较小，没有明显的趋势。

总体而言，标的资产的长期均值θ以及方差初值v0对Switch Corridor 方差互换产品价格的影响程度更大；除无风险利率及相关系数之外，Corridor 资产对价格的影响大多呈现负相关，而Variance 资产对产品价格的影响大多呈现正相关，且Variance 资产参数变动对产品价格的影响程度要高于Corridor资产。这些特征与Switch Corridor 方差互换的收益函数是相吻合的。

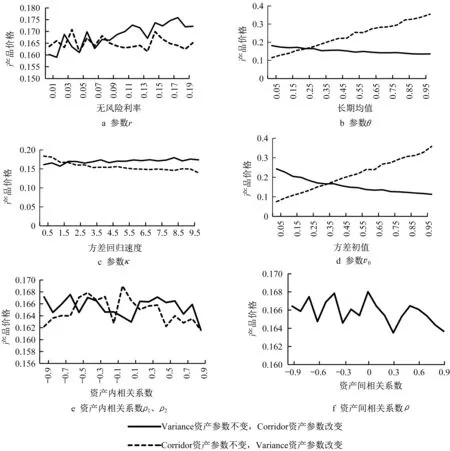
图3 模型参数对产品价格的影响Fig. 3 Price of product against parameters

4 结语

本文首先基于仿射扩散模型的性质推导出了函数波动率的几何布朗运动模型下Switch Corridor 方差互换价格的解析解，以此作为控制变量对高维Heston 模型下的该产品的模拟定价进行加速，并采用了3种布朗运动波动率的选取方法进行了对比分析，同时考察了影响方差互换产品价格的因素。结果表明对于该产品而言，基于动态波动率的该控制变量是极其有效的，大大减小了蒙特卡罗的模拟误差，提高了计算效率，为其他随机波动率模型下Outperformance Corridor Variance Swap 等同类多标的资产的方差互换产品的定价研究提供思路。

作者贡献申明：

马俊美：总体研究方向的确定，文章的撰写。

余 律：GBM下产品解析解的推导，文章的撰写。

贾晓雨：程序的实现。