永磁同步电动机随机系统有限时间模糊自适应反步控制

宋思佳，刘加朋，于金鹏，程 帅

(青岛大学 自动化学院，山东 青岛266071)

0 引 言

永磁同步电动机(PMSM)凭借其结构简单、效率高、使用寿命长和实用性强等优点已经广泛应用在农业和工业等领域。因PMSM高度非线性、强耦合以及多变量，在实际运用中易受到外部负载扰动、电机参数变化等不确定因素的影响，为更好实现PMSM的位置跟踪控制，需要研究有效的控制策略。近年来，相关研究者针对PMSM非线性系统已经研究了许多有效控制策略，例如滑模控制[1]、直接转矩控制[2]、鲁棒控制[3--4]和反步控制[5-7]等。

但是传统反步方法并没有考虑实际运行中的随机扰动问题，例如：阻尼转矩和磁饱和等可能会引起电动机自感互感、转矩等相关参数发生变化。因此本文使用模糊自适应控制方法处理电机模型中随机非线性函数。

近年来，有限时间方法的应用受到广泛关注。Bernstein[8-9]首先提出了有限时间基于Lyapunov的非线性系统稳定性理论。相比于传统控制方法有限时间方法具有许多优点，例如：缩短动态响应时间、收敛迅速、控制精度高和抗干扰能力强。

基于上述问题，本文针对PMSM随机非线性系统提出了一种基于有限时间的控制方法。本文提出的有限时间模糊反步位置跟踪控制与传统方法相比，主要优点在于(1)考虑了PMSM系统运行过程中的随机干扰，使用模糊逻辑控制处理了电机模型中随机非线性函数，简化了系统的控制器结构。(2)将有限时间控制方法运用在PMSM随机系统当中，提高了系统的收敛、控制精度和抗干扰能力。

1 同步电动机模型

在同步旋转坐标(d-q)下，根据文献[7]PMSM系统的模型可表示为:

(1)

式中,ud,uq表示d，q轴定子电压；id,iq表示电流；ω为转子角速度；θ为转子角度；J为转动惯量；np为极对数;B为摩擦系数；Ld和Lq为d-q坐标系下的定子电感，Rs为定子电阻；TL为负载转矩；Φ为永磁体产生的磁链。为让电机模型能更简便的表示出，新变量定义如下：

(2)

引理1[13]：随机系统可表示为

dx=f(x)dt+h(x)dw

(3)

式中,x∈Rn是系统状态变量，w为独立随机增量过程，f(·):Rn→Rn和h(·):Rn→Rn×r是在x上的局部Lipschitz函数且f(0)=0和h(0)=0。对于V=V(x)∈C2，C2表示复数集，定义差分运算,由微分法则可知：

(4)

考虑到随机扰动的问题，PMSM的模型表示为：

(5)

其中，ψ1、ψ2、ψ3、ψ4表示未知平滑的非线性函数。

引理2[15]：对于随机系统，假设f(0)和h(0)在t上是一致有界的，如果V=V(x)∈C2，a0>0，0<β<1，b0>0.

μ1(x)≤V(x)≤μ2(x)

(6)

对于∀x∈Rn，t>t0，随机非线性系统都是半全局实际有限时间稳定。

2 永磁同步电动机模型的有限时间模糊自适应反步控制器设计

定义系统误差变量如下：

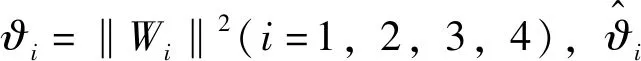
(7)

其中‖Wi‖为向量Wi的范数，已知li、hi和εi为正设计参数，i=1,2,3,4.

Step 1：选取第一个子系统Lyapunov 控制函数

(8)

对式(8)求导，可得

(9)

由杨氏不等式得

(10)

(11)

选取虚拟控制函数和自适应律为

(12)

其中r1,m1为正数，根据式(11)和 式(12)得

(13)

Step 2:选取Lyapunov 控制函数

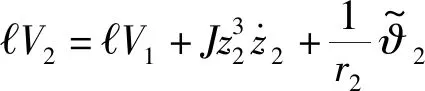
(14)

TL具有不确定性，存在d>0满足|TL|≤d，由杨氏不等式得

(15)

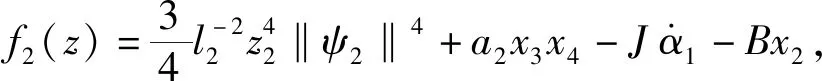
取虚拟控制函数和自适应律

(17)

其中r2,m2为正数，根据式(16)和 式(17)得

(18)

Step 3：选取Lyapunov 控制函数

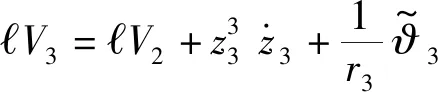
(19)

由杨氏不等式得

(20)

取虚拟控制函数和自适应律

(22)

其中r3,m3为正数，根据式(21)和 式(22)得

(23)

(24)

由杨氏不等式得

(25)

(26)

取虚拟控制函数和自适应律

(27)

其中r4,m4为正数，根据式(26)和(27)得

(28)

3 稳定性分析

选取系统的Lyapunov 控制函数V=V4对其求导得

(29)

(30)

i=1,2,3,4.

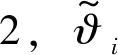
4 系统仿真实验及结果分析

4.1 仿真实验参数设定

为验证上述控制方法，采用Matlab软件仿真实验分析，电动机参数为：

B=0.001158 Nm/(rad/s),J=0.002 kg·m2,

Ld=0.00977H,Lq=0.00977H,Φ=0.1245H,

Rs=0.68 Ω,np=3.

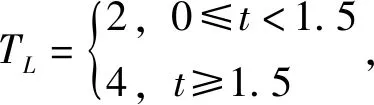
k1=k2=k3=1000,k4=2000,h3=1,

h1=h2=h4=2,r1=r3=r4=100,r2=1540.

4.2 仿真实验结果分析

仿真结果如图1至图4所示，图1(a)至图4(a)是使用有限时间方法，图1(b)至图4(b)是文献[7]中的传统反步法。

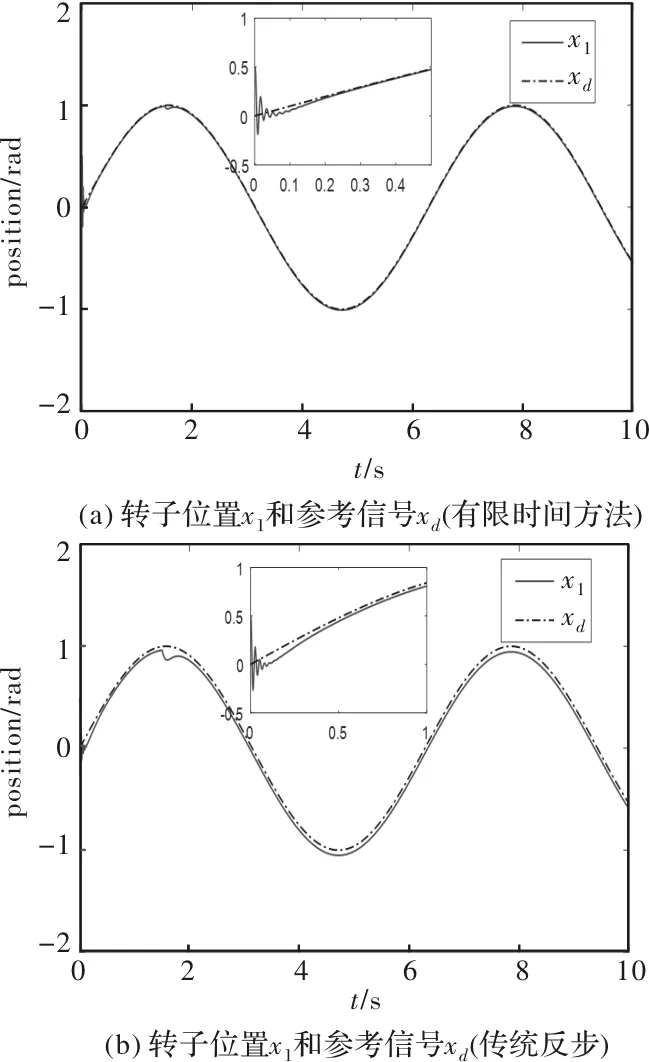
图1 转子位置和参考信号

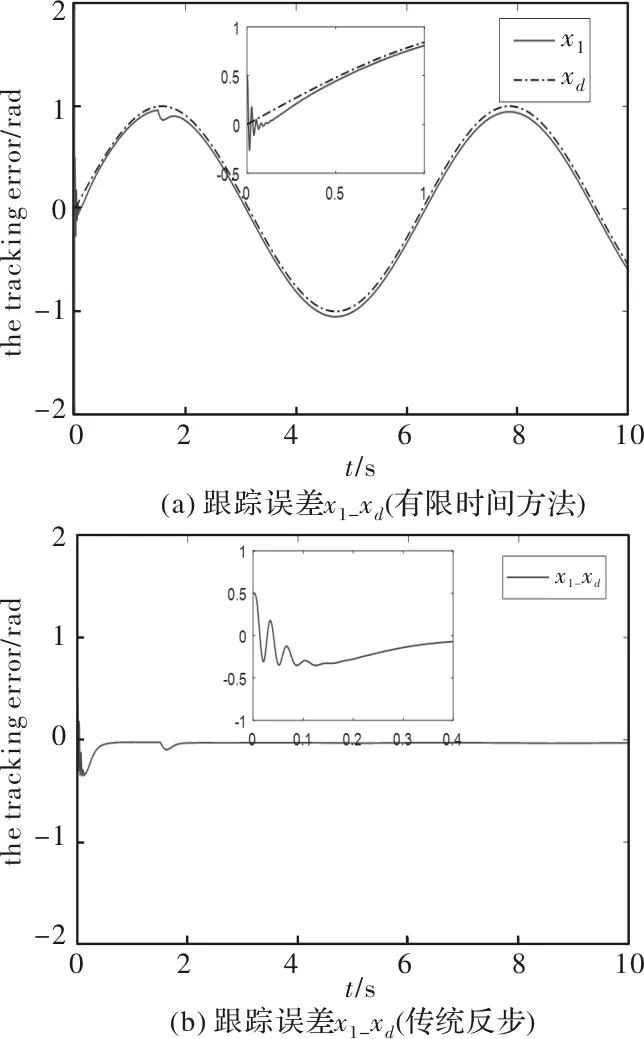
图2 跟踪误差

图3 系统输入uq的轨迹

图4 系统输入ud的轨迹

相比于文献[7]中的传统反步法，加入有限时间控制方法后，系统的收敛速度更快，跟踪效果更好，抗干扰能力更强。

5 结 语

对于存在随机扰动问题的永磁同步电动机，本文结合有限时间控制方法和自适应模糊反步法，设计了一种基于有限时间控制的位置跟踪控制器，实现了PMSM随机非线性控制。仿真结果验证本文所述控制方法能有效的跟踪预期的位置信号。