超声波电机广义最小方差迭代学习转速控制

黄文文，宋 璐，史敬灼

(河南科技大学 电气工程学院，河南 洛阳 471023)

0 引 言

传统迭代学习控制应对时变扰动的能力较差，在受到干扰作用时，传统迭代学习控制不能立即做出相应变化，需等到下次迭代才能对干扰影响做出反应。由此，可考虑将迭代学习与反馈控制相结合[1-3]，以提高迭代学习应对扰动的能力，得到更好的控制性能。

最小方差控制考虑扰动对系统性能的影响，基于对未来时刻输出的预测，按照预测方差最小的原则设计最优控制律，是一种典型的自适应控制算法。不过，最小方差控制不适用于非最小相位系统，且对控制量无约束，可能导致过快的响应速度而影响系统的稳定性。针对这些问题，提出了在目标函数中引入加权多项式和控制量约束的广义最小方差自校正控制，它通过调整加权多项式可得到良好的控制性能[4]。本文将广义最小方差控制与迭代学习控制相结合，构造一种包含预测与闭环控制机制的迭代学习控制策略，用于超声波电机转速控制。

通过设计包含前次控制过程信息的2D优化目标函数和迭代控制律，利用广义最小方差自校正控制方法来设计更新律，得到广义最小方差迭代学习控制律，使其兼顾时间轴的控制性能和迭代轴的学习收敛性能，并具有良好的应对实时扰动的能力。仿真和实验表明，所提控制策略及其设计方法有效，超声波电机转速响应表现出渐进的学习收敛过程，控制效果良好。

1 广义最小方差迭代学习控制策略

设被控对象可用如下自回归滑动平均模型描述

A(z-1)yk(i)=z-dB(z-1)uk(i)+C(z-1)ξk(i)

(1)

其中

A(z-1)=1+a1z-1+a2z-2+…+anaz-na
B(z-1)=b0+b1z-1+b2z-2+…+bnbz-nb
C(z-1)=1+c1z-1+c2z-2+…+cncz-nc

(2)

d≥1，为纯延时；yk(i)和uk(i)分别为第k次迭代控制过程中i时刻的输出量和输入量；ξk(i)为白噪声。

针对模型式(1)描述的重复过程，给出如下形式的迭代学习控制律

uk(i)=uk-1(i)+lk(i)

(3)

式中，lk(i)为迭代更新律。

将控制律式(3)代入模型(1)得

A(z-1)yk(i)=z-dB(z-1)(uk-1(i)+lk(i))+C(z-1)ξk(i)

(4)

设计如下控制目标函数

J=-E{[P(z-1)(yk(i+d)-yr(i))]2+
[Q(z-1)uk(i)]2+
[S(z-1)lk(i)]2}

(5)

式中，yr(i)为i时刻期望输出；yk(i+d)为第i+d时刻的输出；P(z-1)、Q(z-1)和S(z-1)分别为目标函数中各项的加权多项式，反映控制性能需求，且有

P(z-1)=1+p1z-1+p2z-2+…+pnpz-np
Q(z-1)=q0+q1z-1+q2z-2+…+qnqz-nq
S(z-1)=s0+s1z-1+s2z-2+…+snsz-ns

(6)

式中，阶次np、nq和ns由实际需要确定。需指出的是，与广义最小方差自校正控制策略通常采用的目标函数不同，式(5)所示目标函数增加了lk(i)项以包含前次控制过程信息，使广义最小方差自校正控制与迭代学习控制方法有机融合。

下面推导最优预测模型，以给出未来时刻的输出预测值，用于计算目标函数。引入以下Diophantine方程

C(z-1)=A(z-1)E(z-1)+z-dG(z-1)

(7)

F(z-1)=B(z-1)E(z-1)

(8)

其中

E(z-1)=1+e1z-1+e2z-2+…+enez-ne(ne=d-1)

G(z-1)=g0+g1z-1+g2z-2+…+gngz-ng(ng=na-1)

F(z-1)=f0+f1z-1+f2z-2+…+fnfz-nf(nf=nb+d-1)

采用与广义最小方差相同的方法推导最优预测模型，所得最优预测模型为

(9)

系统输出为

(10)

由式(9)和Q(z-1)的表达式可得

(11)

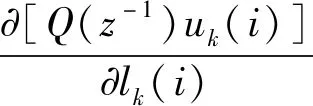
(12)

将式(10)代入式(5)，取其对lk(i)的偏微分，结合式(11)和式(12)，并令其为0，可得

(13)

由式(13)可得使目标函数取极小值的最优控制律为

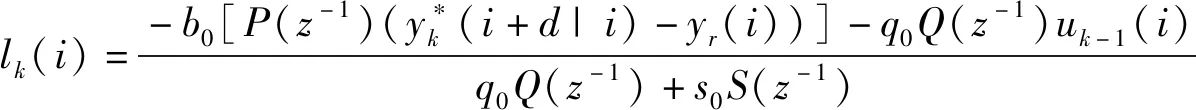
(14)

则广义最小方差迭代学习控制律为

(15)

在广义最小方差迭代学习控制律的设计过程中，需根据控制性能指标要求，选定式(5)中的权值矩阵P、Q、S，随后计算给出式(15)所示的广义最小方差迭代学习控制律。

2 超声波电机广义最小方差迭代学习转速控制器设计

以Shinsei USR60两相行波超声波电机为控制对象，采用文献[5]所建超声波电机系统Hammerstein模型进行控制器设计与仿真分析。对模型中的非线性静态环节求逆，并将其作为超声波电机转速控制器的一部分，与ILC相串联。它与超声波电机非线性环节相抵消，实现非线性补偿，ILC控制器作用于补偿后的、主要特性呈线性的超声波电机。因此，采用仿真分析方法进行控制器设计时，仅考虑超声波电机系统Hammerstein模型的线性动态环节，写为式(1)形式可得

A(z-1)=-1-0.9416z-1+0.0623z-2+0.0471z-3-

0.0255z-4

B(z-1)=0.8218-0.6928z-1

(16)

另外，na=4、nb=1、d=1。取C(z-1)=1，则

E(z-1)=1,F(z-1)=f0+f1z-1
G(z-1)=g0+g1z-1+g2z-2+g3z-3

(17)

根据式(7)可得

G(z-1)=-z(1-A(z-1))=
0.9416-0.0623z-1-0.0471z-2+0.0255z-3

(18)

根据式(8)可得

F(z-1)=B(z-1)=0.8218-0.6928z-1

(19)

则有

(20)

式(20)用来计算预测输出量。将控制律式(15)用作超声波电机转速控制器，尝试选取不同的P、Q、S取值，进行迭代学习控制仿真。根据仿真所得转速阶跃响应性能，确定合适的P、Q和S值。

取Q(z-1)=q0+q1z-1，式(15)成为

(21)

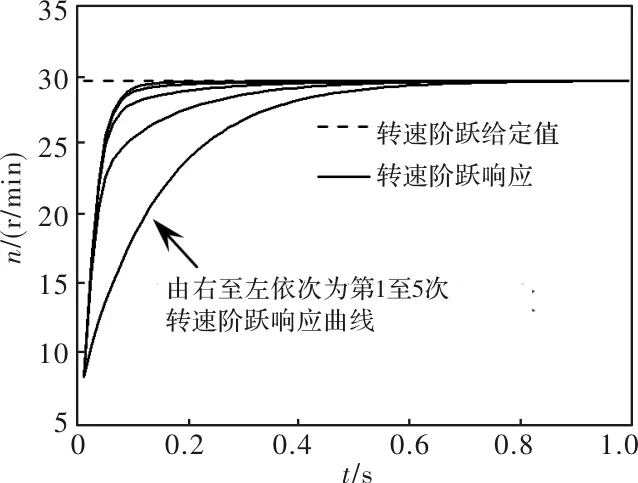
图1 转速阶跃响应曲线(P=[1,0.8],Q=[2,-2],S=0.8)

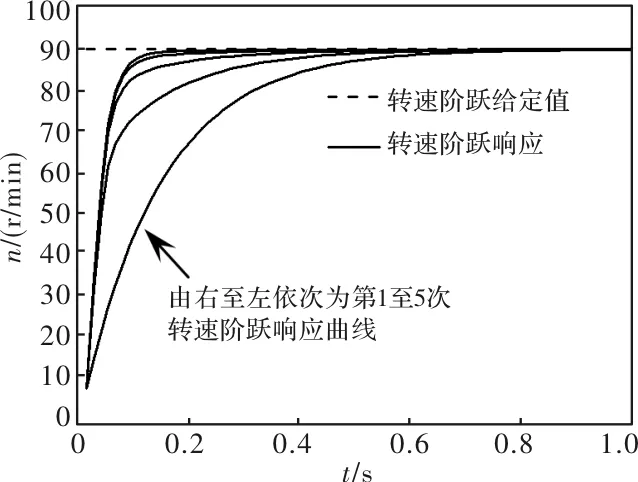
图2 转速阶跃响应曲线(P=[1,0.8],Q=[2,-2],S=0.8)

3 超声波电机广义最小方差迭代学习转速控制实验研究

对上述设计的超声波电机广义最小方差迭代学习转速控制策略进行实验研究，将转速阶跃给定值设定为30 r/min，控制参数与前述仿真设计所得参数相同，进行迭代学习转速控制实验，得实验结果如图3所示。由图3可知，转速阶跃响应曲线逐渐趋于给定值，出现小幅度超调。在前五次迭代中，随着迭代学习的进行，调节时间持续减小，从0.2227 s减为0.0262 s，减小幅度为88.24%，第六次迭代因出现超调使得调节时间略有增大。

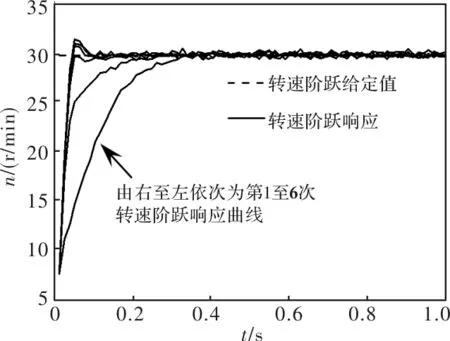
图3 转速阶跃响应曲线(实测, 30 r/min)

将转速阶跃给定值改为90 r/min，控制参数不变，得实验结果如图4所示，转速阶跃响应曲线仍然逐渐趋于给定值，无超调，且随着迭代的进行，调节时间持续减小，从0.3144 s减为0.0524 s，减小幅度为83.33%，表明所提迭代学习控制策略适用于不同转速，且不同转速情况下的控制性能接近。表1给出了两种转速给定值情况下的迭代学习控制性能指标数据。将图3、图4与图1、图2对比，仿真与实验结果接近。上述结果表明所述迭代学习控制策略是有效的，结合仿真进行的控制参数设计方法也是有效的。

表1 两种转速给定值情况下迭代学习控制性能指标(实验结果)

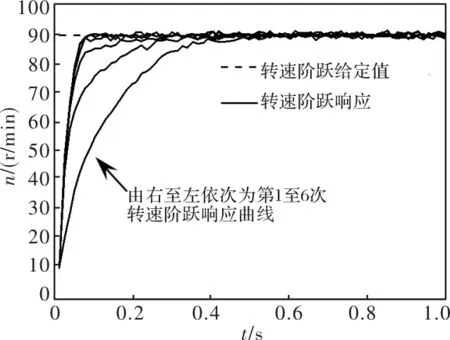
图4 转速阶跃响应曲线(实测, 90 r/min)

进行间歇加载实验，控制参数不变，得到转速阶跃响应如图5所示。可以看出，图5加载情况下，为应对突加负载扰动，控制量在第2、4次迭代有所增加，但增量较小、不足以提供应对突加负载所需要的控制量，使第2次和第4次迭代控制过程出现稳态误差。图6给出了与图5对应的控制量变化曲线，相比于第1次的空载情况，第3和5次的控制量有所增加，使得稳态转速值均略超出给定值；但随着迭代的进行，控制量逐渐减小，在第6次控制量已经减小至与第1次基本一致，转速稳态值重新趋于给定值。

图5 转速阶跃响应曲线(实测, 第2、4次阶跃响应负载0.2 Nm)

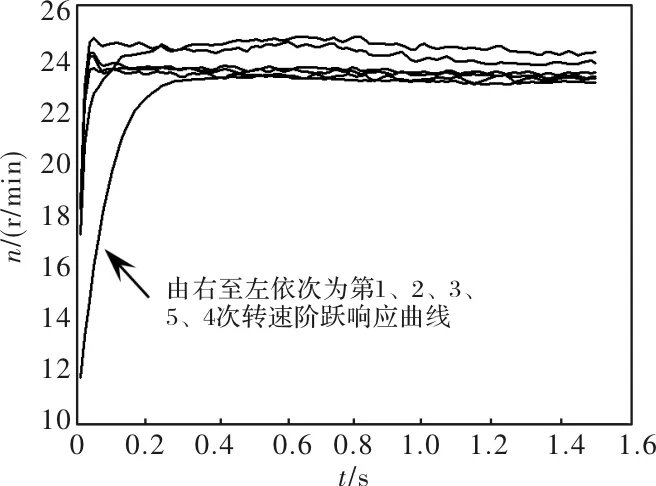
图6 控制量变化曲线(实测, 30 r/min)

以上结果表明，在此控制律作用下，控制器对突加的负载扰动虽能立即做出响应，但因为迭代学习过程对过往控制信息的记忆，延迟了控制量的变化；另外，由负载切换为空载时，例如第5次控制过程，也是因为迭代学习是从前次记忆中学习，前一次控制量的增加使得突然切换为空载后的控制量大于实际需求，稳态转速超过给定值。但随着迭代的进行，控制器能够快速应对稳态误差，第6次控制响应的稳态误差已经为0。

为考察不同负载转矩情况下的控制效果，图7给出了转速给定值为90 r/min、第2、4次加载0.1 Nm情况下的实验结果，转速阶跃响应无稳态误差，性能指标与空载的图4情况接近。上述实验结果表明所述控制律对非重复性的负载扰动具有一定适应能力。

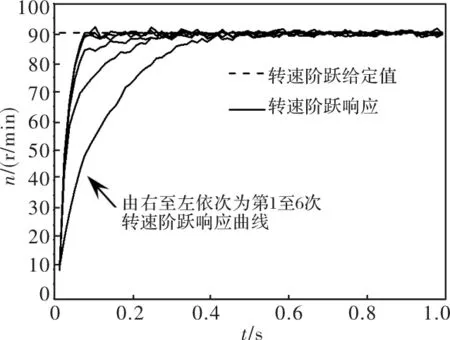
图7 转速阶跃响应曲线(实测，第2、4次阶跃响应负载0.1 Nm)

4 结 语

本文将迭代学习控制与广义最小方差自校正控制相结合，给出了一种超声波电机广义最小方差迭代学习转速控制策略。通过设计迭代控制律，并在目标函数中引入相应的迭代控制项，将迭代学习与广义最小方差控制有机结合，构造广义最小方差迭代学习控制律，使其同时具有沿迭代轴的学习收敛性和沿时间轴的控制稳定性。仿真和实验结果表明，通过调整目标函数中的各加权系数值，可获得良好的电机转速控制性能，且对负载突变等非重复性扰动具有一定的适应能力。