城市路况下电动汽车驱动器最优开关频率选择探讨

杨中哲，王恩隆，杨 欢

(浙江大学 电气工程学院，杭州 310027)

0 引 言

在石油资源逐渐缺乏和环境污染问题日趋严重的社会背景下，新能源汽车行业越来越被人重视[1]。而电池续航能力作为电动汽车最重要的技术指标之一，对其考核的常用标准有美国、欧盟和日本循环工况。其中欧洲的循环工况NEDC(New European Driving Cycle, NEDC)由4个城市路况循环和1个郊区路况循环组成，其中城市路况循环全长4.052 km，时长780 s，最大车速为50 km/h，平均速度为19 km/h[2]。由于城市路况循环在NEDC测试中占比很高，所以可以认为低速复杂的城市路况是电动汽车主要的耗能场景。

电机驱动器作为电动汽车驱动系统的重要部件，是保障汽车性能和可靠性的核心。一般电动汽车电机驱动器的直流母线电压300～500 V不等，保时捷Taycan为了追求更高的最大输出功率其直流母线电压高达800 V。然而城市路况下电机输出功率较低，其输出电压与直流母线电压的比值较小，驱动器处于低调制比的工作状态。此时开关过程中死区效应等因素引起的电压损耗将无法忽略不计。文献[3]提出了5种影响输出电压的开关损耗模型以研究基于硅器件的驱动器与基于碳化硅器件的驱动器之间的不同，并指出其中死区效应对输出电压的影响为主要因素。因此可以在近似计算开关过程带来的谐波时，重点关注死区效应引起的谐波，且死区效应引起的电压畸变随开关频率的上升而上升。在试验中发现电机低速运行时，硅器件驱动器的效率远小于碳化硅驱动器。文献[4]中研究了使用脉宽调制(Pulse Width Modulation, PWM)的调制波的双重傅里叶分解表达式，PWM调制波电压表达式表明开关频率越低PWM调制波越接近矩形波，带来的电压畸变越大。基于上述两种关于开关频率的特性，针对不同的调制波频率需要采取不同的开关频率，因此需要一个调制策略来确定不同工况下的开关频率，这种策略叫做变频脉宽调制技术。

变频脉宽调制技术一般有异步调制和同步调制两种策略[5-7]，异步调制的开关频率不变而基波频率变化，同步调制则开关频率随着基波频率的变化而同步变化，相互之间频率的比值固定。一般在低频载比使用异步调制，高频载比使用同步调制。文献[8]通过对PWM调制波进行双重傅里叶分解，获得了各次谐波与开关角度之间的数学关系表达式，用改变开关角度的方法消除特定次数的谐波。再运用负载电感的低通特性在消除低次谐波后对剩余的高次谐波进行滤波达到总谐波畸变率(Total Harmonic Distortion, THD的下降，这种调制方法被称为特定谐波消除脉宽调制(Selective Harmonic Elimination Pulse width Modulation, SHEPWM)。传统的SHEPWM一般是以电压THD最小作为优化目标的[9-10]，但是由于电感的存在使得最小谐波电压并不能得到最小谐波电流，而电流又往往是在电机驱动中最主要的被控变量。因此文献[11]提出了以谐波电流最小为优化目标的SHEPWM控制策略，但是由于文章没有提供精确的三相电流模型。文献[12]则针对谐波电流最小这个优化目标给出了更加精确的约束条件，得到了比较满意的电流谐波抑制性能。

以上关于降低谐波畸变率的方法中，都把负载简化成电阻与电感串联的简单模型来分析驱动器输出电流的质量，而本文以低速运行状态的电动汽车为研究对象，由于大部分电动汽车为了增加力矩会采用凸极永磁同步电机，所以无法将负载简单的看成电阻与电感串联的模型，必须先将三相abc坐标系下的电压方程进行解耦，通过派克变换得到d-q坐标系下的电压模型，才能得到准确的电机电流THD模型。然后推导了一种综合考虑开关损耗与PWM调制波损耗后的电流THD模型，并以开关频率为变化量，“电流总谐波最小”为优化目标，求解低速状态下的最优驱动器开关频率。

1 电流谐波模型

1.1 死区效应引起的电流谐波

图1是一个电压源型三相逆变器驱动的永磁同步电机系统。通常来说，功率半导体器件因为有一定的开通关断时间，所以为了防止桥臂直通会引入死区时间来使一个开关管完全关断后再打开另一个开关管。以a相为例说，在死区时间Tdt期间，上下开关S1和S4都处于关断状态，当ia>0的时候，二极管D4导通，输出电压为-Vdc/2；当ia<0的时候，二极管D1导通，输出电压为Vdc/2。

图1 PMSM驱动系统

因此，在图2(a)中理想情况下S4关断的同时S1会导通，此时电压输出的理想电压如图2(c)所示。而如图2(b)所示在引入了死区时间Tdt后，其持续时间内当ia>0时，会在S4关断而S1未开启时引入如图2(d)所示的伏秒损失；当ia<0时，会在S1关断而S4未开启时引入如图2(e)所示的伏秒增加。

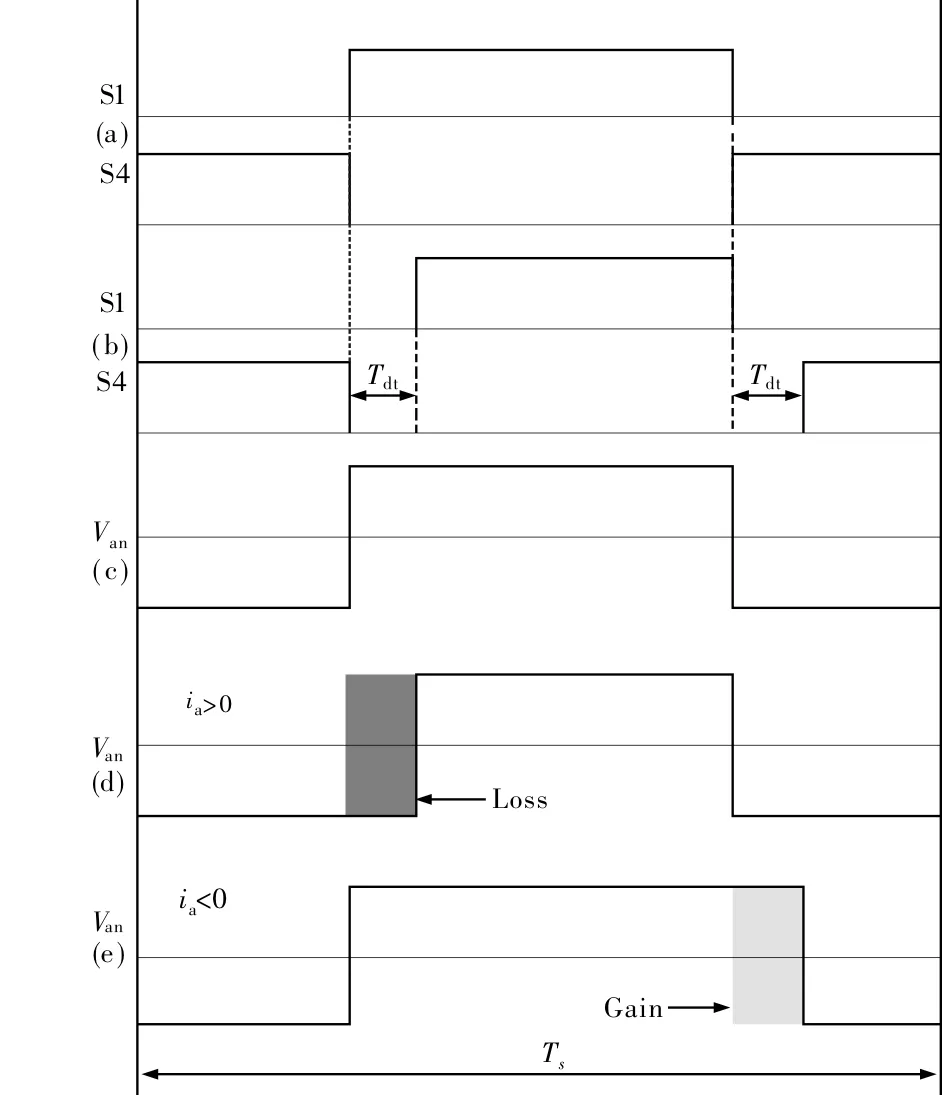
图2 开关状态与输出电压 (a)理想开关 (b)实际开关 (c)理想电压 (d)实际电压(ia>0) (e)实际电压(ia<0)

通过上述分析可以得到a相电压畸变在一个开关周期内的表达式：

(1)

通过式(1)可得到如图3所示的电压畸变波形图，可以得出死区时间带来的电压畸变是一个六阶梯波形，将这个波形进行傅里叶分解并派克变换后可以得到d轴和q轴上的电压畸变公式[13]：

图3 三相电流及其对应的a相电压畸变

(2)

(3)

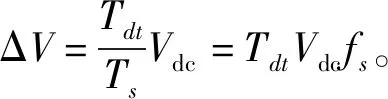
得到d、q轴上的畸变电压后就可以求得d、q轴上的畸变电流为

(4)

(5)

其中

式中，RS为定子电阻，Ld是d轴电感，Lq是q轴电感，ωm为电角频率。由此可得，死区时间引起的谐波电流有效值为

(6)

1.2 PWM调制引起的电流谐波

正弦波脉冲宽度调制是一种常见的调制手段，它通过一系列不同占空比的方波来模拟正弦波。因此PWM波形由载波频率(开关频率)与调制波频率(正弦波频率)共同决定。因此可以通过双重傅里叶分解得到a相电压公式[4]：

(7)

式中,x=ωmt，y=ωct，ωc为载波转速，M为调制比，Jl(x)为贝塞尔函数。

已知相电压表达式后，可以通过派克变换求得d、q轴电压表达式，这里先对余弦部分进行变换：

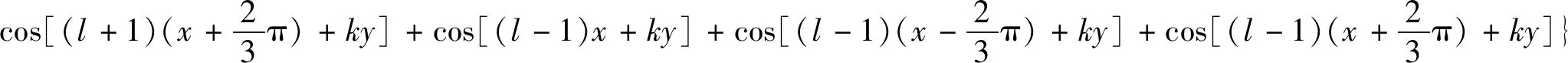
(8)

可以发现，只有当l+1=3n或者l-1=3n的时候这个公式才不为0。并且当l=2和l=4时，x前的谐波次数都为3。依次对整个公式进行派克变换都有类似结论，可以得到完整d、q轴电压表达式：

(9)

(10)

得到d-q坐标系下的PWM波形电压表达式后，根据电机模型可以求得d、q轴上的谐波电流有效值为

(11)

(12)

1.3 总电流谐波分析

通过式(6)、式(11)、式(12)可以得出一个综合考虑死区效应与PWM调制带来的谐波电流后的电流THD模型：

(13)

式中,I1为基波电流有效值。

从式(6)可以看出，死区效应带来的电流畸变有效值大小随平均畸变电压ΔV增大而增大，在死区时间与直流侧电压不变的情况下，则随开关频率的增大而增大；而从式(11)可以看出，PWM调制带来的电流畸变有效值在其余变量不变时随开关频率的增大而减小。显然，对于总谐波电流来说在确定的运行条件下存在一个开关频率使得其取值最小。

同时由于PWM调制波带来的电流畸变随着调制比M的减小而减小，因此只有在较低的调制比下，开关频率才能在一般IGBT的有效开关频率范围内(0～10 kHz)取得极值。

2 仿真参数选取和搭建

2.1 转速的选取

上文提到的NEDC是欧洲的一种电动汽车续航测试标准。我国在对纯电动汽车的综合里程续航测试的环节中，常常也采用NEDC的测试循环进行测试。

NEDC一般包含5个测试循环，其中有4个最高速度50 km、平均速度19 km/h的城市路况测试循环和一个最高速度120 km/h、平均速度62 km/h的高速路况测试循环。因此可以认为低速的城市路况是电动汽车最常见也是占比最多的运行工况。根据其城市循环的平均值，在计算仿真参数时取轮胎半径r=0.25 m则轮胎侧转速为ωT=20 rad/s，传动齿轮减速比为5。可以得到电机转速ωr=100 rad/s，采用4对极电机则可得到电磁角速度ωm=400 rad/s。

2.2 转矩的选取

一般家用轿车综合考虑车重和载人载货量可以选取2000 kg作为总重。而由于选取的转速较低，且视为匀速运动，所以在忽略空气阻力和没有加速度的情况下，简单的认为所需动力即为克服摩擦力即F=μmg=200 N，μ为滚动摩擦系数一般取0.01[14]。再根据轮胎半径和速比可以求得电机侧的最低转矩为8 Nm，考虑误差以及损耗，仿真中选取10 Nm作为电机负载转矩。

2.3 仿真模型搭建

仿真中永磁同步电机的模型参数如表1所示。

表1 凸极永磁同步电机仿真参数表

根据表1中的电机，采用了传统的矢量控制方法搭建了仿真模型。仿真采用id=0，电流内环、速度外环的基本控制结构。同时编写了一个根据式(13)的计算程序，通过仿真结果与计算结果的交叉对比验证计算结果的正确性和有效性。

3 仿真结果与分析

3.1 不同开关频率仿真分析

选取3 kHz、5 kHz、10 kHz的频率作为开关频率，分别运行仿真，得到相电流波形如图4、图5、图6所示。

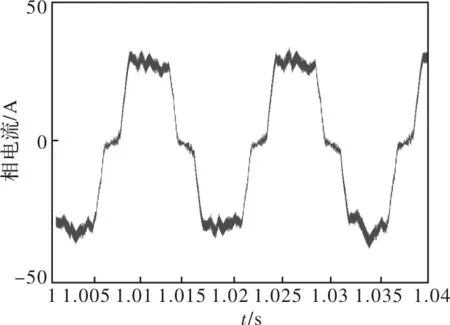
图6 10 kHz开关频率下的相电流波形

图5 5 kHz开关频率下的相电流波形

图4 3 kHz开关频率下的相电流波形

对比三幅图形可以明显的发现，3 kHz开关频率下相电流波形由于开关频率较低，带来的电流纹波较大，但是死区效应带来的电流波形畸变较小。10 kHz开关频率下相电流图形由于开关频率较低，带来的电流纹波较小，但是死区效应带来的电流波形畸变较大。5 kHz开关频率下相电流波形由于开关频率适中，电流纹波和电流波形畸变也适中。使用Matlab自带的FFT分析模块求解这三个电流波形的THD值，得到3 kHz、5 kHz、10 kHz开关频率下相电流的THD值分别是16.05%、13.80%、19.74%。可以发现5kHz开关频率下的电流THD最小。同时进一步仿真获得4700 Hz与4800 Hz开关频率下的相电流THD值分别为13.85%与13.67%。基本可以近似认为上述仿真条件下的最优开关频率在4800 Hz附近。

3.2 计算验证最优开关频率

通过使用Matlab自带的贝塞尔函数编写了一个根据式(13)的计算程序。程序以开关频率为变量，100 Hz为间隔单位，无穷项k、j分别取到10和100(更高次谐波忽略不计)，将仿真数据代入公式，计算每个开关频率下的电流THD值，一共得到四组不同死区时间下的“电流THD-开关频率”曲线如图7所示。

图7 不同死区时间下电流THD值的计算结果

当死区时间在4 μs的时候电流THD值在4800 Hz的时候取得最小值16.61%，和仿真结果基本一致。计算结果中电流THD值偏大主要是由于计算高频电流时忽略了电阻与集肤效应导致的。计算验证结果表明式(13)能够相对精确的计算不同频率下电流THD值，并求得一个最佳的开关频率供电机使用。而当死区时间的设定值改变时，最优开关频率也不断在改变，1 μs到4 μs的最优开关频率分别为9600 Hz、6800 Hz、5500 Hz、4800 Hz。可以得出当设定的死区时间变小的时候最优开关频率也会相应变大，当使用碳化硅等新功率器件材料时，可以将死区时间设定的更低以获得更高的最优开关频率。将死区时间设定至碳化硅器件才能达到的值时，其“电流THD-开关频率”曲线如图8所示，此时死区时间为0.4 μs。计算得出的最佳开关频率为15.1 kHz，此时的电流THD值为5.25%，而当开关频率取为20kHz时电流THD值也仅有5.65%。因此当采用宽禁带功率半导体器件时，在低速段则可以不需要降低开关频率来降低电流THD值，甚至可以在全速范围段都采用一个固定的开关频率(如20 kHz)使得控制算法能更加简洁，滤波电路的设计能更加的小巧。

图8 0.4 μs的死区时间下电流THD值的计算结果

4 结 论

本文针对电动汽车在城市路况下低速运行时的电动机相电流THD值进行优化。主要通过对死区效应产生的电压畸变和PWM调制算法产生的电压畸变进行畸变电压公式推导。将推导获得的畸变电压通过派克变换到d-q轴坐标系上代入电机电压方程求得d-q坐标系下的畸变电流。再将畸变电流求和得到了同时由死区效应和PWM调制算法影响的电流THD值表达式。以开关频率为变量，获得指定约束条件下的最小电流THD值。

仿真结果表明，电机输出电流波形和驱动器的开关频率密切相关，较低的开关频率会带来较大的电流纹波，而较高的开关频率会带来较大的电流波形畸变。通过不断改变驱动器开关频率，可以发现在仿真设定的条件下，死区时间为4 μs时，4800 Hz是一个较优的开关频率。将仿真中的数据模型代入式(13)计算得到死区时间为4 μs 时，4800 Hz为最优开关频率，说明计算结果与仿真结果基本一致，验证了公式的可靠性。

同时本文还指出具有更高开关速率的功率器件，如碳化硅功率器件，不仅在高速电机上有优势，对于城市路况下的电动汽车同样可以凭借其高速的开关速率以设置更低死区时间，从而使电机获得更好的低速性能外，还可以统一全速段开关频率以使控制算法更加的简洁，且外部的滤波电路能够设计的更加的小巧。