利用动力学去耦合脉冲增大和调节量子相干性和三体纠缠

贺启亮,丁 敏,宋晓书,肖勇军

(贵州师范大学物理与电子科学学院,贵阳 550001)

1 引 言

量子相干性(quantum coherence)起源于量子态叠加原理,被认为是一种重要的物理资源,在量子物理与量子信息过程中扮演着非常重要的角色[1-8]. 根据量子力学理论,量子相干性可以利用波函数的叠加或者密度矩阵的非对角元来进行描述. 由于各种各样的量子效应,比如量子干涉、量子霍尔效应等都与量子相干叠加有着非常密切的关系. 因此,量子态之间的相干叠加也被认为是非经典关联(例如量子纠缠(quantum entanglement),量子失谐(quantum discord)等)存在的必不可少的先决条件. 近年来,许多研究都指出量子相干性可能是一种更为普遍,更为基础的量子资源[9-15]. 特别在开放量子系统中,相较于其他非经典关联,量子相干性将更加强壮,而且在某些特定的情况下,其可以被冻结保持不变[16]. 尽管量子相干性如此重要,但是其研究却发展相对缓慢,直到最近Baumgratz等人才提出了一个严密的理论来系统地刻画量子相干性[17]. 基于这个理论,许多满足相干性度量约束条件的计算方法开始被提出,比如基于范数的相干性、基于相对熵的相干性[17]、基于skew信息的相干性等[18-19]. 另外,在生物物理中与量子相干性相关的实验证据也陆续被报道[20-21].

另一方面,伴随着量子诱捕技术[22]和高品质光学微波腔[23]的快速发展,使得量子电动力学系统成为执行量子信息任务和完成量子信息过程最理想、最有潜力的候选者之一[24-25]. 腔电动力学系统是将原子诱捕在光学微波腔中来实现的. 在系统中,原子的特征状态可以存在相对较长的时间,这一先天性质使得它非常适用于量子信息的存储. 同时在系统中,由于相对密闭的环境,光子也能更好地携带和传输量子信息. 此外,在量子物理的基础研究中,特别是在相干性、非定域性、测量等方面,腔量子电动力学系统都扮演着非常重要的角色[26]. 强耦合的腔电动力学系统实验为量子控制和量子信息科学本质特征的证明提供了有力的帮助,而且还为量子计算和量子通信技术的发展提供了非常重要的技术支持[27-29].

综上所述,国内外研究者在量子相干性特性研究[9-16]、量子相干性度量方法[17-19]、腔量子电动力学系统中量子关联研究[24-26]以及基于腔量子电动力学系统的量子信息任务执行[27-29]等方面都开展了许多的研究工作,但是对于利用去耦合脉冲在腔量子电动力学系统中增大量子相干性和调节三体纠缠的研究还未见相关报道. 鉴于此,本文基于腔量子电动力学系统,研究了利用动力学去耦合脉冲增大两目标原子之间的量子相干性和非经典关联. 计算表明,两个原子之间的量子相干性和非经典关联可以通过在系统中加入一连串的动力学去耦合脉冲来进行调节和增加. 此外,本文还利用迹距离的方法探讨了动力学去耦合脉冲增加两原子之间量子相干性和非经典关联的原因,发现动力学去耦合脉冲能够控制和加速量子信息从其他子系统回流到两个原子中去,并减少两原子子系统和其他子系统之间的量子信息流动,从而增加两个原子之间的量子相干性和非经典关联. 最后,借助态制备保真度的方法研究了系统中三体纠缠出现的情况. 结果显示,随着时间的演化,系统中会出现三体纠缠,三体纠缠出现的周期可以通过动力学去耦合脉冲来进行调节,并且系统出现三体纠缠的时间区域可以通过调节脉冲间隔时间来增加.

考虑一个由两个二能级原子A、B与光腔进行相互作用组成的系统(如图1所示).

图1 本文研究系统简要模型图

H=H0+Hint+Hp

(1)

此处,

(2)

(3)

Hp=V(t)a+a

(4)

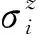
UpU0Up≅e-iπa+ae-i(H0+Hint)Te-iπa+a=

-e-i(H0-Hint)T

(5)

利用(4)式和(5)式,不难得到当加入动力学去耦合脉冲后,在时间t=2N(T+τ)+tx时系统随时间演化算符为:

(6)

Uc=Up(τ)U0(T)Up(τ)U0(T)

(7)

初始,假设两个原子制备于量子关联态,腔场制备于真空态,即:

|ψ(0)〉=(cosθ|gg〉+sinθ|ee〉)⊗|0〉

(8)

利用系统的时间演化算符U(t)并对腔场求迹,在标准正交基矢(|ee〉,|eg〉,|ge〉,|gg〉)下可以得到两个原子之间的约化密度矩阵为:

(9)

此处,

ρ11(t)=(cosθ)2|M1(t)|2

ρ33(t)=(cosθ)2|M3(t)|2

ρ44(t)=(cosθ)2|M4(t)|2+(sinθ)2

ρ22(t)=(cosθ)2|M2(t)|2

(10)

这里,

M1(t)=3(〈ee0|U(t)|gg2〉+〈gg2|U(t)|

|eg1〉+〈eg1|U(t)|ge1〉+〈ge1|U(t)|

eg1〉+〈ge1|U(t)|ge1〉)

M2(t)=〈eg1|U(t)|ge1〉-〈eg1|U(t)|eg1〉+

〈ee0|U(t)|eg1〉+〈ge1|U(t)|eg1〉-〈ge1|

U(t)|ge1〉+〈ge1|U(t)|ee0〉+〈gg2|U(t)

M3(t)=〈eg1|U(t)|eg1〉-〈eg1|U(t)|ge1〉-

〈ge1|U(t)|eg1〉+〈ge1|U(t)|ge1〉-

eg1〉+〈ge1|U(t)|ge1〉)+ 3(〈ee0|U(t)|ee0〉+

(11)

3 动力学去耦合脉冲对相对熵量子相干性的影响

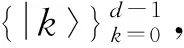
(12)

标记所有的非相干态为一组集合,记为IC. 而最大相干态在Baumgratz等人的文章中也已经给出,其形式为

(13)

任何一个有效计算量子相干性的度量方法都必须满足以下四个条件[15,17]: (1)C(ρ)≥0,当且仅当量子态δ是非相干态中的任意一个态时,C(δ)=0；(2)在非选择相干完全正定保迹(ICPTP)映射Λ作用下,其是单调的,即:C(ρ)≥C(Λρ)；(3)在选择映射ICPTP取平均情况下,其是单调的,即:C(ρ)≥∑nqnC(Λnρ)；(4)在量子态为混合态的情况下,其是非递增的,即:C|∑ipiρi|≤∑iC(ρi).

由于相对熵量子相干性测量方法满足上面列出的所有四个条件,所以是一个良好且有效的测量量子相干性的方法. 根据文献[17],相对熵量子相干性Cre可以被定义为:

Cre=S(ρdiag)-S(ρ)

(14)

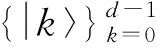
另一方面,除了量子相干性,本文还研究了动力学去耦合脉冲对两个原子之间的非经典关联(量子纠缠和量子失谐)的影响,并对比了它们与量子相干性动力学行为的异同点. 这里,为了度量量子纠缠,本文将采用Wootters的concurrence[32]. 对于一个双量子比特系统,concurrence可以被定义为:

(15)

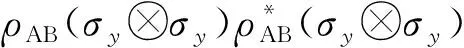
(16)

另外,对于量子失谐,本文采用Olliver和Zurek[33]引入的方法来进行计算. 他们将量子失谐定义为总关联和经典关联的差异,其能被表示为:

Q(ρAB)=I(ρAB)-CC(ρAB)

(17)

对于一个两体量子系统来说,总关联能够通过量子互信息来定义:

I(ρAB)=S(ρA)+S(ρB)-S(ρAB)

(18)

这里S(ρ)=-Tr(ρlogρ)为冯诺依曼熵,ρA=TrB(ρAB)和ρB=TrA(ρAB)分别是子系统A和B的约化密度矩阵. 对于式(9)这样的X结构密度矩阵来说,其冯诺依曼熵可以表示为

(19)

此处,

(20)

(21)

根据对其中一个子系统进行测量所得的最大信息量,经典关联能够被定义为

(22)

这里,{Bk}是在子系统B上的一组完备的投影,S(ρAB|{Bk})=∑kpkS(ρk)是基于测量的量子条件熵,ρk=1/pkTrB[(I⊗Bk)ρAB(I⊗Bk)]是条件密度算符,pk=Tr(AB)[(I⊗Bk)ρAB(I⊗Bk)]是得到相应条件密度算符的概率. 接下来,根据(9)式和参考文献[34]所介绍的方法,两个原子间量子失谐的解析表达式可以被计算并得到. 但是,因为这个表达式过于繁冗和复杂,所以在这里不列出它的具体形式.

下面,本文将就动力学去耦合脉冲对两个原子之间量子相干性(quantum coherence)与非经典关联(量子纠缠和量子失谐)的影响开展研究,并把它们的动力学性质进行对比. 图2、图3和图4描画了系统中两个原子之间量子coherence Coh(ρ)、量子concurrenceE(ρ)和量子discordQ(ρ)随时间t和脉冲间隔T变化的演化图像,其中参数θ=π/15,g=1以及τ=0.01.从图中可以发现,量子coherence和非经典关联都会出现周期性的振荡,也就是说随着时间的演化,它们都会先减小然后再增大. 通过对比可以看出,它们的动力学演化行为大致是类似的,但是其变化周期并不一致,即它们并不是同步变化的. 其次,从图中不难发现,当加入动力学去耦合脉冲之后,两原子之间的量子coherence和非经典关联都能够通过调节脉冲之间的时间间隔T来增大,这一情况意味着动力学脉冲可以增加量子coherence和非经典关联,并在时间的演化过程中加快其回复到初值. 这个现象的物理解释是动力学去耦合脉冲抑制了原子与腔场之间的相互作用,防止了两个原子之间量子coherence和非经典关联的消失. 这里,当选择不同的θ时,得出的结论与此处所得结论是一致的.

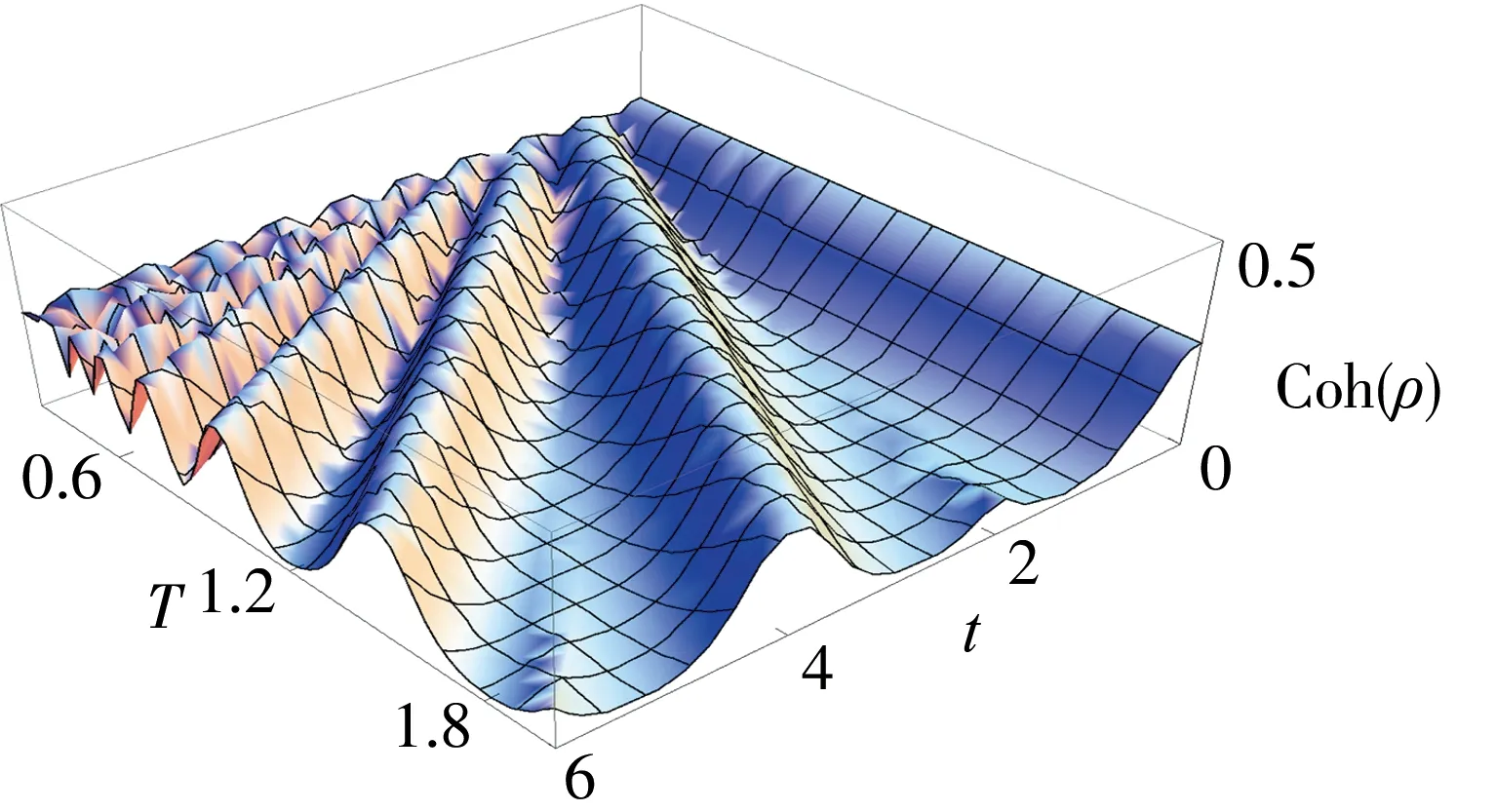
图2 两个原子之间的量子Coherence Coh(ρ)与时间t和脉冲时间间隔T的关系,其中

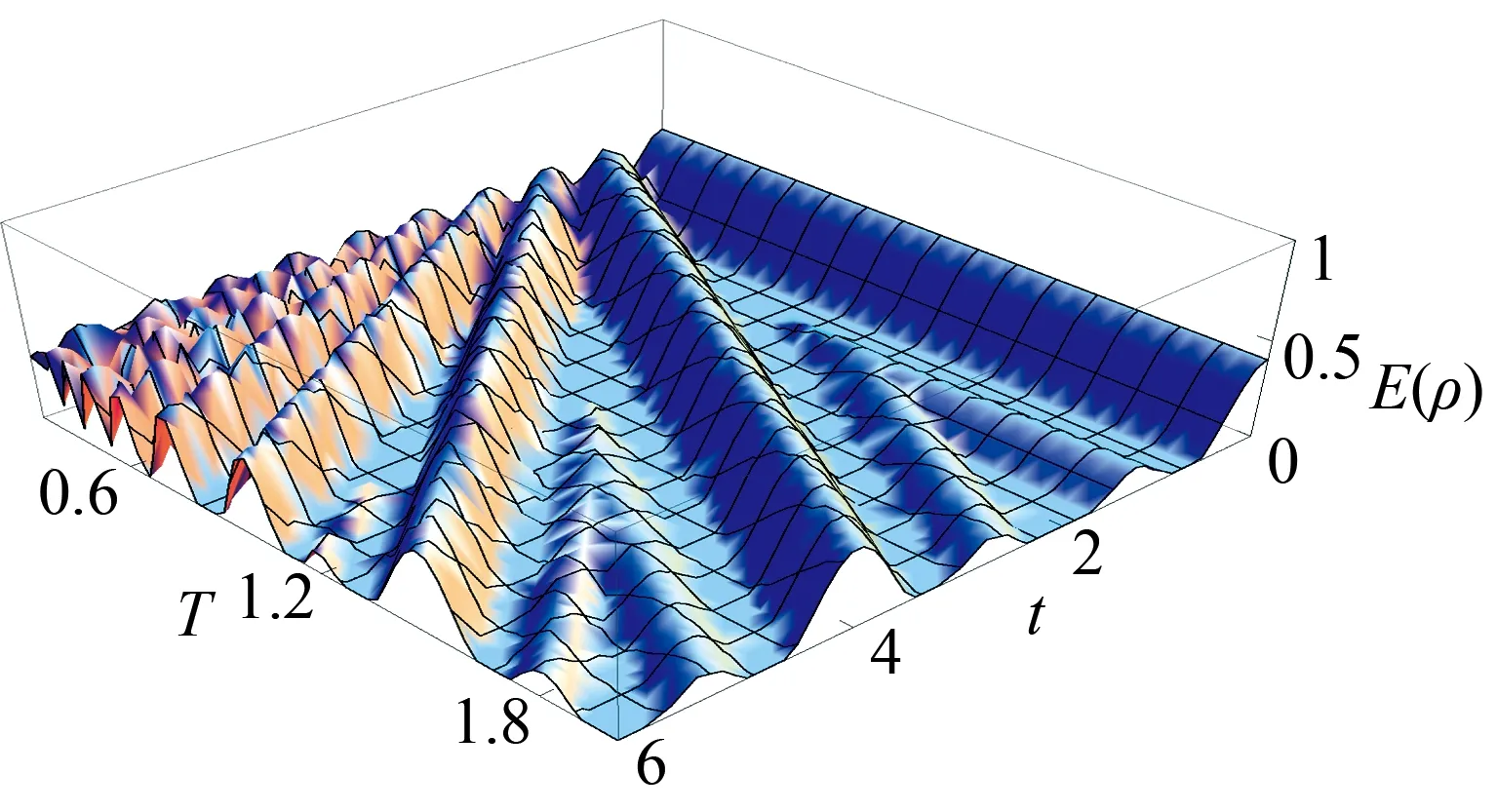
图3 两个原子之间的量子纠缠E(ρ)与时间t和脉冲时间间隔T的关系,其中

图4 两个原子之间的量子失谐Q(ρ)与时间t和脉冲时间间隔T的关系,其中

接下来,本文将展示不同时间间隔的脉冲对两原子间量子coherence和非经典关联的影响.图5、图6和图7针对脉冲不同的时间间隔T,把两原子间的量子coherence Coh(ρ),量子纠缠E(ρ)和量子discordQ(ρ)分别刻画为了随时间t变化的图像.从图中能够很清楚地看到两个原子之间的量子coherence Coh(ρ)、量子纠缠E(ρ)和量子discordQ(ρ)都能够通过加入脉冲来增加其数值,同时它们在时间点2N(T+)上能够恢复它的初始值. 另外,从图中也可以很明显地显示出量子coherence Coh(ρ),量子纠缠E(ρ)和量子discordQ(ρ)的变化周期都等于2T,并且当脉冲时间间隔

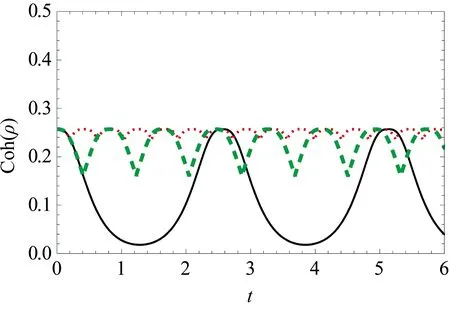
图5 两个原子之间的量子coherence Coh(ρ)随时间t演化的图像,其中

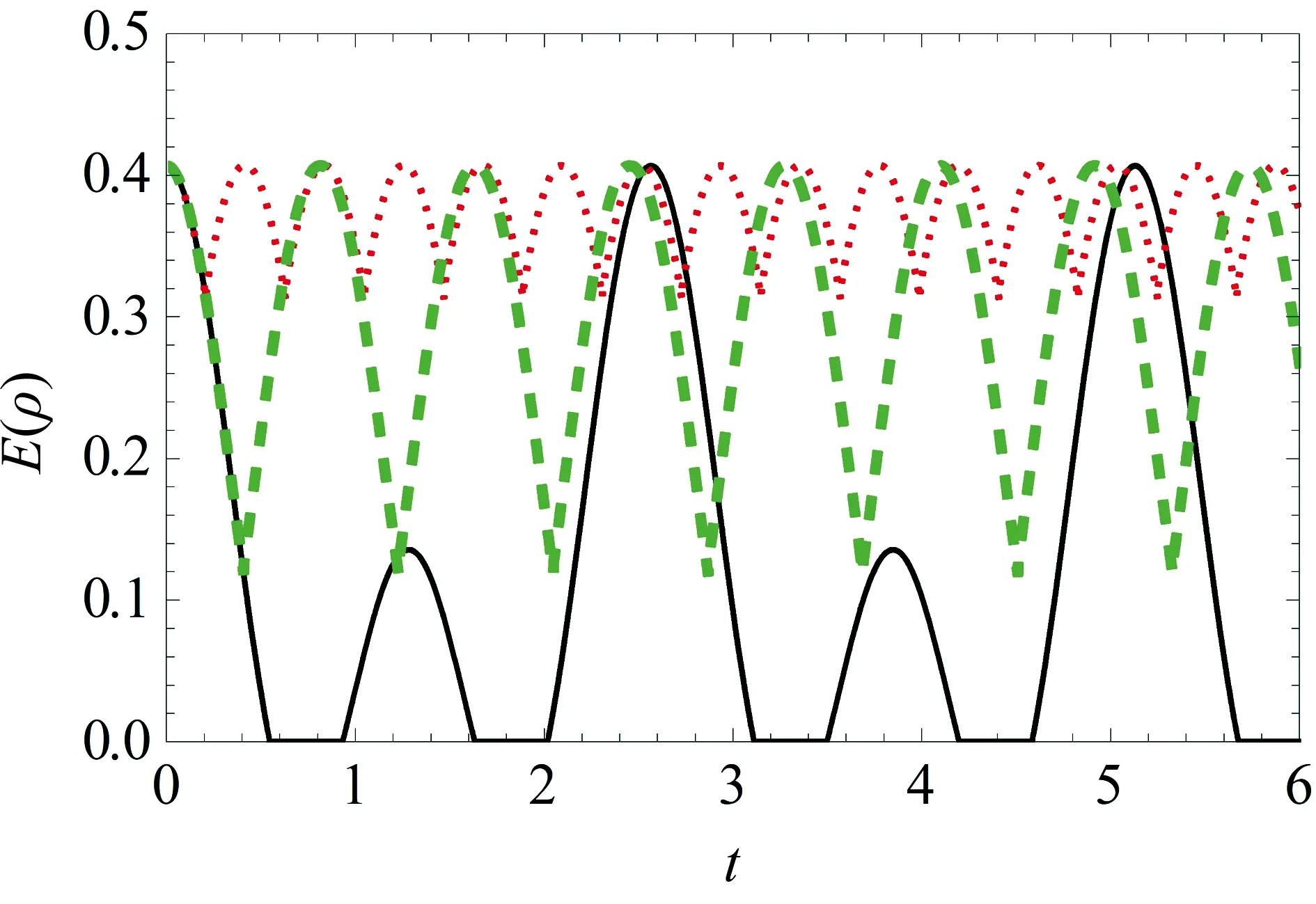
图6 两个原子之间的量子纠缠E(ρ)随时间t演化的图像,其中

图7 两个原子之间的量子失谐Q(ρ)随时间t演化的图像,其中

T越小时,量子coherence和非经典关联的振幅也会越小. 值得注意的是,在自由演化时,系统中将出现纠缠突然死亡的现象,但是这个时候的量子失谐和量子coherence并不为零,这证明了量子失谐和量子coherence或许是一种更为基本的非经典关联. 此外,还可以看出系统中出现的纠缠突然死亡现象会随着动力学去耦合脉冲的加入而消失. 综上所述,可以发现在系统中加入动力学去耦合脉冲能够增大两个原子间的量子coherence和非经典关联数值,控制它们变化的周期,保护它们初始存储的量子coherence和非经典关联. 这里,当选择不同的时,得出的结论与此处所得结论是一致的.

4 动力学脉冲对系统中量子信息转移的影响

为了能够进一步了解动力学脉冲增加两原子之间量子相干性和非经典关联的原因,本文将使用迹距离的方法研究动力学去耦合脉冲对原子与腔场之间信息流动的影响,从而找寻相关现象发生的可能因素. 这里首先简单回顾一下迹距离的定义及其相关性质. 迹距离由Breuer等人引入,用于探究系统与环境的初始关联对开放系统动力学演化的影响[35-36],同时,作为度量方法可以用来描述量子系统中信息的转移和测量开放系统非马尔科夫行为,一些相关的结果已被近来的实验所证实[37-38]. 迹距离作为两个量子态ρ1和ρ2之间差别程度的度量,其被定义为[35]:

(23)

D(Uρ1U†,Uρ2U†)=D(ρ1,ρ2)

(24)

特别,迹距离能够表达为对所有投影算符Π求迹的最大值,也就是:

(25)

这个式子表明对ρ1和ρ2进行测量时,所能得到区分程度的上限. 因此,迹距离D(ρ1,ρ2)可以解释为表征两个量子态ρ1和ρ2的差异程度的测量方法.

下面开始研究动力学去耦合脉冲对整个系统中信息流动的影响,并结合其对量子相干性的影响进行讨论. 根据方程(8)、(9)以及(23),在考虑系统加入动力学去耦合脉冲后,t时刻两个原子之间的迹距离能够被推导得出为:

|M2(t)2|+|M3(t)2|+|M4(t)2|-1)

(26)

这里的M1(t),M2(t),M3(t),M4(t)已在(11)式中给出.

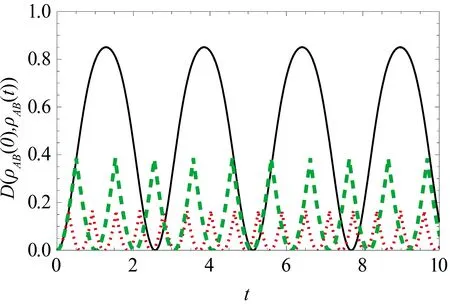
图8 迹距离D(ρAB(0),ρAB(t))随时间t演化的图像,其中

图8考虑未加入动力学去耦合脉冲和加入不同时间间隔动力学去耦合脉冲的情况,本文把两原子间的迹距离D(ρAB(0),ρAB(t))展示为随时间t变化的函数. 从图中的黑色实线(未加入脉冲)能够很清楚地看出,迹距离D可以超过它的初值,这个情况与初始两个原子间的量子信息流入到光腔相对应,也就是说初始两个原子所拥有的信息泄露到了光腔中. 由图中黑线的变化,还可以发现随着时间的变化迹距离D的数值会增加以及减少,这种变化分别与两个原子子系统中信息的增加和减少相联系. 其中,迹距离D增加的现象说明,两个原子系统中所拥有的量子信息将会减少,也就是说两个原子之间的量子相干性,非经典关联在随时间演化的过程中会被破坏,进而变成没有量子特性的状态. 这个现象暗含了两个原子之间的初始量子态将会改变,同时将会失去执行量子信息任务所需要的量子特性.

将图中黑色实线(未加入脉冲)与绿色虚线(脉冲时间间隔T=0.5),以及红色点线(脉冲时间间隔T=0.3)进行对比,不难发现两原子间迹距离D的值将会由于动力学去耦合脉冲的加入而减少. 而且当缩短所加入脉冲的间隔时间T时,两原子间的迹距离将会变得更小. 这些都意味着动力学去耦合脉冲能够抑制两个原子与腔场之间的相互作用,并且加快信息回流到两个二能级原子系统中去,从而保护两个原子之间的量子相干性和非经典关联. 这一现象的物理解释是动力学去耦合脉冲不仅可以防止两个原子之间的量子信息流入到其他不同的子系统中,而且可以减少其他子系统间信息回流进入两个原子系统中,从而保护两个原子子系统不受影响.这个结果表明,通过在系统中加入动力学去耦合脉冲,可以保护执行量子信息任务所需要的两个原子间初始存在的量子关联和量子特性.

对于如何从众多纠缠态或者可分离态中区分出真正的三体纠缠态存在着许多判定标准. 例如Mermin-Klyshko不等式[39-40]、态制备保真度[41-42]等. 这里,本文采用态制备保真度去研究系统中出现的三体纠缠.

初始,假设整体系统处于量子态:

|φ(0)〉=(cosθ|eg〉+sinθ|ge〉)⊗|0〉

(27)

将(6)式中系统随时间演化算符和(27)式相结合,不难得到整个系统随时间演化的密度矩阵为

(28)

其中,

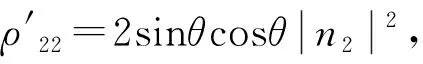
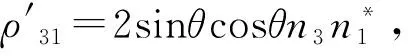
(29)

这里,

(30)

对于一个三体纠缠态ρx来说,态制备保真度F能够被定义为:

F(ρx)=〈GHZ|ρx|GHZ〉

(31)

此处,|GHZ〉是三体纠缠GHZ态,对于真正的三体纠缠成立的充分条件为:

(32)

根据三体纠缠GHZ态形式选择的要求[43],本文中选择三体纠缠GHZ态为[44]:

i|gg1〉]

(33)

(34)

另外,对比图中红色点线和黑色实线,不难发现当加入动力学去耦合脉冲后,态制备保真度F(ρ)超过1/2的区域将会增多. 这表明随着时间的演化,系统出现三体纠缠的频率将会增多,周期性变化的时间将会减少. 其变化周期与脉冲时间间隔T之间存在着密切的联系,并且近似的等于脉冲时间间隔2T. 这一现象意味着,系统中出现三体纠缠的时间可以通过动力学去耦合脉冲来进行调节,且可以通过改变加入脉冲的时间间隔来控制系统中三体纠缠的变化周期,从而增加系统中出现三体纠缠的时间区域.

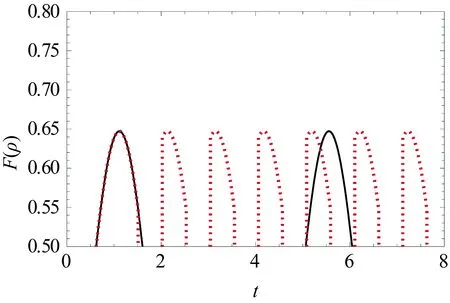
图9 系统的态制备保真度F(ρ)随时间t演化的图像,其中

未加入脉冲F(ρ)(黑色实线),加入时间间隔T=0.5脉冲的F(ρ)(红色点线).

T=0.5(red dotted line) and without dynamical decoupling pulses (black solid line).

6 结 论

本文研究了动力学去耦合脉冲对腔量子电动力学系统中目标原子间量子coherence以及非经典关联(量子纠缠和量子失谐)的影响. 结果显示,两个原子之间的量子coherence、量子纠缠和量子失谐的数值能够通过应用动力学去耦合脉冲来增大,而且其数值增加的幅度会随着控制脉冲时间间隔T的缩小而变大. 两原子之间的量子coherence、量子纠缠和量子失谐在时间点2N(T+τ)能够恢复它的初始值,也就是说,量子coherence与非经典关联的变化周期等于2N(T+τ),而且其振荡的振幅会随着脉冲时间间隔T的变短而减小. 这意味着,如果动力学去耦合脉冲的时间间隔无限接近于无穷小(即:T→0),那么两原子之间的量子coherence和非经典关联将一直在初始值上保持不变.

此外,本文还利用迹距离的方法研究了动力学去耦合脉冲增加量子coherence和非经典关联的原因. 当应用动力学去耦合脉冲之后,两原子之间的迹距离将会减小,这说明动力学去耦合脉冲能够控制和加速量子信息从其他子系统回流到两个原子中去,并减少两原子子系统和其他子系统之间的量子信息流动,从而增加两个原子之间的量子信息,提高两原子间的量子coherence和非经典关联.

最后,本文研究了动力学去耦合脉冲对系统三体纠缠出现时间区域的影响. 通过结果可以发现随着时间的演化,系统中会出现三体纠缠现象. 但是,系统三体纠缠出现的时间区域是有限的,并存在较长的周期时间间隔. 这一结果说明,随着时间的演化系统中三体纠缠将会消失,并在经过较长时间间隔之后才能重新出现. 然而,值得注意的是,当加入动力学去耦合脉冲后,系统中出现三体纠缠的时间区域将会增多,同时三体纠缠出现的时间周期也可以被缩短. 这意味着可以通过动力学去耦合脉冲来调节和控制系统三体纠缠出现的区域,减少三体纠缠出现的周期时间间隔,增加三体纠缠出现的时间.