网络性能数据恢复算法

欧阳与点，谢鲲

湖南大学信息科学与工程学院，湖南 长沙 410006

引 言

网络性能数据的监测是网络设计、运维和管理的核心问题[1-2]。获取全网端到端的性能数据对于有效地进行异常检测、排除网络故障、确定故障位置至关重要。但是，由于以下两种原因，当前的网络监测系统存在数据不完整的问题：

节约测量成本。在实际的网络监测系统中，全网的监测会带来较高的测量成本。对于规模为的网络，如果要测量全网端到端路径的性能，需在每对网络节点之间发送探测数据包，测量代价为O(n2)[3-5]。为了降低成本，稀疏网络测量技术[6]利用网络性能数据之间的时空相关性来实现基于样本的测量，仅在一定的时间间隙内随机测量部分节点对之间的数据，其他路径的数据则通过稀疏数据重构来推测。

不可避免的传输丢失。在恶劣的通信和系统条件下，如网络拥塞、节点的恶意行为、监测设备故障，使用不可靠的传输协议传输性能信息会导致测量样本数据进一步丢失。

异常检测[7]和故障恢复作为网络状态跟踪和预测[8]的应用，对数据缺失非常敏感。无论是由于未测量还是传输丢失导致的性能数据缺失，从部分性能数据精确恢复缺失数据非常重要且具有挑战性。

从部分性能数据恢复完整数据的质量，高度依赖于推测技术，现已存在大量研究。传统的推测技术仅基于单空间信息[9-10]或单时间信息[11]设计，数据的恢复精度都很低。为了同时利用空间和时间信息，不少研究使用矩阵填充技术从低秩矩阵中恢复缺失的数据[6,12-16]。尽管这些方法在低数据缺失率下表现出了良好的效果，但是当缺失率较大时，由于基于二维矩阵的数据分析在提取信息方面存在局限性，恢复精度会受到影响。

为了更好地恢复数据，最近有一小部分研究开始将网络性能数据建模为更高维的数组——张量，并提出基于张量填充的算法以更精确地恢复缺失数据。张量是向量和矩阵的高阶泛化。基于张量的多线性数据分析[17-18]表明，张量模型可以充分利用数据中的多线性结构，提供更好的数据解读和信息精度。

为了利用张量强大的数据表达和信息提取能力，本文将网络性能数据建模为3 维张量，其表示K个时间间隙内I个源节点到J个目的节点之间的性能数据，由于性能数据是部分观测的，因此是存在缺失元素的稀疏张量。本文的目的是通过张量填充恢复缺失的性能数据。

为了建模网络性能数据的交互，现有的张量填充算法通常将源节点、目的节点和时间间隙的特征域投影到一个共享的子空间中，然后使用子空间的潜在因子向量的内积表示源节点和目的节点在特定时间间隙的关系。因此，它假设源节点、目的节点和时间间隙之间的关系是线性的。然而，实际的性能数据之间的关系更复杂[19]，不能被简单的线性模型精确表达，导致数据恢复的精度不高。

深度学习作为捕获复杂关系的有力工具，已经在计算机视觉[20-21]、自然语言处理[22-23]和语音识别[24-25]领域取得了巨大的成就。自编码器[25-26]利用神经网络去学习输入数据的潜在表达（压缩编码），然后从压缩的编码重构原始输入。本文基于自编码器设计了一个缺失数据恢复算法，将部分观测到的性能数据输入到自编码器中，通过重构输出恢复的数据作为缺失元素的估计值。

为了克服现有张量填充算法的缺陷，我们通过充分利用自动编码器的数据重构能力来研究和设计高精度张量填充的潜力和算法。尽管深度神经网络（Deep Neural Network, DNN）在图像领域上取得了良好的成绩，但基于深度神经网络设计张量填充算法恢复缺失数据仍面临一些挑战：

由于网络性能数据的低秩性，每个时间间隙的网络测量矩阵存在复杂的非线性局部相关性和全局关联。如何在保证恢复精度的同时，准确地学习内部关联，且最小化模型的参数规模成为挑战。

网络性能数据存在缺失，只有部分观测到的样本元素，这给使用深度神经网络带来了挑战。由于DNN 中没有标准的方法来处理稀疏的输入数据，因此应缓和缺失值对神经网络的影响。

鉴于上述挑战，我们提出一个深度卷积自编码器（Deep Convolution AutoEncoder, DCAE）的张量填充模型，它包含如下几种技术：

用少量共享的参数，学习非线性局部和全局特征。与传统的全连接网络相比，DCAE 基于卷积以局部连接和参数共享的方式使用更少的参数。随着网络层次的加深，DCAE 可以利用CNN 以分层的方式学习从局部范围到全局范围的复杂关系。

设计良好的技术，减轻神经网络训练中缺失值的影响。我们使用经验损失函数，阻止缺失值为反向传播过程提供错误信息。

我们在三个公开的真实网络性能数据集上的实验结果，证明了DCAE 的有效性。除了DCAE，我们还实现了其他4 种张量填充算法作为性能评估的基准，并讨论了DCAE 的收敛行为。

本文的其余部分组织如下：第1 节和第2 节分别介绍了相关工作和系统模型；第3 节介绍了DCAE 的详细设计；第4 节中通过实验评估了算法性能；第5节总结了本文的工作。

1 相关工作

稀疏网络测量技术采用基于样本的网络测量，只随机在一定时间间隙的部分节点对之间进行测量，再利用网络性能数据中的时空相关性，推断其他路径的数据。近期一些研究基于时间信息[9-10,27]或空间信息[11,28]恢复网络性能数据，然而这类算法仅利用空间信息或时间信息，恢复精度较低。

为了能够充分捕获网络性能数据中的时间与空间特征，SRMF[16]针对网络流量矩阵提出了一种时空模型，利用流量矩阵的稀疏表征，结合流量矩阵进行时间与空间约束（即相同时刻或相邻地理位置之间的网络测量数据相似）进行数据推测。随后，一些其他矩阵恢复算法被提出来进行数据推测[6,12-15,29-30]。相较于基于向量的恢复方法，基于矩阵的算法通常能够从性能数据中获取更多的信息从而达到更好的恢复精度。然而，二维的矩阵模型仍然无法充分获取网络性能数据中高阶结构化信息，例如，SRMF[16]中定义的流量矩阵尽管能够捕获网络数据在不同时刻的时间相关性以及源-目的对之间的空间相关性，却无法捕获网络中各节点之间的空间相关性。因此，基于矩阵模型的数据恢复算法精度依然较低。

近期的研究表明，相比于矩阵填充，更高维度的张量填充算法可以捕捉更多维度的特征。基于张量的数据恢复算法通常可以充分捕获数据内部的高阶结构化信息，并用更少的采样数目获得更高的数据推测精度。目前，张量填充已经应用于很多领域中，如信号处理[31]、多分类学习[32]、图像压缩、数据挖掘与计算机视觉[18,33]等。

近年来，一些张量恢复算法[17-18,34-35]被提出用于数据恢复。文献[36]提出将测量数据建模成三维张量，并设计了恢复算法。由于张量分解需要大量的计算，采用现有的张量分解算法进行性能数据恢复非常困难。文献[36]提出了一个连续的张量填充算法来快速解决这一问题。实际应用中网络数据的采样速率会随着网络中的数据流量的变化而变化，当采样速率变化时，每一天的采样数据矩阵大小都不一样，无法形成规则的张量，因此，文献[37]提出了一种面向动态网络的张量填充方案以解决由于不同采样速率形成的不规则的网络数据张量模型。另外，实际的网络流量数据中，局部数据间存在较强的相关性，利用这一性质可以提高数据恢复的精度。文献[38]提出局部子张量填充算法，利用子张量的低秩性来实现更加精确的数据恢复。

然而，上述算法都基于源节点、目的节点和时间间隙线性关系的假设，用潜在因子的内积表示张量的元素值，无法表示具有复杂内部结构的实际网络性能数据。

2 缺失数据恢复的张量填充模型

本节首先介绍缺失数据恢复的张量填充模型，然后介绍其局限性。如图1所示，我们使用张量来表示由个网络性能矩阵构成的三维数组，其中表示第个时间间隙的性能矩阵。矩阵的大小是和分别对应源节点和目的节点的数量。元素表示第个时隙内从源节点到目的节点的网络性能数据。

图1 3 维网络测量张量Fig.1 3-way network monitoring tensor

如图2所示，通过张量分解进行张量填充恢复缺失数据通常包含两步：（1）使用观测到的部分样本基于CP 分解[39-40]训练潜在因子向量；（2）使用训练好的因子向量推测张量的缺失元素。

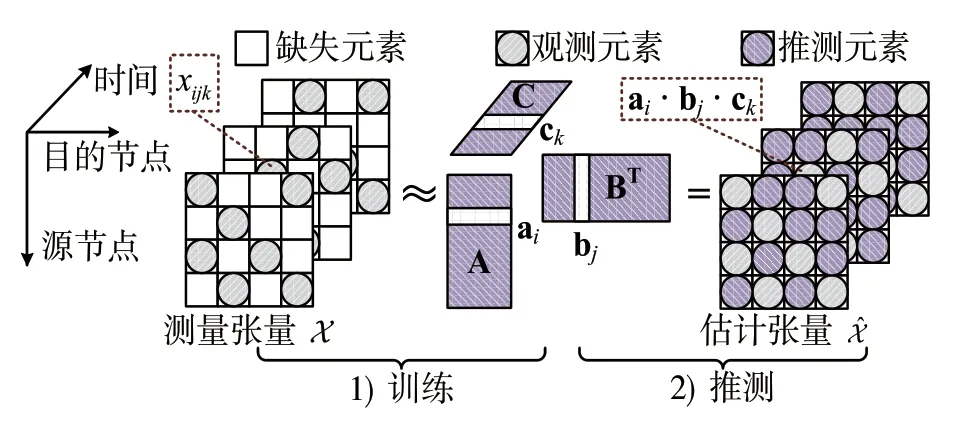
图2 通过张量填充恢复缺失元素的两个步骤Fig.2 Two steps to recover the missing data through tensor completion

3 DCAE 的详细设计

为了解决现有算法恢复网络性能数据的缺陷，本文提出一个深度卷积自编码器（DCAE）的张量填充模型。自编码器是由Kramer[26]提出的一种前馈神经网络，其以无监督的方式重构输入数据并输出。DCAE 的主要任务是给定部分观测数据，学习其内部的非线性复杂特征，估计缺失数据。

3.1 基于自编码器估计缺失数据

图3展示了基于自编码器估计缺失数据的基本思路。为了恢复不完整的性能张量，我们将每个时间间隙内部分观测的数据矩阵输入自编码器，然后输出已估计出缺失元素的矩阵。该框架包括两个部分，编码器和解码器。编码器将部分观测的性能矩阵作为输入，并通过一系列隐藏的神经网络层将其转换为潜在表达。在解码器端，通过另一组隐藏层，从中生成的密集重构，来预测缺失的数据元素。

图3 基于自编码器估计缺失数据Fig.3 Estimating the missing data based on autoencoder

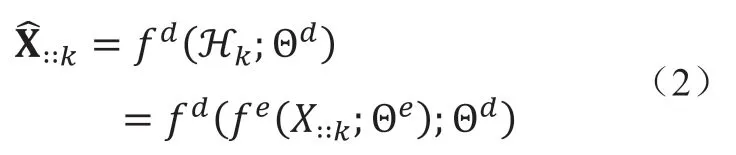
我们使用观测样本的均方误差(Mean Squared Error, MSE)表示填充问题的误差函数：

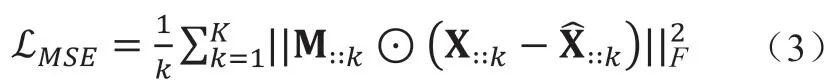
3.2 神经网络结构

卷积自编码器将自编码器中的全连接层更改为卷积层，扩展了传统简单自编码器的基本结构。由于以下两个目的，本文设计基于卷积自编码器的数据缺失恢复算法：

为了更好地利用网络性能矩阵中隐藏的相关性，更准确地恢复缺失数据。卷积神经网络使用过滤器，因此，卷积操作可以处理多维数据且保留数据的局部特征。如果我们使用传统全连接网络，则应首先将性能矩阵向量化，这会损失矩阵中的隐藏相关性。

为了构建更深的卷积自动编码器。卷积自编码器以局部连接和参数共享的方式、多层神经网络堆叠的形式组成，与传统的自动编码器相比，它使用的参数要少得多。传统的全连接自编码器需要较大的存储空间和更多的训练数据。因此，我们可以使用卷积自编码器构建更深的神经网络模型。

图4 网络结构Fig.4 Network architecture

为更好地利用性能数据中的非线性复杂特征以更准确地恢复缺失数据，我们使用卷积和反卷积过滤器设计了对称的卷积自编码器，即编码过程与解码过程对称，如图4所示。编码器端对输入矩阵进行下采样（即减小输入的大小），而解码器端对矩阵进行上采样（即增大矩阵的大小）。为了实现编码器的下采样，DCAE 采用了带步长的卷积。对于解码器，采用带步长的反卷积，这是卷积运算的逆过程。卷积过滤器和反卷积过滤器通过特征映射进行2D 卷积运算逐层提取特征。由于一个卷积过滤器只能从输入矩阵中提取一种类型的特征，因此，DCAE 中采用了多个卷积过滤器来提取更多类型的特征。连续的下采样/上采样操作会降低重构矩阵的质量。因此，我们提出了由一对步长分别为1 和2 的卷积/反卷积过滤器组成的下采样/上采样单元。我们使用ReLU[41]和Sigmoid 作为非线性激活函数。另外，为了构建更深的神经网络，除了输出层以外，每一层都使用层归一化（Layer normalization[42]）帮助模型收敛。

4 实验评估

本节评估所提模型DCAE 的性能，并对其收敛性进行了描述。

4.1 实验环境设置

数据描述。评估使用三个真实的网络性能数据集Abilene[43]、GÈANT[44]和WS-DREAM[45]。Abilene由12 个网络节点组成，记录了168 天内每5 分钟测量一次的流量，原始数据的观测率为100%。GÈANT 由23 个网络节点组成，记录了112 天内每15 分钟测量一次的流量，原始数据的观测率为88%。WS-DREAM 记录142 个用户和4500 个网络服务之间15 分钟一次共64 个时间间隙的流量，原始数据的观测率为63%。

性能指标。如表1所示，3 种评价指标误差率(Error Ratio, ER)、平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error,RMSE)用于评估DCAE。和分别表示性能数据张量的第个元素的原始值和恢复值，其中1 ≤i≤I，1 ≤j≤J，1 ≤k≤K。表示缺失元素的索引集合，所有算法都在缺失值上评估效果。

表1 性能指标Table 1 Performance metric

比较基准。除了DCAE，我们还实现了其他4种张量填充算法CPals[46]，CPnmu[47]，CPopt[35]和TKals[46]用于比较，其中前三个算法基于CP 分解模型，最后一个算法基于Tucker 分解模型。

参数配置。DCAE 由5 个卷积层和5 个反卷积层组成，卷积核大小为5×5，每层的卷积核数目分别 为[32,64,128,256,512,256,128,64,32,1]。DCAE 使用TensorFlow 的优化器Adam 进行小批量梯度下降更新，三个数据集Abilene、GÈANT 和WS-DREAM的学习率分别是10-3，10-2和10-3。

所有的张量填充算法都是迭代执行的，以训练所需的参数。为了公平比较，我们采用两个相同的迭代停止条件：(1)连续两次迭代之间的损失函数差值小于给定的阈值10-6；(2)达到最大迭代次数500。实验表明该设置可以保证各算法收敛到预期状态，见4.3，对于比较的传统算法这里不再赘述。为了获得更可靠的评估结果，我们重复每组实验20 次，并展示平均结果。

4.2 恢复性能比较

图5 DCAE 与线性张量填充算法比较Fig.5 Compare our DCAE with linear tensor completion algorithms

图5显示了5 种张量填充算法的对比实验结果。实验过程中，我们对每个数据集的现有数据进行10%-50%的随机采样，模拟数据缺失。意料之中，所有算法都随着采样率的增大达到更好的恢复效果。DCAE 的ER，MAE 和RMSE 明显更小，胜过所有其他传统的张量填充算法。即使当采样率非常低（10%）时，DCAE 的ER 约为0.3(Abilene)，而其他传统的张量填充算法的ER 为0.99(Abilene)，是DCAE 误差的3 倍。这些结果表明，DCAE 在提取测量数据中隐藏的复杂关系方面非常有效，可以显着提高恢复性能。

4.3 DCAE 的收敛性说明

本文使用损失函数的值评估所提算法的收敛行为，图6显示了DCAE 的收敛曲线。为了更清楚地观察DCAE 的收敛行为，因此该实验中将采样率固定为30%，且不设置迭代停止条件。显然，对于3 个不同的数据集，DCAE 的损失值都随着迭代轮数的增加而逐渐趋近于0 且稳定。注意到损失函数在收敛过程中有小幅抖动，这是小批梯度下降训练神经网络特性所致，最终网络的权值会收敛到局部最优，且在附近震荡。另外，三个数据集Abilene、GÈANT 和WS-DREAM 分别在第491 轮、第478 轮和第382 轮达到迭代停止条件，充分说明了迭代停止条件的合理性。

图6 DCAE 的收敛曲线Fig.6 Convergence curve of DCAE

5 总结与展望

本文提出了一种新的张量填充算法DCAE，可以为高层网络应用恢复缺失的测量数据。它可以捕获测量数据之间的非线性关系，具有高数据恢复精度，优于当前数据恢复算法。据我们所知，这是利用卷积自编码器解决张量形式的测量数据恢复问题的第一项工作。我们期望DCAE 强大的学习能力和张量表示高维数据隐藏结构的能力为高性能数据恢复和分析开辟新的途径。

利益冲突声明

所有作者声明不存在利益冲突关系。