信息中心网络中的内容命名粒度研究

张康宁，张珊，罗洪斌

北京航空航天大学，北京 100191

引 言

信息中心网络（Information-Centric Networking，ICN）[1-2]采用以信息为中心的通信方式替代现有的以端为中心的通信方式，能较好地满足人们对以信息为中心的通讯方式的需求，具有高效性、高安全性并支持客户端移动等特点。ICN 摒弃了传统的以IP 为细腰的协议栈结构，改为采用以信息名称为核心的网络协议栈，把信息名称作为网络传输的标识。

ICN 的内容名字通告策略主要是由其路由系统类型决定的，对于如CCN（Content-Centric Networking）[3]、NDN（Named Data Networking）[4]、TRIAD（Translating Relaying Internet Architecture integrating active Directories）[5]等采用无层次路由结构的ICN 架构，其名字通告通常采用基于洪范的方式，如下图1（a）所示，其中名字通告从A 节点不断向其他节点泛洪传播；而对于DONA（Data-Oriented Network Architecture）[6]等采用树形层次路由结构的ICN 架构，其名字通告通常是沿其树形结构逐级传播，如图1（b）所示，其中底层RH 节点的名字通告是沿树形结构向上级传递的。

ICN 的数据转发策略和传统TCP/IP 网络有所不同，ICN 的每个路由器都需要维护三个数据结构：待定请求表（Pending Interest Table，PIT）、前向转发表（Forwarding Information Base，FIB）和内容存储器（Content Store，CS）。其中PIT 负责对每个通过本路由器的请求包进行记录，并在内容包传回时找到对应请求包来时的端口进行转发；FIB 负责将请求包转发到目的端所在的端口；CS 则负责ICN 中路由器的数据缓存。

基于上述3 种数据结构，ICN 中的请求数据包转发主要分为两个步骤：（1）如果接收到请求包，则先在CS 中匹配内容缓存，如果有则直接返回相关内容，没有则进一步查询PIT；（2）如果PIT 中能找到相应的记录，则将请求包来时端口添加到该记录中，如果PIT 中没有相应记录，则查询FIB 并将该请求包转发至目标端口，同时将其记录在PIT 中。而ICN 中的内容数据包转发则是查询路由器的PIT，如果没有匹配记录则丢弃该包，如果有则根据匹配记录将其转发到一个或多个请求端口处，同时根据策略进行数据缓存并删除该PIT 记录。

这里以CCN[3]为例说明ICN 的数据转发流程，如图2所示，其中A、B、C、D、E 均为路由节点，C1、C2 为请求内容端，S 为服务提供端。在刚开始的时候S 通过基于洪泛的通告方式向网络所有节点通过其提供的服务，路由节点A-E 收到泛洪信息后计算并建立到S 的FIB 路由表。当C1、C2 先后向S 请求同一个服务时：（1）C1 向S 发出一个请求包，该请求包通过C 节点时首先查询CS 和PIT 无果，然后查询FIB 表决定下一跳为D 节点，同时在PIT 表中插入该请求及其源端口记录，其他路由节点执行相同动作直到请求包成功到达S；（2）S 收到请求包1 后向C1 发送一个内容包，当该内容包经过C节点时在节点的PIT 表匹配到对应的请求记录，在CS 中存储该内容包作为缓存后向对应请求记录的源端口转发，转发后删除该PIT 记录，其他路由节点执行相同动作直到内容包成功返回C1；（3）C2 向S发出一个请求包，当请求包经过C 节点时首先查询CS 并发现成功匹配，然后C 节点直接从CS 中取出并发送之前缓存的内容包给C2。

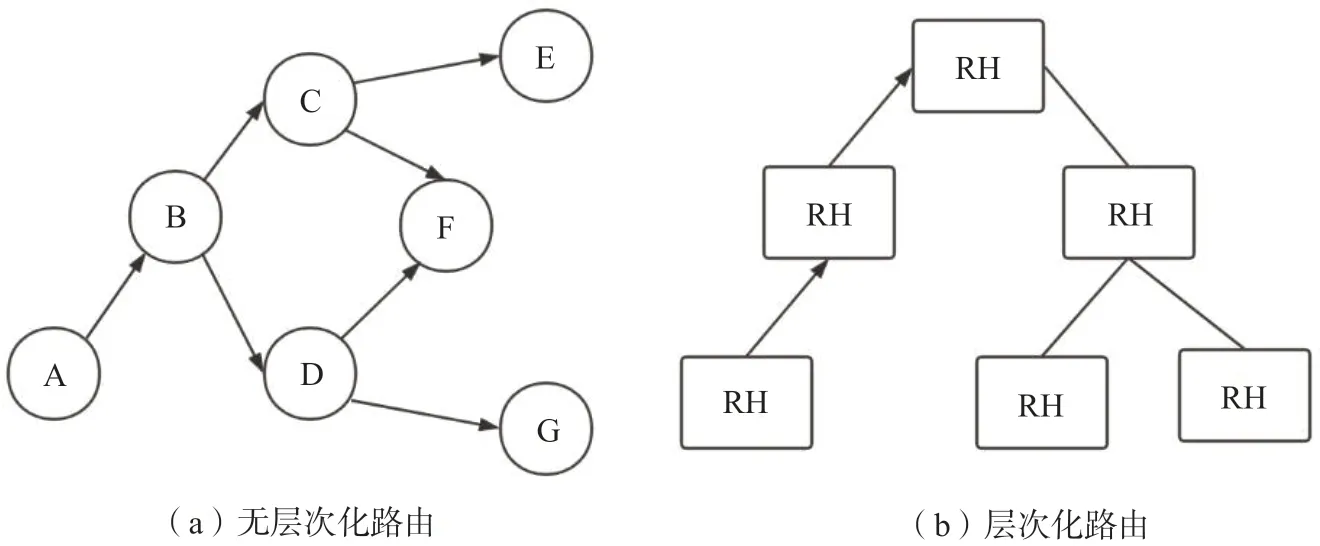
图1 ICN 中不同路由结构下的名字通告策略示意图Fig.1 Schematic diagram of name advertisement strategy under different routing structures in ICN

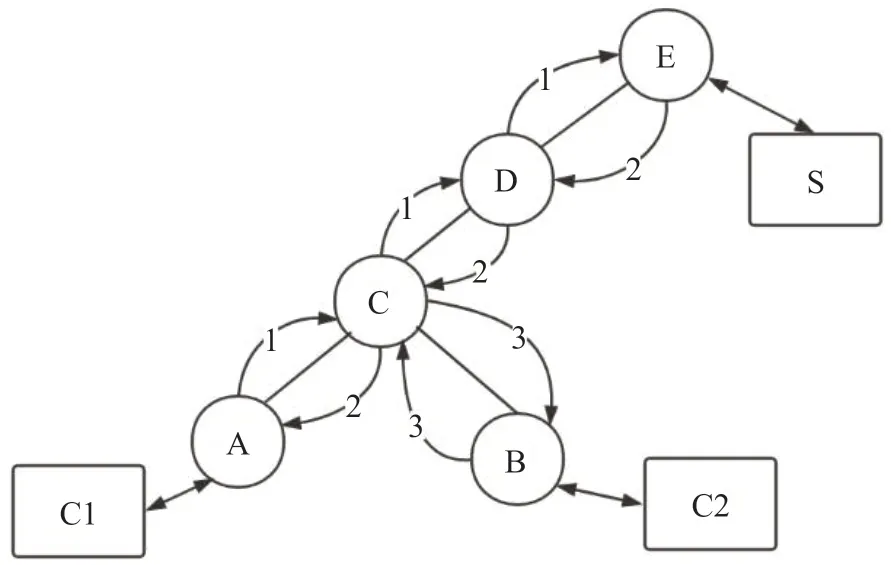
图2 ICN 中数据转发示意图Fig.2 Data forwarding diagram in ICN

从上面描述可以看出：在信息中心网络中，用户每次发送一个请求，只能返回该请求对应的内容（块），而不一定是一个完整的文件。对一个较大的文件而言，需要分成多个内容块，每个内容块都有一个独立的名字和相应的大小。我们定义命名粒度即对网络中发布内容进行命名的单个块的大小上限，即如果一个发布内容大于这个值则会据此先对其进行切分再命名。显然，命名粒度越小，一个大文件就可能被分成更多的内容块，也就会产生更多的内容名字。例如，一个80KB 的文件，当内容命名粒度为4KB 时，被分成20 个内容块，对应20 个内容名字；而当命名粒度为32KB 时，则被分成3 个内容块（如大小分别为：32 KB、32KB、16KB），只需3 个内容名字；若命名粒度为100KB，则该文件不用分块，只用一个名字即可。因此，内容命名粒度对内容名字的数量有重要影响，这个影响在ICN 的总体转发效率中占据了非常重要的地位。因为ICN 是以名字来作为转发标识的，相应的网络中名字的数量规模很大程度上决定了网络中路由器的条目规模，以及路由器之间进行名字路由通告等的通信开销，故而命名粒度对路由器的查表转发效率会造成非常巨大的影响；同时，由于一个请求仅包含一个内容名字（也就是说只请求一个内容块），因而有多少个内容名字，就需要多少个内容请求，相应的命名粒度会影响网络中用户需要发送的请求数量，进而影响ICN 的总体转发效率。然而目前针对命名粒度对ICN 效率的研究还主要集中在命名粒度对缓存机制影响上，本文则尝试从命名粒度对ICN 转发效率的影响进行探究。

因此，本文旨在回答以下四个问题：

（1）命名粒度如何影响名字数量：通过计算分析知道随着命名粒度呈倍数上升，在粒度较小时名字数量呈倍数下降，在粒度较大时名字数量下降趋势减缓并最终趋于文件数量；

（2）命名粒度如何影响请求数量：由分析可知请求数量随命名粒度变化的趋势和名字数量随命名粒度变化的趋势是一致的；

（3）命名粒度如何影响路由表规模：对于层次化命名，其路由表规模仅和文件数量和聚合度相关；对于扁平化命名，其路由表规模的变化趋势和由命名粒度变化所导致的名字数量的变化趋势一致；

（4）命名粒度如何影响查表效率：命名粒度主要通过影响路由表规模来影响单次查表效率，通过影响单次查表效率和请求数量来影响综合查表效率。

本文组织结构如下：第1 节简述相关工作；第2 节探索命名粒度对名字数量的影响；第3 节探索命名粒度对请求数量的影响；第4 节探索命名粒度对路由表大小的影响；第5 节探索命名粒度对路由查表效率的影响。

1 相关工作

目前信息中心网络主要有两种命名方式，一种是以CCN/NDN 为代表的层次化命名方式[3-5]，这种命名给每个内容单元赋予了URL 一样具有语义和可聚合性的名字，有利于网络规模扩展；另一种是以DONA 为代表的扁平化命名方式[6]，这种命名给每个内容单元赋予了不可读且不可聚合的扁平化名字，该名字一般由发布者公钥的哈希值和内容的哈希值组合而成，具有自验证和信息隐藏等特点。关于命名方案，目前主流的信息中心网络主要对网络中的命名方式作了相关规定，但是对命名粒度则只是给一个大概的取值范围，而没有阐述这样取值的原因，也没有深入探究命名粒度变化可能对网络效率造成的影响。

目前关于命名粒度如何影响信息中心网络效率的研究总体还是比较稀缺，且现有研究基本集中在命名粒度如何对网络缓存性能造成影响上[7-8]。本文则尝试采取一种新的研究思路来探究命名粒度对信息中心网络性能的影响，从命名粒度与名字数量、请求数量、路由查表效率这三者的关系来进行探究。

2 命名粒度对名字数量的影响

由于命名粒度通过改变名字规模来影响路由转发效率，因此在分析请求次数、条目规模和路由转发效率之间的关系之前，需要先简要分析命名粒度和名字规模之间的变化关系。令n表示网络中的文件数量，Si表示第i（1≤i≤n）个文件的大小，表示网络中所有文件的大小之和，s表示内容命名粒度，则网络中的名字数量N 可以用式（1）给出：

由于名字数量受到每个文件大小的影响，因此还需要考虑网络中文件大小的分布情况，即不同的文件大小在网络中所占的比例。参考现有工作中关于网络内容分发状态的研究[9-10]以及网络仿真实验的模型与参数设置[11-12]，可以认为网络内容的大小分布总体遵循帕累托分布（Pareto distribution），即一种典型的重尾分布。假设随机变量X服从帕累托分布，则X的概率分布如下式（2）所示：

其中xmin＞0 是X的最小值，是取值为正的参数，x表示任意X的取值。

假设网络中有1 000 000 个待分发文件，其大小分布遵循上述的帕累托分布，取分布模型参数α=1.1，xmin=(133)KB[12]，由帕累托分布模型随机生成的随机文件大小序列的分布情况的互补累积分布函数（CCDF）如图3所示，其中横坐标为文件大小，单位为KB，纵坐标为当前网络中随机取一个文件的大小大于该文件大小的概率值。

由图3可以看出生成的随机文件大小序列呈现典型的重尾特征。在根据帕累托分布生成分布如上图所示的随机文件大小序列时，假设现在的命名粒度为4 KB，则我们根据（1）式计算可得总名字数量为353 868 223。后面的实验将采用同样的计算方法，在不同的条件下根据帕累托分布生成一定数量的文件大小序列，然后在不同粒度下进行计算并将结果进行汇总分析。为了方便下文分析，这里引入平均名字数量K，该值的计算如公式（3）所示：

式中Ni表示当命名粒度为i时网络的总名字数量，n表示文件数量，则Ki表示命名粒度为i时网络中每个文件所拥有的平均名字数量。拿上面的例子来说，可用公式（3）计算其K值为353.868。这里引用K值来衡量名字规模大小，是因为分析名字数量规模时我们相较于确切的绝对名字数量更关心名字数量的变化趋势，因此相对数量K是一个比较好的选择。

下面将利用根据帕累托分布生成的随机文件大小序列来探究命名粒度和名字规模之间的关系，为了能更全面地评估命名粒度对名字数量的影响，文本假设命名粒度取[2, 4, 8, 16, 32, 64, 128, 256, 512,1024, 2048, 4096, 8192]，单位为KB，并采用（1）式计算名字数量。下面设置了三组不同条件的对照实验，每组实验将控制不同的变量来讨论不同网络变化情况下命名粒度和名字规模间的数量变化趋势，每组实验将测试三次并取均值：

图3 关于文件大小的CCDF 图Fig.3 CCDF of file size

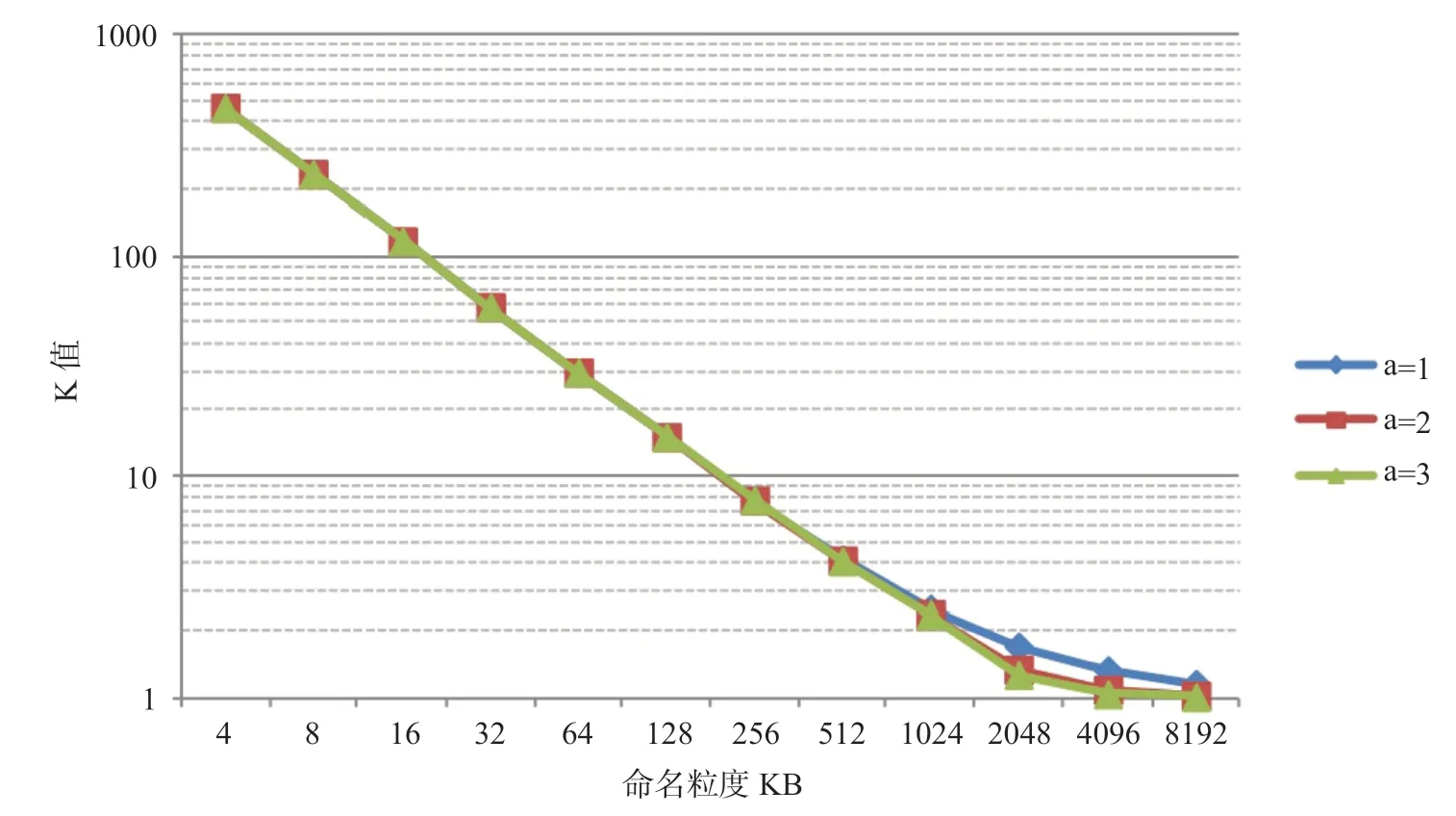
图4 情况一下不同帕累托分布参数下的K 值Fig.4 K value under different Pareto distribution parameters in case 1

（1）保持文件数量n和文件内容总大小S不变，采用不同的α和xmin值。它表示维持网络总体量不变，但是通过改变帕累托参数来改变文件大小分布情况。这里设置文件数量n为1 000 000，参数α分别设置为1， 2， 3，通过计算参数的取值来维持文件内容总大小S不变。得到的K值如图4所示，其中横坐标为命名粒度，纵坐标为该粒度下的K值，纵坐标采用以10 为底的对数刻度。

由图4可以清晰地看到，在命名粒度呈倍数增加的时候网络中的K值会明显下降，这和前文的理论分析结论是吻合的。且通过对比实验结果，可以得知不同α值下K值的曲线是重合的，这说明在控制文件数量及内容总大小不变的情况下，不同α取值情况下的K值基本相同，变化趋势也是基本一致的，以此可以看出文件大小分布情况对K值基本没有影响。分析K值变化趋势可以发现在命名粒度呈二的幂次增长时，在粒度较小时K值也是成幂次下降的，但是在命名粒度增长到比较大的时候K值的下降趋势减少并趋于不变，这是因为当命名粒度较大时比该粒度小的文件本来就不能被进一步分片，因此粒度再变大也不会显著让K值减小；而当命名粒度增长至大于当前所有文件时，即使命名粒度再变大文件也不会产生新的分片，故此时K值会等于文件数量而不再下降。

（2）控制参数α和参数xmin相同，采用不同的文件数量n和文件内容总大小S。它表示维持文件大小分布情况不变，通过增减文件数量来扩大或收缩网络总体量。这里参数α设置为1，xmin设置为133，文件数量n分别设为1 000 000,10 000 000,50 000 000。其中由于没有进行文件内容总大小控制，因此会有一定的随机性，故这里每组试验均进行三次实验并取平均值。得到的K值如图5所示，其中横坐标为命名粒度，纵坐标为该粒度下的K值，纵坐标采用以10 为底的对数刻度。

如图5所示，同样可以发现在命名粒度呈倍数增加的时候网络中的K值会成倍数的下降，其变化趋势与前述情况（1）基本一致。且对比实验结果可以得知不同文件数量下K值的曲线是基本重合的，这说明在控制拓扑生成参数α值和xmin值不变的情况下，不同文件数量规模下的K值基本相同，变化趋势也是基本一致的，由此可以看出文件数量规模虽然会影响总名字数量的大小，但对相对数量K的取值基本没有影响。

（3）控制文件内容总大小S和参数α相同，采用不同的文件数量n和xmin值。它表示维持网络总体量不变，文件大小分布基本不变，但是通过参数xmin来改变文件的平均大小。这里参数α设置为1，文件数量分别设为1 000 000,10 000 000,50 000 000，通过计算参数xmin的取值来维持文件内容总大小S不变。得到的K值示意图如图6所示，其中横坐标为命名粒度，纵坐标为该粒度下的K值，纵坐标采用以10为底的对数刻度。

如图6所示，同样可以发现在命名粒度呈倍数增加时网络中的K值会成倍数的下降。但是和前述情况（2）不同的是，控制文件总内容大小与α不变的情况下，不同的文件数量取到的K值有较大差异，且文件数量越多则K值越小。这是因为在网络总大小不变时，文件数量越多意味着每个文件平均分到的内容就越小，因此每个文件平均拥有的名字数量（即K值）也越少。

由图6同时可以看出不同文件数量下K值随命名粒度变化的趋势和前述情况（1）（2）基本一致，不过随着文件数量变大，变化趋势曲线整体向左平移。这是因为当文件数量变大时文件平均大小变小，这会导致文件在前期粒度不大时就已经不能被进一步切分，从而使K值变化提前达到变化趋势后期的变化平缓期。

综合上述三种情况的实验结果，可以得出两个主要结论：（1）随着命名粒度呈倍数增加，在粒度较小时K值会呈相应倍数减少，而在命名粒度较大时则减速放缓并使K值最终趋于1，且在不同网络场景下这个K值变化的趋势都是成立的；（2）文件大小分布情况和总体网络规模对K值的影响都是非常小的，真正能显著影响K值的其实还是平均文件大小，这里可以粗略表述为总内容大小与文件数量的比值。

图5 情况二中不同文件数量时的K 值Fig.5 K value for different scales of files in case 2

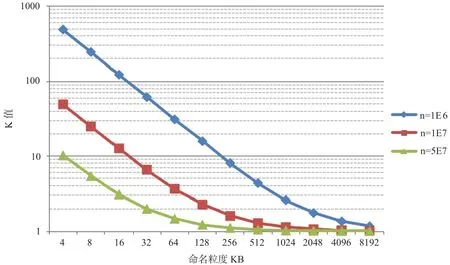
图6 情况三中不同文件数量时的K 值Fig.6 K value for different scales of files in case 3

3 命名粒度对请求数量的影响

如前所述，因为当接收方请求某个文件时，如果该文件在命名时被分割为若干部分，那接收方至少需要请求的数量等于该文件所拥有的名字数量。因为前述K 值的定义为网络中每个文件平均所拥有的名字数量，因此在这里可以将K 值看作是网络中获取一个文件平均需要的请求次数。那么依据第二部分的实验结论，这里同样可以得出两个结论，一是随着命名粒度呈倍数上升，网络中平均请求数量呈倍数下降，且在粒度较大时下降幅度减缓，直至最后等于文件数量；二是文件分布情况和总体网络规模对网络平均请求次数的影响不大，网络平均文件大小才是影响平均请求次数的主要因素。

4 命名粒度对路由表规模大小的影响

接下来分析命名粒度变化对路由表规模大小变化的影响，由于这个影响很大程度上被命名方式所左右，因此我们将分别对层次化命名方式和扁平化命名方式进行讨论。

4.1 层次化命名方式

层次化命名对命名空间内部各个部分赋予了语义也添加了相应的可选约束，这种方式虽然可能会暴露一定的信息，但是可以利用语义与约束来进行名字聚合——对于层次化命名方式而言，由于层次化的名字空间中的很多名字都共享相同的前缀，故路由器可以利用该特点对大量路由条目进行名字聚合，这样会导致该命名方式下的路由表具有两个特点：

（1）路由表中的条目数量远远小于其所覆盖的名字空间的名字数量，例如AS65000 的路由条目报告[13]所称的目前核心路由表项数量是827009，其覆盖的总名字空间大小为2853207852，计算名字聚合的优化比例为：

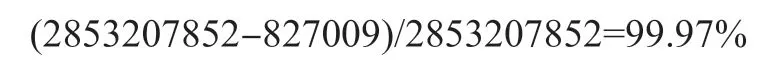
该结果足以说明层次化命名下名字聚合的效率是非常高的。

（2）路由表可以屏蔽由于命名粒度变化导致的名字数量变化对核心路由表规模的影响，比如对于某视频切片可能拥有名字为buaa.edu.cn/video/20200326/s1，而其对应的路由表项可能为buaa.edu.cn/video/20200326，现在由于命名粒度变化导致该切片被继续分割为16 个小块进行命名，其名字变为buaa.edu.cn/video/20200326/s1/a1～buaa.edu.cn/video/20200326/s1/a16，名字数量变为原来16 倍，但是为其转发的路由表则可以维持buaa.edu.cn/video/20200326 一个表项不变。

以上例子说明在层次化的命名方式下，命名粒度变化所导致的名字数量的变化对路由表项规模的影响是非常小的，特别是在我们比较关注的、名字聚合度非常高的核心网中，这种影响完全是可以忽略的。因此，后面的分析将以网络总文件数量n作为其路由表最大条目数量，在此基础上引入聚合度λ，然后将二者的乘积λn作为聚合后的条目数量，这里λ可以取0.1、0.01、0.001 等。

4.2 扁平化命名方式

扁平化命名主要指命名空间内部各个部分的取值是没有语义和相互约束的，这意味着很难利用语义进行名字聚合，同时也因为语义的缺失而提高了安全性。由于扁平化命名方式缺乏层次化命名方式的名字聚合手段，因此在该命名方式下，路由表中的条目数量等于其所覆盖的名字空间的名字数量，而且不能屏蔽命名粒度变化所导致的名字数量的变化对路由表项规模的影响。因此可以认为扁平化命名方式下的条目数量正比于名字数量，且条目数量的变化趋势和由命名粒度变化所导致的名字数量的变化趋势是一致的。

利用前面第2 节的分析结果可以得到名字数量关于命名粒度的数量变化趋势，而且数据分析表明这个数量变化趋势在不同网络条件下都是基本成立的，其曲线仅随着平均文件大小左右平移。由此就可以利用该数量变化趋势得到扁平化命名方式下在不同网络环境都较为可信的条目数量。

综上分析，取文件数量n=1 000 000，分布模型参数α=1.1，xmin=(133)KB 得到名字数量后再经过适当放缩，就可以得到扁平化命名方式下的条目数量，对其文件数量同样放缩后乘以不同的聚合度λ 就可以得到层次化命名方式下的条目数量，最终汇总得到的不同命名方式下条目数量示意图到图7所示，其中横坐标为命名粒度，单位为KB，纵坐标为条目数量，纵坐标采用以10 为底的对数刻度。在扁平化命名方式下，路由表条目数量比文件数量多，且总体变化趋势为随着命名粒度增大而减少；在层次化命名方式下，路由表条目数量比文件数量少，其具体大小取决于聚合度的大小。

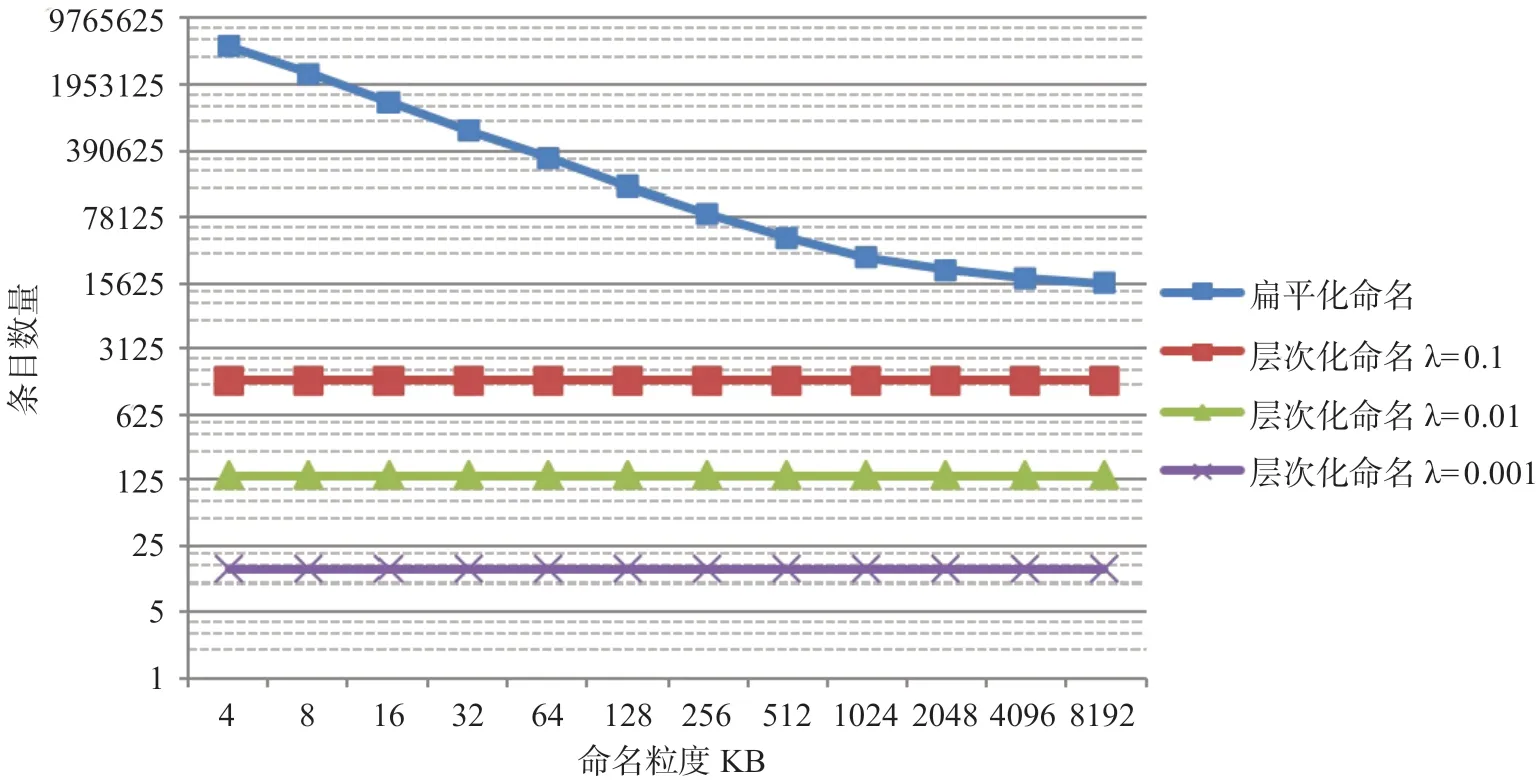
图7 不同命名方式下的条目数量Fig.7 Number of entries under different naming methods

5 命名粒度对查找效率的影响

综合上述分析，命名粒度主要是通过改变网络中的名字数量来影响文件平均请求数量以及路由表规模，进而影响路由查表效率的。下面将两部分讨论命名粒度对查找效率的影响，第一部分将探究单次路由查找的效率，第二部分将探究总查找效率。

5.1 单次路由查找效率

要考虑命名粒度对单次路由查表效率的影响，就要考虑路由查表算法在其中的作用。路由查表算法主要指的是路由器用来组织、储存路由表项并在包转发时用来进行匹配查询的算法。因为命名粒度变化主要是通过影响路由条目规模来影响路由查表效率的，而不同的路由查表算法效率和条目规模之间的效率关系是不一样的，这种效率关系决定了路由算法对条目规模变化的耐受程度，而且不同命名方式下路由查找算法和条目规模的效率关系也可能是不同的，因此是不同命名方式下粒度变化影响路由查表效率的关键因素。

本部分将在扁平化和层次化这两种命名方式下，分别在不同的条目数量规模下测试不同路由查表算法的查表效率，以此来探寻不同命名方式下不同路由查表算法的效率随表项规模变化的数量关系，进而找到不同命名方式下粒度对查表效率的影响。因此，本实验主要考虑条目数量、命名方式和路由查表算法这三方面：

（1）条目数量方面，由前面分析，可以直接利用第四小节内容命名粒度和条目数量规模的数量关系的探究结果，即取图7不同命名方式下的条目规模作为测试时的条目规模。

（2）命名方式方面，除了条目数量上的区别，实验中不同的命名方式主要体现在生成测试数据集时使用的不同的生成方法，扁平化的命名方式直接每个字节随机填入即可，而层次化的命名方式则需要在生成测试数据集的时候用多层循环来嵌套生成测试数据，以此用递进的公共前缀来保证命名空间之间的层次约束性，这里需要注意的是在生成多个大小规模的测试数据集时要保证不同层间比例的一致性。

（3）路由查表算法方面，这里拟对在路由查表中较具有代表性的Hash 查表算法、ByteTrie 查表算法[14]和NPT[15]算法进行条目规模与查表效率的测试。Hash 查表算法采用Hash 表的方式存储和查找路由条目，为了使结果更具典型性，这里采取了经典的拉链哈希法；ByteTrie 算法采用多叉树结构存储和查找路由条目，其中还对单子树节点进行了树结构的压缩优化；NPT 算法则是利用一个多叉四层结构树来存储和查找路由条目，层级之间用Hash 方法来进行跳转，主要针对层次化命名方式。

测试中生成测试数据和测试查表效率的程序均采用C 语言实现，实验环境为笔记本电脑，处理器为Intel Core i7-4510U 四核CPU，内存为8GB。在实验时根据命名方式的不同随机生成并插入对应数量的路由条目，然后测试不同路由查表算法的查表耗时，其中每组查表次数为1000 万次，反复进行3组测试取均值。

测试结果如图8和图9所示。图8的横坐标是内容命名粒度大小，纵坐标是查表时间，单位为毫秒，且测试中的层次化命名的聚合度λ 取0.1。由图8的实验结果可以得出不同内容命名粒度下不同查表算法的单次查表耗时t，并可以得到结论及分析如下：

（1）在查表算法效率方面，Hash 算法> Trie 算法> NPT 算法，这是因为Hash 算法因查找时只需进行一次哈希运算而非常高效，而Trie 算法由于引入了相对灵活的树结构压缩优化机制而比严格进行四层哈希跳转的NPT 算法更为高效。

（2）同一内容命名粒度下，就同一查表算法而言，层次化命名方式下的路由查表效率比扁平化命名方式高，其中Trie 算法下两种命名方式的效率差别是最大的，NPT 算法的效率差别也很显著，这不仅因为层次化命名方式可以进行路由聚合优化缩减表项数量，还因为该方式下命名空间中各部分取值具有一定的逻辑约束性，因此拥有公共前缀的路由条目的数量远大于完全随机的扁平化命名方式，故对Trie 算法来说显著减少了查找空间（即查找深度和平均子分支），大大提高了路由查找效率，而对NPT 算法来说则因为大量存在的公共前缀减少了查找过程在上层哈希碰撞的概率，因此也在一定程度上提高了其路由查表效率。

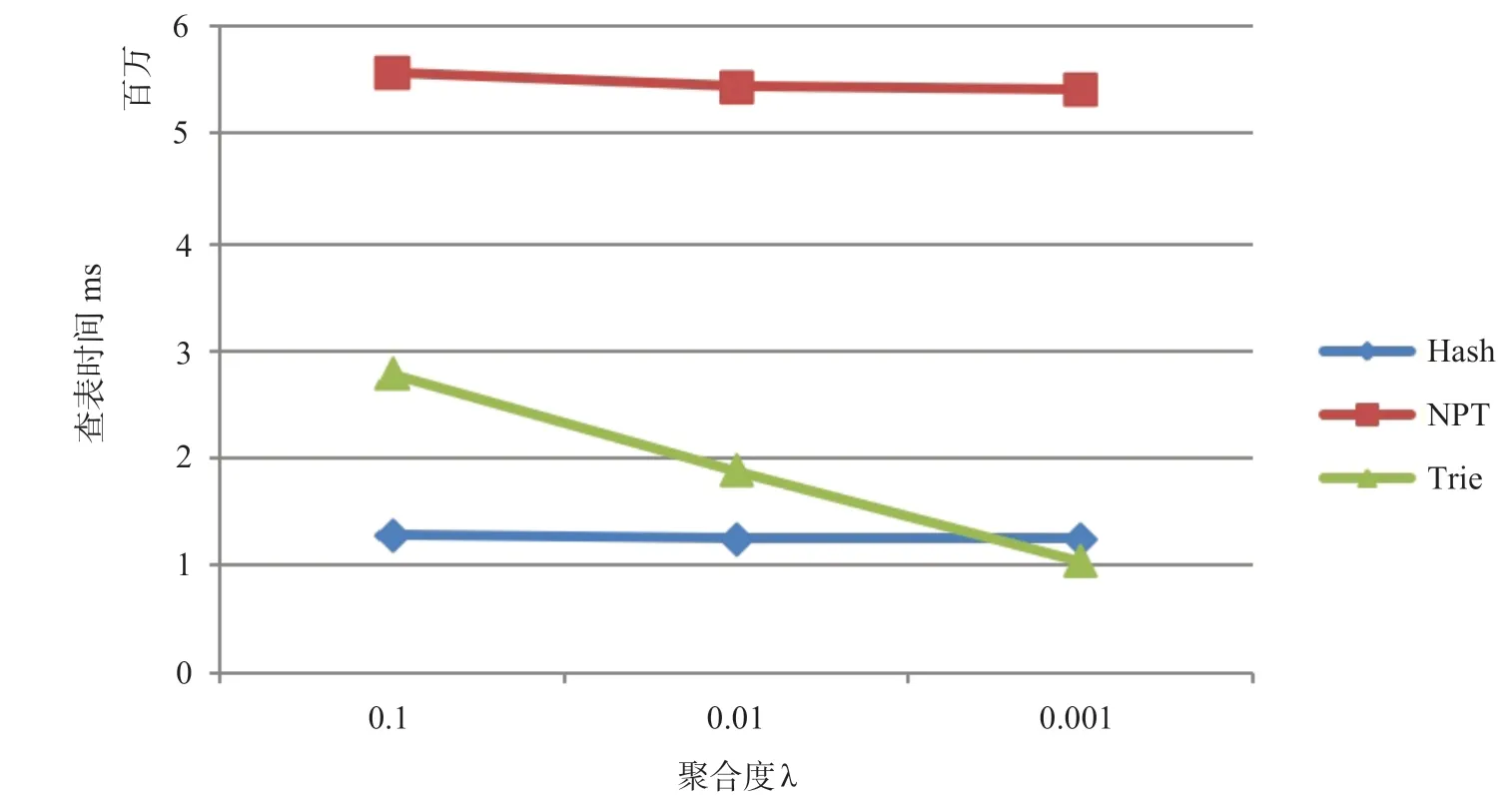
图9 层次命名下不同聚合度的查表效率Fig.9 Efficiency of looking up tables with different degrees of aggregation under hierarchical naming

（3）在内容命名粒度不断增大时，扁平化命名方式下所有路由查表算法的效率都在提高，其中以Trie 算法查表效率提高的效果最为明显，NPT 算法和Hash 算法则几乎没有什么变化，这是因为Trie 算法的查找时间复杂度大概是O（log(n)），因此对内容命名粒度改变引起的路由条目规模变化还是相对敏感的，而Hash 算法和NPT 算法的查表时间复杂度都是近似于O（1），因此这两种算法的路由查表效率对路由条目规模的变化不是很敏感，当然由路由条目减少而导致的Hash 碰撞减少还是会使查表效率有非常细微的提升的。

图9的横坐标是层次命名方式下的聚合度λ，纵坐标是查表时间，单位为毫秒。图9的实验结果可以得出层次化命名下不同聚合度的查表耗时情况，分析可知三种查表算法的效率都随着聚合度的减小而上升，其中Trie 算法的效率提升是最明显的，且在聚合度λ 较高时Trie 算法的效率甚至会高于Hash 算法。

5.2 总查找效率

在得出单次查表效率以后，想要得到综合查表效率这里还需要考虑接收方想请求一个文件所需要发送请求包的次数，因为内容命名粒度除了影响单次查表效率以外，还会直接影响请求一个文件所需的平均请求次数。这里根据第3 节的分析结果，可以将前面引入的K 值作为网络中请求一个文件平均需要的请求次数。因为在不同网络环境下K值的变化趋势都是一致的，故这里采用图4的K 值数据作为随命名粒度变化的平均请求次数。

综合不同内容命名方式、各个内容命名粒度下的单次查表耗时和平均请求数量，可以计算得到综合查表耗时。计算方法如式（4）所示，其中Ki表示内容命名粒度为i时的平均请求数量，ti表示粒度为i时的单次转发效率，Ti即为内容命名粒度为i时的综合查表耗时。

综上所述，利用前述第2 节关于K值的计算数据和本节关于单次查表效率的测试数据，再综合式（4）即可以计算得到综合查表耗时结果如图10 所示，图中横坐标为内容命名粒度，纵坐标为综合查表耗时，单位为毫秒，纵坐标采用以10 为底的对数刻度，层次化命名方式的聚合度λ取0.1。由图10 可以得到相关结论及分析如下所示：

（1）分析算法之间的综合查表效率同样可以看出Hash 算法 > Trie 算法 > NPT 算法；

（2）同一内容命名粒度下，就同一算法来而言，层次化命名方式的综合查表耗时同样小于扁平化命名方式；

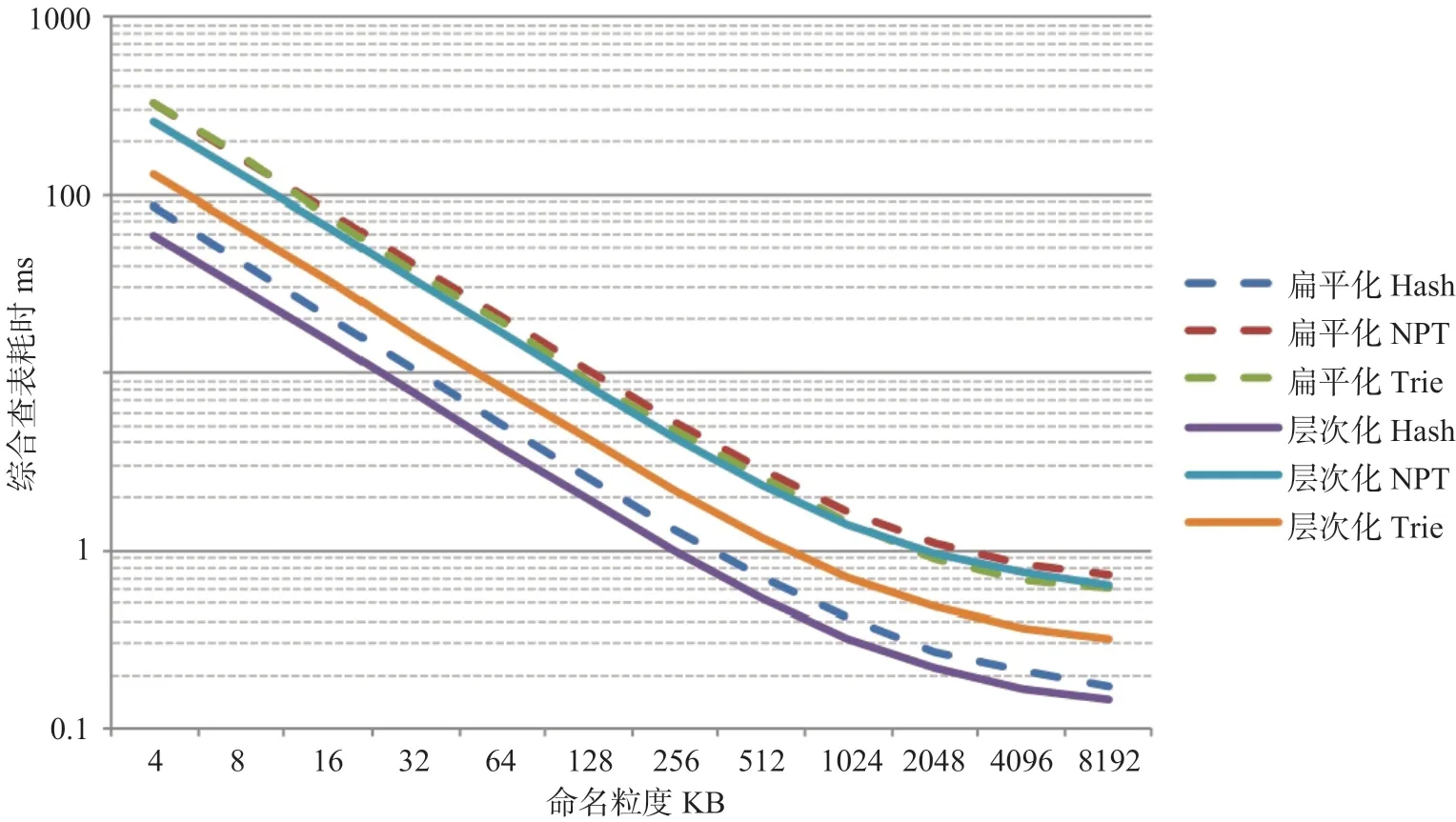
图10 综合查表耗时结果Fig.10 Time consuming result of comprehensive table lookup

（3）随着内容命名粒度变大，综合查表耗时都会变小，即请求一个文件平均所需的查表耗时更小，这是因为如前分析所示随着粒度变大平均查表耗时和平均请求数量都在减小，故总体而言效率自然变高，而且变化的幅度比单次查表耗时更明显；

（4）不同命名方式、不同查表算法间由内容命名粒度变化而引起的综合查表耗时变化的幅度差异不大，这是因为现在平均请求数量变化远大于体现命名方式、查表算法特点的平均查表耗时变化，因此平均请求数量成为综合查表耗时变化幅度中的主要影响因素。

6 展望与下一步工作

本文通过逐步推进分析探究了信息中心网络中不同命名方式下内容命名粒度对路由查表效率的影响，先从内容命名粒度对名字数量的影响出发，在找到名字数量关于命名粒度变化的数量规律后再据此分析网络请求数量和不同命名方式下路由表的条目规模，最后在分析结果的基础之上以实验来具体测试、分析了不同命名方式下条目数量规模和路由查表效率之间的关系，进而揭示了信息中心网络中不同命名方式下内容命名粒度对路由查表效率的影响。但是，本文的工作主要还是基于理论分析和本地测试，而缺乏实际网络测试结果的支撑。因此，在下一步工作中，将在本文实验分析的基础上，利用软件路由技术在服务器集群上搭建信息中心网络测试环境，然后在真实的物理场景下进行大规模的路由转发测试来得到更可靠、详细的实验数据来对本文结果进行进一步的物理验证。

利益冲突声明

所有作者声明不存在利益冲突关系。