Taylor多项式模型在实验教学中的应用

文丽敏 高国明 白春华

摘要：在学生教育中，把理论教学和实践教学有机地融合起来，从而使学生较为轻松有效地学习。《地磁地电观测》实验是地球物理专业的一门实践课程，包括模拟实验及仪器实验部分，而模拟实验主要是将已学的编程语言应用到专业数据处理中，而地磁数据处理是以后学生进行科研的基础。地磁场模型是研究地磁场空间分布与时间变化规律的主要手段，包括全球和局部地区两类模型，Taylor多项式级数法是地磁场模型中在局部磁场分析中广泛采用的方法，该模型的最大优点是计算简单，使用方便。我们设计利用Taylor多项式模型计算中国地区地磁场长期变化的实验，让学生掌握建立地磁场Taylor多项式模型的原理和方法，编程计算中国地区地磁场的长期变化，做出地磁场X，Y和Z分量的长期变化图。

关键词：TaVlor多项式;地磁场模型;地磁场分量;实验教学

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2020）29-0156-04

现阶段的学生教育中，在理论教学的基础上，强调实践教学。而把理论教学和实践教学有机地融合起来，理论直接指导实践，实践中又更好地领会理论，从而使学生较为轻松有效地学习[1]。地球物理专业通过定量的物理方法研究地球，对地球的物理场分布和变化进行观测，研究范围包括地球的地壳、地幔、地核和大气层。因此本专业开设了《地磁地电观测》实验课，是一门重要的专业基础课程。相对于其他专业课，该课程是一门理论与实验并重的专业基础课[2]，其以地磁学和地电学等专业课程为理论基础，学生通过模拟编程和使用仪器进行实际观测，熟悉地球物理中的地磁场和地电场的数据处理和各种常规仪器的使用方法。因此我们在设计学生的实验时，既要考虑到学生已经具有的专业知识，又要在此基础上给学生一定的实习空间。Taylor多项式模型实验就是为了锻炼学生的实际动手能力，将理论与实际数据分析结合起来，提高学生的创新能力而设计的实验。通过此实验，将Taylor多项式模型应用于中国及邻区地磁场分量的计算，使学生掌握了Taylor多项式模型的原理及方法，为以后学习中要进行的数据分析计算打下基础。

1 地磁场建模的方法

地磁场模型是研究地磁场空间分布与时间变化规律的主要手段，包括全球和局部地区两类模型[3]。现在应用的全球地磁场模型是国际地磁参考场（IGRF），由国际地磁学与高空大气物理学协会采用来自卫星磁测的地磁数据研究得到的全球球形模型，该模型每五年为一个间隔[4]。IGRF描述的地球磁场的时空分布尺度较大，因此对于局部的小尺度磁异常研究，其精度就不能满足需要，因此，有必要建立局部地区的地磁场模型。局部磁场分析中广泛采用的方法有Taylor多项式级数法、曲面样条函数方法、矩谐分析方法、球冠谐分析方法等[5-6]。矩谐分析和球冠谐分析方法基于高斯磁位理论，满足位理论的物理限制，所获得的模型物理意义明确，表示位场的三维结构比较方便。因此地磁场的三维结构及其变化过程可以利用这类模型进行理论分析与探讨。曲面样条函数和Taylor多项式等方法在地磁场建模中也得到了广泛应用，该方法分别对地磁场的独立分量在某一空间区域内的分布进行拟合[7]。

我们在进行地磁场建模时，选择建模方法的依据主要有物理的合理性、计算的稳定性、级数的收敛性、计算的准确性、功能的多样性、使用的方便性等[8]，这些从物理意义、计算及使用等方面提出了要求，成为我们建模的关键。

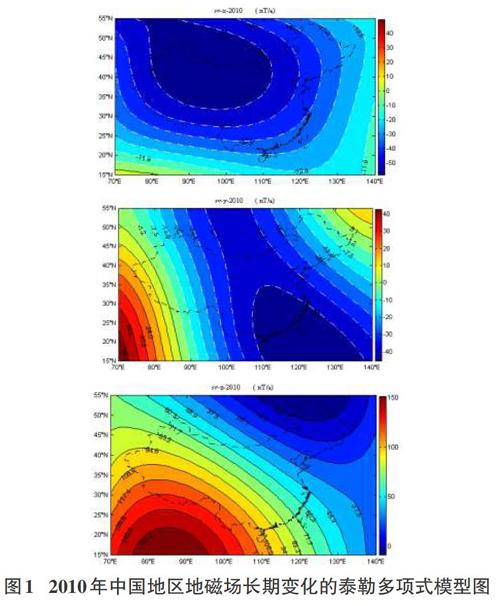
Taylor多项式模型的最大优点是计算简单，使用方便，因此我们设计实验就是利用Taylor多项式模型计算中国地区地磁场长期变化，通过此实验让学生掌握建立地磁场Taylor多项式模型的原理和方法，编程计算中国地区地磁场的长期变化，做出地磁场X，Y，和Z分量的长期变化图。

2 Taylor多项式原理

Taylor多项式是以1715年发表了泰勒公式的英国数学家布鲁克·泰勒的名字来命名的，是一个用函数在某点的信息描述其附近取值的公式，广泛地应用到数学、统计学、社会科学等各个领域[9]。

用Taylor多项式对地磁场的不同分量进行拟合，其数学描述如下：

A和B相当于已知，我们用最小二乘法求解出X，得到待定系数a00，a10，a11，…，a33，即X已经求出。再利用X及A既可以求出不同经纬度點的地磁场分量。本实验要求求出中国地区地磁场X、Y，和Z分量，并做出他们的长期变化图。

3 用Taylor多项式建立地磁场模型需要注意的问题

3.1 计算区域及计算中心的选取

选择计算区域为矩形区域，本实验为5° - 55°N和70° -140°E。计算中心即为展开原点，特勒多项式展开原点（φ0，λ0）可在计算区域的中心附近，取整度，以使计算更为方便，本实验为（36°N，105°E）。展开原点的位置的选择可以变化，但是我们计算得到的系数也会相应地发生变化，但是这并不影响地磁场的拟合效果。

3.2 模型资料的选取

在本实验中我们选取中国地区2010年地磁观测数据X、Y和Z分量TaYlor多项式模型。

3.3 截断阶数N的确定

Taylor多项式模型的截断阶数N的选择尤其重要，因为N对模型计算结果的影响较大。N太高不仅会增加计算的难度，还会有边界效应，产生畸变;N太低模型的空间分辨率差，不能清楚地表示地磁场的分布。如何确定N是模型的关键，主要根据区域模型计算的均方偏差确定N。我们计算得到的均方偏差与全球模型的均方偏差进行对比，不要比后者大;同时随截N的增加，基本趋于稳定。通过实际计算结果，我们发现选用N=5更为合适[7]。

4 Taylor多项式模型在实验中的应用

1）根据以上原理编制程序cal_tarlor.m，计算中国地区地磁场长期变化Taylor多项式模型系数。

caLtarlor.m

clear all

year=2010;

gh=strcat（ ' sv ' ，int2str（year）， ' .dat 7）;

d=load（gh）;

wd=d（：，2）-36;

jd=d（：，l）-105;

k=2;

xl=[jd jd.^2 jd.^3 jd.^4 jd.^5];

x2=[wd wd.*j d wd.*j d.^2 wd.*j d.^3 wd.*j d.^4];

x6=wd.^5;

xx=[ones（size（wd》 xl x2 x3 x4 x5 x6];

for i=1：7

a=xx＼y;

end

ghh=strcat（ 'xishu_tarlor' ，int2str（year）， ' .dat '）;

dlmwrite（ghh，hh， ' delimiter'， '＼t' ， 'precision'， ' %15.lOf'）;

clear hh;

2）计算 X， Y， Z三分Y量磁场的长期变化 ，运行程序 geom_tldxs.m进行计算 。

geom_tldxs.m

clear

year=2010;

gh=strc at （ 'xishu_tarlor ' ，int2str（year）， ' .dat '）;

aa=load（gh）;

wd=5：5：55;

jd=70：5：140;

f0=36.0;

lt0=105;

for ii=1：7

for il=l：length（wd）

x=（wd（il）-f0）;

for jl=l：length（jd）

y=（jd（jl）-lt0）;

hh=O;n=0;

for i=0：5

for j=0：5-i

hh=hh+a（n）*x^i*y^j;

end

end

f（ii）.dd（il，jl）=hh;

end

end

end

fx=strc at （ ' x_sv r ，int2str（year） ， r .dat'）;

fy=strcat（' y_sv ' ，int2str（year） ， ' .dat'）;

fz=strcat（ r Z_Sy r ，int2str（year）， r .dat '）;

dlmwrite （fx，f（l）.dd， 'delimiter'， '＼t '， r precision'， ' %10.5f'）

dlmwrite（fy，f（2）.dd，'delimiter'， '＼t r ， r precision'， r %10.5f'）

dlmwrite （fz，f（3）.dd， ' delimiter' ， '＼t' ， ' precision' ， ' 0-10 10.5f'）

a=size（f（l）.dd）;

phi=jd;

wd=wd;

wdd=length（phi）;

tx=zeros（l，a（l）*a（2》;

ty=zeros（l，a（l）*a（2》;

tz=zeros（l，a（l）*a（2》;

for i=l：a（l）

end

for i= 1 ：length（wd）

jwdd《（i-l）*wdd+l）：（i*wdd），2）=wd（i）*ones（wdd，l）;

jwdd《（i-l）*wdd+l）：（i*wdd），l）=phi';

end

X2=Dwdd tx'];

Y2=Dwdd ty'];

22=[jwdd tz'];

%據数

file=strcat（' x-sv '，int2str（year），' s.dat '）;

dlmwrite（f'ile，X2， 'delimiter'， '＼t '， ' precision '， r %15.5f'）;

file=strcat（ 'y_Sy '，int2str（year），' s.dat ' ）;

dlmwrite（file，Y2， 'delimiter'，'＼t'， 'precision'， r %15.5f'）;

file=strcat（ ' z_sv '，int2str（year）， ' s.dat ' ）;

dlmwrite （file，22， ' delimiter' ， '＼t' ， ' precision ' ， ' %15.5f '）;

3）运行程序 sv_zuotu.m，做出中国地区地磁场长期变化 WJTaylor多项式模型图 。

sv_zuotu.m

clear

fl=['Xr 'yr 'Z'l;

FLk['Xr 'yr 'Z'];

x=70：140;

y=5：55;

year=2010;

for hg=1：7

file=strcat（fl （h g）， '_sv ' ，int2str（year）， ' .dat '）;

z=load（file）;

x=70：140;

y=5：55;

[cc，hhl=contourf（x，y，z，14， r LineStyle'， 'none'）;

colorbar（'location'， 'EastOutside'， 'FontSize'， 7.5， 'Position'，[0.915 0.208 0.019 0.616l， 'FontWeight '， 'bold '， 'Fontname'， 'timesnew romanr1.

hold on

h_text=clabel（cc，hh， r LabeISpacingr ，300， r FontSize ' ，6.5）;

for kkl=l ：length（h_text）

set（h_text（kkl）， 'string' ， sprintf（r % 2.lf'， get（h_text（kkl）， 'user-

end

h=contourc（x，y，z，14）;

dnn=l;dn=0;

while dnn<=size（h，2）

dnn=dnn+h（2，dnn）;

dnn=dnn+l;

dn=dn+l;

end

kk=l;

for i=2：dn

kk=kk+h（2，kk）+l;

end

k2=1;

k=2;

for i=l：dn

k2=k2+h（2，k2）;

k2=k2+1;

k=k2+1;

if hy（i）<0

plot（x，y， ' w-.'， 'LineWidth'，0.5）

hold on

else

plot（x，y， 'k_ '， 'LineWidth'，0.5）

hold on

end

end

set（gca， r PlotBoxAspectRatio '，[1 0.6 1]）;

set（gca， 'LineWidth'，l）;

set（gca， 'FontSize'，7.5）;

set（gca， 'XLim'，[70 140]， 'YLim ' ，[15 55]）

set（gca， 'XTick'，[70：10：140D;

set（gca， 'YTick'，[15：5：55]）;

set（gca， 'XTickLabel'，{'700E'，'800E'，'900E'，'IOOoE'，'1100E'，'1200E'，'1300E'，'1400E'D

set（gca， 'YTickLabel'， { r 150N'， '200N'， '250N'， '300N'， '350N '， r400N '，'450N '，'500N '， '550N'}）

if hg<=5

ghhh=strcat（ ' sv- ' ，FLL（hg），L '，int2str（year）， '

（ nT/a） '）;

else

ghhh=strcat（' sv- ' ，FLL（hg）， ' - '，int2str（year）， '

（ ＼circ/a） '）;

end

title（ghhh， 'FontSize'，7.5， r LineStyle'， 'none '， 'Fontname '， 'timesnew roman1

hold on

dat=load（r data_china_ditu.dat '）;

plot（dat（：，l），dat（：，2），'k-.' ， ' LineWidth'，0.5）

hold off

set（gcf， 'PaperPositionMode （ ，7manual'， r PaperUnits '， 'centime_

'PaperPosition'，[1 1 7.48 5.625D;

set（gca， 'FontSize' ，7.5， ' FontName '， 'Times New Roman 7）;

ghh=strcat（' sv- '，fl（hg）， ' _ '，int2str（year）， ' .tiff '）;

print（'-dtiff '，'_r600'，[ghh '.tiff'l）;

End

通过此实验，将Taylor多项式模型应用于中国及邻区地磁场分量的计算，使学生掌握了Taylor多项式模型的原理及方法，为以后学习中要进行的数据分析计算打下基础。

参考文献：

[1]王典，刘财，刘洋，等.基于教学实习的地震资料解释课程“理实一体化”教学研究[J].教育现代化，2018，5（31）：73-74.

[2]朱锐，蔡敦波，鲁统伟，等.数据结构理论与实验混合教学方法的探索[J].教育现代化，2017，4（50）：175-176.

[3]柳士俊周小刚孙涵安振昌，用于区域地磁场模型计算的三维Taylor多项式方法[J].地球物理学进展，2011，26（4）：1165-1174.

[4]王明，莫长涛，康崇，等.超小尺度地磁场泰勒多项式建模方法[J].哈尔滨商业大学学报（自然科学版），2014，30（3）：323-326。

[5]乔玉坤，王仕成，张金生，等.泰勒多项式拟合法在区域地磁场建模中的应用研究[J]工程地球物理学报，2008，5（3）：294-298.

[6]徐文耀，地磁学[M].北京：地震出版社，2003.

[7]顧左文，安振昌，高金田，等.2003年中国及邻区地磁场模型的计算与分析[J].地震学报，2006，28（2）：141-149，221.

[8]安振昌.地磁场多项式模型的分析与讨论[Jl.地球物理学报，2001，44（z1）：45-50.

[9]高文武.泰勒多项式的教学探讨[J]，宿州学院学报，2015，30（5）：119-121.

【通联编辑：唐一东】

作者简介：文丽敏（1975-），女，辽宁新民人，云南大学地球物理系讲师，工科硕士，研究方向：主要从事地磁学研究。