结合马氏距离的smote改进算法研究

徐湘君 刘波涛

摘要：传统的smote算法应用于非平衡数据集研究领域，它可以将少数类样本按照一定的条件进行扩充，以达到让非平衡数据集中少数类样本和多数类样本达到平衡这一目的。但是它在对于边界元素的选择生成数据的时候具有盲目性，使得生成的新的数据降低少数类样本的质量。针对这种情况，提出了将马氏距离结合SMOTE算法的改进算法Maha-smote，让生成的新元素更加靠近样本集中心，提高生成的数据集的总体质量。本文分别使用传统SMOTE、Pychon的sklearn库中的SMOTE算法以及Maha-smote算法对所选用的3个不平衡数据集进行过采样数据预处理然后使用决策树和高斯朴素贝叶斯GNB分类器对预处理后的数据集进行预测，选择F-Measure、AUC作为分类性能的评价指标，实验表明Maha-smote算法预处理的不平衡数据集的分类效果更好，证明了该算法的有效性。

关键词：非平衡数据集;上采样;SMOTE算法;马氏距离;边界样本

中图分类号：TP311 文献标识码：A

文章编号：1009-3044（2020）29-0028-04

1 引言

现如今常见的数据分类方法通常假设数据之间是平衡的，认为不同样本之间的数据数量是相差不多的，但是在我们的日常生活中还存在着许多非平衡的数据。例如医疗领域的病症方面的识别、金融方面的信用卡欺诈检测以及关于贷款方面的贷款检测[1]等。通常我们把数量大的类型成为多数类，数量少的类型成为少数类，在这些领域通常少数类与多数类之间的比例为1：10、1：100甚至为1：10000或更大[2]，这种情况下，传统的分类方法就不适用于非平衡的数据，因为他们通常会将少数类当作噪声处理掉，这样分类的话结果也不是我们想要的，在现实生活中也会带来不好的影响。

关于非平衡数据现如今有很多的研究，目前基本上是分为两个层面进行研究，分别为数据层面和算法层面。从数据层面出发就是改变数据之间的分布将不平衡的数据通过采样方法变成平衡的数据，N.V.Chawlac3]等人提出了最经典的SMOTE（Synthetic Minority Over-sampling TEchnique）过采样技术，Tor-res F Rc4]等人提出使用少数类k近邻样本的均值点来合成新样本的SMOTE-D算法，han hc5]等人提出来一种是自适应上采样方法Borderline-SMOTE。

从算法层面主要通过对算法进行优化来提高分类器的性能，例如徐丽丽[6]等人提出一种新的不平衡数据加权集成学习算法，主要是通过为各类别分配不同的权重将加权支持向量机模型WSVM（Weighted Support Vector Machine）与模糊聚类相结合。Nghe等[7]为降低不平衡数据集误分类的成本将采样技术与使用支持向量机SVM的代价敏感学习算法相结合。

本文主要从数据层面出发，对其中的上采样方法方面进行研究，提出一种基于马氏距离的SMOTE改进算法Maha-smote算法，以少数类样本为中心，选择k个近邻，通过比较元素与元素之间的马氏距离来判断生成的新元素应当更加靠近哪个元素，从而让生成的新元素更加的靠近整个集群的中心，而不会像传统的SMOTE算法一样，在边界上的离群点附近也会随机生成许多的新元素，从而使得新的平衡样本尽量少的产生质量较差的数据。

2 基础算法简介

2.1 SMOTE算法

SMOTE算法[1]的原理是通过相邻的两个少数类之间线性插值生成一个新元素，最终使得少数类与多数类数量达到一个数据之间的平衡。算法流程如下：

（1）对于少数类中每一个样本x，计算它的近邻的欧几里得距离，按照从小到大的顺序排序，将前k个近邻合并为k近邻集合;

（2）根据多数类和少数类样本的不平衡比例设置上采样倍率N，对于每一个少数类样本x，从其k近邻集合中随机选择几个样本，近邻样本为x。;

（3）对于每一个随机选出的近邻x。，分别与样本x按照合成新样本的公式构建新的样本。

Xnew=x+rand（0，1）×（xn-x）

SMOTE算法避免了随机过采样算法中造成分类器模型过拟合的问题，但是其在生成新样本的时候关于样本边界方面并没有进行考虑，因而在生成新样本还存在着些许的问题。

2.2马氏距离

马氏距离（Mahalanobis distance）是由印度统计学家马哈拉诺比斯提出的，它可以用来计算一个点与一个分布之间的距离。相对于欧氏距离，马氏距离对于样本的计算会考虑到特征的联系，但是却不会受到特征的尺度影响。

假设身高和体重，这两个变量拥有不同的单位标准，也就是有不同的尺度。比如身高用mm计算，而体重用kg计算，显然差lOmm的身高与差lOkg的体重是完全不同的。但在普通的欧氏距离计算中，这将会算作相同的差距。

上图中如果不考虑分布，按照欧式距离计算，那么A点相对B点就更加接近绿点，但是考虑到样本分布更像是一个样本基本服从f（x）=x的线性分布，按照马氏距离计算，此时A点相对于B点更像是一个离群点。

相对于欧氏距离，马氏距离的计算会更加考虑总体样本的分布，可以更好地排除样本变量之间的相关性的干扰。它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关，由标准化数据和中心化数据（即原始数据与均值之差）计算出的二点之间的马氏距离相同。

3 主要内容

基于马氏距离的改进SMOTE算法Maha-smote算法

马氏距离在本文中的算法流程：

（1）输入少数类元素x，以及少数类集合D;

（2）计算少数类元素与集合D平均值DM的距离xm=x- DM;

（3）求少数类x和集合D的协方差矩阵S以及协方差矩阵的逆矩陣SI：

（4）最后马氏距离公式计算每个元素的马氏距离mahal（x）。

Maha-smote算法流程是在SMOTE算法上的改進：

（1）对于少数类中每一个样本x，计算它的近邻的欧几里得距离，按照从小到大的顺序排序，将前k个近邻合并为k近邻集合;

（2）根据多数类和少数类样本的不平衡比例设置上采样倍率N，对于每一个少数类样本x.从其k近邻集合中随机选择几个样本，近邻样本为x。;

（3）对于每一个选出的近邻xn，计算其马氏距离mahal（xn），以及中心元素的马氏距离mahal（x）;

（4）比较中心元素x与近邻元素xn的马氏距离，如果mahal（x） >mahal（xn），那么代表x相对于xn更加的靠近边界，因而生成的元素则要相对靠近xn，反之则需要靠近x，保证生成的新元素更加的接近集合中心;

（5）因此生成元素的公式则变成：

依据马氏距离生成的元素更加靠近集合中心，生成的新元素质量将会更高，由噪声数据生成的新元素对总体带来的影响将会被减少到更小的程度，从而提高分类算法的整体性能。

4 实验与分析

4.1 不平衡数据集评价指标

在传统的分类学习方法中，常用的方法是采用分类精度（正确分类的样本占总样本的比例）作为判断分类器好坏的指标。但是对于不平衡数据集来说，用分类精度来评价分类器的性能是不合理的。例如当少数类比例非常少时，即使将全部少数类都分为多数类，总精度仍然能达到很高的程度。但这样的分类器是没有实际意义的，其对少数类的分类正确率非常低。

对于不平衡问题，已有新的评价标准，如F-Measure方法。这里F-Measure是一种统计量，F-Measure又称为F-Score，F-Measure是Precision和Recall加权调和平均，常用于评价分类模型的优劣程度。关于F的计算公式为：

其中β是参数，P是精确率（Precision），R是召回率（Recall）。

如表1所示，通常情况下我们可以对识别数据的情况分成四类：

β<1时代表着更加注重精确率（precision）;β>1时则代表着更加注重召回率（recall）的作用。这里参数β取1时，代表着精确率（precision）和召回率（recall）同样重要，那么F-Measure值越高代表着性能越好。因此，它可以作为不平衡数据集分类问题的一种有效评估标准。

ROC曲线AUC面积

ROCc9]曲线的设置横坐标为假正类率（False Positive Rate），设置纵坐标为真正类率（True Positive Rate），相应的还有真负类率（True Negative Rate）和假负类率（False Negative Rate）。这四类指标：

（1）假正类率（FPR）：判定为正例却不是真正例的概率，即真负例中判为正例的概率;

（2）真正类率（TPR）：判定为正例也是真正例的概率，即真正例中判为正例的概率;

（3）真负类率（FNR）：判定为负例却不是真负例的概率，即真正例中判为负例的概率;

（4）假负类率（TNR）：判定为负例也是真负例的概率，即真负例中判为负例的概率。

ROC曲线的特点：

（1）ROC曲线能查出不同的阈值对分类器的泛化性能影响;

（2）ROC曲线越靠近左上角，代表着分类器模型的准确性就越高;

（3）ROC曲线上最靠近左上角的点是分类错误最少的最好阈值;

（4）可以比较不同的分类器的性能。将各个分类器的ROC曲线绘制到同一坐标中，直观地比较优劣。

我们如果进行分类器的比较，若一个分类器的ROC曲线把另一个分类器的曲线完全包住，我们就能轻易地判断两者优劣程度;但是如果两个分类器的ROC曲线发生交叉，那么就很难判断两者的优劣程度。此时我们如果仍要进行判断可以使用AUC[10-11]，就是ROC曲线下方的面积（Area under the Curve），在比较不同的分类模型时，可以将每个模型的ROC曲线都画出来，比较曲线下面积来判断组好的模型是什么。其意义是。

（1）因为是在1x1的方格里求面积，AUC的值必定在0到1之间。

（2）假设一个阈值，阈值以上是正类，以下是负类;若随机抽取一个正类样本和一个负类样本，分类器正确判断正类样本的值高于负类样本的概率= AUC。

（3）总的来说：AUC值越大的分类器，正确率越高。

4.2 实验结果与分析

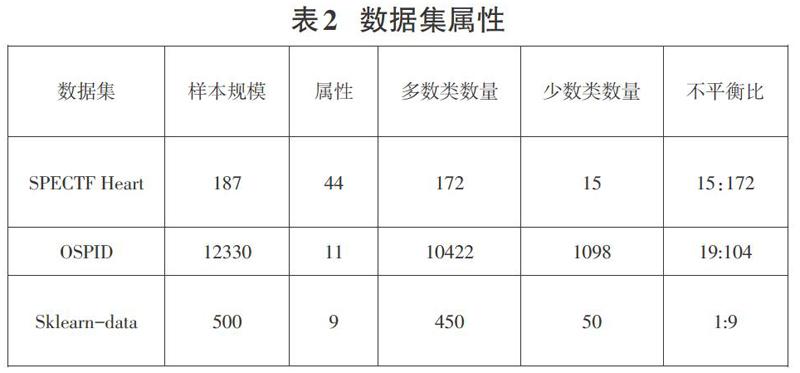
为了评估Maha-smote算法的性能，本次研究使用的数据集是UCI平台的SPECTF Heart、Online Shoppers Purchasing In-tention Dataset以及采用sklearn的相关技术随机制造数据集Skleam-data。下表显示每个数据集的样本规模、属性以及多数类少数类数量和不平衡比。可以看到每个数据集的数据分布非常不平衡，可以很好地使用算法进行研究。

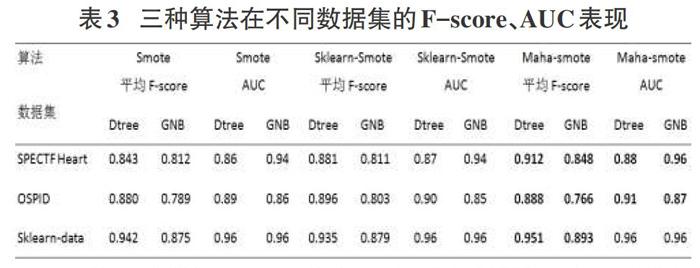
除此之外，本文在生成新数据的时候还使用了SMOTE经典算法以及skleam库里的smote方法进行对比，为了公平起见，k近邻的选择均将k值设置为5，借此展示Maha-smote算法的性能，然后还将使用决策树、Gaussian Navie Bayes来采用K折交叉验证来对经过不同SMOTE算法进行采样后的新数据进行预测，分类的效果将使用F-Measure、AUC这些评价指标进行展示。

在使用决策树和GNB分类器对不同采样算法在三个数据集进行采样后的表现，可以看到相对于经典SMOTE算法和sklearn-smote方法的表现，Maha-smote算法的f-score、AUC评分均高于前两个采样方法，且在某些方面和GNB-起搭配能够对非平衡数据集进行更好的预测。

5 结束语

本文提出將马氏距离结合到smote算法来更好的生成新数据，它可以更好地提高新生成样本的样本质量，可以降低边界元素在生成样本之后对经过采样后造成不好的影响，可以让生成元素更加接近集合中心，提高整个新少数类集合的总体质量，以便于后续的分类算法更好地对数据进行预测等操作。不过Maha-smote对于远离边界的数据或是噪声数据并没有进一步的操作，如果能够进一步地进行噪声数据方面的识别与处理，如果删去或是降低其生成元素时的占比，那么算法可能还将进一步优化，可以提高运行效率。

参考文献：

[1]谢艳晴.基于非平衡数据集的贷款违规预测研究[D].荆州：长江大学，2019.

[2] Provost F，Fawcett T.Robust classification for imprecise envi-ronments[J].Machine Learning，2001，42（3）：203 -23 1.

[3] Chawla N V，Bowyer K W，Hall L O，et aI.SMOTE：synthetic mi-nority over-sampling technique[J].Journal of Artificial Intelli-gence Research，2002，16：321-357.

[4] Torres F R，Carrasco-Ochoa J A，Martinez-Trinidad J F.SMOTE-D a deterministic version of SMOTE[M]//LectureNotes in Computer Science.Cham：Springer Intemational Pub-lishing，2016：177-188.

[5] Han H，Wang W Y，Mao B H.Borderline-SMOTE：a newoversampling method in imbalanced data sets learning[C]//ln-ternational Conference on Advances in Intelligent Computing.Berlin：Springer一Verlag，2005.878—887.

[6]Nghe N T，Janecek P，Haddawy P.A compamtive analysis oftechniques for predicting academic performance[C]//Proc ofthe 37th IEEE Fmntiers in Education Conference—dobal Engi—neering：Knowledge Without Borders，2007：7—12.

[7]徐丽丽，闫德勤.不平衡数据加权集成学习算法[J]，微型机与应用，2015，34（23）：7—10.

[8]李克文，林亚林，杨耀忠.一种改进的基于欧氏距离的SDR—SMOTE算法[J].计算机工程与科学，2019，41（11）：2063—2070.

[9]AUC一—百度百科https：//baike.baidu.com/item/AUC/19282953.

[10]汪云云，陈松灿.基于AUC的分类器评价和设计综述[J].模式识别与人工智能，2011，24（1）：64—71.

[11]Evaluation of clustering.斯坦福大学自然语言处理实验室网站https：//nlp.staJlford.edu/IR-bookmtInl/lltIIlleditioIl/evalua—tion—of-clustering一1.htInl[2013—04—20].

【通联编辑：梁书】

作者简介：徐湘君（1997-），河南固始人，长江大学研究生，研究方向为数据分析;刘波涛（1980-），男，副教授，博士，硕士生导师，王要研究方向：软件开发技术、人工智能技术、物联网应用技术、计算机在石油勘探及开发中的应用研究等。