波浪与高桩承台式结构作用的试验研究*

张慈珩， 郭 泉， 杨会利， 耿宝磊

(1. 交通运输部天津水运工程科学研究院， 港口水工建筑技术国家工程实验室， 天津300456；2. 天津大学， 天津300072； 3. 河海大学， 江苏 南京210098)

嵊泗县位于杭州湾以东、 长江口东南， 北纬30°24′～31°04′、 东经121°30′～123°25′， 是浙江省最东部、 舟山群岛最北部的海岛县， 历来是军事要塞， 又是国际海轮进出长江口的必经之道， 与长江三角洲各地区特别是上海市有着密切的联系，特殊的区位优势是嵊泗县经济和社会发展的重要条件。 而拟建的泗礁岛车客渡码头工程位于嵊泗主岛西北侧， 是区域重要的客运交通枢纽， 其具体位置及周边态势见图1。

图1 工程位置及周边态势

关于高桩承台式结构与波浪的相互作用问题，徐博等[1]基于RANS 模型建立波浪与高桩承台相互作用的三维数值模型， 研究了承台受到的水平及竖向波浪力时程特性、 承台周围流场以及净空对波浪荷载的影响规律； 张忠中[2]则针对福建目前海上风电发展情况及工程海域特点， 结合工程实例， 研究高桩承台在海上风机基础中的应用；而黄津等[3]以工程实例为研究对象， 依据实际结构尺寸建立高桩码头的有限元模型， 探讨波浪力对高桩码头结构的影响； 刘逸敏等[4]则以深海桥梁建设中广泛采用的群桩基础为研究对象， 发展了淹没承台下桩柱波浪作用力的工程计算方法；另外周静姝等[5]、 周子明[6]则研究了承台结构在波浪作用下的水动力特性问题。

本文依据前人的研究成果并依托相关工程实例， 进行一定比尺的物理模型试验， 测量高桩承台结构的堤前后波高、 上水越浪情况及结构受力，分析波浪透射率， 并对堤前挡浪板夹缝处的流速进行测量。 通过分析波浪对不同形式高桩承台结构的作用效果， 进而为该类工程结构设计提供建议与依据。

1 试验条件

1.1 试验水位

试验水位条件为: 50 a 一遇的极端高水位3.01 m， 设计高水位2.06 m， 设计低水位-1.89 m。

1.2 波浪条件

试验波要素参考已有的研究成果[7]， 码头处测点布置见图2[8]， 并选取2#点位置的波浪作为试验波浪条件； 试验主要针对重现期为50 a 一遇的波浪情况， 具体波要素见表1。

图2 计算点布置

表1 试验波要素

1.3 工程结构方案

工程设计方案遵照《防波堤与护岸设计规范》[9]要求， 其中原设计直桩方案平面与断面见图3， 结构形式为常规高桩承台结构， 共布置4排桩。 其中迎浪侧第3 排为消浪排桩结构， 采用φ2 000 mm直桩， 桩间有插入式肋板， 肋板插入底高程至泥面， 肋板间距50 mm； 胸墙高度为1. 5 m， 顶高程为7. 5 m； 后3 排均采用φ2 000 mm直桩。

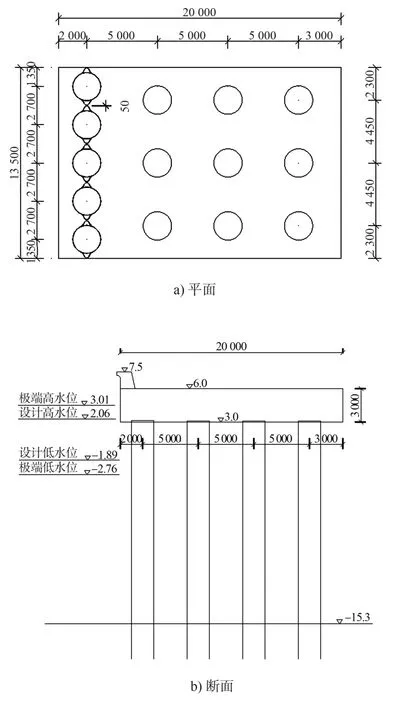
图3 原设计直桩方案(高程: m； 尺寸: mm。 下同)

原设计斜桩(斜度5∶1)方案平面与断面见图4， 其在原设计直桩方案基础上， 将第1 排消浪直桩改为斜度5∶1 的消浪斜桩， 其他因素与原设计直桩方案相同。

图4 原设计斜桩(斜度5：1)方案

修改方案的断面结构形式见图5， 将原设计直桩方案的4 排直桩更改为4 排斜度为6∶1 的斜桩；胸墙高度为1.2 m， 顶高程为5.7 m； 第1 排为消浪桩， 同样在桩间布置了和原方案相同的肋板结构。

图5 修改方案断面

2 试验设备及方法

2.1 相似准则与模型比尺

模型按重力相似准则设计， 结构断面尺寸满足几何相似； 另外根据试验场地、 现有块体质量及试验要求， 选用的模型几何比尺为31.75， 时间比尺为5.63， 力比尺为32 006。

2.2 试验设备

试验在交通运输部天津水运工程科学研究院波浪试验大厅水槽中进行， 水槽长65 m、 宽1 m、高1.3 m。 造波机为电机伺服驱动推板吸收式造波机， 可以产生规则波与不规则波。

另外模型的高程用水准仪控制， 长度用钢尺测量， 水位通过测针进行测量， 波高采用三维浪高仪， 并通过日本三井造船厂开发的多方向波测量系统对波高进行采集分析， 模型波浪力采用SG2008 型微型点压力采集系统对采集到的点压力进行处理， 试验过程中使用摄像机记录波面过程和上水、 越浪等试验现象。

2.3 试验方法

1)波浪模拟。 试验采用频谱不规则波， 频谱考虑《港口与航道水文规范》[10]中规定的波谱， 选用JONSWAP 谱。

2)越浪量测量。 越浪量统计即在测量点用接水装置接取越浪水体， 通过测量质量或体积从而得到模型的越浪量。 不规则波截取一个完整波列的总越浪水体作为相应历时的总越浪量， 然后计算单宽平均越浪量， 并按照相似准则， 将模型越浪量换算成原体越浪量。

3)堤后次生波测量。 为验证掩护效果， 在堤后布置波高传感器测量因透射和越浪产生的堤后次生波， 堤后共布置了10 个波高传感器， 距防波堤后 沿 距 离 分 别 为3.18、 19.05、 34.93、 50.80、66.68、 82.55、 98.43、 114.30、 130.18、 146.05 m，传感器布置见图6。

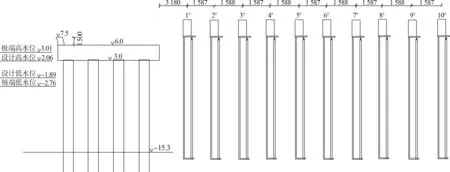
图6 堤后次生波传感器布置

4) 波压力测量。 依据《波浪模型试验规程》[11]和试验要求， 在迎浪侧消浪桩、 挡板、 码头面顶部布置波压力传感器； 各传感器高程见图7。试验在两种水位重现期为50 a 的波浪作用下， 按照迎浪面2.7 m(即一桩与两侧消浪板宽度之和)计算单位宽度的总力。

图7 波压力传感器布置

5) 堤前波生流流速测量。 消浪桩间缝隙较小， 为50 mm， 在波浪作用下消浪桩前后产生较大的水位差， 进而会产生较大的流速， 易造成桩局部冲刷， 故需要对消浪桩间的流速进行测量。流速测量在原设计方案直桩结构中进行， 测量点底高程为-13.71 m(模型上距底5 cm)， 测点正对消浪桩间缝隙， 测点位置见图8。

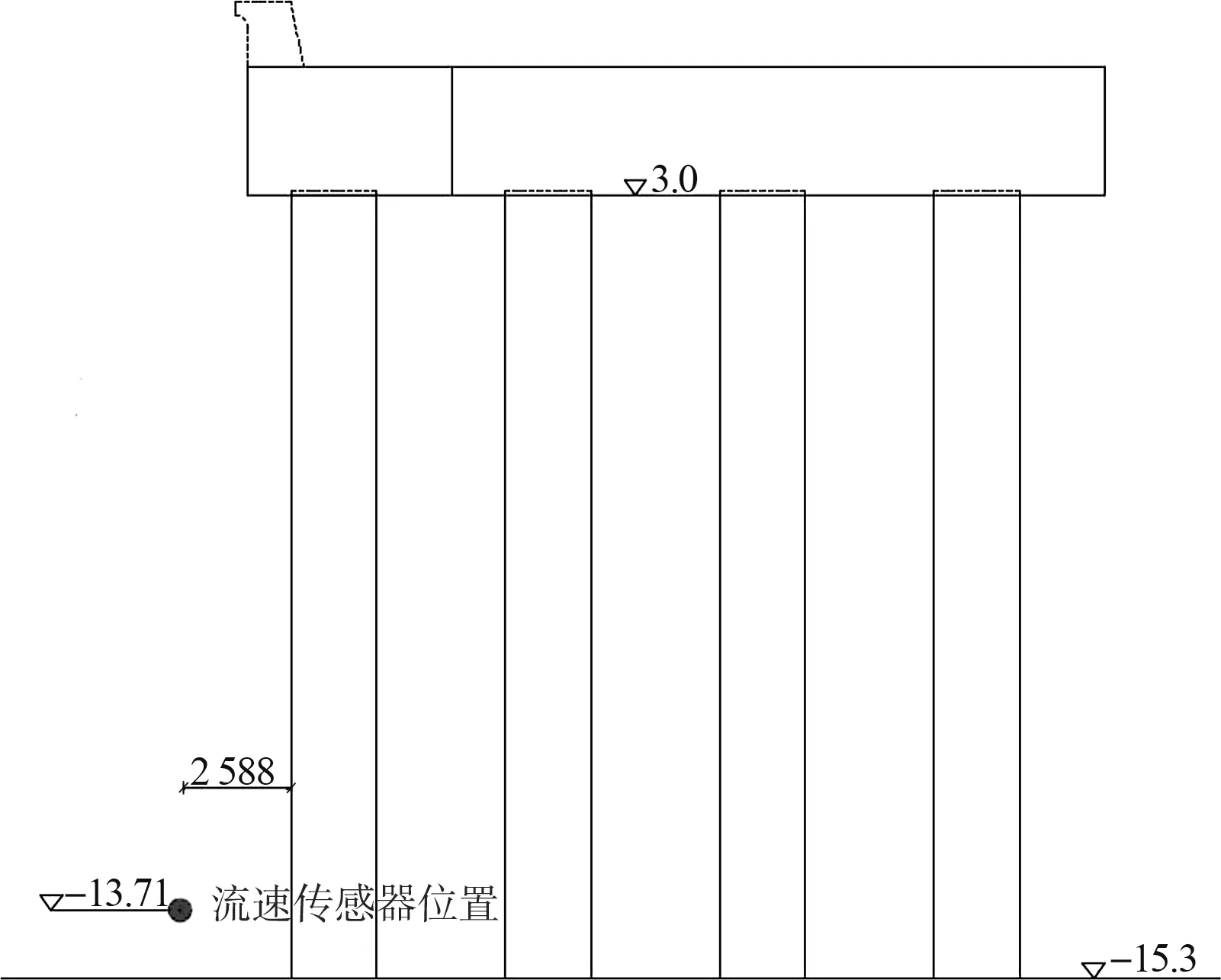
图8 底流速传感器布置

3 试验结果与分析

3.1 堤后次生波

在重现期为50 a 的波浪作用下， 极端高水位作用时堤后次生波波高结果对比见图9a)、 b)，设计高水位作用时堤后次生波波高结果对比见图9c)、 d)； 极端高水位作用时堤后次生波透射率(堤后与堤前波高之比)结果对比见图10a)、 b)，设计高水位作用时堤后次生波透射率结果对比见图10c)、 d)。

图9 堤后次生波波高对比

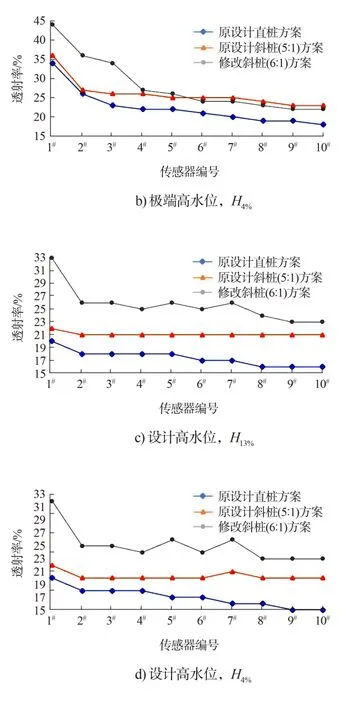
图10 堤后次生波透射率对比

可以看出， 原设计直桩方案在极端高水位重现期为50 a 的波浪条件下， 堤后次生波波高较大，两种不同波浪累计频率下的平均透射率为22.7%，在设计高水位、 重现期为50 a 的波浪条件下， 两种不同波浪累计频率下的平均透射率为17.2%；另外随着与堤距离的增加， 次生波的波高和透射率逐渐衰减， 且在堤后附近位置处衰减较快， 之后衰减速度放缓； 针对整个试验结果而言， 堤后最大波高值可达2.0 m。

原设计斜桩(斜度5∶1)方案在极端高水位、 重现期为50 a 的波浪作用下， 两种不同波浪累计频率下的平均透射率为26.45%， 在设计高水位重现期为50 a 条件下， 两种不同波浪累计频率下的平均透射率为20.7%， 堤后最大波高值可达2.16 m，可见原设计斜桩(斜度5∶1)方案堤后最大波高和平均透射率均大于原设计直桩方案。 此斜桩方案对比原设计的直桩方案， 前排的消浪直桩换成斜桩， 分析可知斜消浪桩与直消浪桩相比， 斜消浪桩的堤后次生波透射率会增大， 并导致堤后的最大波高也增大； 另外斜消浪桩后的波高及其透射率也会随着与堤距离的增加而衰减， 对于直消浪桩和斜消浪桩两种设计方案， 波高的衰减幅值在两种水位和两种波浪累计频率下基本一致， 但直消浪桩后的次生波透射率衰减更快， 且衰减幅值更大， 这种现象在设计高水位时表现得更加明显，分析后认为是设计高水位时堤后次生波受越浪量的影响比极端高水位时小造成的。

修改方案斜桩(斜度6∶1)试验中， 根据透射率结果可知: 在极端高水位、 重现期50 a 的波浪条件下， 两种不同波浪累计频率下的平均透射率为28.6%， 设计高水位、 重现期为50 a 条件下， 两种不同波浪累计频率下的平均透射率为25.0%；综合整个试验结果， 堤后最大波高可达2.63 m；随着与堤距离的增加， 次生波波高与透射率也逐渐衰减， 与原方案相同； 该方案与原方案中的两种形式相比， 其胸墙顶高程降低， 平均透射率增加， 堤后最大波高也显著增大； 堤后次生波和透射率都比原设计的两种方案要大， 且衰减速度和衰减幅值也更大， 在极端高水位作用时此现象更加明显； 在5#传感器(图6)之后的水域， 该修改方案的波高以及透射率结果已经小于原设计斜桩(斜率5∶1)方案的结果， 分析主要是修改方案的顶高程较低， 在极端高水位作用时堤顶越浪量远大于原设计直桩和斜桩方案的越浪量， 造成1#传感器位置处(图6)修改方案的波高和透射率结果比原设计方案的波高和透射率结果大得多； 而修改方案的透射衰减速度更快， 这是因为通过越浪在堤后产生的次生波的衰减速度要大于透过消浪桩间缝隙的波浪在堤后产生的次生波所导致。

3.2 越浪情况

极端高水位和设计高水位(重现期均为50 a)的波浪作用下， 各方案越浪量及越浪冲击最远距离(距胸墙前沿)结果见表2(越浪率为一个波列中越浪波数量与波列中波总数量的百分比)。

表2 越浪情况结果

根据试验结果可知， 原设计直桩方案在极端高水位和设计高水位(重现期均为50 a)波浪作用下， 越浪量分别为252.6 和18.3 L∕(m·s)， 越浪冲击范围分别为7.0 和3.2 m； 原设计斜桩(斜度5∶1)方案在极端高水位和设计高水位(重现期均为50 a)波浪作用下， 越浪量分别为178.6 和13.2 L∕(m·s)，越浪冲击范围分别为7.6 和3.8 m； 与原直桩方案相比可知将直桩换为斜桩时， 越浪量显著降低， 结合两原设计方案堤后次生波波高和透射率结果分析可知， 堤前波浪更易透过原设计方案的斜桩消浪桩， 即在波浪沿斜面爬升的过程中有更多的水体透过消浪桩的缝隙进入堤后， 从而使越过堤顶进入堤后的水体减少， 造成所测得的越浪量减小；另外修改斜桩(斜度6∶1)方案试验在两种水位(重现期均为50 a)的条件下， 越浪量分别为486.6 和131.1 L∕(m·s)； 越浪冲击范围分别为11.1 和6.4 m。 且在极端高水位(50 a 重现期)下， 越浪率高达63%； 该修改方案与原设计方案的两种形式相比， 由于胸墙顶高程较低， 导致越浪量远大于两种原设计方案的越浪量， 且越浪冲击范围也更大， 此形式下的结构更应注意顶面的排水问题。

3.3 波浪力

3.3.1 原设计直桩方案

统计各传感器数据， 各处测点的最大压强均出现在极端高水位， 结构顶板表面最大压强出现在6#波压力传感器， 可达113.43 kPa， 分析其主要是由于越浪水体冲击造成的； 而结构迎浪面最大压强出现在15#波压力传感器， 可达91.32 kPa； 水平力最大值出现在极端高水位， 可达4 255.22 kN∕2.7 m，见图7a)。

3.3.2 修改斜桩(斜度6∶1)方案试验

统计各传感器数据， 由试验结果可知各测点最大压强均出现在极端高水位， 此时结构顶板表面最大压强出现在5#波压力传感器， 可达58.48 kPa；结构迎浪面最大压强出现在14#波压力传感器， 可达85.87 kPa； 水平力最大值出现在极端高水位，可达3 975.28 kN∕2.7 m， 见图7b)。

该修改方案与原直桩方案相比， 所受的水平力最大值减小， 各处所受最大压力也相应减小。

3.4 堤前流速

针对原直桩方案测量堤前流速， 不同水位条件下， 消浪桩前波生流流速结果见表3。 可以看出， 在极端高水位(重现期为50 a)的波浪条件下，最大流速可达6.64 m∕s； 设计高水位(重现期为50 a)的波浪条件下最大瞬时流速为5.79 m∕s。 由于流速较大， 易造成桩局部冲刷， 故在工程设计中对于此类消浪桩结构， 应考虑对消浪桩内外采取一定的防护措施。

表3 消浪桩前波生流流速结果

4 结论

1)在同等条件下， 消浪直桩后的堤后次生波的波高和透射率都小于消浪斜桩， 故消浪直桩方案对于桩后水域而言具备更好的泊稳条件； 但由于消浪斜桩有斜面存在， 波浪在斜面爬升的过程中能量会被损耗， 从而在入射波和反射波叠加后， 消浪斜桩前的波高会小于消浪直桩前的波高， 此时对于桩前水域， 消浪斜桩拥有更好的泊稳条件。

2)本工程设计方案采用消浪桩结构， 消浪桩间距较小， 仅为50 mm； 根据直桩试验中观测到的流速结果可知， 桩间缝隙处流速较大， 容易造成该处局部冲刷， 故对于该类消浪桩， 应采用适宜的方式对消浪桩内外做一定的防护。

3)本工程修改方案的挡浪墙顶高程仅为5.7 m， 根据试验观测结果可知， 其越浪量及对码头上部结构的冲击均较大， 同时还会引起堤后次生波的增大， 堤后兼作码头时， 不利于船舶的泊稳； 另外在极端高水位情况下， 越浪冲击距离也较大， 故应注意结构上部设施的安全以及排水问题。

4)本工程所采用的消浪结构， 所受波浪冲击较大， 由于物理模型缩尺效应的影响， 其破波作用由于夹气量的不同， 模型破波冲击会弱于原型，而时间比尺又会造成模型的受力时间长于原型从而使结构响应偏于保守， 故在相关设计时应注意受力冲击的取值问题。

5)本工程位于岛屿群内， 海域地形条件复杂，受地形折射和岛屿掩护影响， 波浪传播也十分复杂； 而受二维断面物理模型限制， 模型中无法反映波浪方向、 周边地形结构等因素的影响； 因此建议后续研究可采用整体波浪物理模型， 对波浪分布、 波浪对结构物的作用做进一步的模拟研究。