求图形面积的方法
2020-11-27 02:37
小学生学习指导(高年级) 2020年11期
计算一些组合图形的面积,除了需要常用的面积计算公式外,还可以通过转化、添加辅助线等方法加以解答。
1.合并求和法。有些组合图形面积是要把它分成几个常见的基本图形,然后求出各基本图形的面积,最后再把这几个基本图形的面积合起来。例如,计算图1的面积。(单位:厘米)

图1

图2
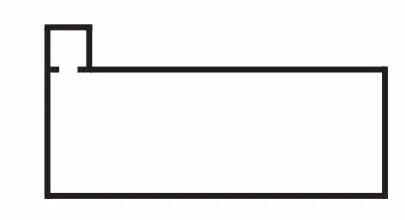
图3
图1是一个不规则图形,无法直接求出,我们可以添加辅助线,把它分成两个长方形,如图2,先分别求面积然后相加:4×1+(8-1)×3=25(平方厘米);也可以分成一个长方形和一个正方形,如图3,(4-3)×1+8×3=25(平方厘米)。
2.去空求差法。所谓去空求差法,就是从大面积里去掉空白部分的面积。例如,求下图阴影部分的面积。(单位:厘米)

要求阴影部分的面积就是从两个正方形里去掉空白三角形的面积。7×7+4×4-(7+4)×7÷2=65-38.5=26.5(平方厘米)。
3.割补平移法。就是把图形通过割补、平移转化成规则的图形,从而化难为易,化繁为简。例如,计算图4中阴影部分的面积。(单位:厘米)

图4

图5
要求阴影部分的面积,可以先把左面阴影部分向右平移,与右边阴影部分合在一起,然后再把左边的三角形剪下来,补到右边,转化成一个长方形,如图5。(10-2)×8=64(平方厘米)。
4.等积代换法。就是把要求部分的面积转化成等量图形的面积。例如,下图是两个完全一样的梯形,求阴影部分的面积。(单位:厘米)

上图阴影部分是一个不规则的六边形,不能直接求出面积。比较发现,两个完全一样的梯形,同时去掉重叠部分,余下部分的面积相等,即阴影部分的面积和下面的梯形面积相等。(10-2+10)×2÷2=18(平方厘米)。
猜你喜欢
理科爱好者(教育教学版)(2022年1期)2022-04-14
文苑(2020年11期)2020-11-19
中国诗歌(2019年6期)2019-11-15
数学大王·低年级(2019年4期)2019-05-13
初中生世界·九年级(2017年9期)2017-10-13
数学大王·中高年级(2016年4期)2016-05-14
中学生数理化·八年级数学人教版(2016年2期)2016-04-13
小学生时代·大嘴英语(2014年1期)2014-02-28
中学生英语·中考指导版(2008年5期)2008-12-19
中学生数理化·八年级数学北师大版(2008年9期)2008-10-15
- 小学生学习指导(高年级)的其它文章
- 筛选条件 巧妙解题
- 有关圆的知识
- 海宝小队护城记之交锋失败
- 求草坪的面积
- 剪一剪,折一折 纸模汽车
- 列方程解应用题

