一种适合低压大电流输出的多路交错LLC谐振变换电路

包尔恒

（广东水利电力职业技术学院，广东 广州 510925）

0 引 言

LLC谐振变换器作为DC/DC变换拓扑，与其他如移相全桥、双管正激、全桥和半桥硬开关相比，在合理的设计条件下具有以下优势和特点。第一，可以得到较宽的输出电压范围，且几乎全负载范围实现ZVS。在开关频率低于谐振频率时，开关管关断电流为励磁电流，可以通过励磁电感量进行控制。此外，副边整流二极管电流自然过零，几乎没有反向恢复。这些特点有利于优化效率。第二，额定输出状态可以设计在谐振频率处，而正弦电流波形使开关频率的高次谐波分量很小，且工作频率低于谐振频率时，副边整流二极管几乎没有反向恢复，大大减轻了由此造成的辐射问题，有利于EMI的设计。第三，副边不用体积较大的差模电感进行滤波，节省了体积和成本。

在低压大电流输出电源装置中，采用单一的LLC谐振变换电路，存在输出端电流脉动过大的问题，需要过多的电容来滤除输出电流脉动。过多电容的电路基本上仅是理论可行，一是需要的空间和体积大，成本高；二是因工程上布局布线的空间限制而存在可靠性瓶颈，会造成最靠近副边整流管（二极管或同步整流MOSFET）的电解电容过热，使得可靠性存在很大隐患。

针对上述问题，本文提出一种采用LLC谐振DC-DC变换，通过多路交错（本文以星型连接方式的原边LLC电路六路高频交错，副边为12路交错的电路结构，输出20 V/1 000 A为例）的电路拓扑结构，可有效解决上述问题，具有高效、高功率密度、低成本以及高可靠性等优势。

1 电路结构及控制策略

LLC谐振变换器有半桥结构、全桥结构以及三电平结构等，基本工作原理类似。以半桥LLC谐振变换器为例，电路结构如图1所示，频率-增益特性如图2所示（直流增益G*dc=2nM=2nUo/Ui）。

图1 单相半桥LLC主电路

频率-增益特性表达式为[1]：

图2 LLC谐振变换器频率-增益特性

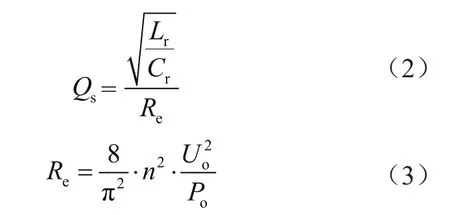
式中，Uo为输出电压，Ui为输入电压，Qs为品质因数，Re为副边折算到原边的负载阻抗，n为原副边匝比，Po为输出功率。

对于交错并联LLC谐振变换器，现有很多相关文献研究[2-3]。三相星型谐振变换器如图3所示。

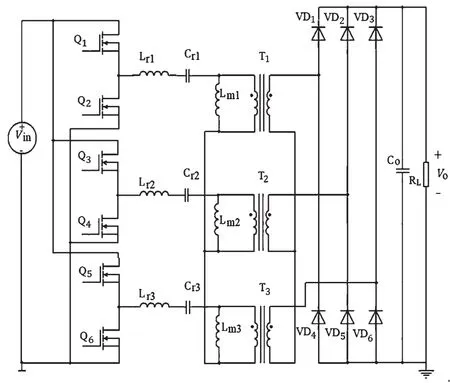
图3 三相星型交错LLC谐振变换电路

三相星型交错并联LLC谐振变换的等效电路，如图4所示[3]。

根据三相星型联结电路原理，有：

图4 星型交错并联LLC谐振变换器等效电路

其中，Zk、Zrk及Zmk（k=1、2、3）的计算表达式如下：

它的分析方法和三相星型联结电路原理类似[4]，每一相变换等效电路如图5所示。

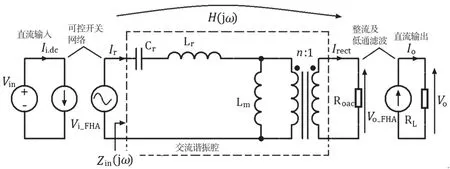
图5 谐振变换器等效电路图

谐振腔输入电压和变压器副边电压为阶梯方波，图6中变压器原副边匝比为10:1，幅值分别是输入电压Vin和输出电压Vo的2/3，台阶电压为其峰值的一半。

Vi_FHA和Vo_FHA分别是谐振输入电压和变压器副边输出电压的基波幅值，开关周期为T，按奇函数计算其基波幅值：

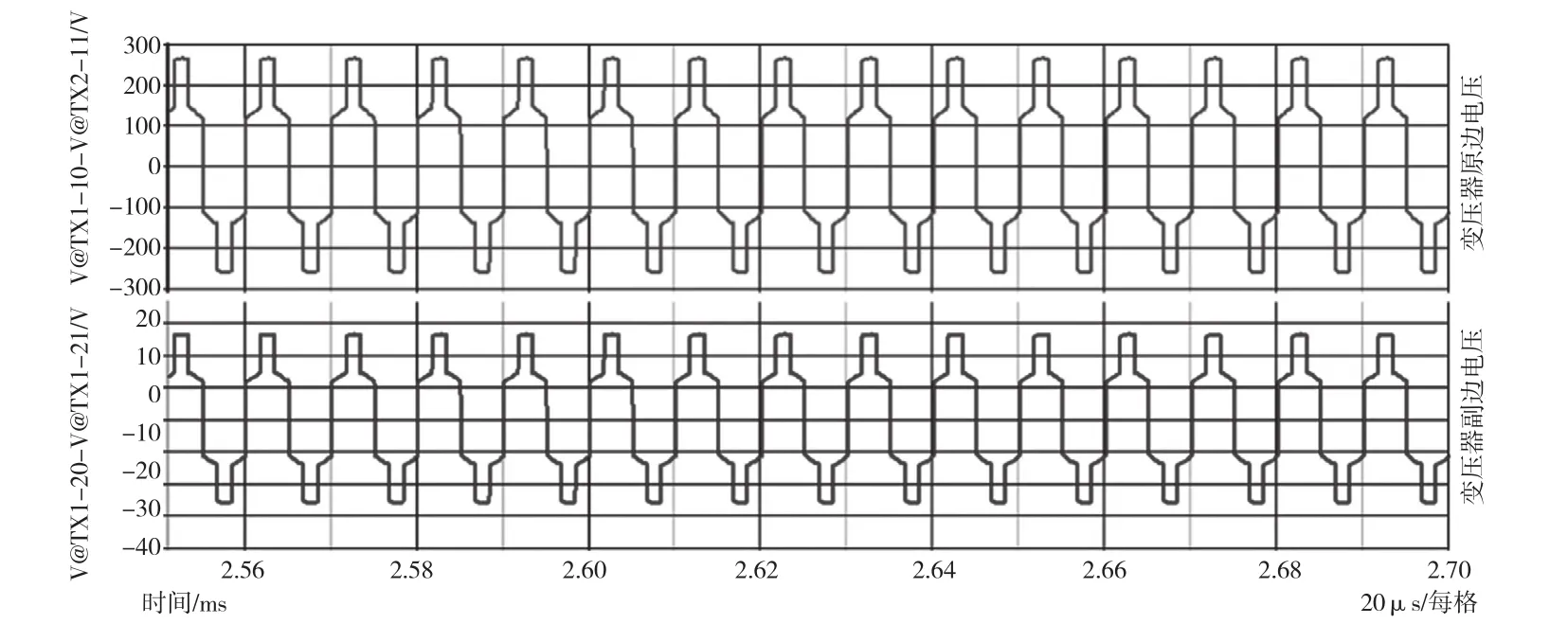
图6 变压器原副边电压波形

所以，谐振腔的增益与输入和输出电压的关系为：

设变压器副边电流峰值为Irect，它与输出负载的关系为：

变压器副边等效负载电阻为：

根据变压器原副边功率关系，计算原边等效电阻为：

从而可得增益M如式（1）所示（不同之处是这里分子为1）。原边谐振电流有效值为：

图7为提出的多路交错并联LLC谐振变换电路结构。原边采用LLC谐振变换电路，共6桥臂，即六路交错，其中分成两个星型连接（为了磁性器件的进一步小型化和离散化，也可以采用变压器原边串、副边并的方式），副边采用全波整流方式，从而输出整流为12路交错。这种多路交错输出，显著降低了输出电流脉动。若效率要求不高，可以选用肖特基二极管整流。更高效率要求时，则可采用MOSFET同步整流。图7主要是为了验证电路方案对输出电流脉动的显著改善，因此采用了二极管整流方式。

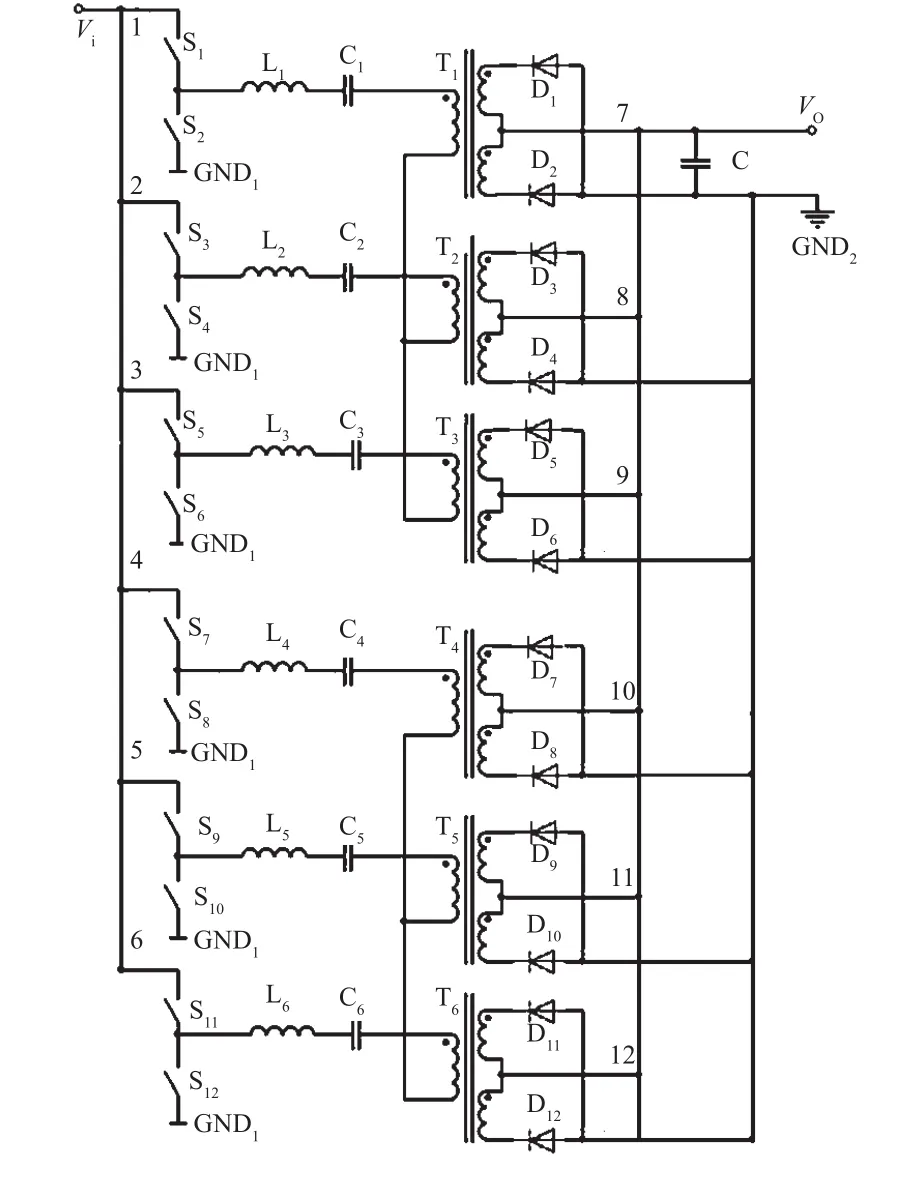
图7 多路交错并联的LLC谐振变换电路结构

电路各开关的驱动控制时序如下：（1）每一个星型连接的3桥臂，其驱动信号相位相差120°；（2）两个不同的星型连接，其驱动信号相位相差30°；（3）每一桥臂上下管驱动信号互补。

2 仿真研究

2.1 单路LLC谐振变换器输出电流纹波

下面以如图8所示的单路全桥LLC谐振变换器的输出电流纹波为例进行仿真分析。电路参数：输入400 V DC，输出20 V DC/1 000 A。仿真模型参数：Lr=22 μH，Lm=180 μH，Cr=117 nF，n=20（变压器原副边变比20:1:1）。输出电压电流仿真效果如图9所示。

图8 单路全桥LLC谐振变换器

图9 输出电流电压仿真效果图

从图9可以看出，输出脉动电流变化幅值约1 500 A，脉动电流很大，需要的输出滤波电容容量和数量甚多，从体积、成本和可靠性考虑均不合适。

2.2 多路交错并联LLC输出电流纹波

以单极性输入电压为例（输入电压也可以为正负电压的方式，如目前三相交流输入时直流母线常见的±400 V的方式，电路各开关的驱动控制时序不变），输入为+400 V DC时，原边6个桥臂都接在400 V DC和地电位之间，6个桥臂上、下管驱动互补，构成星型连接的3个桥臂驱动依次相差120°相位。对图7多路交错并联的LLC电路进行仿真，仿真模型参数设置如下：Lr=22 μH，Lm=180 μH，Cr=117 nF，n=10:1（变压器原副边变比10:1:1）。

输入为400 V DC、输出20 V DC/1 000 A条件下，图10为输出电流脉动仿真效果局部显示图。

图10 输出电流脉动仿真局部图

从图10可以看出：输出脉动电流变化幅值不到40 A，脉动电流很小，大大减小了需要的输出滤波电容容量和数量，使得体积和成本显著减少，基本不存在因布局布线空间过大引入的可靠性隐患。

基于上述电路拓扑结构，选择较低损耗的变压器磁芯、原边MOSFET和同步整流MOSFET，理论估算转换效率可以达到99%及以上，同时解决了目前输出低压大电流电源的技术瓶颈。该电路在控制上需采用数字控制技术，并采用合适的数字信号处理芯片，可实现灵活控制，具有高效、高功率密度以及低成本等优势，并有利于实现批量产品化。

3 结 论

在低压大电流输出电源装置中，传统的移相全桥电路和单一LLC谐振变换器各有其难以克服的缺陷。采用提出的多路交错LLC谐振变换电路，可以大大降低输出电流脉动，减小输出滤波电容的容量和数量，提高电路的可靠性和功率密度，从而解决将LLC谐振变换电路应用于低压大电流输出时的技术瓶颈，大大提高变换效率、功率密度和可靠性。