一种双参数雷达恒虚警率检测算法
杨安东,刘艳苹,林 鹏
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225101)
0 引 言
现代雷达信号检测系统中,为了保证一定的发现概率,一般采取平均选大恒虚警率(CFAR)算法处理[1]。恒虚警率检测算法是一种比较成熟的雷达检测算法,能够连续监测噪声和杂波平均电平的变化,及时调整检测门限电平,使其始终保持在最佳检测门限电平上,保持虚警率概率恒定。同时此种算法对杂波边缘的虚警率有较好的抑制效果,但是在干扰环境、杂波环境以及多目标环境中,检测门限会大幅提高,使得检测性能下降。
本文在平均选大恒虚警检测算法的基础上进行改进,提出一种双参数恒虚警检测算法,可以有效提高在干扰环境、杂波环境以及多目标环境中的检测性能,使其检测概率与噪声环境中的检测概率基本相当。通过仿真分析,比较2种检测算法的检测性能,验证了这种算法的可行性。
1 算法实现
雷达接收机输入信号由雷达回波信号s(t)和杂波噪声n(t)组成,噪声均差为ψ。假设输入噪声空间不相关,且与信号不相关。带通中频滤波器的输出为信号v(t),可写成[2]:
v(t)=vI(t)cosω0t+vQ(t)sinω0t=
r(t)cos(ω0t-φ(t))
(1)
式中:ω0=2πf0,为雷达工作频率;r(t)为v(t)的包络,相位为φ(t)=atan(vQ/vI),下标I,Q分别表示2路正交分量。
当r(t)超过门限值Vt时,系统就检测到一个目标,决策假设可以写为[3]:
(2)
虚警概率Pfa定义为在雷达接收信号中只有噪声出现时信号r(t)的一个样本超过门限电压Vt的概率:
(3)
其中:
(4)
由式(4)可知,Vt的大小由噪声均方差ψ及Pfa决定。
1.1 平均选大恒虚警算法处理
假设D为检测单元,恒虚警处理算法中的噪声均值采用两侧单元平均选大恒虚警的设计方式[4]。框图如图1所示。
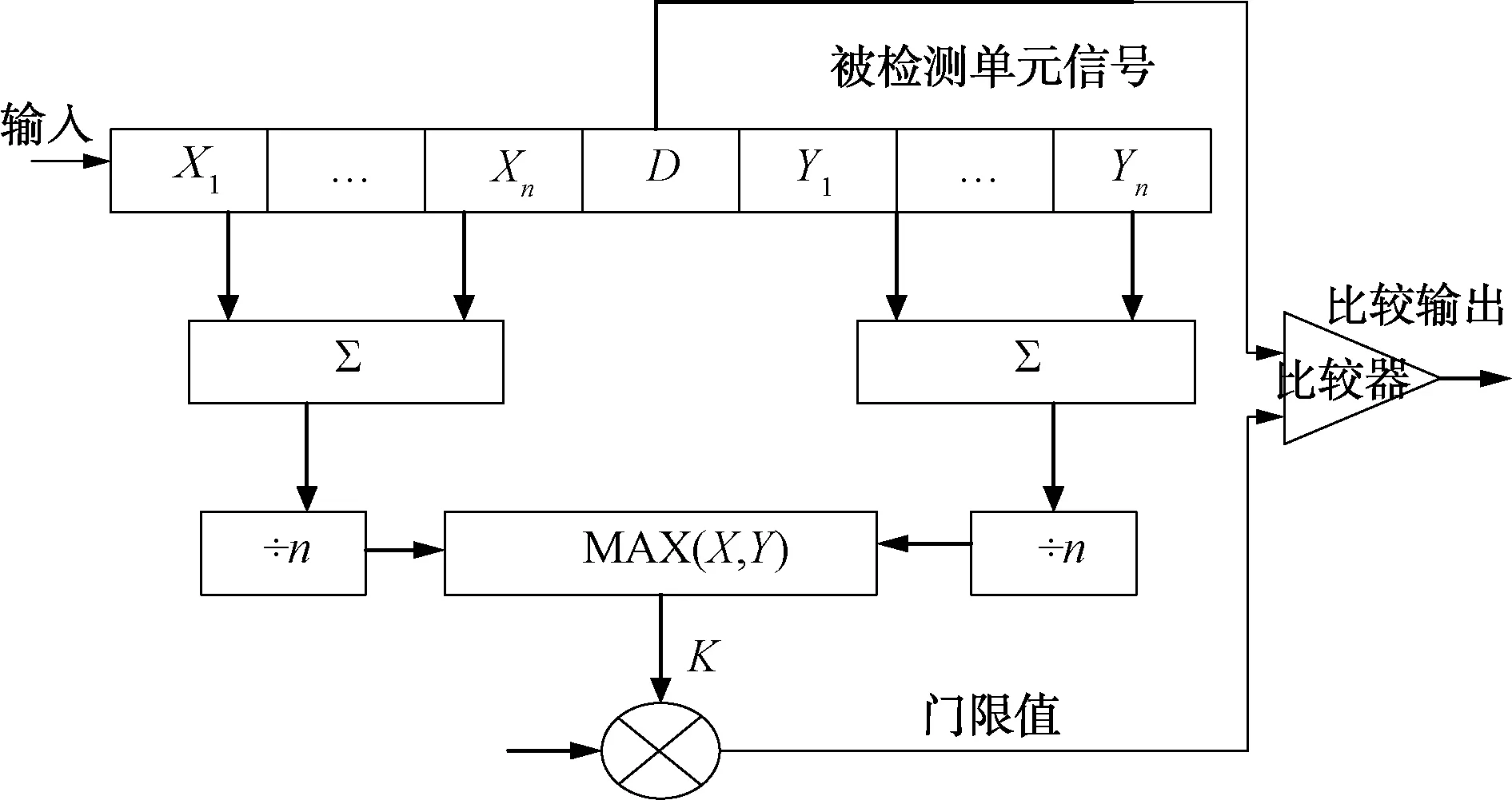
图1 恒虚警算法设计框图
在被检测单元两侧各选n个单元,分别求这n个单元的均值,两者选大后输出,乘以门限系数K作为自适应门限值Vt。为了避免检测单元D本身对门限Vt的影响,统计样本剔除被检测单元,再经过多通道距离单元恒虚警检测及多通道选大输出。
实际应用中,当处于干扰环境、杂波环境以及多目标环境中时,检测单元采样信号会大幅提高,使得检测门限提高,导致检测概率的下降。
1.2 双参数恒虚警算法处理
以平均选大恒虚警检测算法为基础(如图2所示),检测单元两侧各留1个距离单元作为保护单元,各取n+2个距离单元作为参考单元,分别从n+2个参考单元中删除2个最大的干扰,各保留n个单元,共2n个参考单元作为估计杂波均值的样本。
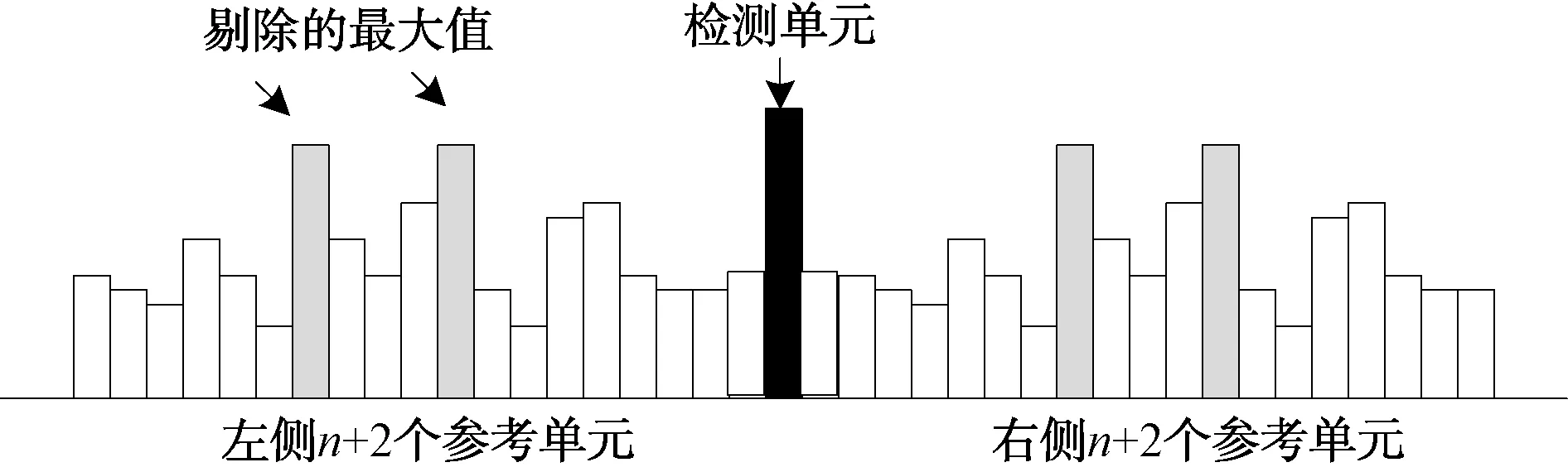
图2 参考单元示意图
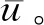
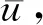

图3 双参数恒虚警算法设计框图
2 仿真分析
考虑一个16通道单元恒虚警检测系统,采集经过动目标检测(MTD)处理后的本地噪声数据和-40 dBm干扰数据,干扰信号分布在滤波器通道8~11。
图4为本地噪声经过MTD处理后的通道8~11的结果,①代表改进后的双参数恒虚警检测门限,②代表恒虚警处理检测门限,③代表经过MTD处理的噪声。由图4可以看出,2种检测方法的检测门限基本相当。

图4 本地噪声恒虚警检测门限对比图
图5为-40 dBm干扰信号经过MTD处理后的通道8~11的结果,①代表恒虚警处理检测门限,②代表改进后的双参数恒虚警检测门限,③代表经过MTD处理的噪声,由图5可以看出,恒虚警处理的检测门限远远高于双参数恒虚警检测门限,其影响就是信号检测性能下降,而双参数恒虚警检测门限较低,可大幅度提高信号检测能力。
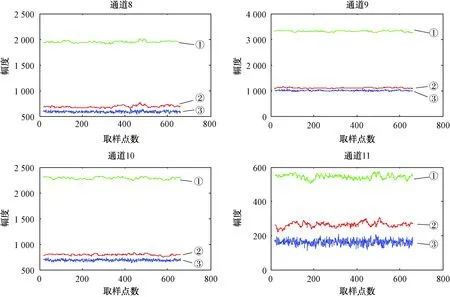
图5 -40 dBm干扰信号恒虚警检测门限对比图
3 结束语
仿真结果证明,双参数恒虚警检测算法可以大幅度提高雷达在干扰环境、杂波环境以及多目标环境中的检测性能。在实际应用中,双参数恒虚警检测模块由剔除最大值模块、串行累加模块、方差估计模块及目标判决等模块组成。该模块可以充分利用现场可编程门阵列的并行处理优势,采用流水线处理方式,实时计算均值和方差,获得恒虚警检测门限,进而实现恒虚警检测功能,具有一定的应用前景。

