2K-H 型行星齿轮装置设计

张 展，武文辉

1上海电力环保设备总厂有限公司 上海 200072

2上海市机械工程学会 上海 200240

3中信重工机械股份有限公司 河南洛阳 471039

目前市场上见到的由锥齿轮组成的行星传动大多是由外直齿锥齿轮组成，如汽车、工程机械上用的行星差速器，有 2 个自由度，用于运动的合成和分解。行星传动的基本构件为太阳轮、内齿圈(或齿轮)和行星架(或转臂、系杆)，若将其中某一构件加以固定，就成为 1 个自由度的行星齿轮传动，常用的行星齿轮传动以 2K-H 型居多[1]。

随着科学技术的发展，加工手段不断完善，CNC机床更新换代及配套 NC 模块日益丰富，直齿或曲线齿的内齿锥齿轮也逐一研制出来，相关设计制造技术日趋完善[2-8]，于是便出现了由内齿锥齿轮啮合的 2K-H 型行星齿轮传动。笔者对由锥齿轮组成的2K-H 型行星齿轮装置进行了简述，给出了几种基本类别的传动比计算公式，并列举总传动比达 100 000以上的组合式锥齿轮行星传动实例，进行了系统啮合损耗和效率的评估。

1 2K-H 型行星传动基本类别

1.1 按啮合方式分类

行星齿轮传动如图1 所示。按行星轮系的基本构件组成来划分，最常用的行星齿轮传动型式为 2K-H型。GB/T 11366 标准规定 2K-H 型行星传动机构定义为：由 2 个中心轮和 1 个行星架组成的行星齿轮传动。2K-H 型行星齿轮传动应用范围广阔，商用产品遍及各行各业。对于 2K-H 型行星齿轮传动，还可按齿轮副啮合方式的不同，细分成几种基本类别。

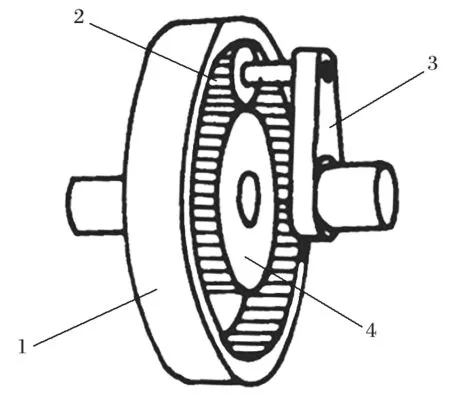
图1 行星齿轮传动Fig.1 Planetary gear transmission device

锥齿轮行星传动，笔者以字母 Z 来表示锥齿轮传动(其他仍采用惯用表示法：N 为内啮合，G 为共用行星轮，W 为外啮合)，于是可以得到以啮合方式特征符号标识命名的传动类别。由锥齿轮组成的 2K-H型行星传动有：ZNGW、ZNW、ZWW、ZNN 型，如图2 所示；由圆柱齿轮组成的 2K-H 型行星传动有NGW、NW、WW、NN 型，如图3 所示。

图2 由锥齿轮组成的 2K-H 型行星传动Fig.2 2K-H planetary gear transmission composed of bevel gears

1.2 主要特点

锥齿轮 2K-H 型行星传动的主要特点是：行星架H可与主轴线(即进、出轴的轴线)呈任意轴交角Σ输出，可应用于多种使用场合，满足各种使用需求。

ZNGW 型、ZNW 型适合广阔功率范围，功率区间基本不受限。ZNGW 型结构简洁，传动效率更高，实用功率范围更大；ZNW 型则具有更大的传动比区间，但其结构相对 ZNGW 型稍复杂些，制造难度亦较高。

图3 由圆柱齿轮组成的 2K-H 型行星传动Fig.3 2K-H planetary gear transmission composed of cylindrical gears

ZWW 型、ZNN 型适合很广阔的传动比范围，但随传动比的增大，齿轮啮合(无功)功率流变大，啮合损耗显著增加，机械传动效率明显下降。巨大的传动比不适合用于功率型动力传递场合，宜用作超大传动比的运动传递。ZNN 型的传动比范围更广，最大可达到 10 000 左右，其对应效率很低，总啮合效率在0.5% 以下。

2 2K-H 型行星传动传动比计算

由图2 可知，当锥齿轮副轴交角Σ=0 时，就可演变成普通的圆柱齿轮传动的 2K-H 型行星齿轮传动，如图3 所示。因此，锥齿轮传动比的计算与普通圆柱齿轮传动的 2K-H 型行星齿轮传动相仿，则图2所示的由锥齿轮组成的 2K-H 型行星传动的传动比可由图3 所示机构的传动比[9]引申得到。

图2、3 中(a)、(b)、(c)3 种类型同标记构件的传动关系完全相同，传动比的计算表达式完全一致。图2(d)、3(d)所示主从动a、b关系是倒置的，传动比互为倒数。

由锥齿轮组成 2K-H 型行星传动的传动比计算公式如下：

(1)ZNGW 型传动比

(2)ZNW 型传动比

(3)ZWW 型传动比

(4)ZNN 型的传动比

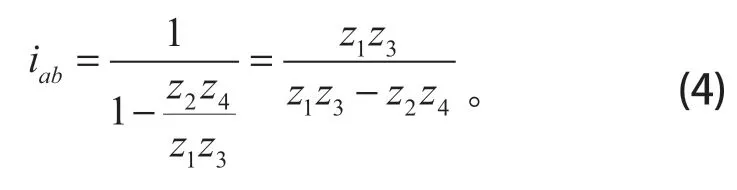
3 行星齿轮传动设计实例

传动比为 262 500 行星齿轮传动如图4 所示。

图4 传动比为 262 500 行星齿轮传动Fig.4 Planetary gear transmission with transmission ratio 262 500

3.1 传动比

图4 所示机构可以看成由z1、z2、z3、z4、H组成的 2K-H(ZWW)型和由z3、z4、z5、z6、H组成的2K-H(ZNN)型复合构成的组合轮系。

由a输入、b输出的传动比

由z1、z2、z3、z4、H组成的行星轮系，转化机构中H相对固定，输出z4、输入a上z1齿轮转向相反，所以其传动比

因此，可得输入端a到行星架H的传动比

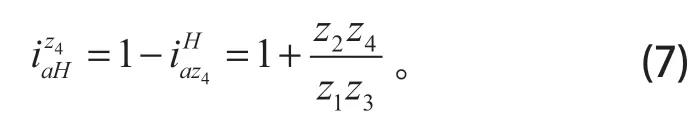
由z3、z4、z5、z6、H组成的行星轮系，其转化机构中z6和z4转向相同，所以其传动比

因此，

由此可得行星架H到输出端b的传动比

将式(7)、(10)代入式(5)，即得到图4 传动装置的传动比

将z1=12、z2=40、z3=40、z4=303、z5=33、z6=250 代入式(7)、(10)，即可求得组合机构各分部的传动比

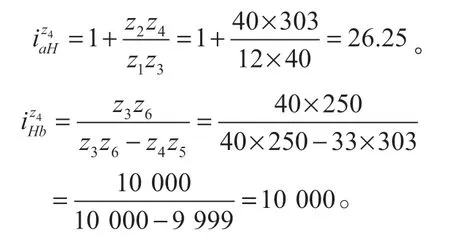
将以上结果代入式(5)，或将已知齿数直接代入式(11)即可得总传动比

iab为正值，说明输出与输入同向旋转。

3.2 传动机构啮合效率估算

若不计节轴处的机械损耗，输入a、输出b转矩分别为Ta=T1、Tb=T6。

3.2.1 静态平衡

(1)不考虑机械损耗，由输入转矩与总传动比求得名义输出转矩

(2)由输入转矩与第一级齿数比求得z2齿轮转矩

(3)从输出端推算z5齿轮转矩

(4)z3沿固定的z4被迫转动，为被动轮，它所受转矩为T5、T2之和

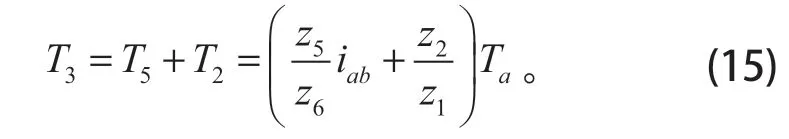
(5)固定齿轮z4所受力矩

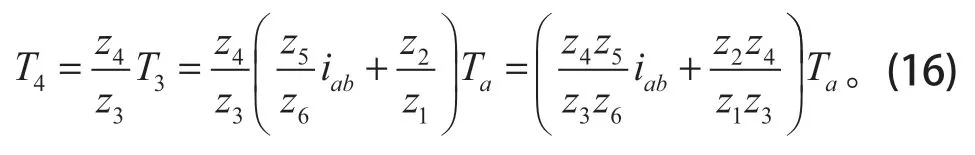
将式(16)变形，结合式(11)、(12)可得

平衡条件：输出、输入实际转向相同，对传动装置支座的作用转矩为输出、输入转矩之差。齿轮z4固定，图4 的转矩平衡条件可描述为T4=Tb-Ta。

由式(17)可知，在不考虑机械损耗时，齿轮所受的阻力矩等于输出转矩与输入转矩之差，系统外力矩处于平衡状态。

3.2.2 啮合功率损耗

采用超大传动比时，总啮合效率值η zΣ很小，Tb＜＜Tb0，Tb不能用输入转矩Ta与总传动比的乘积简单计算，需要建立方程求解。

不计具体损失值，功率以转矩与转速的乘积替代。

(1)齿轮的啮合功率

啮合功率是转化(定轴)轮系中转矩与转速的乘积。转化轮系中齿轮的转速为齿轮绝对转速与行星架转速之差。齿轮z1、z2的啮合功率

(2)啮合损耗及系统啮合效率

①齿轮z1、z2损耗

②齿轮z5、z6损耗

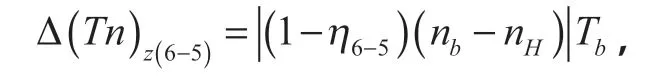
由于

所以

③齿轮z3、z4损耗

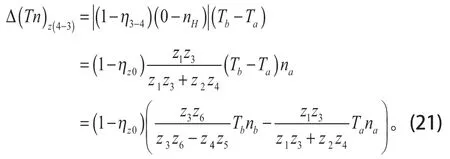
④啮合总损耗及系统啮合效率

齿轮z1～z6总啮合损耗 Δ(Tn)z(1-6)为式(19)、(20)、(21)之和。

输出功率方程

整理上式，得输出功率

式(23)中Tana前面的乘项，即是系统的啮合效率

将各相关齿数代入上式，可得

取ηz0=0.98，则

系统的啮合传动效率约为 0.002 4，输出功率约为输入功率的 0.24%，即额定输出转矩约能达到理想值的 1/500。

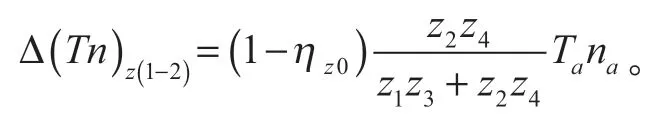
式(21)变为

式(22)变为

式(23)变为

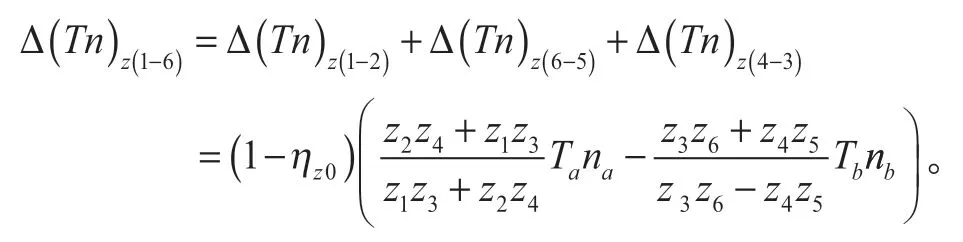
从而可推导出啮合效率估算通式为

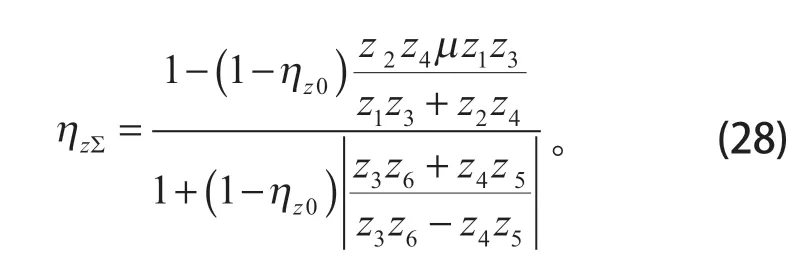
式中：“μ”处，“－”号用于输入、输出轴同向旋转(z3z6＞z4z5)，“＋”号用于异向旋转(z3z6＜z4z5)。

另外，传动装置中，轴承等受力运动组件的损耗，也应按轮系中的承载功率实况进行评估。一般来说，润滑良好的轴承功率损耗要比齿轮的啮合损耗小得多，每个滚动轴承的功率损耗可大致按轴功率的0.1% 粗略估算。

实际应用中，该类超大传动比的传动装置，多以传递运动为首要目标。

4 结语

(1)锥齿轮组成的 2K-H 型行星齿轮装置，行星架可与主轴线呈任意轴交角输出，可适应各种使用需求。ZNGW 型、ZNW 型适合于大范围功率的高效传输，ZWW 型、ZNN 型适用于大传动比齿轮装置。

(2)ZWW 型、ZNN 型锥齿轮行星传动，可实现102～103量级的传动比，但随着传动比的增大，内部封闭啮合功率显著上升，传动效率近似呈反比式急剧下降，不适合中大功率的场合。

(3)锥齿轮组合型行星传动，能实现 104～105量级的超大传动比，可用于输出转动慢似时针的特殊场景；超大传动比仅适用于不考虑机械传动效率而单纯以传递运动为首要目的的场合。