基于静水(冰)压力的闸门构造静力模拟与实验分析探究
夏爱民
(江西省水利水电建设有限公司,南昌 330200)
水工闸门扼守冲水要隘,具有举足轻重的技术和安全意义。本研究参考某山枢纽工程泄洪闸案例,以模拟计算与实验分析的方式,分析探讨静水(冰)压力下闸门构造的静力学承力和工学状态,以期为同类闸门工程设计和建造应用提供参考,助力建设适用牢固的水工闸门工程。
1 案例闸门构造简述
某山枢纽工程共有38孔泄洪闸,其中右岸有10孔,左岸有28孔,每孔宽度20 m。斜支臂表孔弧形为闸门主要方式,其弧形曲率半径R为13 m,主体焊接而成,由双主横梁、斜支臂提供支撑。支铰内置自润滑球面轴承且构造为球面铰。液压启闭机与闸门相接连的吊耳设在下主横梁与边梁相交部位的后翼上。闸门前设置一道检修闸门用来检修与维护。左侧28孔泄控水闸门则由2×1 600 kN液压启闭机操控,液压2×2 000 kN启闭机则用来操控右侧10孔泄控水闸门。闸门的各项参数及主要特点具体见表1。

表1 闸门的各项参数及主要特点
案例闸门构造状态见图1。

图1案例泄控水闸门表孔斜支臂弧形闸门构造示意图
叶门规格:支臂支铰中心距为18.4 m,曲率半径为13 m,孔口高度10 m×宽度20 m,旋转开关角度可达60°
2 建立闸门静力模拟计算模型
2.1 闸门模拟建模
参考闸门图纸规格,借助Solidworks软件实施3D建模,利用ANSYS workbench导入参数进行建模,等轴侧视叶门实体模型见图2。

图2 等轴侧视叶门实体模型
焊接缝在实体建模过程中没有考虑。由于闸门为典型的焊接构造,并且应力集中出现在多个焊接缝中,焊接过程中改变了材质机能,也使周围构造出现突变,此时加大了构造静力模拟分析难度。因此,为方便后面模拟计算及网络划分,本研究利用有限元分析模型对钢板的倒角部分和焊接缝同时进行简化处理。
2.2 闸门热力学材料参数
Q345是一种低合金钢材,也是闸门构造的主要材料,现已在特种设备、桥梁、船舶、建筑等领域实现了广泛应用。其中,345代表钢材屈服强度为345 MPa,Q代表屈服强度。热力学低合金钢Q345参数见表2。

表2 热力学低合金钢Q345参数
2.3 基于壳板构造的壳分析网络划分
闸门各部件为典型的薄壁构造,厚度介于6~25 mm,其主规格均在厚度值10倍以上。此种构造的壳分析可利用ANSYS workbench软件完成,壳体可用Shelll81来模拟。提取各部件的中面,各薄板构件均用中面模型来代替。自动划分网络,100 mm为单元规格,具体见表3。

表3 网络划分参数信息表
2.4 基于静水(冰)静压力作用的边界条件
闸门不执行开启增强动作在结冰期处在常闭状态,因此固定约束两个支臂的最末端,即0是所有方向的自由度。两侧有泄控水闸门固定埋件及叶门底部当作约束及支撑,因此分别移位约束两侧及叶门底部。即Z向约束移位两侧,Y向约束移位底部。
考虑单元数量多,闸门体积大,假如建立一个模型对闸门及冰层的热应力与构造静力进行耦合顺序分析,将大幅增加计算量。为了节省计算时间、提高计算效率,本研究在闸门上部1 m处施加的静冰压力0.118 MPa,并对闸门构造进行分析,由此达到减少计算量、提高运算率的目的。这时冰层的多参数具体见表4。

表4 基于0.118 MPa静冰压力的冰层参数表
闸门的荷载既要考虑静水压力,更要考虑静冰压力。水位表面至闸门的底部就是冰层底面,闸门叶门承受9 m左右的水头释放水压。此荷载的实现完全借助于ANSYSWorkbench中的流体压力施载功能。淡水密度就是流体密度。受闸门止水影响,流体在Y向上有重力加速率,但在X向上没有加速率,因此9 800 mm/s2为流体在Y向的加速率,具体见图3。
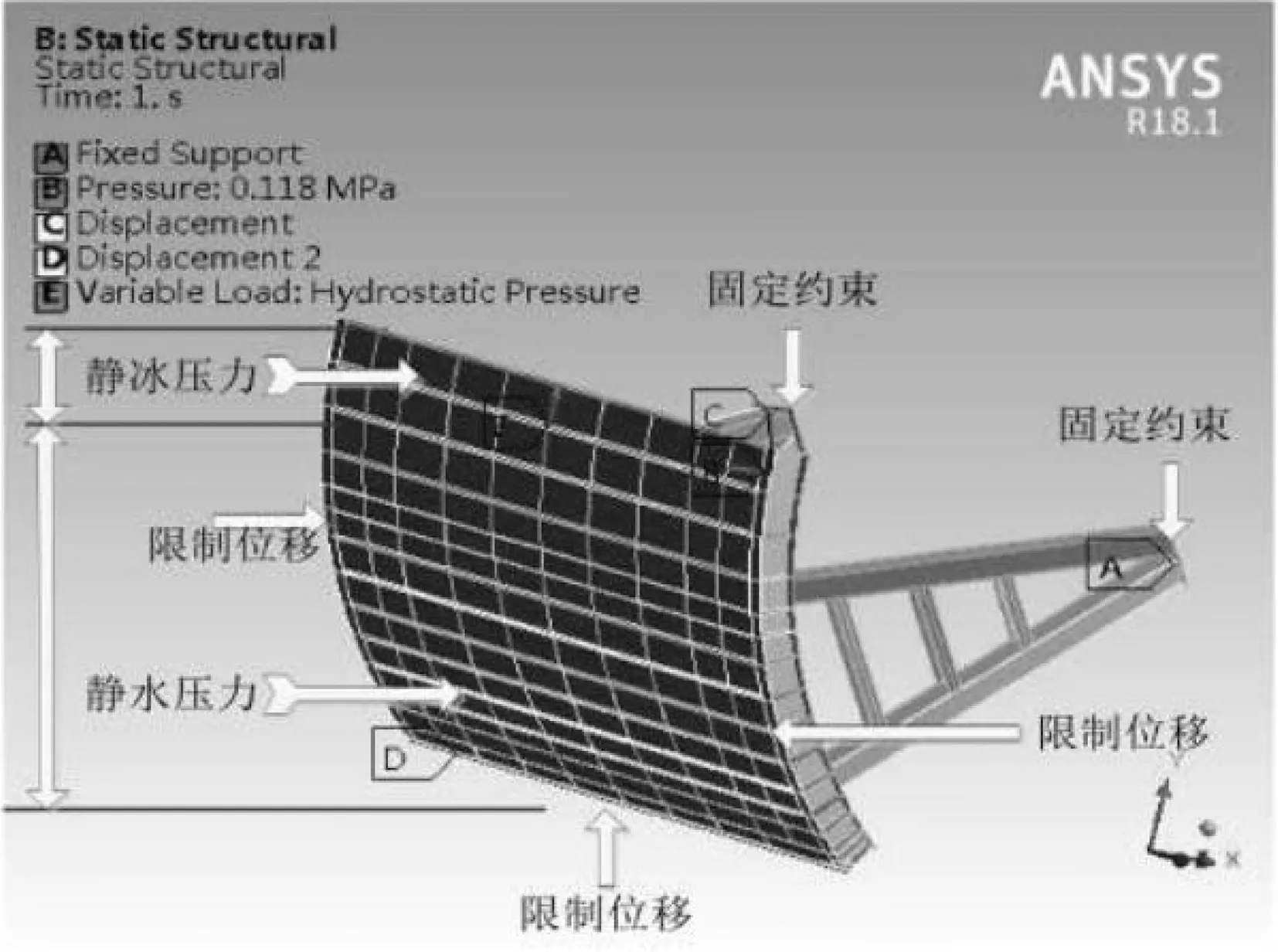
图3案例闸门实体模型荷载和约束示意图
3 闸门应力基于静应力电测法的检测实验
3.1 闸门构造强(刚)度的模拟结果
闸门自身的刚度及强度直接决定其自身的静冰压力承载水平。
闸门厚度值6~25 mm,材质为Q345钢,参考《水利水电工程钢闸门设计规范》(SL 74-2013)整理出与容许应力相关的明细表,具体见表5。

表5 钢Q345容许应力参数
考虑主梁整体弯曲应力及叶门长宽比影响,即便在弹塑性阶段,叶门仍拥有相当大的强度储备。此种现象可通过容许应力与调整常数之积来表达,公式如下:
σ≤1.1a[σ]
(1)
式中:a为弹塑性调整常数,本文中α取值1.5。
利用下式便可确定出叶门强度的正应力:
σ≤1.65[σ]=371.25 MPa
(2)
设计规范规定,0.95为中大型工程中的工作闸门的调整常数值,据此可计算出该闸门的各部件容许应力,具体见表6。

表6 基于调整常数0.95的案例闸门构件应力容许调整值
设计规范要求计算跨度及最大扰度需控制在评判数值以内,由于本研究对象是典型的露顶式工作闸门,故将评判数值定义为1/600,即:
(3)
参考构造图纸,经一系列计算得知,13 200 mm为主梁的计算跨度值,式(3)中带入此值,可计算出最大扰度≤22 mm,即可将容许扰度取值为22 mm。
根据强度方面的判定需求,闸门构造的弹塑性较高,所以第四强度理论更适用于抗弯、抗压及抗拉方面的主应力,即畸变能理论,也被学术界人士命名为VonMises理论,其等效应力值σr4的表达式如下:
(4)
第一、第二、第三主应力关系,即式中的主应力σ1≥σ2≥σ3。因此,要基于第四强度理论确定出等效应力。在抗剪上,需计算出闸门的剪应力最大值。由理论定义进一步发现,等效应力就是最大剪应力,即1/2的应力强度。其等效应力σr3的表达式如下:
σr3=|σ1-σ3|
(5)
由此可求取出剪应力最大值,即:
(6)
在刚度上,主梁最大扰度是首要求解对象,即求取移位形变最大值。整体来看,可通过表7查询出与模拟计算求解的所有内容。
由表7可知,利用第四和第三强度理论,可分别计算出纵梁、主梁、叶门、支臂这四大承压力部件的等效应力,计算成果见图4。

表7 闸门基于刚(强)度的适用理论和模拟求解项


图4 案例闸门强度模拟应力云状态图
0.118 MPa为静冰压力的理想取值,静水压力为高9 m水头的自重压力,固定约束支臂末端,限制移位约束叶门的底部和两侧。对图4中进行梳理,分析结果见表8。

表8 案例闸门强度模拟分析结果
主梁总移位形变见图5。
图5中的数据信息经过转化,结果见表9。

表9 案例闸门主梁刚度模拟结果

图5 案例闸门主梁移位形变云状态图
将刚度与强度这两项指标的模拟计算结果与设计规范标准进行比较后发现,1 m冰厚为闸门的最大承载力,0.118 MPa的静冰压力是在-17℃~-1℃温度区间且持续6 h之后生成的值。另外,所有部件的刚度及强度均比较富裕。
3.2 模拟计算与检测实验结果比对分析
见表10-表12。

表10 案例闸门2012年度结冰期应力检测实验数据 /MPa

表11 案例闸门2013年度结冰期应力实验检测数据 /MPa
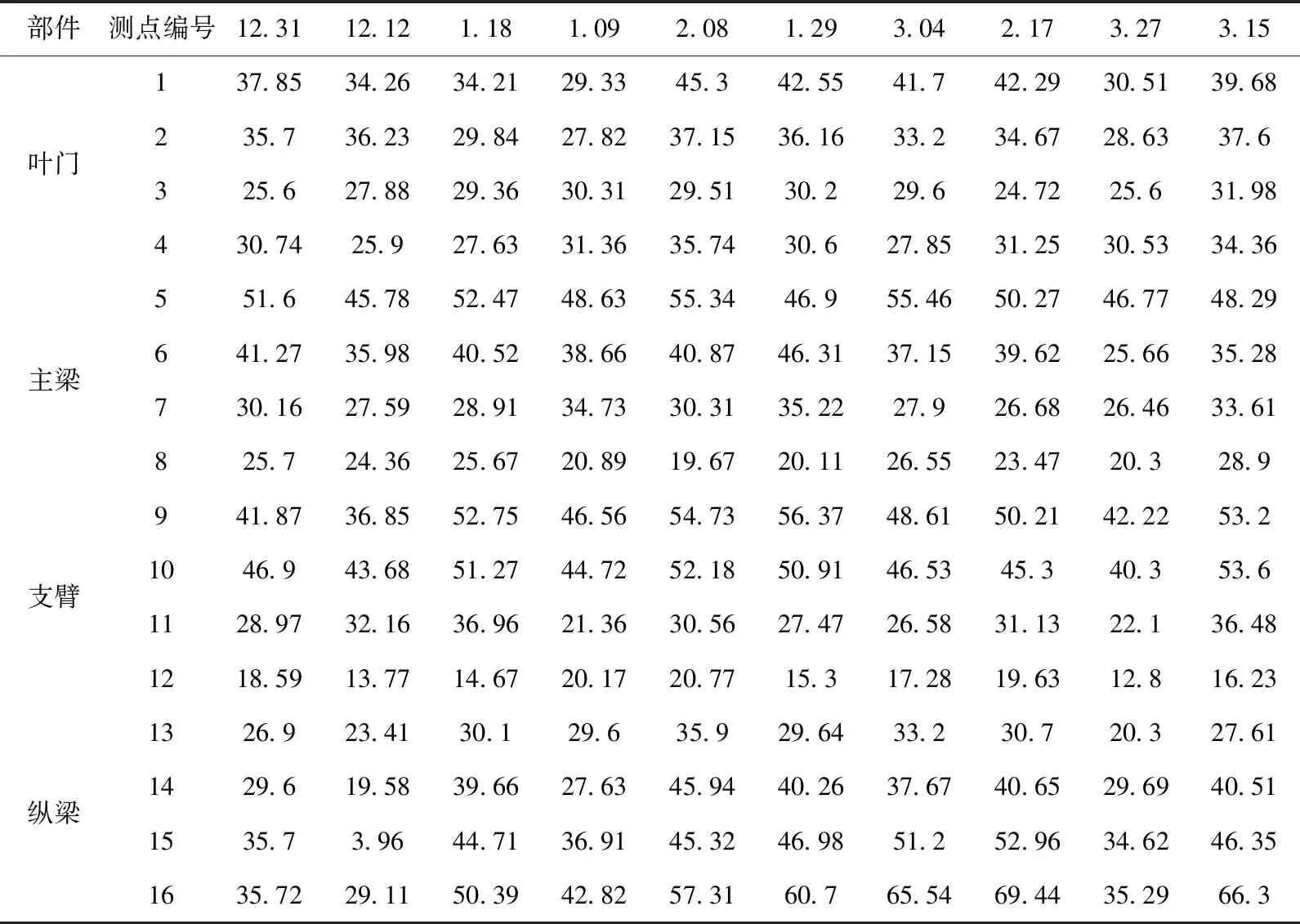
表12 案例闸门2014年度结冰期应力实验检测数据 /MPa
由表10-表12数据分析得知,与其它日期相比,闸门所有部件在2013年3月15日的应力值更大一些。将本研究模拟计算的结果与该日应力检测值进行比较,结果见表13。

表13 模拟计算与静应力电测法检测结果比对
参考误差机理中有关常数的定义有:
(7)
式中:Dξη为数组η间与数组ξ的协方差;ρ为有关常数;σξ、ση为数组η、数组ξ的标准差。
有关常数计算公式(8)是通过展开式(7)生成的,即:
(8)

表13数据揭示,η为模拟值,ξ为应力检测值,利用式(8)计算出有关常数,即ρ为0.86,说明是中度有关。导致偏差的原因:①在模拟计算时,由于各部件的对应测试点与探点取值不能准确匹配,形成取值偏差;②使用静应力电测法时,由于风速、湿度、气候等相关要素影响,无法保证检测结果的可靠性。但结果演变态势未表现出太大差异,说明这两种方法是完全可行的。
4 结 语
本研究以模拟计算与实验分析的方式,对基于静水(冰)压力的闸门构造静力学进行分析,结论如下:①介绍了案例闸门构造,基于案例建立了闸门静力模拟计算模型。②开展基于静水(冰)压力的闸门构造静力模拟计算,并与基于静应力电测法的实验检测结果进行比对分析。③经计算和对比分析得知,0.86为模拟结果与实测值的有关常数,说明两者中度有关,而且它们的演变态势未出现太大差距,证实这两种方法的可行性与可靠性。④经计算和对比分析得知,案例闸门同时承受两方面压力,一是高度9 m水头形成的静水压力力;二是0.118 MPa冰层形成的静冰压力,叶门、主梁、支臂及纵梁是闸门的主承压部件,其等效应力值分别设置为200.63、154.51、134.4及138.54 MPa,最大剪应力分别设置为110.93、88.6、77.4及78.75 MPa。844 mm为主梁的移位形变最大值。其构造的强度与刚度达到规范要求。

