基于径向基函数逼近的波浪折射问题求解

许锡宾，束仲祎，徐绩青,2

(1. 重庆交通大学 河海学院，重庆 400074；2. 重庆交通大学 国家内河航道整治工程技术研究中心 水利水运工程教育部重点实验室，重庆 400074)

0 引 言

波浪在传播过程中，因流场、水深和水位的不均匀变化，海洋情况极为复杂，波浪折射方程始终难以精确求解。近年来，研究波浪折射的方法一般分为3种：① 波射线法，该方法计算简便，容易被工程所接受，但对复杂地形条件计算结果会出现较大误差；② 缓坡方程，该方法适用于水下坡度较缓情况，但对缓坡方程来说，其波浪、海底高度等环境因素必须满足某种条件[1]，其适用范围有所欠缺；③ 有限差分法，该方法作为一种无网格法被用于流体力学方面[2-3]，但由于这种方法需要边界条件，无边界水域情况会降低其求解精度。

笔者通过对波浪折射方程分析，并根据近年来国内外广泛应用的径向基函数几乎可逼近所有函数这一性质[4-6]，将其用于波浪折射方程的求解。通过求解一系列的非线性方程组，可计算出波浪折射的折射角，且求解精度高，能更好地模拟波浪折射问题。

1 径向基函数方法及计算思路

径向基函数利用一个影响范围内每个点与其他所有点的距离来表达它们之间的关系，以径向距离作为变量，是一种具有强大逼近能力的基函数。该函数具有形式简单、各向同性、不依赖空间维数等特点。其基本形式如式(1)：

(1)

式中：y(r)为所用的插值函数；n为指所使用的径向基函数总数目，当节点影响域与求解范围相一致时，一般与节点数目相同，当边界条件有多个时，还会加入辅助函数以提高求解精度；αi为与之对应的i节点的权重系数；║x-xi║为每个节点与第i节点之间距离。

由此可见，径向基函数本质为一个一元函数，具有计算简便，应用广泛的优点，能进行多阶求导，几乎可逼近所有函数，这一巨大优点也是人们应用的重要原因。

笔者主要使用的径向基函数有：Gauss函数和紧支柱正定径向基函数[7]。Gauss函数基本形式为如式(2)：

φ(r)=e-c2r2

(2)

紧支柱正定径向基函数[4]基本形式如式(3)：

(3)

将所求解的空间区域Ω用N个节点(xI,yI)(其中：I=1, 2, …,N)离散，函数α(x,y)在区域Ω中的近似函数αh(x,y)可由一组以各节点(xI,yI)为中心的径向基函数φI(x,y)的线性组合表示，如式(4)：

(4)

式中：aJ为待定系数，a=[a1,a2,…,aN]T；Φ(t)=[Φ1(x,y),Φ2(x,y),…,ΦN(x,y)]T。

将空间区域Ω中的N个节点带入式(4)中，可得到N个方程，联立为线性方程组如式(5)：

Aa=α

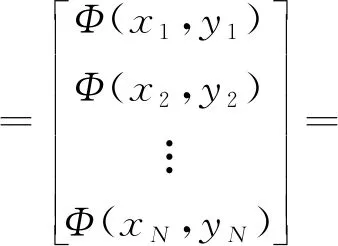
α=[α1,α2,…,αN]T

(5)

将边界条件带入式(6)中，即可得到未知量系数矩阵a。

文中，根据文献[8]提出的精密计算概念和标准，Gauss函数求逆矩阵A-1误差大概是紧支柱正定径向基函数的8倍。由此也可预测出以Gauss函数为基本函数的计算结果精度较低，计算结果明显存在震荡现象。

2 波浪折射方程

在实际海况中，由于波向线与海底等深线斜交，波浪传播方向会发生变化，即产生波浪折射。在波浪由深海向近海岸传播过程中，随着水深变浅，波长、波高和波向等波要素都会发生变化，但是波周期始终不变。忽略风速、风阻、海底摩阻等影响因素，将波浪场视为一个稳定的场[9-11]，其计算如式(6)：

(6)

式中：θ为波浪相位函数；(x,y)为波浪场中任意一点坐标；k为波浪的波数。

在以往对波浪折射问题的计算中，一般都是取边界点的波浪折射角α=0作为边界条件。但该计算方法忽略了边界导数条件，边界点并不符合式(5)，所求出的解并不准确。笔者对于边界点，取α=0。则式(6)可以化简为如式(7)：

(7)

3 算例分析

现有一片水域如图1。水底等高线为同心圆，圆心处高程与静水平面相水平。水域最大半径为3 km，水域内最大水深为-30 m，即最外部水域的水底高程为30 m。现需得出波浪进入此区域1.2 km范围内折射角变化。

由于水域对称分布，故取如图1中水域的一半作为计算区域。为保证边界部分计算精度能达到要求，故取x方向为-3 000 m～-1 500 m；y方向为0～-3 000 m；最后计算结果取1.2 km以内。考虑到编程方便和计算精度，计算区域内取点采用等间距布点，布点间距为25 m。将径向基函数带入波浪折射方程及边界条件方程中，可得到微分方程组，再带入边界条件即可求解。

3.1 算例1

将式(3)作为基本函数，不考虑辅助函数，边界条件取边界点为0，不考虑导数边界条件，计算结果如图2。

此计算结果在边界点位置折射角为0，在边界处存在震荡。由于不考虑导数边界条件，边界处的点不一定满足波浪折射方程导数边界条件，结果存在误差。故此算例证明了导数边界条件的重要性，后续算例都会考虑导数边界条件。

3.2 算例2

将式(3)作为基本函数和辅助函数，边界条件取边界点为0和导数边界条件，计算结果如图3。

此计算结果满足边界点位置折射角为0，同时也满足波浪折射方程导数形式，且计算出的曲面形态较好，无明显震荡现象。该计算方法计算出来的结果是符合波浪折射方程的，为笔者所建议采用。

3.3 算例3

将式(3)作为基本函数和辅助函数，边界条件取边界点为0和导数边界条件，计算结果如图4。

由图4可看出，由于Gauss函数求逆矩阵A-1误差较大，计算结果震荡现象比较严重，存在较大误差，因此这种Gauss函数作为基本函数形式不被采用。

3.4 算例4

将式(3)作为基本函数，式(3)的导数作为辅助函数，边界条件取边界点为0和导数边界条件，计算结果如图5。

此计算结果在局部位置起伏，存在震荡现象，虽然不是很明显，但对计算结果仍然存在影响。计算结果与算例2相比，计算精度有所降低，由此证明该算例所取的基本函数和辅助函数对计算结果存在影响，不建议使用。

4 对比分析

由于算例1中没有考虑导数边界条件，将其边界点计算结果带入式(7)中，求得误差如图6。

为对比分析其他算例计算结果，选择一处相同的计算范围(x轴坐标为-1 940～-2 060；y轴坐标为-1 600～-1 850)，分别截取各算例计算结果局部放大图，如图7。

由理论分析角度来看：在此计算范围中，折射角方向应向右偏转。由图7(a)可看出：算例2计算结果符合理论分析，效果较好；从图7(b)中可看出：算例3计算结果存在较明显震荡现象，计算结果误差较大；从图7(c)中可看出：算例4计算结果趋近于0，即在此范围内其折射角为0，显然不符合理论分析的结果。故笔者选取算例2计算为最终结果，将其与Snell折射定律进行对比分析。

取x轴坐标为-2 500～-1 500 m，间隔取100 m，y轴坐标为-1 500 m，共11个点，运用Snell折射定律计算，如式(8)：

(8)

式中：αi为折射角；ci为折射点处的波速；α0为入射角；c0为入射波速；k为折射点处波数；d为折射点处水深。

图8为Snell定律和算例计算结果的对比。由图8可看出：由于Snell折射定律是特殊情况下的波浪折射，它要求水域内各点水深相同，等深线平行，这种情况与算例实际情况不符合，故其计算结果呈线性。

5 结 论

笔者通过径向基函数和等间距布点方法计算波浪折射时存在的问题。在运用Gauss函数时参考了紧支柱思想，将其中的参数c取值与全局支撑域相关联，为今后Gauss函数运用提供了一种参数的取值方法。但Gauss函数的求逆矩阵A-1误差较大，效果上存在震荡现象，在使用上仍存在一定问题。故笔者的基本函数取紧支柱正定径向基函数和辅助函数取式(3)。

笔者提供了一种计算波浪折射问题方法。在边界点上符合导数边界条件，在理论方面符合波浪折射原理，计算结果更精确，方法更合理。由于Snell折射定律的适用条件特殊，不适用于复杂水深下的海洋环境；而笔者提出的方法则适用于水深变化的波浪情况，为求解波浪折射数值解提供了一种新思路。