基于深度调节方法的集成成像畸变消除

邓莉巾，朴 燕，王 宇，谷岳佳楠

(长春理工大学 电子信息工程学院,吉林 长春 130022)

1 引 言

集成成像技术作为最有前途的裸眼3D技术之一，于1908年由Lippmaon提出[1]。集成成像系统包括元素图像获取阶段和三维重构显示阶段。首先，使用微透镜阵列捕获来自物体不同方向的光线，生成元素图像；然后利用显示设备通过元素图像的反投影显示三维影像[2-4]。集成成像技术的优点是它避免了视觉疲劳的问题，可以实现全视差、连续视点的真三维实时立体成像且无需戴眼镜[5]。近年来，随着电子器件和显示设备工艺的发展，透镜制造工艺愈加成熟，集成成像技术在工程测量、水下成像、三维艺术以及商业广告等方面展现出独特的优势[6-9]。

尽管集成成像技术有许多明显的优点，但仍存在观看视场角窄、景深有限和图像分辨率低等问题[9-12]。目前，已有多种研究方法用于提高景深。文献[13]提出了一个结合图像获取和三维显示过程的深度优先集成成像系统，通过真实和虚拟的图像域显示大景深真三维目标。大连理工大学对多聚焦元素图像进行图像融合，提出了一种提高集成成像景深的方法[14]。四川大学对集成成像显示器中的大景深场景进行任意深度的重新聚焦，实现了景深3D对象的光学重聚焦[15]。这些研究主要是针对三维重构阶段提高景深的，而针对图像采集阶段的研究并不多，且大部分不是用于改善景深的，如文献[16]提出了一种确定最佳采集距离的方法来减少相邻元素图像间的干扰和三维再现过程中的串扰现象。

集成成像的重构阶段也受采集过程中景深的影响，对于固定参数的采集设备，只有在采集景深内的三维场景才能被记录为清晰的元素图像，最终重构出无畸变的三维图像。本文先推导出集成成像系统的目标采集景深模型。参考此模型，通过深度调节的方法，在采集装置固定的情况下，对无法改变位置的深度范围外的三维场景进行深度调节，使得最终的重构效果更加完整，消除了深度范围外目标的重构畸变。

2 理论分析

2.1 采集景深模型

人眼视觉系统具有一定的调节能力，以使清晰的图像聚焦在视网膜上[17]。对于焦平面上的点A和远离焦平面的点B，在图像参考平面上，重建的A点清晰，尽管B点的重建是模糊的，但是人眼视觉系统的调节能力会将B固定在参考平面上。在这种情况下，观察者看到的不是锐利的A和模糊的B，而是一个高亮度的锐利点A和一系列亮度较低的散斑B点，如图1所示。此时B点的重构就是失真的(图中点间距是夸大的，在实际情况下，散点之间的距离小得多)。因此，若想重构出无畸变现象的B点，目标B应在采集景深范围内。

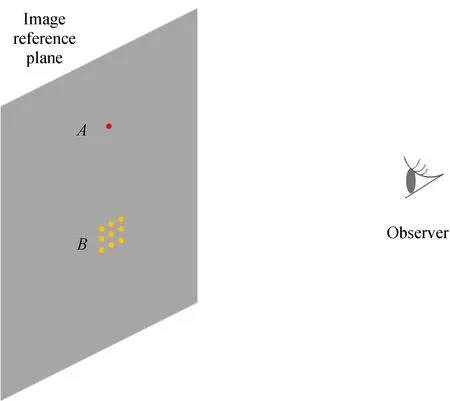
图1 B点的离散现象示意图Fig.1 Discrete phenomenon at point B

集成成像采集阶段如图2所示。三维空间中同一物点经过不同的微透镜，在像面上所成的像点互为同名像点[18-19]。物点A,B分别为聚焦物面上的点，A1-A5和B1-B5分别为A,B经过5个相邻微透镜后在像平面上生成的同名像点。可以看出，物点A的同名像点是锐利的点，物点B的同名像点是散斑，若想观察到清晰的重构图像，三维目标需要在采集景深范围内。图3和图4分别为集成成像采集阶段和重构阶段的单透镜成像光路，这里通过逆向光线追迹进行分析。

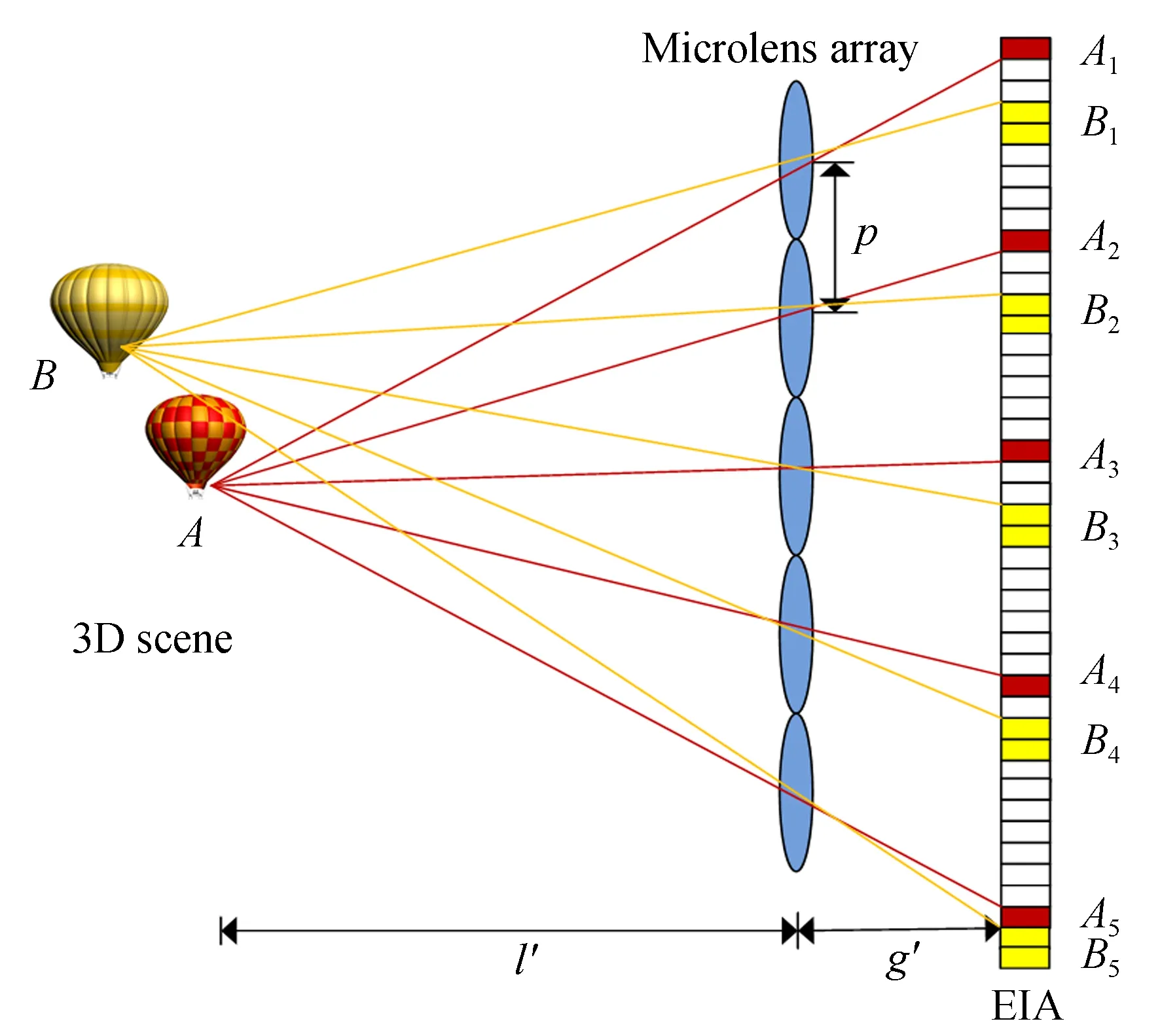
图2 集成成像采集阶段光路Fig.2 Optical path of integral imaging acquisition stage

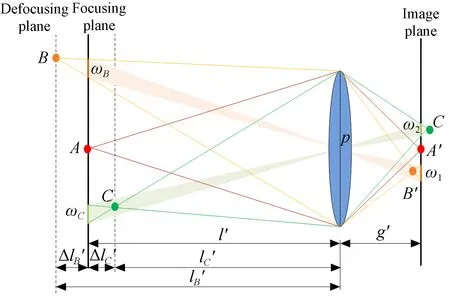
图3 集成成像采集阶段的单透镜成像光路Fig.3 Optical path of single lens imaging in integral acquisition stage

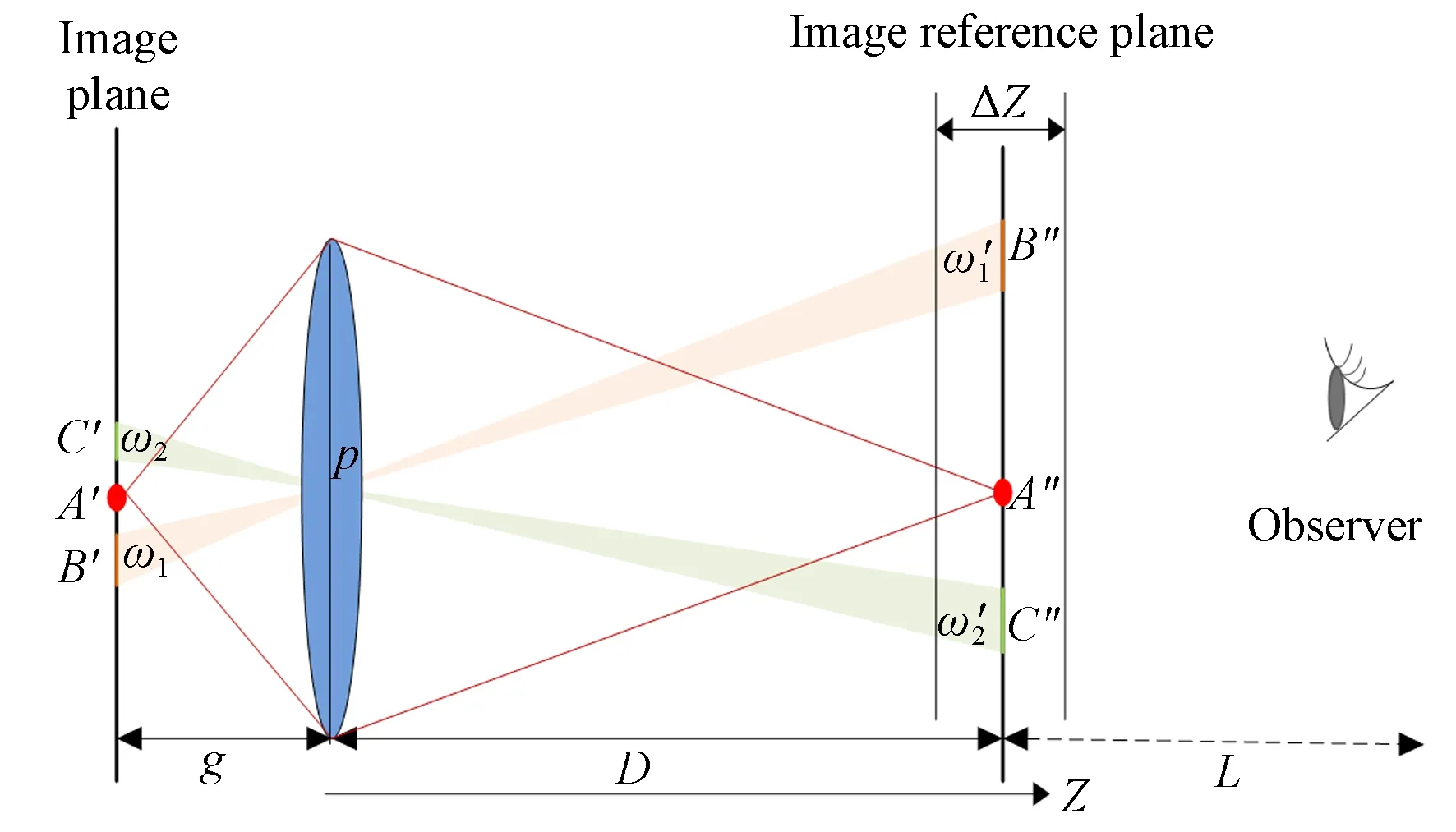
图4 集成成像重构阶段的单透镜成像光路Fig.4 Optical path of single lens imaging in integral reconstruction stage

如图3所示，A点在聚焦物面上，其像点A′在像平面上清晰成像。B点远离聚焦物面，点B在聚焦物面上对应的弥散斑直径为ωB，其像点B′在像平面之外，在像平面上形成的弥散斑直径为ω1，其对应的重构阶段在图像参考平面上的散斑直径为ω1′。根据几何关系可得:

(1)

(2)

采集过程与重构过程的单透镜规格相同，因此g′=g，l′=D，焦距都为f，满足高斯公式：

(3)

推导可得远离聚焦物面的点B的采集距离为:

(4)

远物点B的采集深度为:

(5)

人眼的视场受中心窝和黄斑的限制，在清晰识别时的角度大约为6°～8°。这里取可识别的最大角度8°。当显示图像充满此区域时进行观看，考虑在分辨力和舒适度等方面能得到最佳的观看效果。因此，当画面一定时，可确定图4中的最佳观看距离L为：

(6)

其中φ为显示图像的对角线长。一般情况下，集成成像的图像尺寸与透镜阵列尺寸相等，显示图像与透镜阵列数目一致。对于m×n维数的透镜阵列：

(7)

因此，最佳观看距离L仅与透镜规格相关，当透镜的规格确定时，最佳观看距离也是确定的。在良好的照明条件下，人眼的角分辨率ε为1′～2′，人眼所能识别的最大散斑直径为最佳观看距离与人眼角分辨率之积，即有：

ω1′=Lε.

(8)

代入式(5)可得远物面上B点的采集深度极限为：

(9)

同理可得图3中另一侧远物面上C点的采集深度极限为:

(10)

该系统的采集深度为:

(11)

由此可知，当集成成像采集与重构系统固定时，最佳观看距离也是确定的，采集深度范围与采集距离l′和人眼的角分辨率ε有关，本文取ε=1′=0.000 291 rad。

2.2 深度调节方法

图5为集成成像系统重构阶段的聚焦过程。显示屏上的元素图像阵列(Element Image Array,EIA)发出的光线通过微透镜在中心深度平面处相交，重构的图像具有与原始目标相同的大小和位置，显示屏和中心深度平面互为共轭面，此时的中心深度平面即为重构面(Reconstruction Plane,RP)。最后，人眼将重构面上的图像聚焦在视网膜上，观察者可以通过微透镜阵列看到连续的3D图像。因此，中心深度平面上的计算机重构图像是最接近人眼观察效果的。

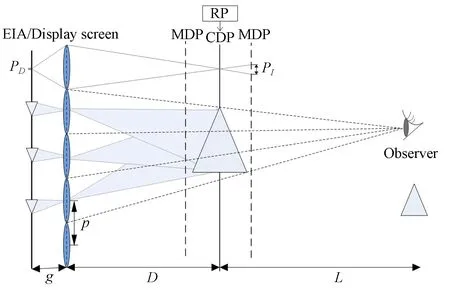
图5 集成成像的重构阶段Fig.5 Reconstruction of integral imaging

集成成像重构阶段的景深范围为中心深度平面CDP到边缘深度平面MDP距离的二倍[20]：

(12)

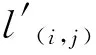
(13)

根据公式(3)的高斯公式可得：

(14)

带入公式(13)得到真实深度Z(i,j)为：

(15)

(16)

为了清晰显示所有像素，重构像素必须位于边缘深度minZ=D-ΔZ/2 和maxZ=D+ΔZ/2之间。因此，真实深度范围为：

Z(i,j)∈

(17)

2.3 结合深度调节的元素图像生成算法

本文使用基于查找表(Look Up Table,LUT)算法的彩色及深度信息生成元素图像，与普通的像素重新映射算法相似，此方法也是利用固定场景得到的彩色图像与深度图像，通过光线追迹进行像素重新映射得到元素图像。然而，集成成像系统受到采集和重构过程中透镜和显示屏参数等的影响，所能呈现的深度范围是有限的，因此对于一些深度范围外的目标，重构时会出现严重的畸变。本文使用的元素图像生成算法的独特之处在于引入了LUT算法后，可以按照系统所能呈现的固定深度进行深度调节，从而改善深度范围外目标的畸变。

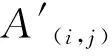
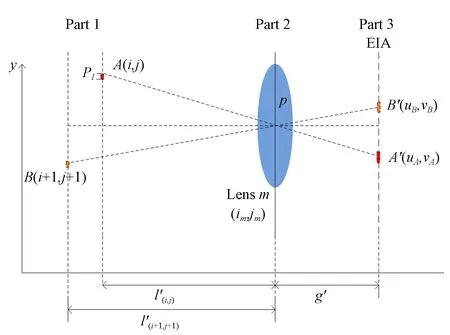
图6 像素映射采集方法Fig.6 Acquisition method of pixel mapping

(18)

(19)

其中：i，j分别是x，y轴上的对应物体像素的序号，im和jm是x，y轴上透镜的序号。通过式(18)和式(19)，可以求出光场中任意一点A(i,j)对应元素图像上的位置A′(uA,vA)，从而得到透镜m对应的元素图像。

图7为物点A在经过透镜m和透镜m+1后在元素图像阵列中的同名像点位移关系，则有：

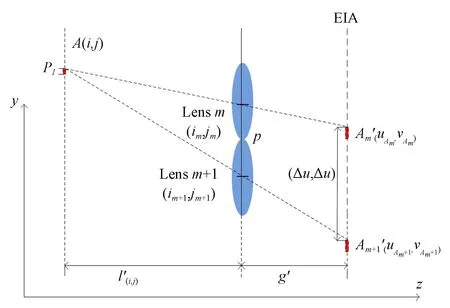
图7 同名像点位移关系Fig.7 Displacement relationship of corresponding pixels

(20)

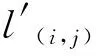
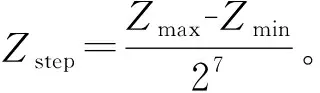
(1)设置LUT模板。像素偏移量为:

(21)

假设输入值为256个灰度值，将LUT的模板设置为S×255，根据像素偏移量得到LUT尺寸为:

(22)

(2)在模板范围内生成LUT:

(23)

(3)将深度图对照LUT进行扫描，按照深度选择区域，获取深度列表后重新进行深度排序，在有效位置返回LUT值。

(4)输出元素图像。经过此算法改进后，根据LUT的返回值得到同名像点的位移关系为：

(24)

参考上文推导出的集成成像系统的目标采集景深范围模型，对此元素图像生成算法进行真实的深度调节，得到可以进行无畸变重构的元素图像阵列，使得三维场景的整体重构效果更加完整，消除了深度范围外目标的重构畸变。

3 实 验

为了验证本文所提的采集景深模型的合理性，采集过程使用3Ds max直接进行微透镜阵列采集元素图像，重构阶段分别进行了计算机仿真重构实验与光学重构实验。在此基础上又设计深度调节实验，该实验分为两组。第一组为3Ds max采集图像的重构实验，采集过程使用3Ds max采集彩色平面图与深度图，使用基于LUT算法的彩色及深度信息生成元素图像后，分别进行了计算机仿真重构实验与光学重构实验。第二组为真实场景相机采集图像的重构实验，采集过程使用真实场景相机采集的彩色平面图与深度图，使用基于LUT算法的彩色及深度信息生成元素图像后，分别进行了计算机仿真重构实验与光学重构实验。

实验使用3Ds max进行图像采集，采集界面如图8(a)所示。重构阶段分别进行了计算机仿真重构实验与光学重构实验。其中，仿真实验采用三维体重构的方法[3]，元素图像不需要进行深度反转；光学实验采用图8(b)装置进行，重构过程使用了厚度为3.3 mm，单透镜孔径p=1 mm的透镜板，透镜焦距为f=3 mm，透镜阵列维度m×n为112×63。本文按照重构过程使用的透镜板的规格设置采集透镜的规格，因此根据高斯公式可得g′=g=3.6 mm，l′=D=18 mm，焦距f=3 mm。使用华为P10手机作为显示屏幕，屏幕分辨率为1 920×1 080，像素密度为432 ppi(pixel per inch)，因此可得像素尺寸PD=0.058 8 mm，参考此屏幕分辨率采集了分辨率为1 904×1 071的元素图像，以尽量充满屏幕。根据公式(6)得到最佳观测距离L=0.92 m，因此使用相机在0.92 m处进行三维成像拍摄，尽量展现人眼的观测效果。表1为实验系统参数。根据表1中的参数及式(9)～式(11)可得系统的采集深度范围Δl′=10.35 mm，远处采集极限距离ΔlB′=6.557 mm，近处采集极限距离ΔlC′=3.793 mm。

图8 光学重构实验装置Fig.8 Experimental configuration for optical reconstruction

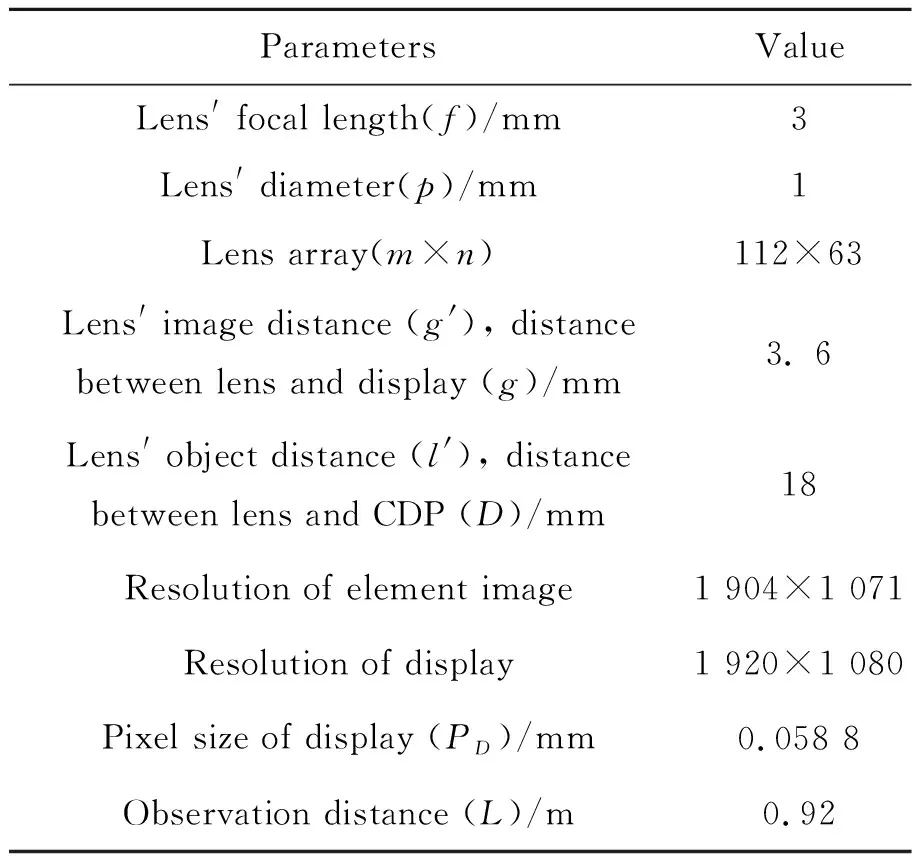
表1 实验参数

4 实验结果与分析

4.1 采集景深模型验证实验

仿真实验使用3Ds max直接进行元素图像的采集，根据公式(16)得到集成成像系统的无畸变采集距离l′为14.207～24.557 mm。参考此采集景深范围，将透镜阵列和三维模型按照图9所示排布，采集两组元素图像。第一组中字母AC在采集景深范围外，第二组中所有三维目标均在采集景深范围内的。这里字母间距设置较小是为了验证本文所得采集景深模型的准确性。图10分别为这两个三维场景在中心深度平面D=18 mm处的计算机重构示意图。从图中细节的放大部分可以明显看出，第一组的字母AC在采集景深范围外，重构图像畸变严重，第二组所有字母都在采集景深范围内，重构图像清晰。图11为光学实验结果，光学实验结果与仿真结果一致，进一步验证了本文所提采集景深模型的合理性。图10细节部分图像的能量与光强分布如图12所示，客观表现了在采集景深范围内字母的重构图像轮廓清晰，模型边缘平滑，重构图像无畸变。在此采集模型下获得的元素图像阵列都是清晰实焦的，皆在重构成像的深度范围内。

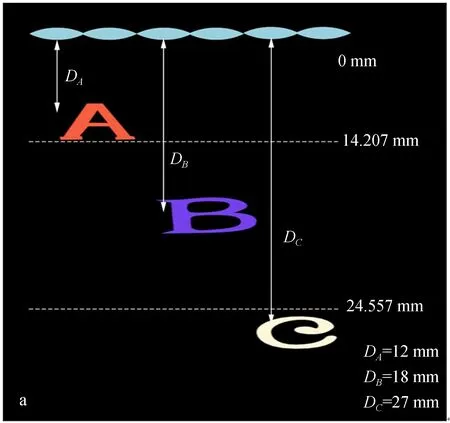
图9 三维场景排布Fig.9 Arrangement of 3D scene

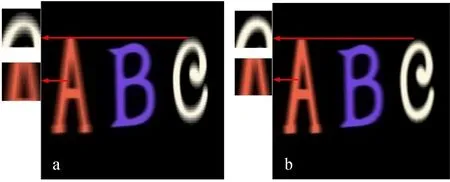
图10 在中心深度平面处图9的计算机重构图Fig.10 Reconstructed images of Fig.9 at center depth plane

图11 光学实验结果Fig.11 Results of optical experiments

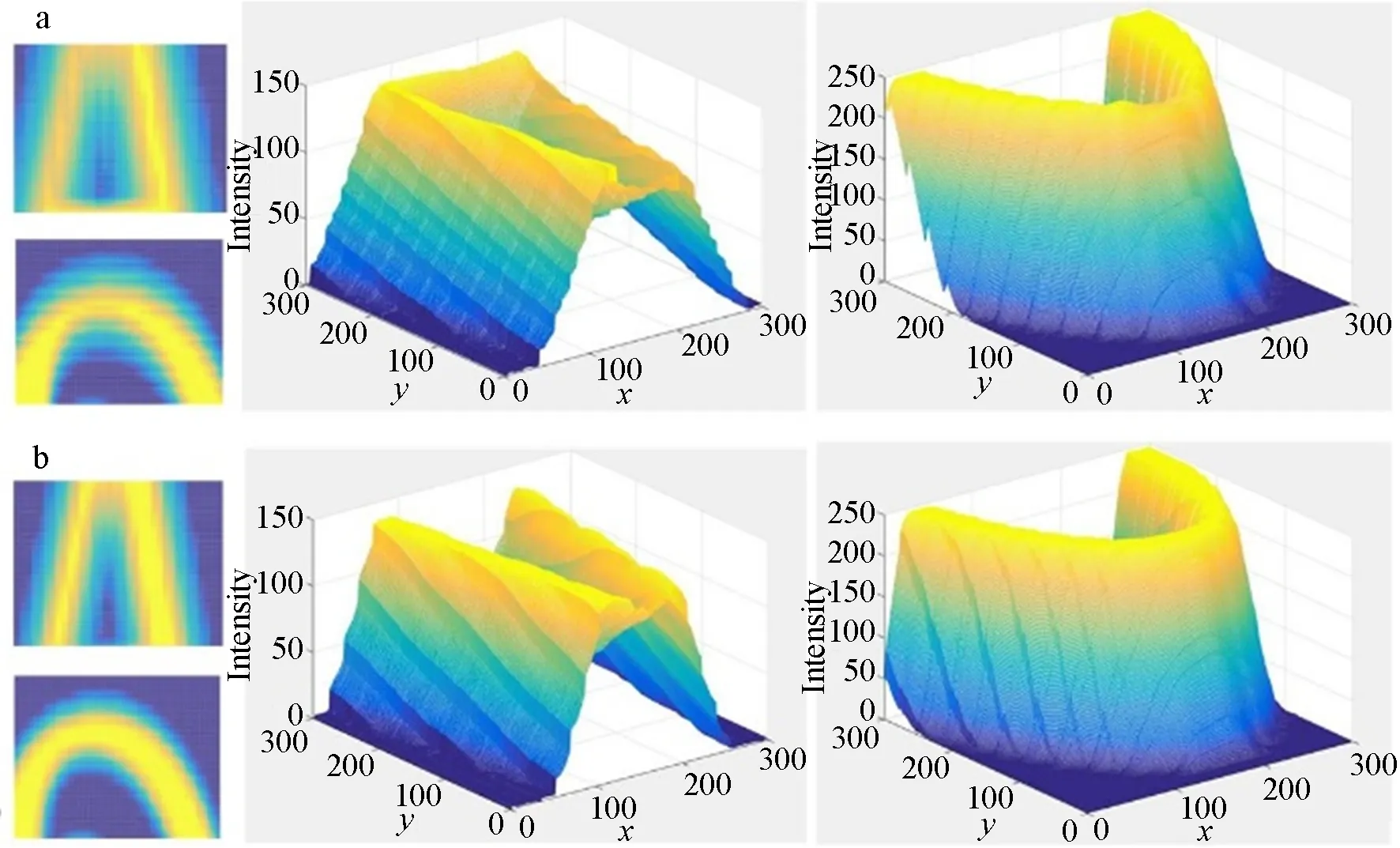
图12 重构图像细节处能量与光强分布Fig.12 Distribution map of energy and light intensity at details of reconstructed images

4.2 3Ds max采集的无畸变重构实验

由于集成成像系统的采集距离l′在14.207～24.557 mm的三维目标可以无畸变重构，在此采集范围内，根据公式(17)可得无畸变深度Z为13.193～22.805 mm。参考此深度范围做深度调节，设计深度调节实验，基于LUT算法的彩色及深度信息生成元素图像，在此过程中，参考所得的无畸变深度Z进行深度调节。图13为生成元素图像阵列所用的彩色图及元素图。3Ds max是专业的计算机三维图像应用软件，使用3Ds Max 拍摄彩色图与深度图，像素数皆为800×800，使用焦距为150 mm的相机，在距离目标100 mm处进行模型的拍摄，并在同一位置将模型转化为黑白深度图，得到图13中的彩色图和深度图。模型中字母间距为25 mm，字母间距设置较大是为了验证本文所提深度调节方法的广泛适用性。利用图13的彩色及深度信息生成两组元素图像，分别生成无深度调节的元素图像，即ΔZ=50 mm；和本文提出的无畸变深度调节方法所得的元素图像，即ΔZ=9.6 mm。生成的元素图像如图14所示。它们在中心深度平面处的体三维重构的计算机仿真图如图15所示。可以看出，经过无畸变深度调节后，字母X与Z的畸变现象得到了明显改善，图16的光学实验结果也与此一致。分别将图13中的平面彩色图与图15两组计算机重构图像进行客观评价实验，经过深度调节后，重构图像的颜色直方图相似度(CHS)从67.057%提升到94.507%，如图17所示。另外计算图13中的平面彩色图与计算机重构图像图15(a)的结构相似性(SSIM)为54.002%，峰值信噪比(Peak Signal to Ratio,PSNR)为16.902，与图15(b)的SSIM为84.510%，PSNR为19.740，可以看出经过深度调节，重构图像的结构相似性明显提高，峰值信噪比变大，图像畸变减少。

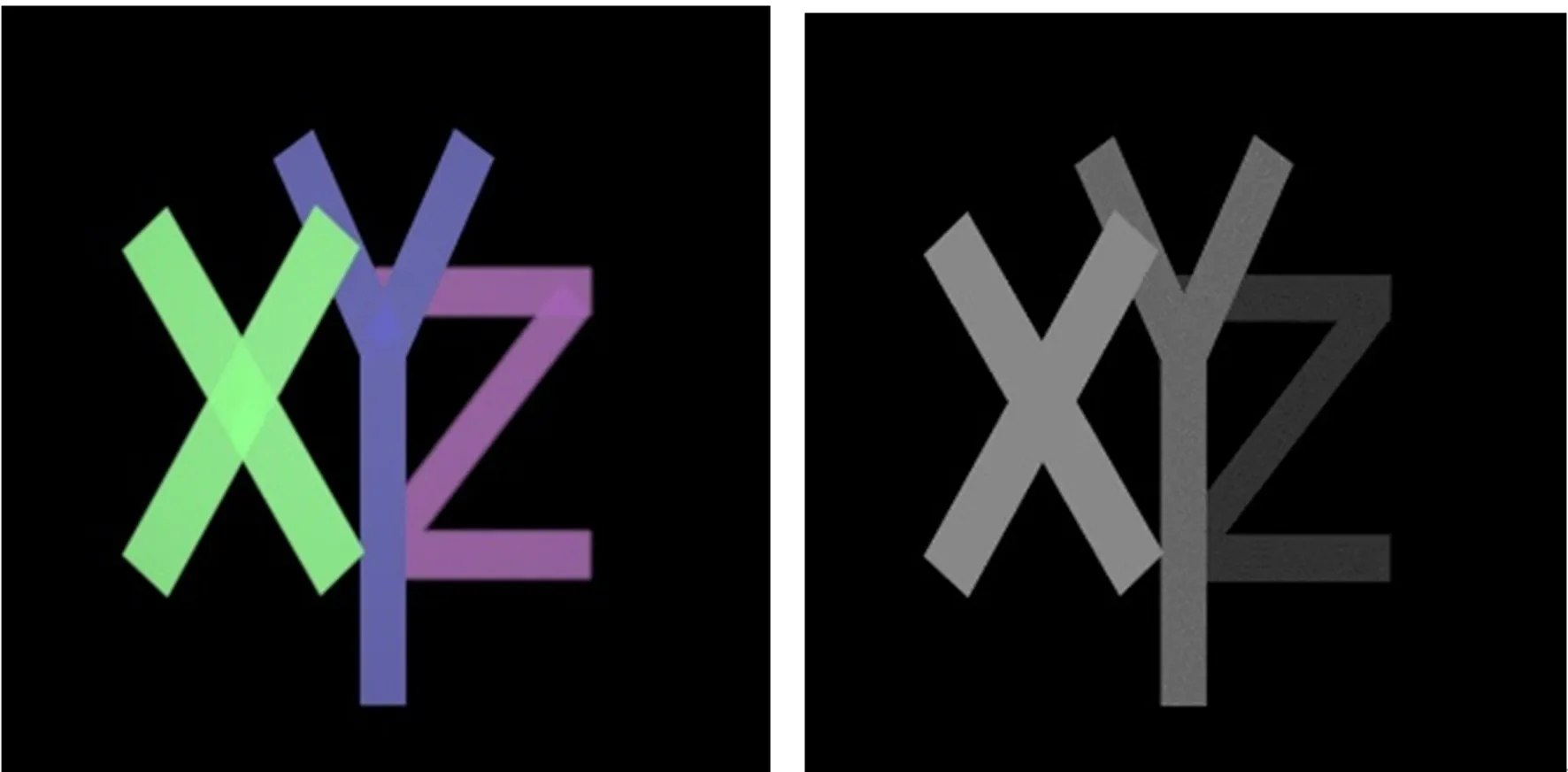
图13 实验采集的彩色图及深度图Fig.13 Color and depth maps collected by experiments

图14 生成的元素图像Fig.14 Generated EIs

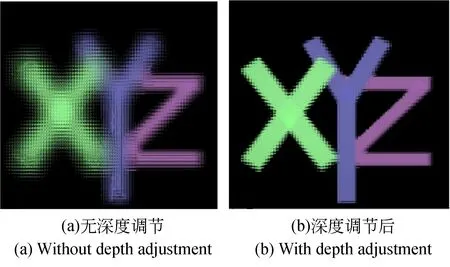
图15 在中心深度平面处计算机重构示意图Fig.15 Reconstructed images at center depth plane

图16 光学实验结果Fig.16 Results of optical experiments

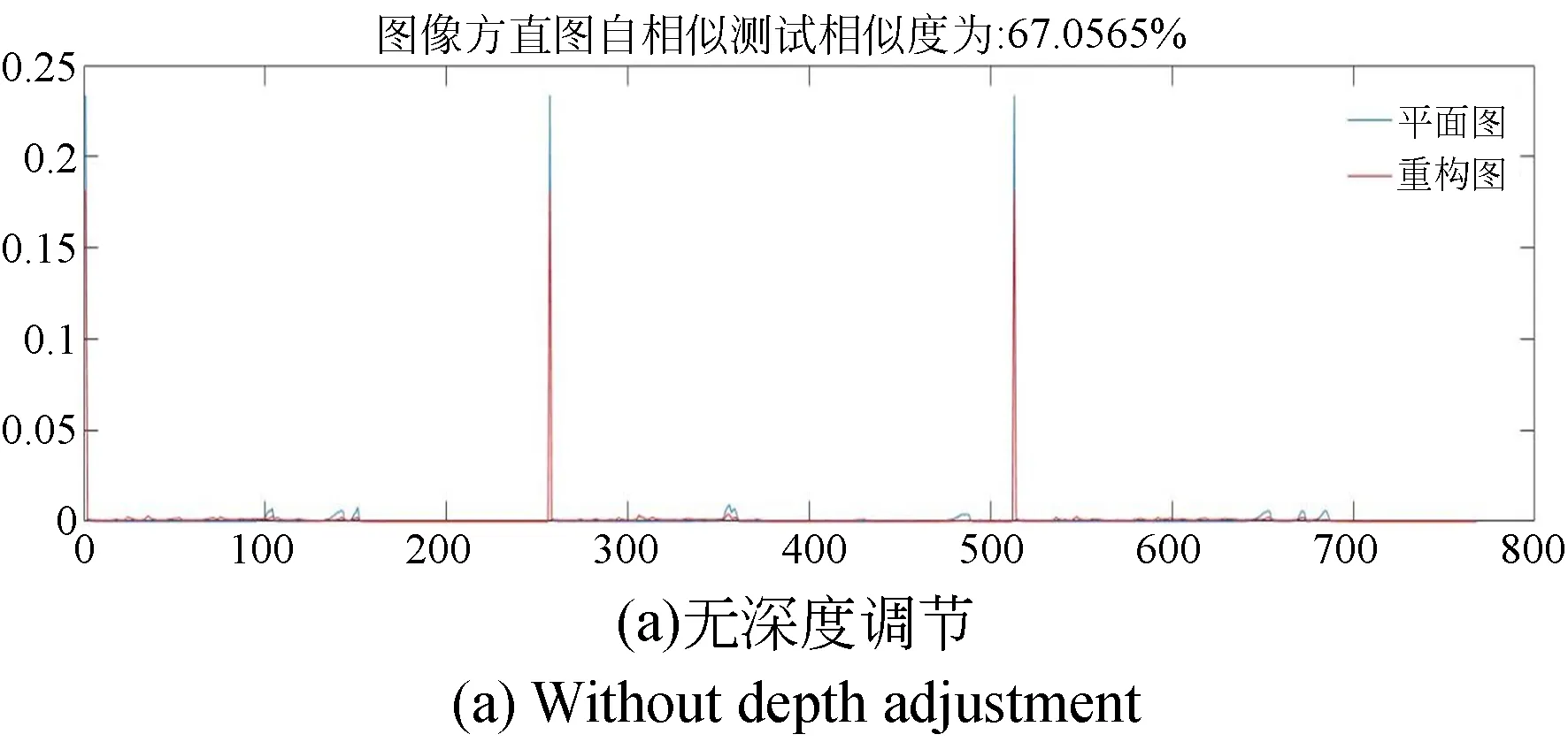
图17 计算机重构图与彩色图的颜色直方图相似度Fig.17 Histogram of color similarity with color map and computer reconstructed image

4.3 真实场景的无畸变重构实验

为了更进一步说明此方法的实用性，这里加入一组真实场景的重构实验。实验场景的彩色图与深度图如图18所示，使用的是Microsoft公司的MSR 3D视频数据集中一幅芭蕾舞场景的彩色图与深度图[22]，分辨率皆为1 024×768。

图18 彩色图及深度图Fig.18 Color and depth maps

本文所提的方法适用于大景深场景的三维重构，然而目前已经提出的元素图像生成算法大部分都是针对小场景的三维目标。图19所示为使用文献[23]方法得到的两种元素图像，它们的计算机重构效果和光学实验结果分别如图20和图21所示。可以看到，无论是场景前方的男人还是场景后方的女人，重构效果都比较差，因此这两种方法对于大景深的三维场景重构效果不佳。

图19 生成的元素图像Fig.19 Generated EIs

图20 计算机重构示意图Fig.20 Reconstructed images

图21 光学实验结果Fig.21 Results of optical experiments

此集成成像系统无畸变重构的采集距离l′在14.207～24.557 mm，无畸变深度Z在13.193～22.805 mm。基于LUT算法的彩色及深度信息生成元素图像，在此过程中，参考所得的无畸变深度Z进行深度调节。利用彩色及深度信息生成两组元素图像，分别为不做深度调节的元素图像，和本文提出的无畸变深度调节方法所得的元素图像，即ΔZ=9.6 mm，如图22所示。通过像素提取方法对两幅元素图像进行计算机重构，得到的两组计算机仿真重构图如图23所示，可以看出，经过无畸变深度调节后，重构效果明显变好，尤其远处舞者的畸变现象得到了明显改善，图24的光学实验结果也与此一致。实验表明，与无深度调节的方法相比，基于深度调节方法生成的元素图像的重构效果明显消除了畸变现象。除此之外，与文献[23]相比，本文提出的方法更适用于大景深场景的三维重构。

图22 生成的元素图像Fig.22 Generated EIs

图23 计算机重构示意图Fig.23 Reconstructed images

图24 光学实验结果Fig.24 Results of optical experiments

表2分别比较了这4种元素图像生成方法的计算机重构图像颜色直方图相似度(Color Histogram，CH)、结构相似性(SSIM)和峰值信噪比PSNR。可以看出，本文经过深度调节得到的重构图像的结构相似性明显最高，峰值信噪比最大，图像畸变减少。

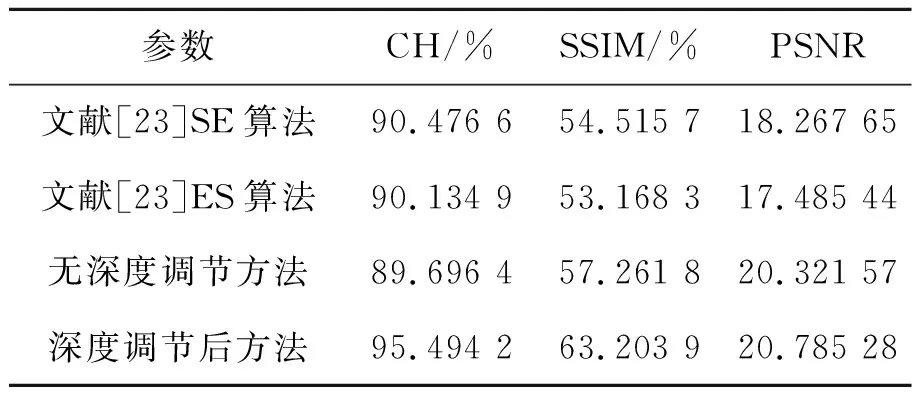
表2 客观评价实验结果

5 结 论

本文在人眼视觉特性和集成成像的光线追迹分析基础上，提出采集景深范围模型；以此模型作为指导，推导出集成成像的真实深度范围；针对在采集景深范围外的目标，其重构深度超出了真实深度范围，因此又提出通过参考真实深度范围进行深度调节的LUT元素图像生成算法，来实现整个三维场景的完整重构。本文提出的采集景深模型和深度调节方法，对参数固定的采集设备，在无法改变三维场景中目标位置的情况下仍可以进行整体的无畸变重构，并且重构轮廓清晰，提高了集成成像的整体观察效果。这种方法虽然牺牲了景深，但可以为场景外的目标提供更清晰的再现像，不受采集装置和目标场景限制，可广泛应用于分辨率优先的集成成像显示系统。