基于Laplace变换的潜水非稳定流模型解的研究
刘 能 胜
(湖北水利水电职业技术学院,武汉 430070)
0 引 言
河渠水位的变化是影响两岸地下水动态的重要因素,对河渠间潜水的非稳定运动规律的研究,对区域地下水资源评价、灌排渠系设计、地下水动态预报都有着重要的意义[1-4]。其中,地表水体附近潜水非稳定流与渗流规律研究[5-11]已在渠道附近地下水动态过程研究[12-15]中得到广泛应用。
在之前的研究中,假设河渠完全切割潜水含水层,将河渠视为第一类边界的河渠—半无限潜水非稳定流模型,大体分为两类:①河渠水位变化瞬时完成并保持稳定[1-4],对于这类简单的边界条件函数,可利用常用的积分变换方法,求出模型的理论解;②河渠水位持续变化[1,3,5,6],对于这类问题多将水位的变化过程概化为一常规函数,如线性变化,当函数形式较为简单时,也可以通过常用的积分变化方法进行模型求解。对于上述两类问题现已有较为深入的研究,但实际情况中,河渠水位多难以一已知函数形式进行概化,即便某些特定条件下可给出变化过程的具体函数形式,但当函数过于复杂时[10],其常用的积分变换方法便难以进行模型求解。
后来的研究中为解决复杂函数边界的河渠—半无限潜水非稳定流模型问题,吴丹[16]等利用傅里叶变换方法对所概化的复杂函数边界进行处理,并给出了该边界条件下模型解,但其求解过程过于复杂,且并未验证解的正确性,而且在实际情况中,其河渠水位变化过程多为一未知函数,故对未知边界函数形式条件下的河渠—半无限潜水非稳定流模型问题进行相关研究具有实际意义。
针对上述情况,本文采用不考虑边界条件形式的Laplace变换方法求解,利用Laplace变换中的有关性质,给出模型的解,并与数值解进行对比验证;同时为了进一步讨论该理论解在实际中的运用,本文对河渠水位变化过程采用Lagrange插值进行离散化处理,并借助文献[16,17]中的算例数据进行验算,对其应用展开介绍。
1 经典模型及其解
为研究河渠附近潜水非稳定运动,对河渠及附近地段的水文地质条件作如下假设:①潜水含水层均质各向同性,隔水底板水平、平面上无限延伸;②河渠顺直且在剖面上完整切割含水层,河渠水位变动过程为时变函数H(t);③潜水初始水位h(x,0)与河渠水位水平、潜水水流可视为一维流;④忽略上部入渗量,不考虑垂向交换作用。
上述水文地质概念模型,可写成数学模型(Ⅰ)。
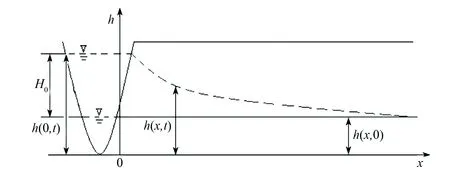
图1 河渠附近潜水的非稳定运动Fig.1 Transient phreatic motion near rivers and canals
式中:μ为潜水含水层给水度;H为潜水水位,m;K为含水层渗透系数,m/d;H(t)为河渠水位随时间变化函数,m。
在经典模型中,H(t)=H0,H0为常数,即“河流水位在迅速升高H0后,保持不变”。当含水层厚度较大时,水位变化h(x,t)-h(x,0)≤0.1hm(潜水流的平均厚度,即研究时段始、末潜水流厚度的算术平均值)时,根据Boussinesq方程第一线性化方法,模型(Ⅰ)可改写成(Ⅱ)。
(Ⅱ)中:u(x,t)=h(x,t)-h(x,0),a=khm/μ,a,(m2/d)为潜水含水层的导压系数。
当H(t)=H0,利用Laplace变换,可获得上述模型的解:
(9)
2 理论模型
2.1 理论模型的求解
实际中的河渠水位变化过程H(t),虽在小范围流域内有一定的规律,但由于外界干扰因素过多,其变化过程更具随机性,再加灌区人工干扰因素,基本无法对水位变化过程进行统一的具体函数表达,在此条件下,本文在不追求H(t)的具体函数形式基础上,建立不依赖边界函数的变换过程的Laplace变换方法,求解这类模型的理论解。
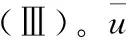
对于模型(Ⅲ),当式(11)过于复杂或未知时,难以采用上述方法直接求解,对此,针对式(11),不直接求H(t)的象函数,而只将其以算符的形式运用于计算过程中,再利用变换的相关性质和相应的特征函数,进行求解。详解过程如下。
(Ⅲ)中(10)式的通解为:
(13)
式(13)中,λ1、λ2为待定常数;由边界条件(11)和(12),模型(Ⅲ)的特定解为:
(14)
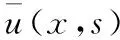
(15)
式中:*为卷积算符。
参照常用Laplace变换中的函数:
对式(16),根据Laplace变换的“微分定理”,有:
(17)
其中:
结合式(15)、(17),有:
(18)
对式(18),将卷积打开,注意h(x,t)和u(x,t)的关系可得:
式(19)即为不考虑H(t)的具体函数形式下模型(Ⅱ)的解;在实际问题的运用中,还需将具体的H(t)代入到式中,进一步换算,才能得到实际问题的解。
对于式(19),其河渠水位变化过程以H(t)进行概化,而之前的研究中多以一已知常规函数进行处理,但在实际中,河渠水位的变化多难以函数形式进行概化,即便存在,也多为一些非常规函数,给求解带来了极大的困难,而本文通过对Laplace变换性质的运用,避免了边界函数的变换过程的复杂性,进一步推动了经典模型的解在实践中的运用。同时需要指出的是,上述求解过程中,边界条件H(t)虽未进行形式上的变换,但其实际参与了Laplace变换与逆变换的过程,所以,H(t)应满足Laplace变换要求,在实际中,河渠水位变化基本是可以满足变化要求的。
2.2 解析解与数值解的对比分析
为了进一步探讨解析解的正确性以及与模型数值解的区别,本文以下述应用中文献[17]中的实例为背景,利用基于有限差分的GMS软件[18]对河渠附近地下水进行数值模拟,将河渠作为第一类边界处理,垂向上为与解析解概化一致,只设置一层,并对潜水一维稳定流的数值解与解析解的计算结果进行比较,计算模型概化中,河渠水位变化过程如表2所述,各参数取值为给水度μ=0.04,渗透系数k=4.26 m/d,计算不同时刻河渠附近地下水位情况。
图2为河渠水位变化24 h末的数值解和解析解的比较。
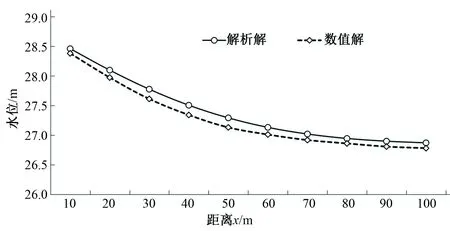
图2 24 h末河渠附近地下水位Fig.2 24 h-end Water Table Near Rivers and Canals
从图2可以看出,至24 h末,河渠附近地下水水位的数值解和解析解存在一定误差,经分析,解析解与数值解的偏差率为0.03%,平均相对误差为0.4%,通过分析解析解求参运用及与数值解的对比可得:
(1)当实际水文地质条件较为简单时,在合理概化的基础之上可以直接采用解析法来求取水文地质参数并预测地下水动态。
(2)解析解在野外实际运用时,可以提供一个简洁的估算方法,也可以利用其所得结果进一步指导勘探和野外试验工作。
(3)对本文所述的理论模型来说,解析解是精确解,可以用来检验数值解法的正确性和比较不同数值解法的精确性和有效性。
同时,解析法的局限性也非常明显,它不能适用于含水层的各种复杂条件,因此将它利用于实际计算时不可能得到精确的结果,但作为一种进行理论研究和初步估算的工具来说,具有重要的意义。
3 运 用
3.1 Lagrange插值
实际中,复杂的河渠水位变化过程H(t),显然难以给出统一的数学表达式;在之前的研究中,多将河渠水位变化过程多概化为阶梯状分段函数,但在实际情况中河道水位的变化应是连续的,阶梯状的河道水位变化过程难以出现,因此,为使河道水位变化过程的概化的实际意义更加合理,本文采用Lagrange插值方法[16,19],对H(t)进行离散化处理;
对于时段Ti=ti-ti-1,有:
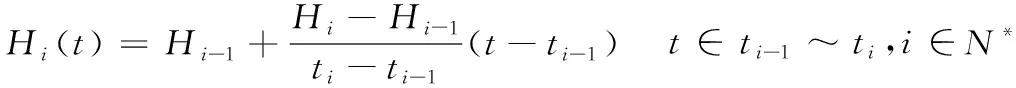
(20)
则有:
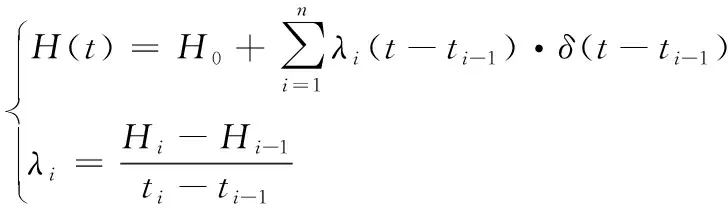
(21)
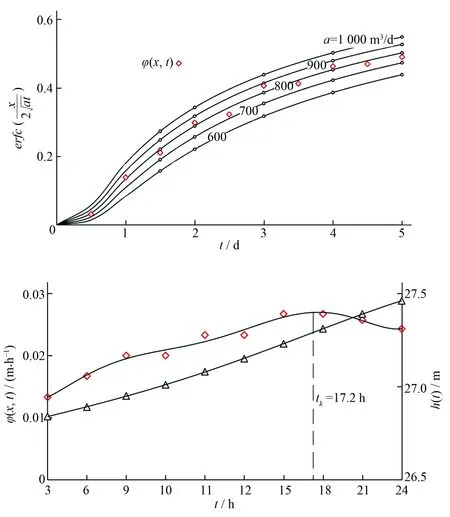
δ(t-ti-1)系Heaviside 函数,具有如下性质:当t 在吴丹、陶月赞[16,17]等有关河渠附近潜水非稳定流的研究中,提出了“配线法”和“拐点法”的参数求解方法,推广了解析解在实际中的运用,本文将基于上述两种方法,结合相关实例探讨本文所求解析解在实际中的运用。 设潜水位变动速度φ(x,t)=∂h(x,t)/∂t,注意u(x,t)=h(x,t)-h(x,0),结合卷积定理的微分特性,由(18)式: (22) 结合式(21),注意,当t=0时,H(t)=H0及Heaviside 函数的性质,得: (23) 3.2.1 配线法 对于式(23),当H0=0∩λ≠0时: (24) 需要注意的是,配线法在实际运用时,要求河渠初始水位基本保持稳定,这样从模型概化的角度出发即可认为H0=0。 3.2.2 拐点法 对于式(22),当H0=0∩λ≠0时,对φ(x,t)关于t再进行一次求导,并令∂φ(x,t)/∂t=0,求出相应拐点; (25) 令拐点处的时间为tk,有: (26) 根据距边界x处的地下水水位动态,绘出∂φ(x,t)/∂t~t曲线(此时,x是一确定值);利用曲线的拐点tk,以及河渠水位实际变动数据而获得的H0、λ;由(26)式,可计算出含水层参数a,需要注意的是,拐点法应用时要求河渠初始水位要有个迅速的变化过程,这样从模型概化的角度出发即可认为H0≠0。 河渠与潜水之间的补排关系,由河渠水位与潜水水位关系所决定,这也表明,河渠附近潜水非稳定渗流模型,可以用来计算河渠与潜水之间的水量交换;其中,河渠与潜水之间的交换量,可以用单位河渠长度上的交换量表达,即单宽流量q(t);t时刻的交换强度q(t),由达西定理: (27) 如前文,在实际问题的运用中,还需将具体的H(t)带入到式中,进一步换算,才能得到河渠与潜水之间的水量交换计算公式。若H(t)采用Lagrange插值进行离散化处理,根据式(27)可得: (28) 式(28)即为河渠与潜水之间在t时刻的交换强度算式;q(t) >0,表示潜水接受河渠补给;q(t)<0,表示潜水排泄河渠。 本文以文献[16,17]中算例数据进行参数计算。根据文献所述,安徽淮北平原中部的蒙城县境内茨淮新河灌区潜水含水层广泛发育,厚度8 m左右,其下发育有不完全连续黏性土隔水层;潜水位埋深多较浅;且农业区内灌渠系统较完善,灌渠之间的间距多为2 km左右,干渠渠首大部分建设有节制闸;区内有一口国家级地下水位自记观测井,距离干渠距离约为60 m,观测井附近地面标高31.02 m。 据文献[16]表述,2014年7月下旬,由于未处于运行期,干渠水位基本长时间保持不变,符合“配线法”中要求的H0=0;且该时段为无雨期,计算中忽略垂向交换作用;可采用配线法进行求参;数据摘录如表1。 据文献[17]表述,2013年8月26日15时至27日15时,干渠节制闸关闸蓄水;其水位变化过程可分为两个过程,关闸15 min内,水位迅速上升2.00 m,随后,水位上升速度减缓,至27日15时升幅为0.21 m。观测孔水位摘录如表2。该时段,H0=2.0 m、λ=0.21 m/d,满足拐点法要求的求参条件,可采用拐点法求参数。 由图3可见,配线法中,实测散点数据基本处与a值为700~900 m2/d,因此a值可取800 m2/d;对于拐点法,其潜水位达到最大变动速度时所对应的时间十分靠近18 h,故拐点取tk=17.2 h,按式(26)求得a=851 m2/d。 表1 潜水水位动态数据(2014.7.25-2014.7.30)与“配线法”计算过程Tab.1 The dynamic data of water table (2014.7.25-2014.7.30) and calculation process of “Curve Fitting Method” 表2 潜水水位动态数据(2013.8.26-2014.8.27)与“拐点法”计算过程Tab.2 The dynamic data of water table (2013.8.26-2014.8.27) and calculation process of “Inflection Point Method” 图3 配线法及拐点法求a(x=60 m)Fig.3 Calculate a(x=60 m) by means of curve fitting and inflection point methods 根据文献[16,17]的研究成果,采用配线法及拐点法求得参数a值分别为890 m2/d和860 m2/d,与本文所求结果基本一致,但仍存在一定差异,其主要原因为: (1)上述两方法在最后配线及拐点位置确定时均为人为估计,难免会产生一定误差; (2)本文进行参数求解与上述文献进行参数求解时所依据的理论模型及解析解有所区别,具体表现在对河渠水位边界形式概化上。 本文通过采用不考虑边界条件形式的Laplace变换方法对未知函数边界条件下的河渠—半无限潜水非稳定流模型进行求解,并与数值解进行对比验证,同时展开了相关应用的探讨,得出以下结论: (1)针对半无限域河渠附近潜水非稳定运动经典模型中河渠水位边界条件概化的局限性,本文采用不考虑边界条件形式的Laplace变换方法求解,可得到形式较为简单的解析解,此外,Laplace变换在模型求解中可避免边界条件函数变化所带来的象函数求逆的困难,对于未知边界函数的模型求解有着重要的意义。 (2)河渠水位变化过程往往比较复杂时,利用Lagrange插值的方法对河渠水位过程进行离散化处理,同时利用配线法及拐点法进行参数计算,参考相关文献,结果基本一致,方法可行,此外,插值函数的基础上,推导了河渠与潜水之间交换量计算,可为实际问题求解提供更简便的途径。 (3)对比数值解和解析解可以发现,当实际水文地质条件较为简单时,在合理概化的基础之上可以直接采用解析法来求取水文地质参数并预测地下水动态,但需要注意的是解析法的局限性也非常明显,它不能适用于含水层的各种复杂条件,此外模型是建立在一维概化的条件下,因此将它利用于实际计算时不可能得到精确的结果,但作为一种进行理论研究和初步估算的工具来说,具有重要的意义。 (4)为了计算的便捷性,本文对水位变化过程只进行了简单的插值离散处理,随着计算机技术的发展,可以对长系列的水文数据进行函数拟合,考虑到水位变化在实际情况中还存在其他情形,需进一步研究各情况下理论解的实际应用。 (5)在河渠—半无限潜水非稳定流模型中,除河渠水位变换对附近潜水具有重要影响外,其垂向水量交换及含水层非均质特性也是重要的影响因素,笔者认为,在模型中可将垂向水量交换概化为源汇项,假设其强度为一稳定值;此外对于含水层非均质特性问题,可以先着眼于层状非均质模型的研究,受限于文章篇幅,这里不再作详细展开,但应作为后续研究的重点。3.2 求 参
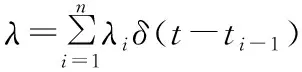
3.3 河渠与潜水之间交换量计算
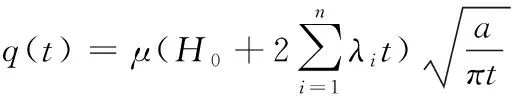
4 实 例
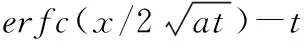


5 结 论

