基于AEO-Schumacher-Usher模型的径流及地下水位预测
胡顺强,崔东文
(1. 云南省文山州水利电力勘察设计院,云南 文山 663000;2. 云南省文山州水务局,云南 文山 663000)
1 研究背景
探索具有较好预报精度的模型及方法对于径流及地下水位预测研究具有重要意义。目前用于径流预报研究的模型有人工神经网络模型[1]、集对分析模型[2]、支持向量机模型[3]、投影寻踪回归模型[4]、小波分析模型[5]、随机森林模型[6]、组合预测模型[7]等;用于地下水位预测研究的模型有时间序列模型[8]、回归模型[9]、神经网络模型[10]、灰色马尔可夫链模型[11]、支持向量机模型[12]等。生长模型作为趋势外推法的一种重要方法,除用于描述和预测生物个体的生长发育以外,已在技术、经济特性等领域得到应用。常用的生长模型有Logistic模型、Richard模型、MMF模型、Hyperbola模型、Korf模型、Weibull模型、Gompertz模型、Usher模型、Schumacher模型等,已在人口预测、地表沉降、油气田产量预测、电能消费量预测、围岩变形预测等行业领域得到应用,但鲜见于水文预报及地下水位预测研究领域。研究表明,制约生长模型应用的关键在于模型相关参数的合理选取,目前主要采用四点法、三段法、最小二乘法等进行参数估算,不但求解复杂,且效率不高。虽然遗传算法(GA)、粒子群优化(PSO)算法、果蝇优化算法(FOA)、差分进化(DE)算法已尝试用于Weibull模型、Richards模型、Gompertz模型、Usher模型参数的选取,具有较好的实际意义,但存在以下方面的不足:①GA、PSO等传统智能算法存在收敛速度慢和易陷入局部最优值等问题,难以获得理想的优化效果;②算法验证缺失或存在不足。实践表明,对于标准测试函数具有较好优化效果的群体智能算法,其在解决实际优化问题中不一定能获得较好的应用效果;③目前仅针对Weibull模型、Gompertz模型、Richards模型、Usher模型相关参数进行单一优化,组合生长模型应用较少,没有同时针对组合生长模型参数和权重系数优化的实例。
为拓展生长模型在径流及地下水位预测中的应用范畴,提高模型预测精度,本文选取Schumacher、Usher 2种单一生长模型进行组合,提出人工生态系统优化(artificial ecosystem-based optimization,AEO)算法[32]-组合生长预测模型。本文内容结构如下:①介绍人工生态系统优化(AEO)算法,结合本文优化实例,选取6个标准测试函数在5维、10维、15维条件下和本文Schumacher、Usher模型参数优化实例对AEO算法进行仿真验证,并与鲸鱼优化算法(WOA)、灰狼优化(GWO)算法、教学优化(TLBO)算法、PSO算法的仿真结果进行比较。②利用AEO算法同时优化该组合生长模型参数和组合权重系数,提出AEO-AEO-Schumacher-Ushe预测模型及实现步骤,构建AEO-Schumacher、AEO-Usher、AEO-SVM对比预测模型。③基于两个径流及地下水位预测实例对AEO-Schumacher-Usher、AEO-Schumacher、AEO-Usher、AEO-SVM模型进行验证及对比分析,旨在检验AEO-Schumacher-Usher模型应用于径流及地下水位预测的可行性和有效性。
2 人工生态系统优化算法-组合生长预测模型
2.1 人工生态系统优化算法
人工生态系统优化(artificial ecosystem-based optimization,AEO)算法[13]是Zhao等人于2019年通过模拟地球生态系统中能量流动而提出一种新型元启发式优化算法,该算法通过生产算子、消费算法和分解算子对生态系统中的生产、消费和分解行为进行模拟来达到求解优化问题的目的。生产算子旨在加强AEO算法勘探和开发之间的平衡能力;消费算子用于改进AEO算法的探索能力;分解算子旨在提升AEO算法的开发性能。与传统群智能算法相比,AEO算法不但实现简单,除群体规模和最大迭代次数外,无需调整其他任何参数,且具有较好的寻优精度和全局搜索能力。
AEO算法遵行以下3个准则:①生态系统作为种群包括3种生物:生产者、消费者和分解者,且种群中分别只有一个个体作为生产者和分解者,其他个体作为消费者。②每个个体都具有相同的概率被选择为食肉动物,食草动物或杂食动物。③群体中每个个体的能量水平通过适应度值进行评价,适应度值按降序排序,适应度值越大表示最小化问题的能量水平越高。
参考文献[13],AEO算法数学描述简述如下:
(1)生产者。在AEO算法中,生产者(最差个体)通过搜索空间上下限和分解者(最优个体)进行更新,更新后的个体将引导种群中的其他个体搜索不同的区域。模拟生产者行为的数学模型如下:
x1(t+1)=[1-(1-t/T)r1]xn+(1-t/T)r1xrand(t)
(1)
式中:x1表示生产者个体空间位置;xn表示当前群体中最佳个体空间位置;n表示种群规模;T表示最大迭代次数;t表示当前迭代次数;xrand=r(U-L)+L,表示搜索空间中随机生成的个体空间位置,U、L为空间上下限;r1表示[0,1]之间的随机数。
(2)消费者。生产者提供食物能量后,每个消费者均可随机选择能量水平较低的消费者或生产者或两者兼有获得食物能量。
如果消费者被随机选择为草食动物,它只以生产者为食。模拟草食动物消费行为的数学模型如下:
xi(t+1)=xi(t)+C[xi(t)-x1(t)],i∈[2,…n]
(2)
如果消费者被随机选择为食肉动物,它只能随机选择能量水平较高的消费者为食。模拟食肉动物消费行为的数学模型如下:
(3)
如果消费者被随机选择为杂食动物,它可以同时选择能量水平较高的消费者和生产者为食。模拟杂食动物消费行为的数学模型如下:
(4)
式中:xi表示第i个消费者个体空间位置;C表示具有levy飞行特性的消费因子,即C=0.5v1/|v2|,其中v1~N(0,1),v2~N(0,1),N(0,1)表示呈正态分布、均值为0、标准差为1的概率密度函数;xj表示具有较高能量水平的消费者和生产者;r2表示是[0,1]范围内的随机数;randi()表示产生均匀分布的伪随机整数;其他参数意义同上。
(3)分解者。为提高算法的开发性能,AEO算法允许每个个体的下一个位置围绕最佳个体(分解者)传播,并通过调节分解因子D和权重系数e、h来更新群体中第i个消费者的空间位置。其模拟分解行为的数学模型如下:
xi(t+1)=xn(t)+D(exn(t)-hxi(t)),i∈1,…,n
(5)
式中:D表示分解因子,表达式为D=3u,u~N(0,1);e、h表示权重系数,表达式为e=r3randi([1 2])-1,h=2r3-1,其中r3表示[0,1]之间的随机数。
2.2 组合生长模型
(1)Schumacher模型。Schumacher模型是由学者Schumacher针对Richards模型缺陷而提出的一种生长模型,目前主要在植物生长拟合[14]、天然林生长预测[15]方面得到应用。Schumacher模型表述形式多样,本文利用式(6)所示的函数模型进行径流及地下水位预测。
(6)

(2)Usher模型。Usher模型最早由美国学者Usher于1980年提出用于描述增长信息随时间变化的数学模型,目前已在围岩变形预测[16]、油田开发[17]、沉降预测[18]等领域得到应用。Usher模型表述形式多样,本文利用式(7)所示的Usher函数模型进行径流及地下水位预测。
(7)

利用AEO算法对Schumacher-Usher模型参数和权重系数进行优化,得到待优化组合生长模型:
(8)

2.3 组合生长模型结构及预测实现步骤
AEO-Schumacher-Usher预测模型结构组成为:首先由Schumacher、Usher两个单一生长模型线性组合构建Schumacher-Usher组合模型,利用AEO同时优化Schumacher-Usher组合模型参数α、γ、βo、A、B、Co、D以及Schumacher权重系数ωs,建立AEO-Schumacher-Usher预测模型。
AEO-Schumacher-Usher预测实现步骤归纳如下:
(1)选取径流或地下水位预测影响因子,构造组合生长模型预测的输入、输出向量,合理划分训练样本和预测样本,利用式(9)对2个实例数据序列进行归一化处理;设定组合生长模型参数和权重系数的搜寻范围。
z′=(z-0.5zmin)/(2zmax-0.5zmin)
(9)
式中:z′表为经过归一化处理的数据;z表为原始数据;zmax和zmin分别为序列中的最大值和最小值。
(2)确定组合生长模型适应度函数。本文选用训练样本均方误差作为适应度函数,描述如下:
(10)

(3)设置AEO算法种群规模n、最大迭代次数T和算法终止条件;随机初始化生态系统xi,计算适应度值,保留当前最佳个体空间位置xbest。令当前迭代次数t=0。
(4)利用式(1)更新生产者空间位置。
(5)在[0,1]之间生成随机数r,若r<1/3,利用式(2)更新消费者个体空间位置;若1/3≤r≤2/3,利用式(3)更新消费者个体空间位置;其他利用式(4)更新消费者个体空间位置。计算每个个体空间位置适应度值,找到并保留当前最佳个体空间位置xbest。
(6)利用式(5)更新分解过程中消费者个体空间位置,计算每个个体适应度值,找到并保留当前最佳个体空间位置xbest。
(7)比较并保存最佳个体空间位置,即算法最优解xbest。
(8)令t=t+1。判断算法是否达到终止条件,若是,输出全局最优解xbest,算法结束;否则重复步骤(4)~(8)。
(9)输出最优适应度值及全局最优位置xbest,xbest即为组合生长模型参数和权重系数向量。将参数xbest代入组合生长模型进行预测。
3 实例应用
3.1 数据来源及分析
实例1数据资料来源于文献[19]某水库年径流预测。该水库年均径流量受到流域内年降水量、年森林采伐面积、年采伐量和年均含沙量等因子的影响,见表1。为便于与文献[20]GA-BP、文献[21]IEA-EPP模型预测结果作对比,本文选取森林采伐面积(m2)、采伐量(m3)、年均降水量(mm)、年均含沙量(kg/m3)作为模型输入,年均流量(m3/s)作为输出,并以 1983-1998年的数据作为训练样本,1999-2003年数据作为预测样本对各模型预测性能进行验证。
实例2数据资料来源于文献[22]吉林省白城市白城46号地下水观测井1982-2004 年共 23 年实测系列资料,见表2。观测井所处白城市南部是吉林省西部干旱和半干旱平原区最具代表性的地段,经分析,该观测井 10 月平均水位、汛期6-9 月降水量、枯季 11-次年 3 月降水量与次年 5 月平均水位相关关系较好。为便以与文献[22]BP、文献[21] FSOA-PPR模型预测结果作对比,本文选取10月平均水位(m)、汛期降水量(mm)和枯期降水量(mm)作为模型输入,次年 5 月平均水位作为输出,并以1982-2000 年的数据作为训练样本,2001-2004年数据作为预测样本对各模型预测性能进行验证。
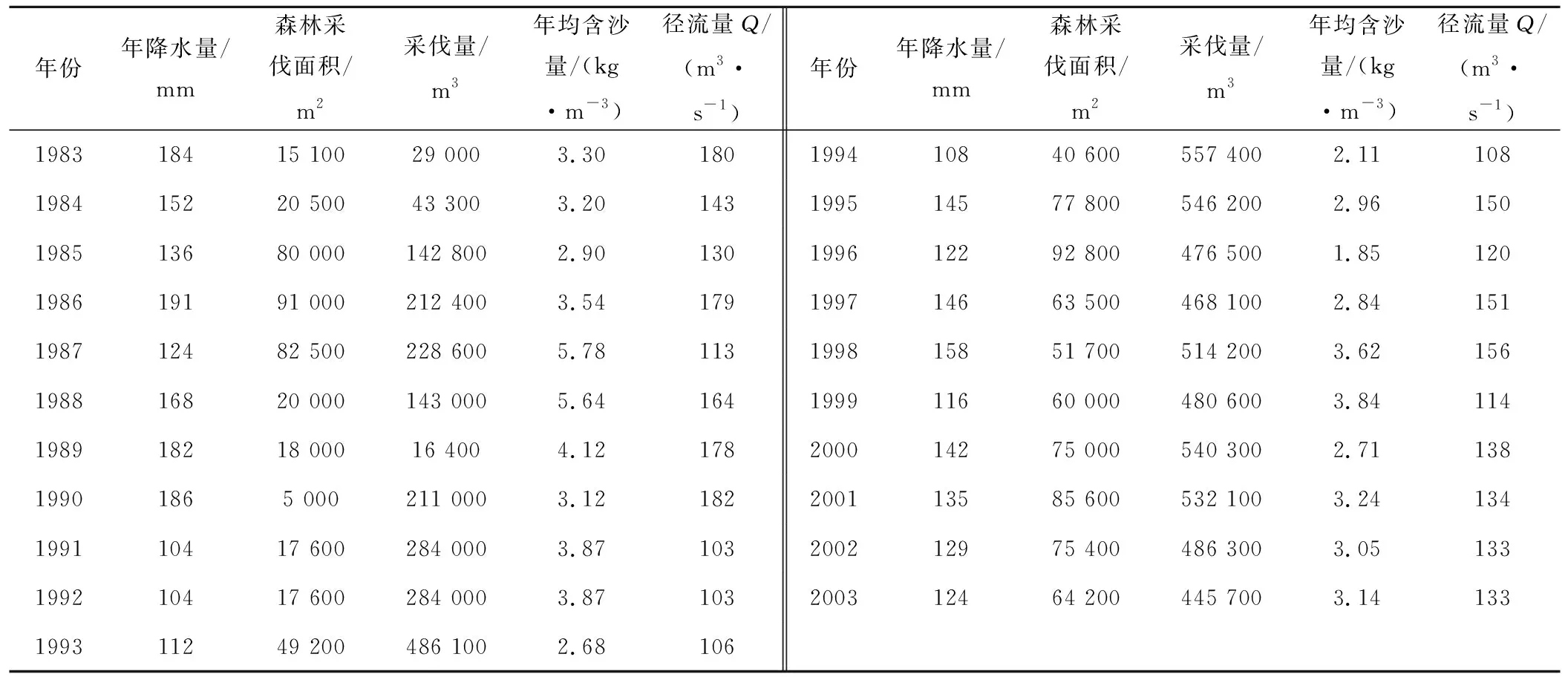
表1 某水库1983-2003 年相关因子动态变化

表2 某水库1983-2003 年相关因子动态变化
3.2 算法验证
3.2.1 标准测试函数仿真验证
结合本文实例优化维度,选取Sphere、Schwefel 1.2、Rosenbrock、Griewank、Rastrigin、Ackley 6个标准测试函数在5维、10维、15维条件下对AEO算法进行仿真验证,并与WOA、GWO、TLBO、PSO算法的仿真结果进行比较。上述6个函数变量取值范围分别为[-100,100]、[-100,100]、[-10,10]、[-600,600]、[-5.12,5.12]、[-32,32],理论最优解值均为0。其中,函数Sphere、Schwefel 1.2、Rosenbrock为单峰函数,主要用于测试算法的寻优精度;函数Griewank、Rastrigin、Ackley为多峰函数,主要用于测试算法的全局搜索能力。基于Matlab 2018a M语言实现5种算法对6个典型测试函数的20次寻优,利用平均值对5种算法寻优性能进行评估,见表3。实验参数设置如下:AEO、WOA、GWO、TLBO、PSO 5种算法最大迭代次数T=1 000,种群规模n=50。其中,WOA对数螺旋形状常数b=2;TLBO算法参数TF为1~10之间随机整数;PSO算法惯性权重wmax、wmin分别取值0.9和0.6,自我学习因c1、社会学习因子c2均取值2.0。其他参数采用各算法默认值。
(1)对于单峰函数Sphere,AEO算法在不同维度条件下20次寻优均获得理论最优值0,寻优精度优于WOA、TLBO、GWO算法,远优于PSO算法;对于倒锥形非线性函数Schwefel 2.21,AEO算法在不同维度条件下20次寻优均获得理论最优值0,寻优精度优于TLBO、GWO算法,远优于WOA、PSO算法;对于极难极小化的多维病态二次函数Rosenbrock,AEO算法在不同维度条件下的寻优精度均优于其他4种算法。

表3 函数优化对比结果
(2)对于典型多峰多模态函数Griewank,AEO算法在不同维度条件下20次寻优均获得了理论最优值0,寻优精度远优于WOA、TLBO、GWO和PSO算法;对于典型易陷入局部极值多峰函数Rastrigin,AEO、GWO算法20次寻优获得理论最优值0,寻优精度优于10维、15维条件下的WOA和TLBO算法,远优于不同维条件下的PSO算法;对于连续旋转不可分多峰函数Ackley,AEO算法在不同维度条件下20次寻优均获得相对理论最优值8.88×10-16,寻优精度优于WOA、TLBO、GWO算法,远优于PSO算法。
可见,AEO算法在5维、10维、15维条件下对上述6个测试函数均获得较好的寻优效果,寻优精度优于WOA、TLBO、GWO算法,远优于PSO算法,具有较好的寻优精度和全局搜索能力。对于上述6个测试函数,5种算法综合优化性能由优至劣依次是:AEO、TLBO、GWO、WOA、PSO算法。
3.2.2 实例问题优化
实践表明,对于标准测试函数具有较好优化效果的群体智能算法,其在解决实际优化问题中不一定能获得较好的应用效果。为验证AEO、WOA、GWO、TLBO、PSO算法在解决实际优化问题的优化性能,本文利用此5种算法对实例1、实例2进行优化,即在搜索空间搜寻一组参数,使得式(6)(Schumacher模型)、式(7)(Usher模型)的实测值与拟合值均方误差最小。并利用最优值、最劣值、平均值和标准差对AEO、WOA、GWO、TLBO、PSO算法寻优性能进行评估,见表4。5种算法参数设置同上,搜索空间均为[0,10]。

表4 实例优化对比结果
对于实例1和实例2,AEO算法对Schumacher模型、Usher模型20次寻优获得的最优值、最劣值、平均值和标准差均优于WOA、TLBO、GWO、PSO算法(除TLBO算法对Usher模型寻优获得的最优值外),标准差≤1.54×10-5,具有较好的寻优精度、全局搜索能力和稳健性能,在实际问题优化应用中表现良好。相对而言,在上述标准测试函数优化中表现较好的WOA、GWO算法,其对实例1和实例2的优化效果甚至不如PSO算法。对于实例1和实例2,5种算法综合优化性能由优至劣依次是:AEO、TLBO、PSO、GWO、WOA。
3.3 预测及分析
(1)参数设置。设置组合生长模型参数的搜索范围∈[0,10],Schumacher模型权重系数搜索范围∈[0,1];Schumacher、Usher单一生长模型参数的搜索范围∈[0,10];SVM模型惩罚因子C、核函数参数g、不敏感系数e搜索范围均为[2-5,25],交叉验证折数为3,原始数据采用[0.1,0.9]进行归一化处理。
(2)模型构建及预测。构建AEO-Schumacher-Usher、AEO-Schumacher、AEO-Usher、AEO-SVM模型对实例径流及地下水位进行训练及预测。选取平均相对误差绝对值MRE(%)、平均绝对误差MAE、决定系数R2作为评价指标,利用此4种模型对实例1和实例2进行预测,并与文献[20-22]预测结果作对比,结果见表5、表6,并给出实例1和实例2的训练-预测相对误差效果图,见图1、图2。
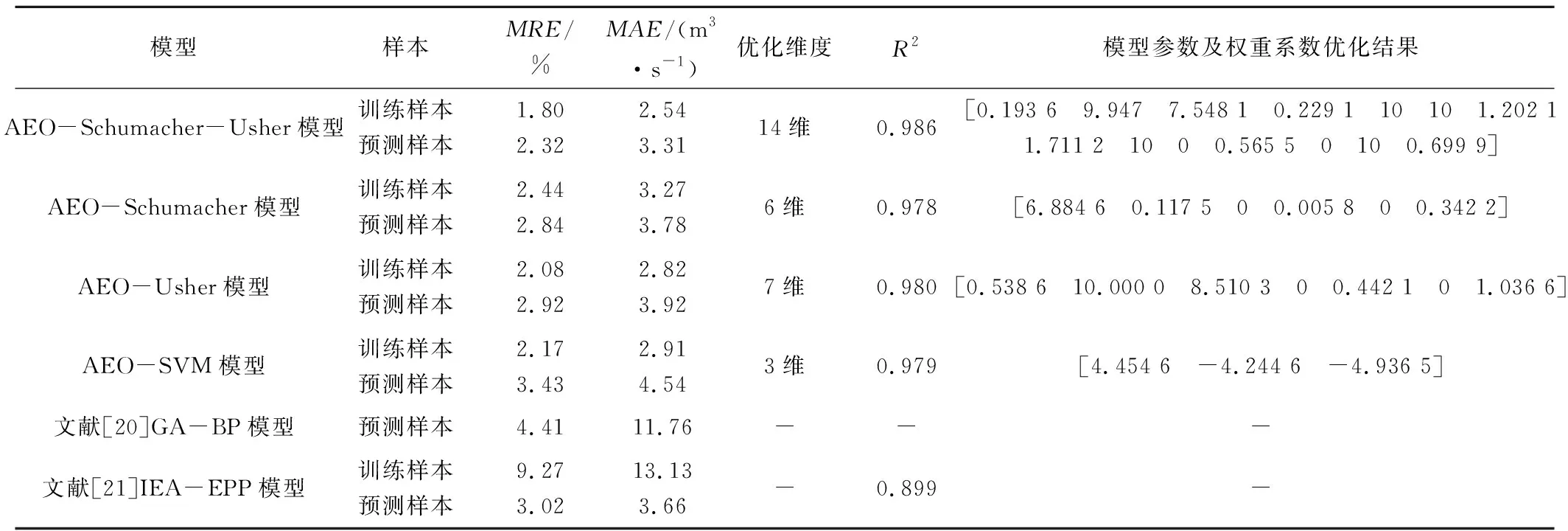
表5 实例1水库年径流量预测结果及其对比表

表6 实例2白城市46号井地下水位预测结果及其对比表

图1 实例1拟合-预测相对误差图

图2 实例2拟合-预测相对误差图
依据表5、表6及图1~图2可以得出以下结论。
(1)AEO-Schumacher-Usher模型对实例1训练样本拟合的MRE、MAE分别为1.80%、2.54 m3/s,对预测样本预测的MRE、MAE分别为2.32%、3.31 m3/s,整体决定系数R2为0.986,拟合精度、预测精度及模型决定系数R2均优于AEO-Schumacher、AEO-Usher、AEO-SVM模型及文献GA-BP、IEA-EPP模型,具有较好的预测精度和泛化能力。从单一模型来看,AEO-Schumacher、AEO-Usher模型预测精度在伯仲之间,但优于AEO-SVM模型及文献GA-BP、IEA-EPP模型。从表5及图1来看,文献IEA-EPP模型表现出欠拟合特征,即预测精度尚可,但拟合精度较差。
(2)AEO-Schumacher-Usher模型对实例2训练样本拟合的MRE、MAE分别为3.54%、0.127 m,对预测样本预测的MRE、MAE分别为0.15%、0.011 m,整体决定系数R2为0.991,拟合精度、预测精度及模型决定系数R2均优于AEO-Schumacher、AEO-Usher、AEO-SVM模型及文献BP、FSOA-PPR、FSOA-BP模型,具有较好的预测精度和泛化能力。从单一模型来看,AEO-Schumacher、AEO-Usher模型拟合、预测精度相当,精度优于AEO-SVM模型及文献FSOA-BP模型。虽然文献FSOA-PPR模型预测精度高于其他单一模型,但拟合精度劣于其他单一模型,模型精度(决定系数R2)劣于AEO-Schumacher、AEO-Usher模型。
(3)从两个实例应用效果来看,AEO-Schumacher-Usher模型具有较好的预测精度和泛化能力,表明Schumacher、Usher模型具有互补性(尤其对于实例2),AEO算法能同时有效优化组合生长模型参数和权重系数,AEO-组合生长模型用于径流及地下水位预测是可行和有效的,模型及方法可为相关预测研究提供新的途径和方法。两个实例的拟合、预测中,单一模型AEO-Schumacher、AEO-Usher模型同样具有较好的应用效果,其精度要高于AEO-SVM模型,可见单一生长模型AEO-Schumacher、AEO-Usher在径流及地下水位预测中同样具有较好的预测精度,关键之处在于合理选取模型的相关参数。
(4)从AEO-Schumacher-Usher模型的权重系数优化结果来看,对于实例1,Schumacher模型权重系数为0.699 9,大于0.5,表明Schumacher模型占主导地位;对于实例2,Usher模型权重系数0.6098,大于0.5,表明Usher模型占主导地位。AEO-Schumacher-Usher模型的预测结果不是AEO-Schumacher、AEO-Usher模型预测结果的简单加权。
(5)本实例虽然采用AEO算法对SVM模型关键参数进行优化,具有一定的智能化水平,但SVM模型的交叉验证折数V需人为设定,V值过大或过小均会导致模型出现“过拟合”或“欠拟合”现象,从而影响AEO-SVM模型的预测效果。本文提出的AEO-Schumacher-Usher组合生长模型所有参数和权重系数均由AEO算法优化获得,无需人为设定,具有较高的智能化水平和较好的实际应用价值。
4 结 论
(1)介绍人工生态系统优化(AEO)算法,针对当前算法验证中的不足,选取6个标准测试函数在5维、10维、15维条件下和本文Schumacher、Usher模型参数优化实例对AEO算法进行仿真验证,并与WOA、GWO、TLBO、PSO算法的仿真结果进行比较。结果显示:AEO算法寻优精度优于WOA、GWO、TLBO、PSO算法,具有较好的寻优精度、全局搜索能力和算法稳健性能。
(2)基于Schumacher、Usher单一生长函数模型构建Schumacher-Usher组合生长模型,针对组合生长模型参数及权重系数选取困难的实际问题,利用AEO算法同时优化组合生长模型参数和权重系数,提出AEO-Schumacher-Usher组合预测模型和优化方法,并构建AEO-Schumacher、AEO-Usher、AEO-SVM作对比验证模型,并以两个年径流预测和地下水位预测为例进行验证。验证表明,AEO-Schumacher-Usher模型拟合及预测精度均优于AEO-Schumacher、AEO-Usher、AEO-SVM模型和相关文献模型,Schumacher、Usher模型具有互补性,AEO算法能同时有效优化组合生长模型参数和权重系数,AEO-Schumacher-Usher组合生长模型用于径流及地下水位预测是可行和有效的,模型具有较好的预测精度和泛化能力,模型及方法可为相关预测研究提供新的途径和方法。

