C++中的浮点数在机器中的存储精度问题

智爱娟 刘雅琴 侯凤云

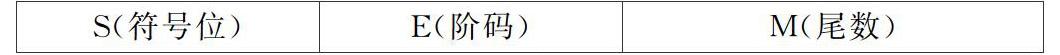
摘 要： 浮点数是C++中最基本的数据类型，本文讨论了浮点数在机器内存中的存储情况、浮点数的显示以及C++语言编程中使用浮点数需要注意的几个问题。

关键词： C++;浮点数;存储;显示;精度

【中图分类号】TP31     【文献标识码】A     【DOI】10.12215/j.issn.1674-3733.2020.37.135

1 引言

C++語言中的浮点数有float、double和long double三种类型，在使用C++语言编写程序的过程中，使用最多的是float和double类型的浮点数。本文以float和double类型的浮点数为例，说明浮点数在机器内存中的存储精度以及在C++语言编程中使用浮点数时需要注意的几个问题。

2 浮点数在机器内存中的存储

C++语言中的float和double类型的浮点数在机器内存中存储时分别按照IEEE754标准中的单精度浮点格式和双精度浮点格式进行的，而long double类型的浮点数在机器中存储时的格式和长度则与机器所采用的微处理器类型有关。比如，在IA-32和X86-64系统中long double是按照IEEE754标准中的80位扩展双精度格式进行存储的。

IEEE754标准规定，单精度浮点数在机器中采用32位二进制表示，其中1位符号位，8位阶码，23位尾数，阶码采用移码表示（偏置常数位127），尾数采用原码表示（规格化形式，数值最高位的“1”隐含，不表示）;双精度浮点数在机器中采用64位表示，其中1位符号位，11位阶码，52位尾数，阶码采用移码表示（偏置常数位1023），尾数采用原码表示（规格化形式，数值最高位的“1”隐含，不表示）。

任意浮点数N均可表示成规格化形式为：±1.M×2e，对应IEEE754格式如下（小数点前总是“1”，故可隐含表示）：

如果浮点数N为正数，则符号位S为0;N为负数，则符号位S=1。单精度浮点格式中，阶码E=e+127;双精度浮点格式中，阶码E=e+1023。

例如，将十进制数1234567890分别赋值给float型变量a和double型变量b，变量a和b的机器数分别是多少呢？

十进制数1234567890转换为二进制为：10010011001

01100000001011010010B=1.0010011001011000000010110

10010*230

因为是正数，S=0;指数e=30。

对于变量a，阶码E=e+127=30+127=157=10011101B;M取小数点后23位，第24位采用“0舍1入”进行舍入处理，M=001 0011 0010 1100 0000 0110。变量a的机器数是：0100 1110 1001 0011 0010 1100 0000 0110，用十六进制表示为：4E932C06。

对于变量b，阶码E=e+1023=30+1023=1053=10000011101B;M取52位，M=0010 0110 0101 1000 0000 1010 0000 0000 0000 0000 0000 0000 0000。变量b的机器数是：0100 0001 1101 0010 0110 0101 1000 0000 1010 0000 0000 0000 0000 0000 0000 0000，用十六进制表示为：41D26580A0000000。

3 浮点数的显示

由于IEEE754单精度浮点数的尾数M为23位二进制表示，双精度浮点数的尾数为52位二进制表示，再加上1位隐含位“1”，因此单精度浮点数的都有效二进制位为24位，双精度为53位。而107<224<108，1017<253<1018，故float型浮点数在机器上显示时最多可显示8位有效数字，其中7位为精确值，double型浮点数则能显示18位有效数字，其中17位为精确值。IEEE754浮点数可以用下式转换为二进制数：（-1）S*1.M*2e。

例如，将变量a的机器数4E932C06H转换为二进制为：（-1）0*1.001 0011 0010 1100 0000 0110*230=1001001100

101100000001100000000，即十进制的1234567936，这个值比实际值大46。但是，采用同样的方法将变量b的机器数41D26580A0000000H转换为十进制为1234567890，结果和实际值相同。由此可见，double型浮点数的精度比float型浮点数的精度高。

4 在C++语言中使用浮点数应该注意的几个问题

（1）设计浮点数类型的目的是为了实现工程计算和科学计算，在工程计算和科学计算中往往没有完全精确的计算结果，需要的是近似值。因此，在要求精确计算结果的场合（尤其是应用程序中），比如，对货币计算时一般不要使用浮点型数据，否则，将会得到错误的结果。

例如：假设想用十元钱去买价格不等的游戏币，游戏币的标价分别是1元、2元、3元，一直到10元不等。购买时，打算从标价为1元游戏币开始按照价格从低到高的顺序依次购买，每种购买一个，直到所剩的钱不够支付任何一种游戏币为止，最后，共可以购买多少个游戏币呢？还会剩余多少零钱呢？

采用浮点数表示钱数和游戏币的价格，用C++语言编写程序如下：

#include

#include

using namespace std;

int main（ ）

{

int itemsBought = 0;//购买游戏币个数

double Price;//游戏币价格

double Funds = 10.00;//总钱数

for （Price =1.00; Funds >= Price; Price +=10.00）

{

Funds -= Price;

itemsBought++;

}

cout<     cout<<"剩余钱数： "<     }

编译运行程序，得到结果为：“3个游戏币”，“剩余钱数：4.00元”。很明显，程序运行得到的结果是错误的。

解决这个问题的正确办法是：在编写C++程序时，浮点数表示钱数和游戏币的价格。

使用int类型代替double类型修改上面的程序如下：

#include

using namespace std;

int main（ ）

{

int itemsBought = 0;//购买游戏币个数

int Price;//游戏币价格

int Funds = 100;//总钱数

for （Price = 10; Funds >= Price; Price += 10）

{

Funds -= Price;

itemsBought++;

}

cout<     cout<<"剩余钱数："<     }

重新编译运行程序，输出结果：“4个游戏币”和“剩余钱数：0元”。显然，程序执行结果正确。

（2）在程序中不要用浮点型数据作为循环变量

例如，编写程序：从0开始按照逐次递增0.2输出一直到10。在程序中用float型作为循环变量，用C++编程如下：

#include

using namespace std;

main（int argc，char *argv）

{

float i;

for（i=0;i<10;i+=.2）

printf（"%10f"，i）;

return 0;

}

編译运行程序，得到的输出结果如下：

显然，程序输出结果是错误的。

解决问题的方法是：先将数据起始值、终止值和递增量都扩大10倍变成整数，输出前将结果再缩小10倍。重新编写程序如下：

#include

using namespace std;

main（int argc，char *argv）

{

int i，a，b;

for（i=0;i<=50;i=i+2）

{

a=i/10;

b=i%10;

cout<     }

return 0;

}

重新编译运行程序，结果如下：

显然，程序输出是正确的。

（3）不要在程序中判断浮点数是否相等

例如，判断数据99.6345489和99.6345481的大小，编程如下：

#include

using namespace std;

int main（void）

{

float m = 99.6345489;

float n = 99.6345481;

if（m     cout<<"m     else if（m==n）

cout<<"m==n"<     else

cout<<"m>n"<     return 0;

}

阅读分析上述程序，程序结果应该“m>n”，但是程序执行结果却是“m ==n”。结果出错的原因就是浮点数无法表示非常精确的结果。如程序中的float型变量m和n只能有8位有效数字，是无法区分出末位的9和1。在内存中，m和n的二进制数都是0x419F0329。

5 结束语

本文对C++程序中浮点数的使用作了简单探讨，为了编写出安全、有效的代码，建议在用高级语言编写实际应用项目程序时尽量避免使用浮点型数据。

参考文献

[1] 丁展.C/C++程序设计[M].北京：电子工业出版社，2018.

[2] 比雅尼.C++程序设计语言[M].北京：机械工业出版社，2002.

[3] 袁春风.计算机系统基础[M].北京：机械工业出版社，2014.

[4] 唐朔飞.计算机组成原理[M].北京：高等教育出版社，2008.

[5] 李继灿.新编16/32位微型计算机原理及应用.北京：清华大学出版社，2018.