基于局部加权长短时记忆网络的无人机DOA估计算法

郭业才， 施钰鲲

（1.南京信息工程大学电子与信息工程学院，南京210044；2.江苏省大气环境与装备技术协同创新中心，南京210044；3.南京信息工程大学滨江学院，江苏无锡214105）

0 引 言

随着无人机使用的普及率迅速提升，人们对无人机安全问题也十分关注。为提高无人机使用的安全性，开发一套高精度无人机定位系统十分必要。在无人机定位技术中，波达方位（Direction of Arrival，DOA）估计技术受到研究者的关注［1-2］。传统的DOA估计算法，如基于高分辨率技术的多重信号分类（Multiple Signal Classification，MUSIC）算法［3］和旋转不变性子空间（Estimating Signal Parameter Via Rotational Invariance Techniques，ESPRIT）［4］算法计算量大、实时性差。近年来，基于机器学习的DOA 估计算法开始出现，文献［5］中给出了从广义互相关（Generalized Cross Correlation，GCC）向量中提取方位特征送入多层感知机（Multilayer Perceptron，MLP）网络学习的DOA 估计算法，抗噪性较差。文献［6］中提出了基于模拟退火思想（Simulated Annealing，SA）的改进粒子群优化算法（Particle Swarm Optimization，PSO）和误差反向传播（Back Propagation，BP）网络的DOA 估计算法，有效地解决了BP网络易陷入局部极小点问题，但低信噪比时估计精度不高。文献［7］中提出了基于卷积神经网络（Convolutional Neural Networks，CNN）的DOA 估计算法，虽精度较高，但卷积计算量较大。文献［8-9］中通过切换波束天线阵获得无人机功率信号并进行DOA估计，仍存在天线实际辐射方向对算法的影响。

为解决现有DOA估计算法稳定性差、定位精度较低、泛化性弱等问题，提出了基于局部加权长短时记忆（Local Weighted Long Short Term Memory，LWLSTM）网络的无人机DOA估计算法，该算法利用圆阵天线对无人机的正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）信号功率进行实值化和特征提取，选取第n个阵元平均接收信号功率与所有阵元平均功率值总和之比作为网络输入，通过LWLSTM网络将方位角θ恢复，实现无人机DOA估计。

1 DOA估计模型

1.1 阵列信号模型

接收信号天线阵为N 个相同全向阵元组成的均匀圆阵，如图1 所示。

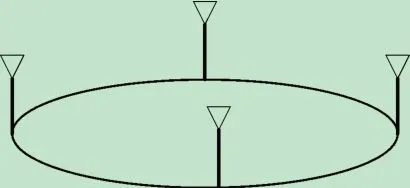
图1 N天线均匀圆阵

假设无人机信号s（k）以方位角θ∈［0，2π）被第n个阵元接收，即

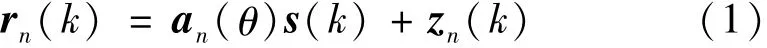
式中：an（θ）为方位角为θ 的第n 个阵元响应矢量；zn（k）为圆对称、独立相同分布、均值为0、方差为σ2的加性高斯白噪声，n∈｛1，…，N｝，k∈｛1，…，K｝，且

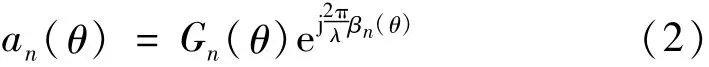
式中：Gn（θ）为方位角为θ 的实数阵元增益；βn（θ）为信号到达第n个阵元的时延［10］。

1.2 基于切换天线功率的DOA估计算法

在平稳条件下，相同时间内，第n 阵元接收K 个样本的平均功率为

式中：PA为信号平均功率。由G2n（θ）的变化，可推断Pr，n与θ间有潜在的关系，定义rn，R（k）= Re［rn（k）］，rn，I（k）= lm［rn（k）］，下标R 为实部，I 为虚部。则rn（k）的平方和为

因此，通过最大似然估计可从测量的信号功率中恢复方位角θ［12］。

2 局部加权LSTM网络框架

设xn为第n个阵元接收信号功率与所有阵元接收信号功率的和的比值，即

本文将无人机DOA估计视作分类问题，通过建立方位角θ和LWLSTM 网络学习特征的非线性映射关系，将xn作为局部加权长短时记忆（LWLSTM）网络的输入，对其进行分类，根据分类结果选取对应角度子区间，从而将θ从xn中恢复。

2.1 LSTM网络

长短时记忆（Long Short Term Memory，LSTM）［13］模型网络结构，如图2 所示。

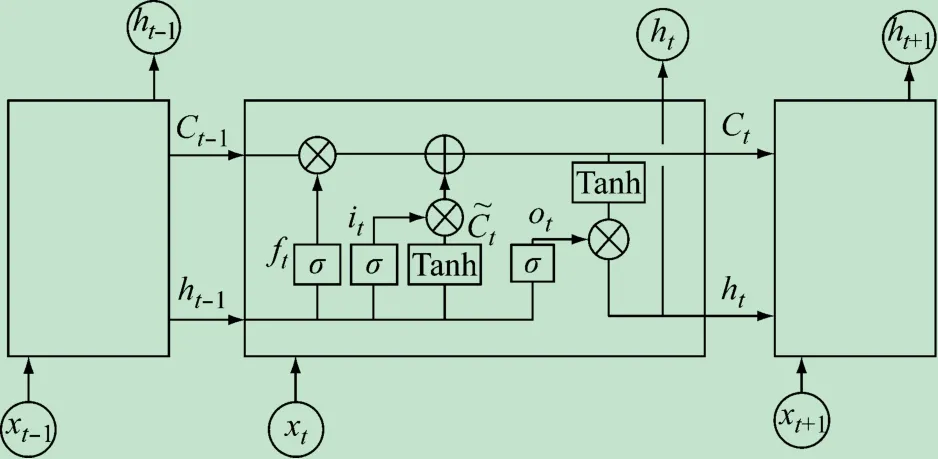
图2 LSTM结构示意图

LSTM模型关系式为

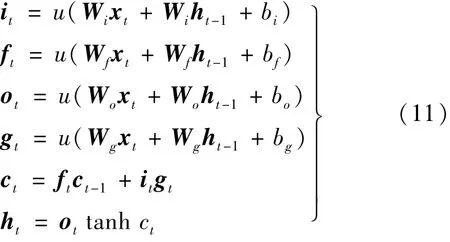
式中：xt、ht和ct分别为t 时刻的输入、输出和记忆状态；ht-1和ct-1分别为前一时刻的输出和记忆状态；（Wi，bi）、（Wf，bf）、（Wo，bo）、（Wg，bg）分别为输入门it、遗忘门ft、输出门ot和候选单元值gt的权矩阵和偏置矩阵；u（·）为sigmoid 激活函数，tanh（·）为双曲正切激活函数。

2.2 LWLSTM网络

为解决小样本时，LSTM 网络存在欠拟合问题，引入核函数对LSTM网络的损失函数和反向传播权矩阵Wf、Wi、Wo和Wc偏导进行局部加权，对误差进行非线性映射，赋予不同样本不同权重，避免欠拟合现象、提高网络泛化性能。即

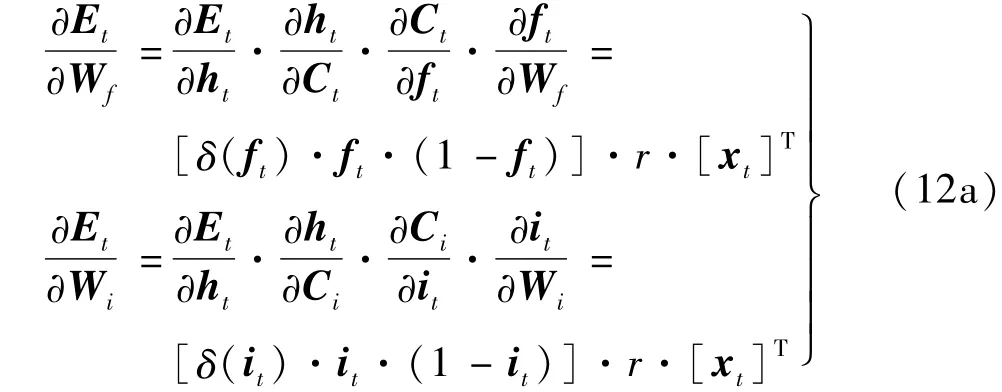
式中：e为核函数通过误差赋予不同样本的权重，使预测值ht更接近标签yt。为选择最合适的核函数，对不同的核函数进行了10 次仿真，结果见表1。

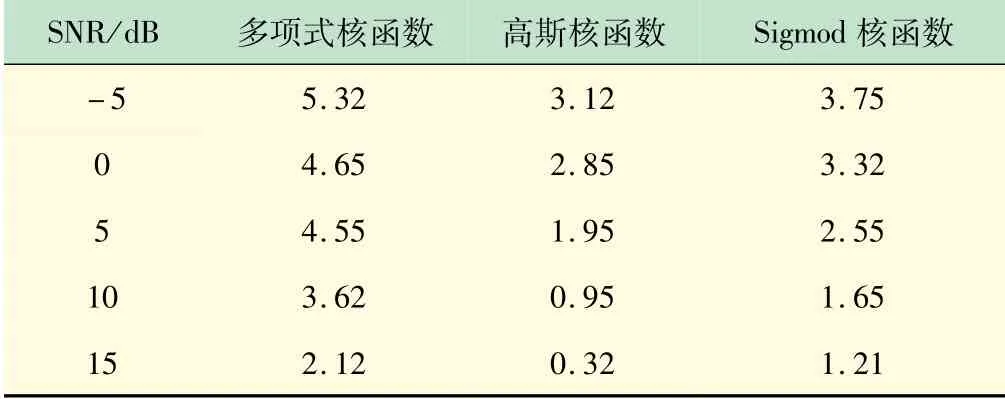
表1 基于不同核函数的LWLSTM神经网络DOA估计均方根误差

表1 表明，局部加权的回归核函数为高斯核函数时估计精度最高，e为

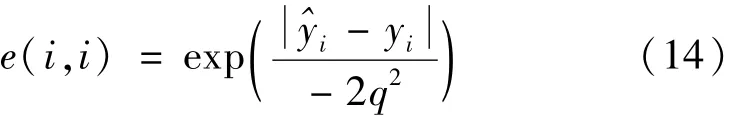
式中：^yi为输出；yi为标签；q 为控制核函数径向作用的宽度参数，影响样本权重。选择最合适的q值，对不同q值进行了10 次仿真，得到的结果如表2 所示。

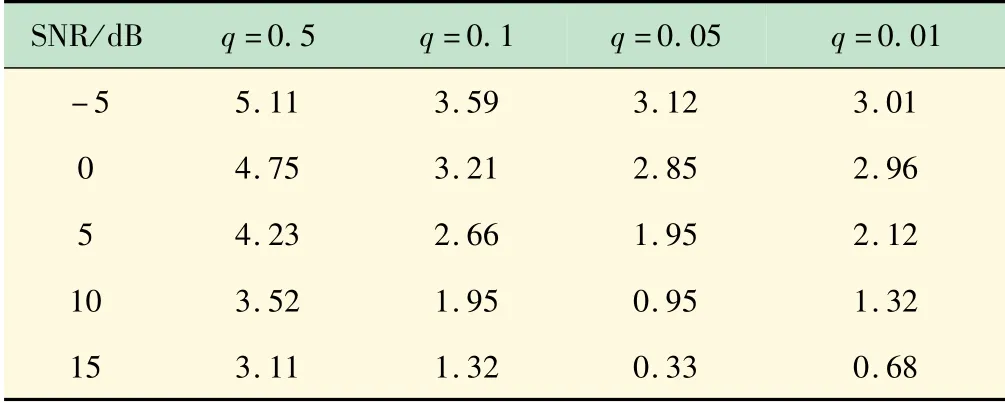
表2 基于不同q值的LWLSTM神经网络DOA估计均方根误差

表2 表明，q = 0.05 时，DOA估计精度最高，因此q值选取为0.05。

2.3 性能评价指标

本文采用均方根误差（Root Mean Square，RMSE）来比较基于LWLSTM、MLP、模拟退火粒子群优化和反向传播（Simulated Annealing Particle Swarm Optimization-Back Propagation，SAPSO-BP）SAPSO 和CNN的DOA估计方法的稳定性和精确性。RMSE 定义为

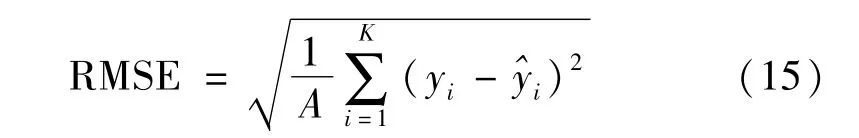
式中：A为数据集样本个数；yi与^yi分别表示真实值与估计值。

3 算法仿真

3.1 仿真条件

仿真环境为开放圆形区域，N 个天线组成均匀圆阵［14］，以圆阵圆心为坐标原点，将区域均匀分为M 个扇形范围，取N = 8，M = 36，8 个天线成十字圆阵。信号源为无人机发送的OFDM信号，快拍数为200，信噪比为10 dB。数据集为无人机从0° ～360°每10°范围内产生500 个OFDM信号样本，共18 000 个样本。按8∶2的比例随机抽取训练集和测试集［15-16］。实验样本为操场上固定圆心，从0° ～360°每10°范围内收集10个定点的无人机OFDM信号，共360 个，如图3 所示。实验中所使用的无人机，如图4 所示。

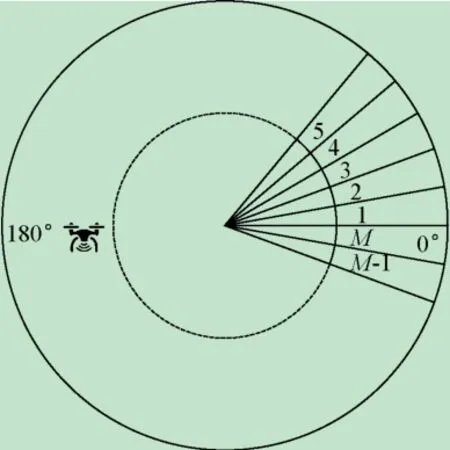
图3 仿真环境示意图

图4 无人机实物图

3.2 无人机DOA估计精确性比较

通过混淆矩阵比较DOA估计算法的精确性，矩阵中数字为多分类模型的百分比准确率。因分类区间太多，只统计350° ～90°之间11 个角度，纵坐标为标签角度θ，横坐标为当前角度φ 的分类结果。图5 ～8 表明，本文算法的精确性明显高于基于MLP 和SPASOBP的DOA估计算法，略高于基于CNN 的DOA 估计算法。

3.3 信噪比对算法性能的影响

信噪比对算法性能的影响，如图9 所示。随着信噪比的增大，基于LWLSTM、SAPSO-BP、MLP 和CNN的DOA估计算法的RMSE都逐渐减小，但由于实验环境存在电磁和机械噪声干扰，使得实验测得的均方根误差大于仿真测得的结果。尽管如此，本文算法的RMSE均小于其他算法，且与仿真结果一致。

图5 LWLSTM的混淆矩阵

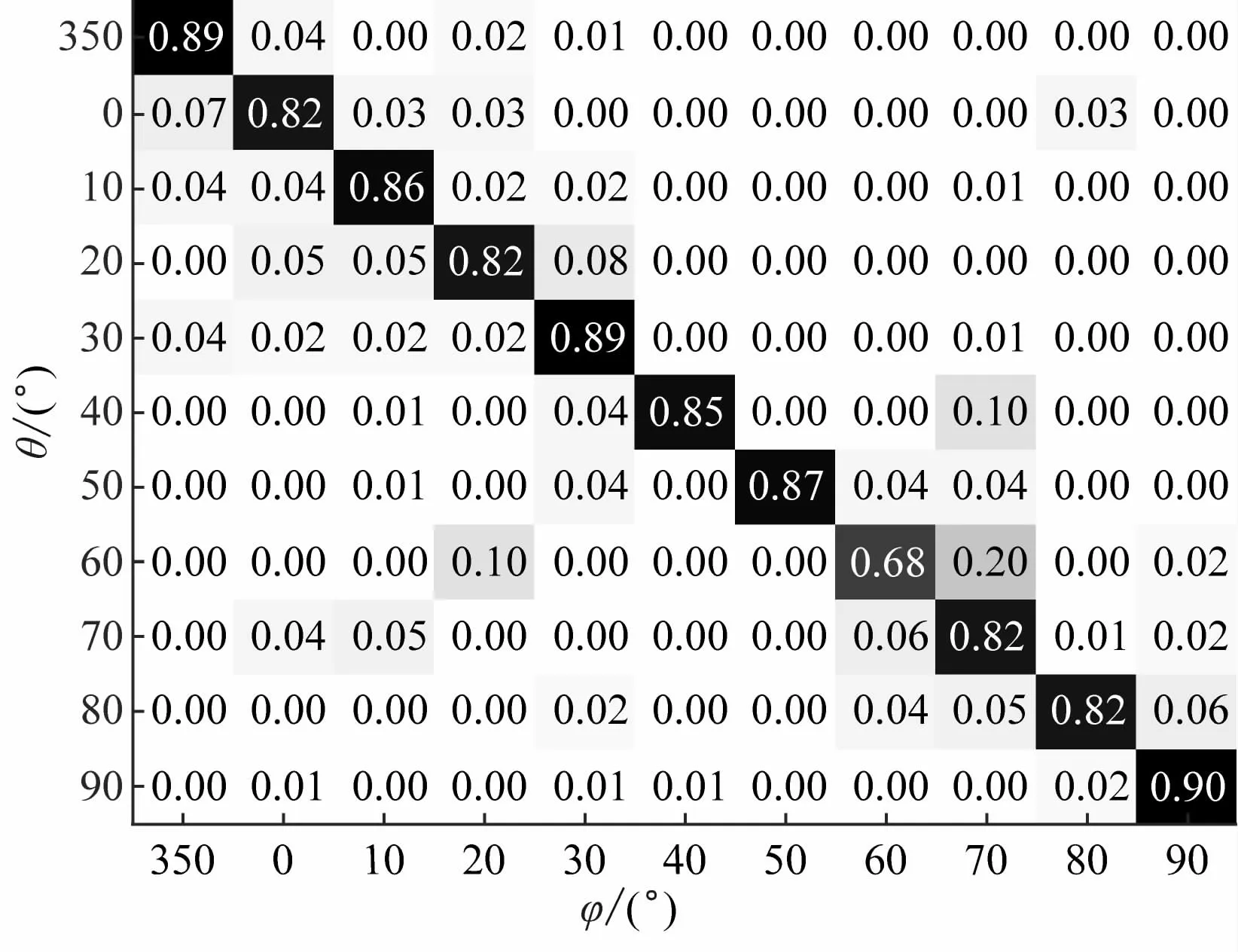
图6 MLP的混淆矩阵

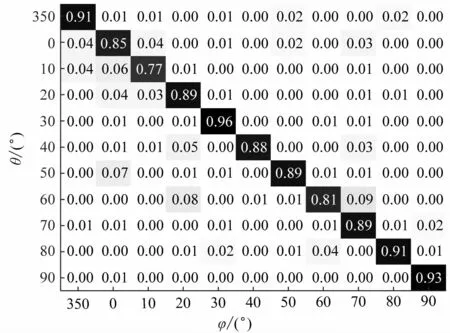
图7 SPASO-BP的混淆矩阵

3.4 阵元个数对算法性能的影响

阵元数对算法性能的影响，如图10 所示。图10表明，实验测得的均方根误差（RMSE）均大于仿真测量值，但随着阵元数和网络提取的特征数增加，几种算法的RMSE都逐渐降低且变化趋于平缓，而本文算法的RMSE比其他算法的都小，实验测量结果与仿真结果一致。

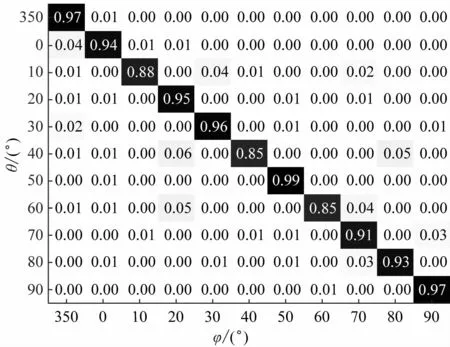
图8 CNN的混淆矩阵

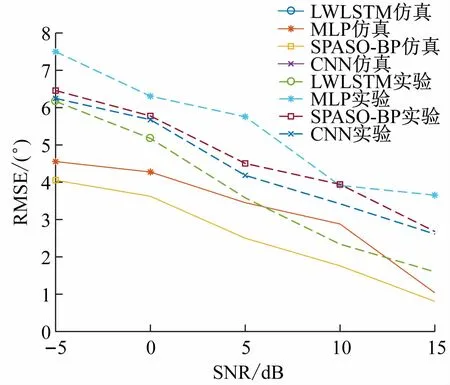
图9 信噪比对算法性能的影响

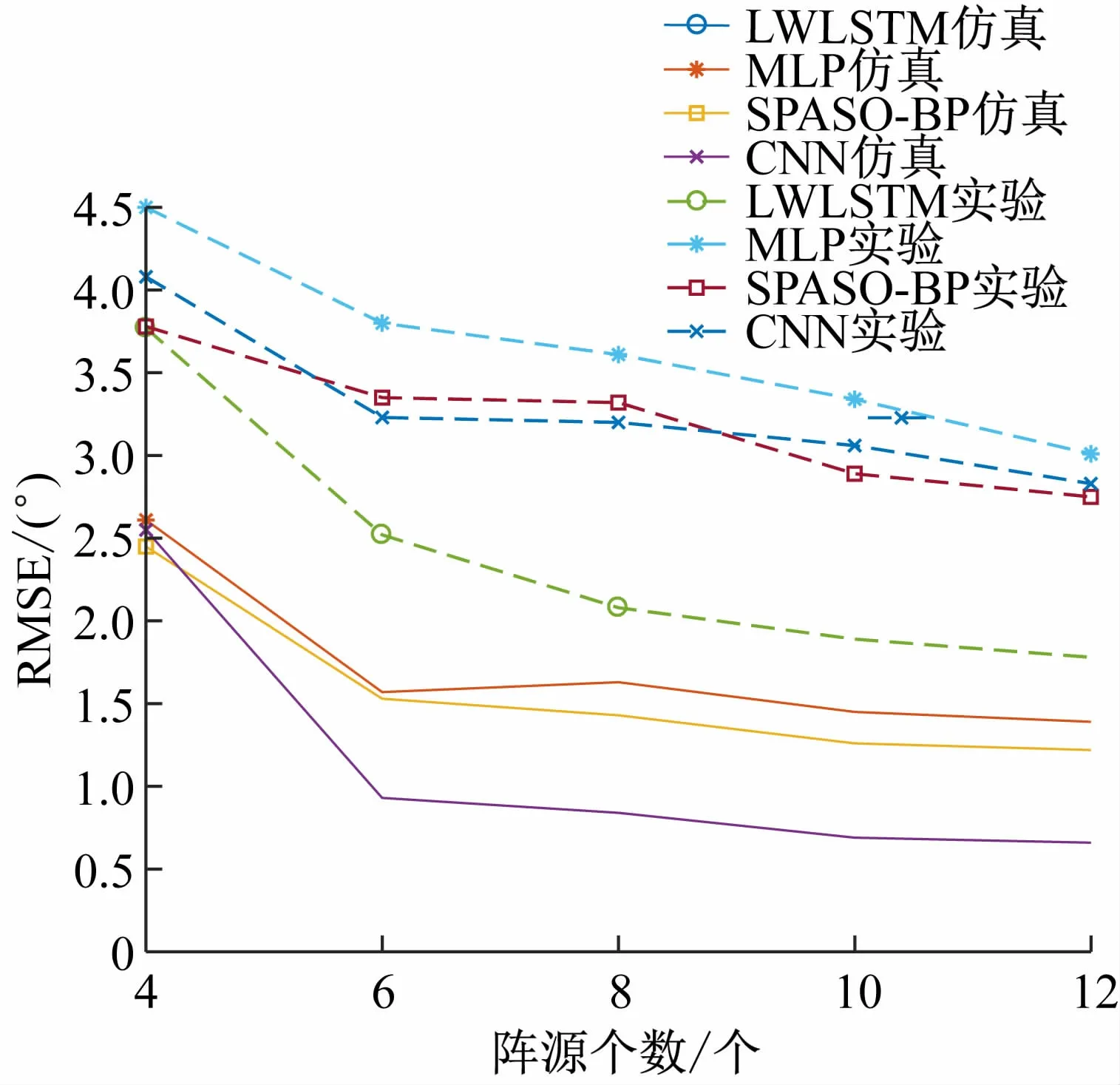
图10 阵元数对算法性能的影响

4 结 语

本文通过圆阵天线接收无人机OFDM 信号，将单阵元接收信号功率与所有阵元接收功率之和的比值作为网络输入，对LSTM进行局部加权回归，最后得到基于LWLSTM网络的无人机DOA 估计算法。仿真与实验结果表明，与基于SAPSO-BP、MLP 和CNN 的DOA估计算法相比，该算法具有更好的抗噪能力、准确性和泛化性。