基于秩和比评价模型的最优方案选择

（西华大学，四川 成都 610039）

现如今科技生活等快速发展，为我们带来了很大的便利，但层出不穷的产品时，也让我们眼花缭乱。在选择最优最适合自己的产品时，每个人在基于了解的产品指标下，对产品进行选择，是大多数人的选择产品的方向。如在选择电脑产品的情况下，对电脑的内存、显卡、系统、处理器等指标进行分析，进而选择合适的产品。本文通过对最优方案选择的角度，切入介绍秩和比评价模型，同时在后文介绍该模型在其他领域的应用。

1 数据选择

本文我们用Python 的随机数生成，在一定范围内生成随机数，制定十个方案，使用三个重要指标对方案进行分析。在模型应用到实际情况下，应认真选择对方案影响最为重要的几个指标进行分析。

2 模型的介绍与建立

2.1 模型的介绍

RSR 最初是由原中国预防医学科学院田凤调教授于1988 年提出的，它是将各种方案依据某些合适的指标加以排序，通过秩变换，获得无量纲秩和比，根据秩和比的值对评价对象的优劣进行排序，之后将各方案分档处理，最后对各方案进行评价。该方法在卫生、经济学等领域的多指标综合评价、统计预测预报等方面已得到广泛的应用。秩和比是一个内涵较为丰富的综合性指标，它是指行 (或列)秩次的平均值，是一个非参数统计量，具有0～1 连续变量的特征。在综合评价中，RSR 综合了多项评价指标的信息,表明多个评价指标的综合水平，RSR 值越大越优[1]。

2.2 秩和比评价模型的建立

每一行(m)为一个被评价对象即方案，每一列(n)为评价指标。

2.3 秩和比评价模型的求解

2.3.1 确立指标

在实际方案中我们应选取对方案最为重要的几个指标进行分析，指标的重要性可以通过主成分分析法进行判断，这里我们不做讨论，直接选出三个指标。分为指标一、指标二、指标三。具体数据如表1 所示：

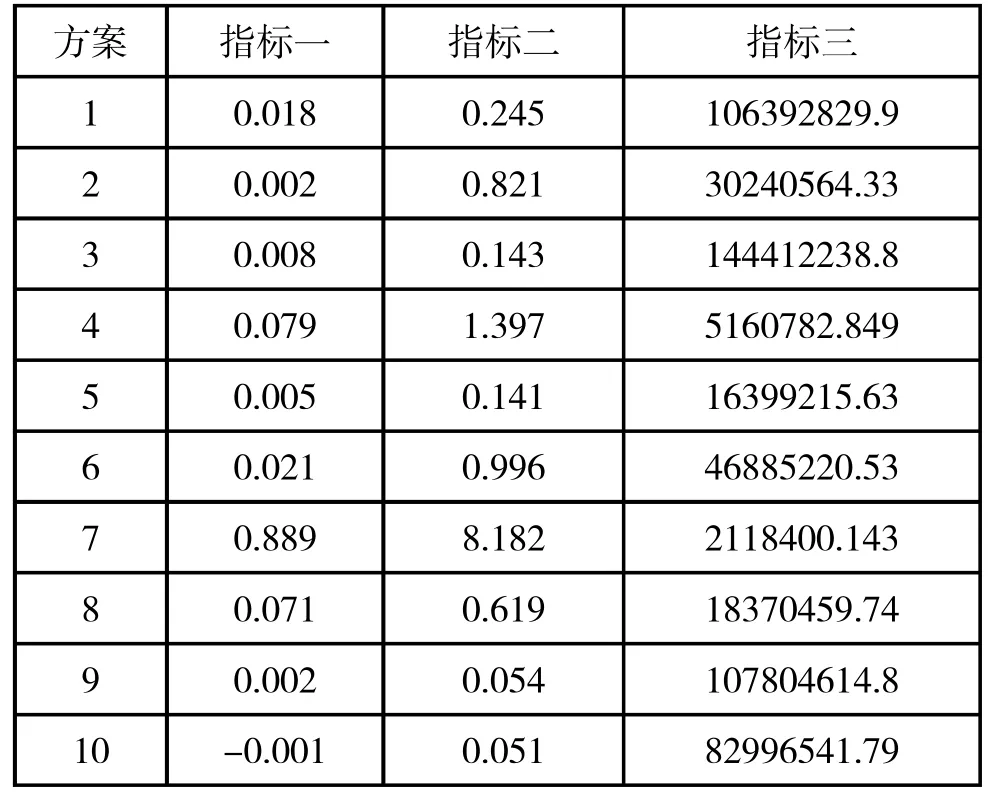
表1 十个方案的三个指标的具体数据

2.3.2 编秩

分别对三项指标从1～10 进行编秩，其中高优指标从小到大编秩，低优指标从大到小编秩，同一指标数据相同者编平均秩。其中高优指标是指对方案有利的指标，指标越大方案越好，低优指标是指对方案不利的指标，指标越小方案越好，结果如表2 所示：

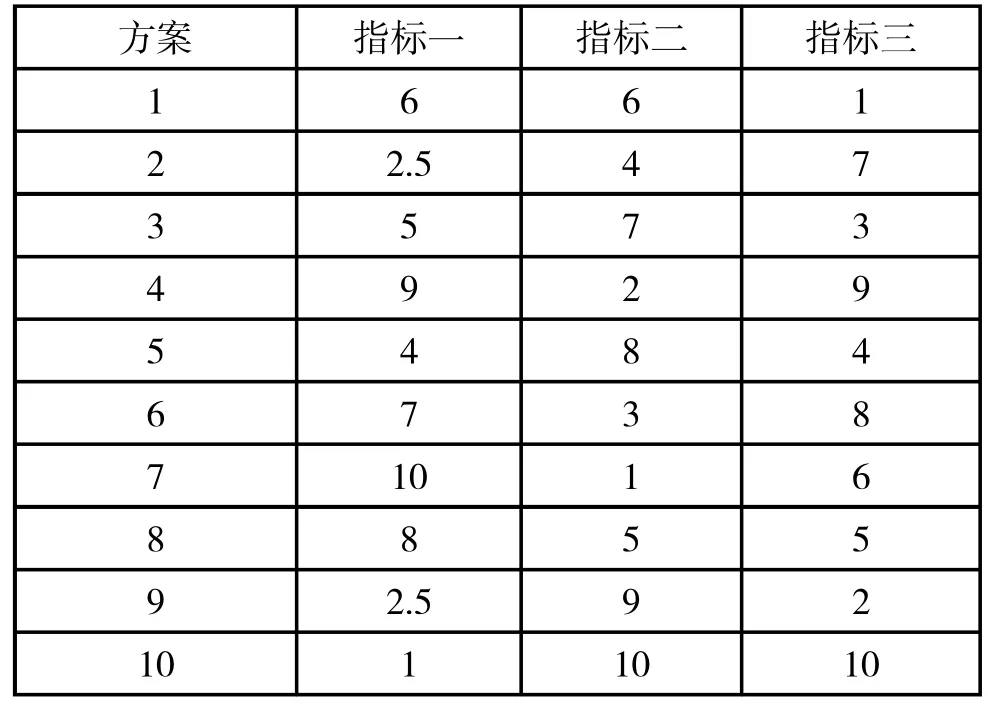
表2 对评价指标的编秩

2.3.3 计算RSR

公式：

其中m=10 n=3（m 为方案数，n 为指标数）

计算结果如表3 所示：

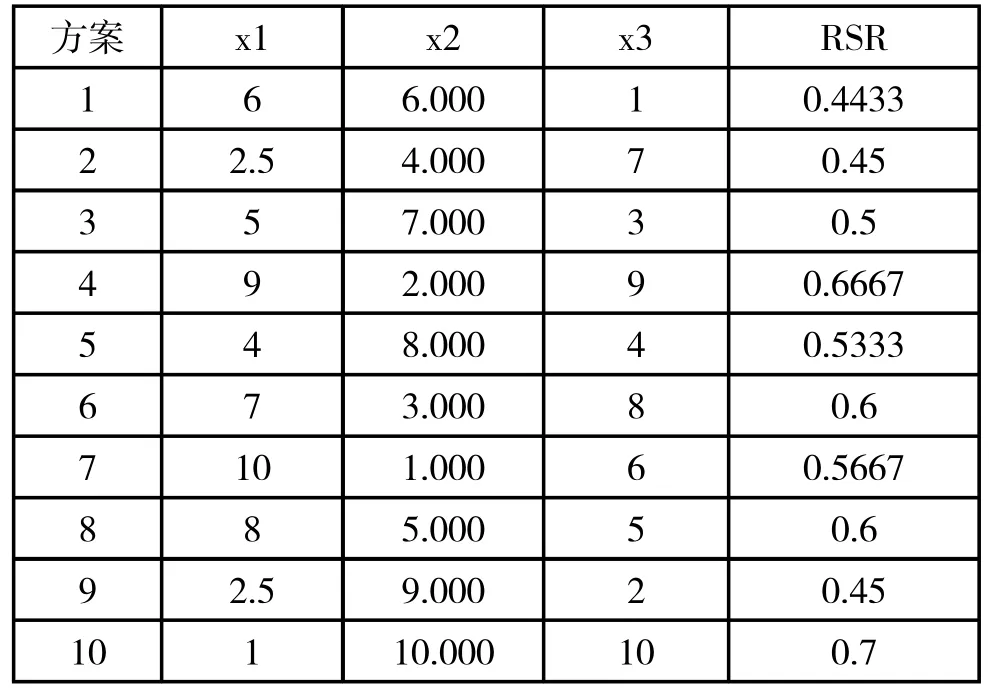
表3 各方案RSR

2.3.4 确定RSR 的分布，计算Probit 概率

将RSR 值由小到大排成一列，相同的作为一组，列出各组频数f 和各组累计频数∑f，确定各组RSR 的秩次范围和平均秩次，计算百分比数p=mean(R)/n，其中mean()为取平均值，再将p 转换为概率单位[2]。转化的具体数据可通过查表得知，如表4 所示

表4 各方案probit 转化

2.3.5 计算直线回归方程

以累计频率所对应的概率单位Probit 为自变量，以RSR为因变量，在MATLAB 中拟合线性回归方程[3]。在软件中得出各系数，求得：RSR=0.06164 * Probit+0.2354。

2.3.6 分档排序

根据Probit 分档，一般分为3～5 档，具体档数应根据具体情况进行讨论分析，在需要对方案进行细分的情况下，建议选择5 档。在本文分析中，这里我们选用3 档，即优、良、差，下表的前两列是常用的分档数对应的概率单位。按照上述回归方程求得分档界值(也就是RSR 预测值)，如表5所示，然后对 RSR 进行排序，并评价各方案，如表6 所示[4]。

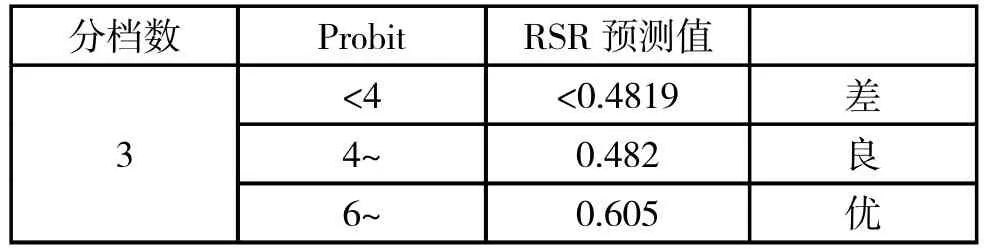
表5 RSR 预测值计算

2.3.7 分档结果

由表6，我们可以得出，根据指标一、指标二、指标三的分析，选出第四个方案与第十个方案是最优的，可以根据此结果进行参考[5]。

3 讨论

秩和比法是一种常用的多指标综合评价方法,近年来已广泛应用于社会医学和卫生事业管理中。在本文中我们笼统的讨论了秩和比评价模型对方案的最优化选择，其中方案可以应用到科技、医学、经济等各个方面的管控决策上。如管控决策的风险评估、最优决策选取等多个方向，下面简单讨论一下在这两个方面该模型的具体应用方式及模型的优缺点。

3.1 评价结论在管理决策中的最优决策选取应用

在对某地区或企业采取新的措施的情况下，可选用秩和比评价模型，对各种措施方案进行分析，选取合适的指标，将措施评价为差的直接删去，在选出为优的几个方案之后，仍可对优等方案再次进行细分，选出最为合适的措施后，在地区或企业上进行试运营，若效果显著，便可正式实行。

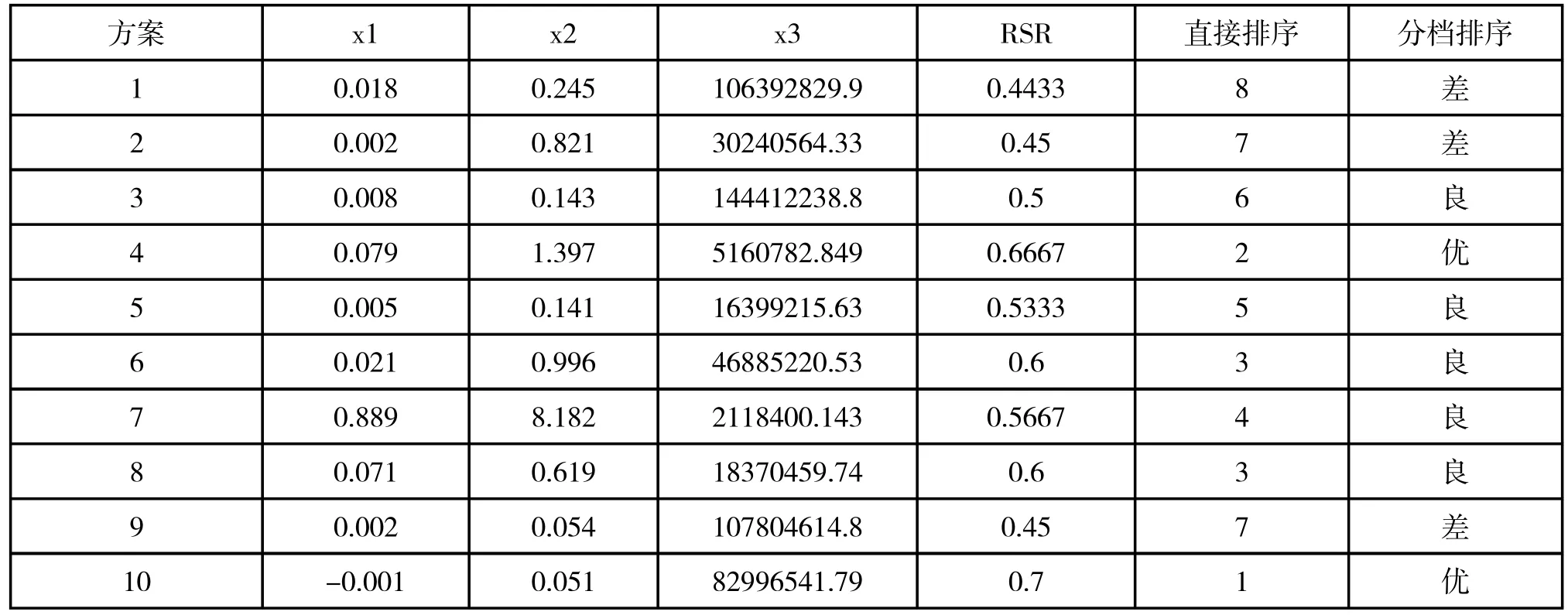
表6 各方案分档排序

3.2 评价结论在管理决策中的风险评估应用

在对某地区的医保基金运行风险进行分析的情况下，可以选用秩和比模型，同样选取分析的各地区的指标，进行风险分析。对评价结果进行分析，对不同运行风险等级的区 (市) 县应采取不同的管控措施。对管控风险等级为高的地区医保经办机构重点加强监控预警与管理,基金管理的行政部门应督促其加强对基金使用的监管;运行风险等级为中的地区医保经办机构不应松懈，应实时根据数据医保数据，严防基金异常使用;运行风险等级为低的地区在上级主管部门对其进行总控考核时，可以对其适当放宽政策，灵活管控[6]。

3.3 模型的优缺点

秩和比综合评价模型的有着明显的优点，运用秩和比法进行统计分析，可以对不同计量单位、多个不同指标进行综合分析，能够全面、合理、客观地反映各方案的实际水平，RSR 值越大反映被评价对象的综合水平越高，秩和比法可以有效消除各个指标之间量纲不同的影响，根据实际情况判断指标的类型，综合计算RSR 值，从而有效地评价各个方案[7]。其运行结果在实际中可行，结论也具有科学性、新颖性和实用性。当然，该模型的指标选取一直是个待商榷的事情，如何选择对评价类型相关的合适指标，对评价结果有些很大的影响，且秩和比法在转化为秩次时损失了一定原始指标的定量信息，其结果反映的也是综合秩次的差距，反映出的结果还不够全面。这种情况也说明了该模型还需要在今后的实践中不断地去完善。