基于DM-LEFM理论的混凝土桥梁受力主筋疲劳全寿命分析

王剑，文国华

基于DM-LEFM理论的混凝土桥梁受力主筋疲劳全寿命分析

王剑，文国华

(湖南城市学院 土木工程学院，湖南 益阳 413000)

混凝土桥梁主筋疲劳全寿命包含裂纹形成寿命和裂纹扩展寿命。鉴于线弹性断裂力学无法估算裂纹形成寿命，提出基于DM-LEFM理论的桥梁主筋疲劳全寿命估算方法。通过损伤力学(DM)估算疲劳裂纹的形成寿命，线弹性断裂力学(LEFM)估算疲劳裂纹的扩展寿命，桥梁的疲劳全寿命即为两者之和。结合龙河特大桥工程，分析估算桥梁受拉主筋的疲劳全寿命。研究结果表明：龙河特大桥疲劳裂纹形成寿命为2.102×105d，大于疲劳裂纹扩展寿命1.041×105d，桥梁疲劳全寿命合计3.143×105d，约861 a。由于损伤力学理论的限制，计算结果未考虑腐蚀对疲劳全寿命的影响，需进一步研究腐蚀对钢筋力学参数的影响。基于DM-LEFM理论的桥梁疲劳全寿命为桥梁疲劳安全评价提供了技术支持。

损伤力学；线弹性断裂力学；疲劳全寿命；混凝土桥梁

现行桥梁设计中已经充分考虑了承载力对结构的影响，然而在桥梁实际运行中的疲劳荷载引起裂纹扩展，并最终导致断裂失效。因此，必须建立一个桥梁的疲劳寿命估算和疲劳安全评价体系。目前，结构疲劳寿命估算通常采用疲劳抗力曲线(S-N)模型、可靠度理论和线弹性断裂力学(LEFM)进行分析[1]。疲劳抗力曲线作为一种常规的疲劳分析方法已被广泛使用。其原则就是使用应力范围或应变范围去评估混凝土构件的疲劳损伤以及剩余寿命[2]。通过引入雨流法或泄水法将应力应变方程拆分为多个应力应变幅和循环次数[3]，并借助疲劳累积损伤理论来预测混凝土结构的疲劳损伤以及剩余寿命。随着结构可靠性理论的不断完善，可靠度理论逐步运用于桥梁疲劳寿命评估[4−5]，通过断裂K判据进行可靠度分析，进而通过确定可靠度计算疲劳寿命。线弹性断裂力学(LEFM)可以有效的进行钢筋混凝土结构的疲劳剩余寿命估算。徐世烺等[6−7]在预测役钢桥的疲劳剩余寿命中采用了确定性断裂力学的评估方法。MA等[8]提出了一个新的裂纹以腐蚀老化对钢筋混凝土梁的疲劳寿命预测方法。桥梁疲劳全寿命周期分为疲劳裂纹形成寿命和疲劳裂纹扩展寿命，线弹性断裂力学已经较好地解决疲劳裂纹扩展寿命的预测问题，但对于出现宏观裂纹前的结构损伤特性无法作出很好的分析。本文使用损伤力学方法和线弹性断裂力学方法分别研究疲劳裂纹的形成和扩展寿命，通过估算的两者寿命之和来确定桥梁主筋疲劳全寿命。

1 桥梁疲劳全寿命周期

桥梁工程中大量的破坏事故是由于疲劳裂纹的扩展引起。由于外荷载与应力随着时间发生交替变化，在交变应力作用下结构产生裂纹并进一步扩展，最终导致结构的疲劳破坏。

大量研究发现[9−10]，当材料或构件内部存在微小裂隙时，若放任其发展，就会合并形成宏观裂痕，而后裂痕不断发展造成材料或构件不可逆转的损伤或断裂。微小裂隙的存在为宏观裂纹的发展埋下了隐患，更有甚者导致结构的整体破坏，这往往会使得材料的力学性能减弱，结构强度达不到预定要求，使用年限随之锐减。

因此，桥梁主筋疲劳全寿命周期应考虑疲劳裂纹产生和扩展2个阶段，并分别估算过程时间。损伤力学(DM)是固体力学的重要分支，利用宏观力学分析断裂的微观特征。其主要研究对象为结构内连续存在的各类杂质、微裂缝、微空洞等，即结构损伤。因此，可以采用损伤力学理论分析桥梁结构中裂纹产生过程和规律，计算裂纹产生期的疲劳寿命。线弹性断裂力学(LEFM)的研究对象集中于裂纹尖端区域，通过分析该区域的应力、应变规律，用以宏观定量解决结构的缺陷与断裂问题。对于疲劳裂纹扩展寿命常采用该理论进行分析[11]。因此基于DM-LEFM理论，可以进行桥梁主筋疲劳全寿命的分析与计算。

2 桥梁疲劳裂纹形成寿命估算

2.1 损伤变量

Kachnov认为因材料缺陷引起有效承载面积减少是其劣化的主要原因，因此提出了材料损伤参数−连续度[12]：

对上述连续度进行改进，采用损伤度用于描述材料损伤[13]。

2.2 损伤本构及演化模型

Lemaitre认为有效应力可以完全体现材料变形行为，因此无损材料中由有效应力引起的应变，与柯西应力引起的损伤材料应变是等价的[14]。就此推导了损伤材料的本构模型：

即，

式中：和分别为材料的弹性模量和应变。

损伤发展过程中材料裂面急剧增加，过程伴随能量释放，最终形成损伤演化这一种不可逆的劣化过程。以等效应力建立的损伤演化方程为：

式中：表示应力循环次数；，和均为拟合参数，取决于材料的疲劳性能曲线，反映了材料的疲劳损伤特性；为应力循环的等效应力。

为简化计算，认为桥梁材料服从各向同性和线弹性损伤条件。则损伤演化方程简化为：

2.3 形成寿命分析

当桥梁主筋处于临界损伤点时，即=c，则临界损伤方程为：

将损伤本构方程式(3)代入式(7)，可得：

桥梁主筋无损伤时，=0且c=0，在疲劳作用下桥梁主筋形成裂纹。因此，先对式(8)进行积分，再将c=1时代入积分公式中求出对应的N。

通过求解式(9)中的和2个待定参数，即可估算疲劳裂纹形成寿命N。

3 疲劳裂纹扩展寿命估算

3.1 初始裂纹

确定桥梁主筋的初始裂纹是采用线弹性断裂力学(LEFM)对桥梁寿命估算的重要步骤。通常，采用直接观察法或假定法确定。对于钢结构桥梁，裂纹比较容易观察时，可以采用无损探伤方式确定裂纹的初始位置及形态特征。对于钢筋混凝土桥梁，由于结构不规则及隐蔽性，导致裂纹不易观测或监测，只能通过合理假设确定。可以依据式(10)设计一个初始裂纹，再进行疲劳裂纹寿命分析。

式中：0为初始裂纹宽度；Δ为最大应力幅；Δth为钢筋裂纹扩展阈值；

3.2 断裂类型及临界裂纹

在应力作用下，初始裂纹逐步扩展到某一阈值时，钢筋混凝土构件便会发生断裂损坏。钢筋损坏的2种主要形式为脆断和韧断。根据线弹性断裂力学的准则，水平应力断裂韧性和平面应变断裂韧性之间满足>IC的关系，通常根据关系式≥IC判断混凝土构件是否遭到破坏。为应子强度因子，IC为材料断裂韧度。

当桥梁主筋发生脆性断裂时，临界裂纹宽度为：

式中：sup为恒荷载与活荷载之和；cr为几何修正系数。

Herwig等[15]研究发现应力强度因子的几何修正系数近似满足如下公式：

当桥梁主筋发生韧性断裂时，裂纹半宽度0随着应力的加载，其裂纹半宽度增加至y，y表示钢筋屈服裂纹扩展后的半宽度。临界裂纹宽度为：

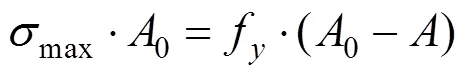
式中：为混凝土构件横截面面积减少值；y为混凝土构件在承受应力作用时所达到的屈服强度；0是钢筋最初始的横截面积值；max为构件发生疲劳破坏时钢筋所承受的最大应力。

因此，选择临界裂纹深度fr为上述两者中的较小值：

3.3 扩展寿命分析

在研究疲劳裂纹扩展时，假定裂纹扩展只是由于初始裂纹引起的，而忽略其他因素。根据这一假定，应力强度因子和裂纹扩展的关系满足Paris- Erdogan公式[16]：

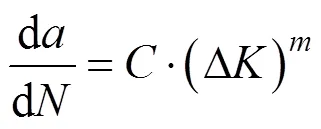
式中：和均是与材料相关的参数，不随结构的形状和荷载性质而改变；Δ为应力刚度因子。

根据式(16)，当裂纹深度由0扩展到fr的循环数N即为疲劳裂纹扩展寿命：

4 实例分析

4.1 工程概况

龙河特大桥位于重庆市涪陵区，全长1 181 m，属于涪陵至丰都高速公路建设的重点工程。龙河特大桥全桥共有六联构成，其中龙河特大桥的主桥设计采用变截面预应力混凝土连续刚构箱梁。桥梁受力主筋为Φ22的Ⅱ级钢筋，其半径是8 mm，屈服强度y为335 MPa，大桥竣工前如图1所示。

4.2 初始裂纹估算

龙河特大桥为钢筋混凝土公路桥，裂纹不易观测，只能通过假定法进行估算。桥梁受力主筋为Φ22的Ⅱ级钢筋，其半径是8 mm。根据龙河特大桥主筋类型，类比文献[12]数据，公路桥梁钢筋裂纹扩展阈值取为Δth=90 MPa∙mm1/2，应力幅Δ最大值取为45 MPa。采用式(10)可估算本文案例桥梁的初始裂纹宽度为：

4.3 裂纹形成寿命估算

采用龙河大桥疲劳试验结果，对式(9)进行最小二乘拟合，获得材料参数=2.03×10−9，=2.79。桥梁的初始裂纹宽度0=1 mm，根据拟合的材料参数，由式(9)计算在最大应力幅45 MPa条件下的裂纹形成寿命，即达到初始裂纹深度为0=1 mm的应力循环次数，结果如表1所示。

4.4 临界裂纹估算

当桥梁主筋发生脆性断裂时，选取断裂韧度IC=3 000 MPa·mm1/2，由式(11)和式(12)可计算得临界脆断裂纹宽度cr如表1所示。

表1 龙河特大桥主筋疲劳全寿命估算结果

当桥梁主筋发生韧性断裂时，临界韧断裂纹宽度y可由式(13)～(14)计算得到，如表1所示。

4.5 裂纹扩展寿命估算

根据Paris-Erdogan公式，该桥梁钢筋材料常数=2×10−13，=4。则裂纹的扩展寿命为初始裂纹宽度0=1 mm到临界裂纹宽度fr=9.12 mm的应力循环次数。式(17)可以计算裂纹扩展寿命。然而对Paris-Erdogan公式直接积分，只考虑了应力幅，结果偏于安全。根据几何修正因子式(12)和应力刚度因子式(17)对Δ和Δth进行比较。Δ＞Δth则表示裂纹发生扩展，Δ＜Δth则裂纹未扩展。为此，通过分析裂纹的扩展量Δ，则下一循环的裂纹宽度为a+1=a+Δ，将新的裂纹长度带入应力幅水平计算公式中便可以计算出应力强度因子幅、应力强度因子、裂纹的扩展量以及循环的裂纹长度。

采用MATLAB进行桥梁裂纹扩展寿命估算流程如图2所示。

图2 裂纹扩展寿命估算流程

5 结论

1) 线弹性断裂力学方法不能估算疲劳裂纹全寿命，通过引入损伤力学理论估算疲劳裂纹形成寿命。将损伤力学(DM)与线弹性断裂力学(LEFM)相结合，提出了桥梁主筋疲劳全寿命估算方法。

2) 通过对龙河特大桥主筋疲劳全寿命估算，体现了该方法的可操作性。研究表明桥梁主筋疲劳裂纹形成寿命远大于扩展寿命，桥梁疲劳安全评价因充分考虑桥梁疲劳全寿命周期。

3) 本文中采用DM-LEFM理论计算龙河特大桥受拉主筋的疲劳全寿命为3.143×105d，约861年，由于损伤力学理论的限制，无法考虑腐蚀条件对桥梁疲劳全寿命的影响。腐蚀作为钢筋损失及断裂的重要影响因素，如何在桥梁疲劳全寿命计算考虑钢筋腐蚀有待进一步地研究。

[1] 李少骏. 中小跨径混凝土桥梁疲劳荷载模型及疲劳性能研究[D]. 杭州: 浙江大学, 2015.LI Shaojun. Fatigue load model and fatigue behavior of medium & short span concrete bridges[D]. Hangzhou: Zhejiang University, 2015.

[2] 周虎, 肖勇刚, 谭斌. 基于断裂力学的混凝土桥梁疲劳损伤及寿命评估分析[J]. 湖南城市学院学报(自然科学版), 2018, 27(4): 6−10.ZHOU Hu, XIAO Yonggang, TAN Bin. Fatigue damage and life evaluation of concrete bridges based on fracture mechanics[J]. Journal of Hunan City University (Natural Science), 2018, 27(4): 6−10.

[3] 张慧梅. 断裂力学[M]. 徐州: 中国矿业大学出版社, 2018. ZHANG Huimei. Foundation of fracture theory[M]. Xuzhou: China University of Mining and Technology Press, 2018.

[4] 杨晓红. 基于可靠度理论的钢桥剩余疲劳寿命评估[D].镇江: 江苏大学, 2006. YANG Xiaohong. Remaining fatigue life assessment of steel bridges based on reliability theory[D]. Zhenjiang: Jiangsu University, 2006.

[5] 朱金, 吴梦雪, 尹力, 等. 随机车流−风联合作用下沿海大跨度斜拉桥拉索疲劳寿命预测研究[J]. 中国公路学报, DOI:61.1313.U.20200427.1020.008.ZHU Jin, WU Mengxue, YIN Li. Fatigue life prediction on cables of coastal long-span cable-stayed bridges under stochastic traffic and wind loads[J].China Journal of Highway and Transport, DOI:61.1313.U.20200427.1020. 008

[6] 徐世烺. 混凝土断裂力学[M]. 北京: 科学出版社, 2011. XU Shilang. Fracture mechanics of concrete[M]. Beijing: Science Press, 2011.

[7] GOU S H, ZHAN G Y, YIN X F. Analysis on vehicle-bridge coupling vibration of FRP deck and steel girders bridge[J]. Applied Mechanics and Materials, 2013, 361(1): 1339−1343.

[8] MA Y, XIANG Y, WANG L, et al. Fatigue life prediction for aging RC beams considering corrosive environments [J]. Engineering Structures, 2014(79): 211− 221.

[9] 李庆斌. 混凝土断裂损伤力学[M]. 北京: 科学出版社, 2017. LI Qingbin. Fracture and damage mechanics of concrete [M]. Beijing: Science Press, 2017.

[10] Ghidini T, Dalle D C. Fatigue life predictions using fracture mechanics methods[J]. Engineering Fracture Mechanics, 2009, 76(2): 134−148.

[11] 吴圣川, 李存海, 张文, 等. 金属材料疲劳裂纹扩展机制及模型的研究进展[J]. 固体力学学报, 2019, 40(6): 489−538. WU Shengchuan, LI Cunhai, ZHANG Wen, et al. Recent research progress on mechanisms and models of fatigue crack growth for metallie materials[J]. Chinese Journal of Solid Mechanics, 2019, 40(6): 489−538.

[12] 王春生, 周江, 吴全有, 等. 既有混凝土桥梁疲劳寿命与使用安全评估[J].中国公路学报, 2012, 25(6): 101− 107. WANG Chunsheng, ZHOU Jiang, WU Quanyou, et al. Fatigue life and service safety assessment for existing concrete bridges[J]. China Journal of Highway and Transport, 2012, 25(6): 101−107

[13] Simpson C A, Kouzuki S, Lopez-crespo P, et al. Quantifying fatigue overload retardation mechanisms by energy dispersive X-ray diffraction[J]. Journal of the Mechanics and Physics of Solids, 2018, 124: 392−410.

[14] 郑旭东, 张行. 预估金属构件疲劳全寿命的损伤力学−有限原法[J].航空学报, 1991, 12(2): B1−B9. ZHENG Xudong, ZHANG Xing. Damage mechanics finite element method for prediction of total fatigue lives of metal structure members[J]. Acta Aeronautica Et Astronautica Tica Sinica, 1991, 12(2): B1−B9.

[15] Herwig A, Motavalli M. Load-carrying capacity of GFRP bars under combined axial force-transverse force loading [J]. Composites, 2013, 44(1): 167−171.

[16] 勾红叶,许会燕,李凯强, 等. 基于次序定律的既有铁路桥梁新疲劳寿命评估方法[J]. 土木工程学报, 2015, 48(9): 76−84. GOU Hongye, XU Huiyan, LI Kaiqiang, et al. Study of a new assessment approach of fatigue life based sequential law for existing railway bridges[J]. China Civil Engineering Journal, 2015, 48(9): 76−84.

Life-cycle fatigue analysis of main reinforcements of the concrete bridge based on the DM-LEFM theory

WANG Jian, WEN Guohua

(College of Civil Engineering, Hunan City University, Yiyang 413000, China)

Life-cycle fatigue development of main reinforcements of the concrete bridge includes crack initiation and crack propagation. Since the linear elastic fracture mechanics is incapable of estimating crack formation life, the DM-LEFM theory was proposed to calculate the fatigue life for the concrete bridge. The damage mechanics (DM) was applied to deal with the crack initiation life, while the linear elastic fracture mechanics (LEFM) was used for the estimation of crack propagation life. In combination with the engineering project of the Long River Bridge, the life-cycle fatigue analysis of the main reinforcements was performed. Results show that the crack initiation life for the Long River Bridge is 2.102×105 days, and the crack propagation life is 1.041×105 days, thus the fatigue life should be 3.143×105 days, about 861 years. Due to the limitation of damage mechanics, the results are unable to take corrosion into consideration, thus further study should be carried out to analyze the impact that corrosion has on mechanical parameters of steel components. The idea of life-cycle fatigue analysis based on the DM-LEFM theory could provide technical support to the safety evaluation for concrete bridges.

damage mechanics; linear elastic fracture mechanics; total fatigue life; concrete bridge

TU448.13

A

1672 − 7029(2020)10 − 2597 − 06

10.19713/j.cnki.43−1423/u.T20200599

2020−06−29

湖南省教育厅科研资助项目(15C0256)

文国华(1960−)，男，湖南常德人，教授，从事桥梁结构理论分析研究；E−mail：kkk161@163.com

(编辑 蒋学东)