基于I＆I 理论的可逆冷带轧机速度张力系统自适应分散控制①

刘 乐， 丁素艳， 高 杰， 方一鸣

（1.燕山大学 工业计算机控制工程河北省重点实验室，河北 秦皇岛066004； 2.智能控制系统与智能装备教育部工程研究中心，河北 秦皇岛066004）

可逆冷带轧机是生产特种钢、普通碳钢等带钢产品的专用设备［1］，在轧制生产中，其左卷取机、主轧机和右卷取机通过带钢挠性连接在一起，三者构成了一个具有多变量、非线性、强耦合和不确定特征的复杂动态系统［2］。 国内外学者针对冷带轧机速度张力系统的跟踪控制问题进行了大量研究［3-6］，但这些控制器设计方法大部分需要构造Lyapunov 函数，在某种程度上增加了系统控制器设计的复杂度。 Astolfi 和Ortega 提出的浸入与不变（immersion and invariance，I＆I）理论是一种较新颖的自适应控制方法［7］，它无需构造Lyapunov 函数，不仅能够处理非线性系统的控制问题，还能够处理系统中不确定参数的自适应问题。 本文基于I＆I 理论提出了一种冷带轧机速度张力系统自适应分散控制方法，实现了冷带轧机速度张力系统的分散跟踪控制，并具有较好的动态、静态性能。

1 可逆冷带轧机速度张力系统模型

可逆冷带轧机主要由左卷取机、主轧机、右卷取机和导向辊等组成，具有结构简单、投资少、运行成本低等优点，适用于不同产品规格的小批量生产。 可逆冷带轧机速度张力系统的数学模型［1］为：

式中sys1，sys3分别为左、右卷取机张力子系统，sys2为主轧机速度子系统；Bui为摩擦系数，kg·m2／s；ηi为减速比；Vi为线速度，m／s；Ki为电机的转矩系数，N·m／A；Ji为转动惯量，kg·m2；ui，Ksi分别为可控硅整流装置的控制电压（V）和放大倍数；Ii，ri和li分别为电枢回路的电流（A）、电阻（Ω）和电感（H）；E为杨氏弹性模量，N／m2；R1，R3分别为左、右卷取机钢卷的半径，m；R2为主轧机工作辊的半径，m；F1，F3分别为主轧机两侧的带钢张力，N；A1，A2分别为主轧机两侧的带钢截面积，m2；δ0，χ0分别为无张力时的前、后滑系数；Kδ，Kχ分别为张力对前、后滑的影响系数；B，ρ分别为带钢的宽度（m）和密度（kg／m3）；H，h分别为主轧机两侧的带钢厚度，m；L为主轧机与左、右卷取机间的距离，m；Mz为主轧机的轧制力矩，N·m；Δ2＝ΔBu2V2／J2＋ΔMzR2／（J2η22），为系统参数摄动ΔBu2和负载扰动ΔMz引起的非匹配不确定项，m／s2。

为方便起见，文中下脚标i＝1，2，3 分别表示sys1，sys2和sys3的相关参数。

2 非匹配不确定项的SMO 设计

考虑到SMO 方法构造简单且观测精度高［8］，因此，为了削弱Δ2对系统性能的影响，本文采用SMO 方法对其进行动态观测。 假设Δ2的变化率满足其中μ2＞0。 SMO 的具体构造形式如下：

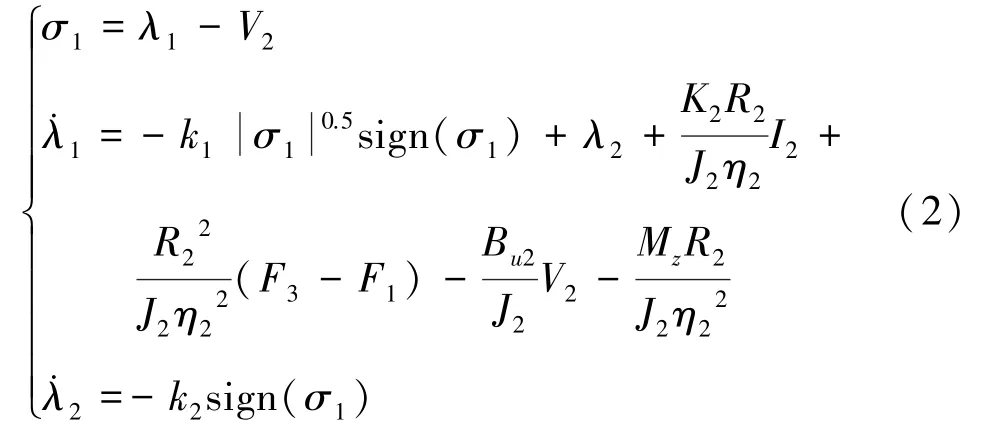
式中λ1为V2的观测值；λ2为非匹配不确定项Δ2的观测值；σ1为λ1对V2的观测误差；k1，k2均为观测器的调节参数，并且满足k1＞0，k2＞μ2。

结合文献［9］和［10］可知，式（2）所构造的SMO是有限时间稳定的。

3 基于I＆I 理论的摄动参数估计器设计

假设相对于参数估计器的动态特性，摩擦系数Bu1，Bu3是慢时变的，即̇Bu1＝̇Bu3≈0。

首先，定义参数估计误差：

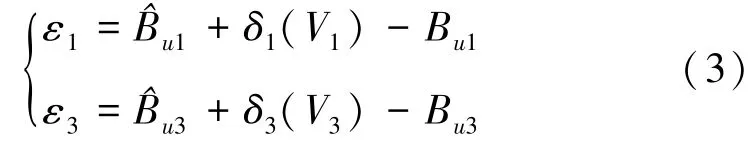
式中＾Bu1＋δ1（V1），＾Bu3＋δ3（V3） 分别为Bu1，Bu3的估计值；δ1（V1）和δ3（V3）均为待设计的调节函数。

将参数估计误差ε1，ε3所对应的流形面定义为：

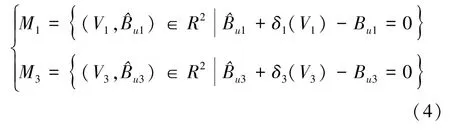
结合式（1），将摩擦系数Bu1，Bu3的自适应律分别设计为：

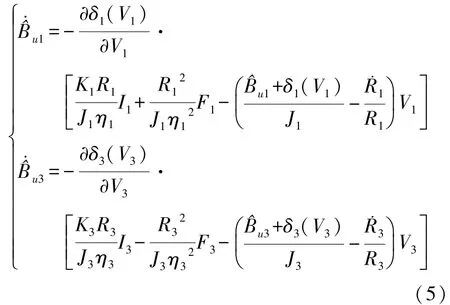
将调节函数δ1（V1），δ3（V3）分别取为：

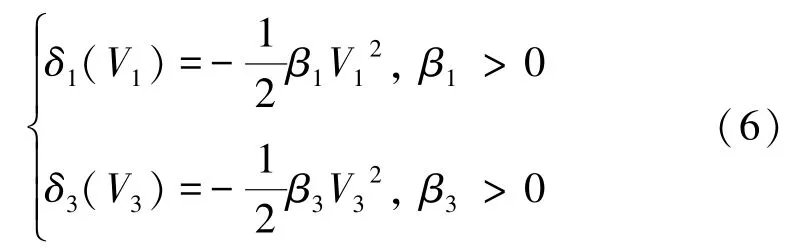
由式（8）可知，参数估计误差ε1，ε3是渐近稳定的，且能够以指数规律单调收敛至原点，即：

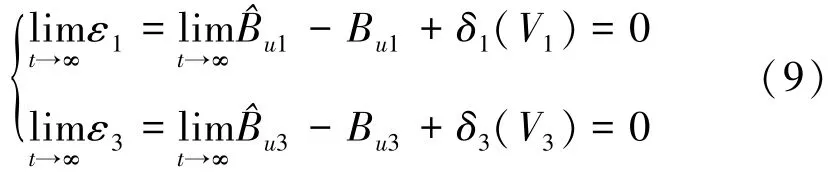
在I＆I 自适应方法中，系统的摄动参数Bu1，Bu3分别用＾Bu1＋δ1（V1），＾Bu3＋δ3（V3）来估计，其中调节函数δ1（V1），δ3（V3）的引入使得参数自适应律由单一的积分作用转变为比例积分作用，突破了传统自适应方法所遵循的确定等价原则，增加了参数估计器设计的灵活性。 且在I＆I 自适应方法中，将摄动参数的估计值和真实值之间的差值作为不变流形M1，M3，通过保持该流形的不变与吸引性，可以保证参数估计误差收敛至原点。

4 基于I＆I 理论的分散控制器设计

4.1 系统模型变换

考虑到基于I＆I 理论的非线性控制器设计方法需采用系统模型的误差形式，故对于系统模型（式（1））定义误差变量：

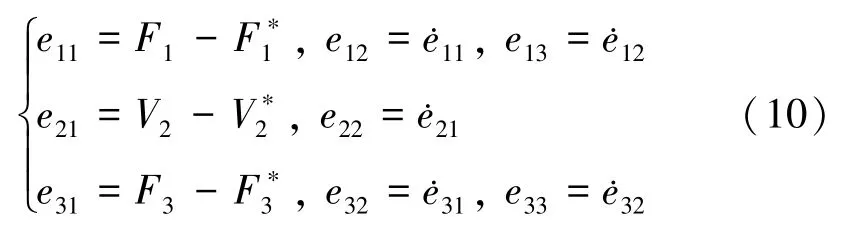
则可将系统模型（式（1））变换为如下误差形式：

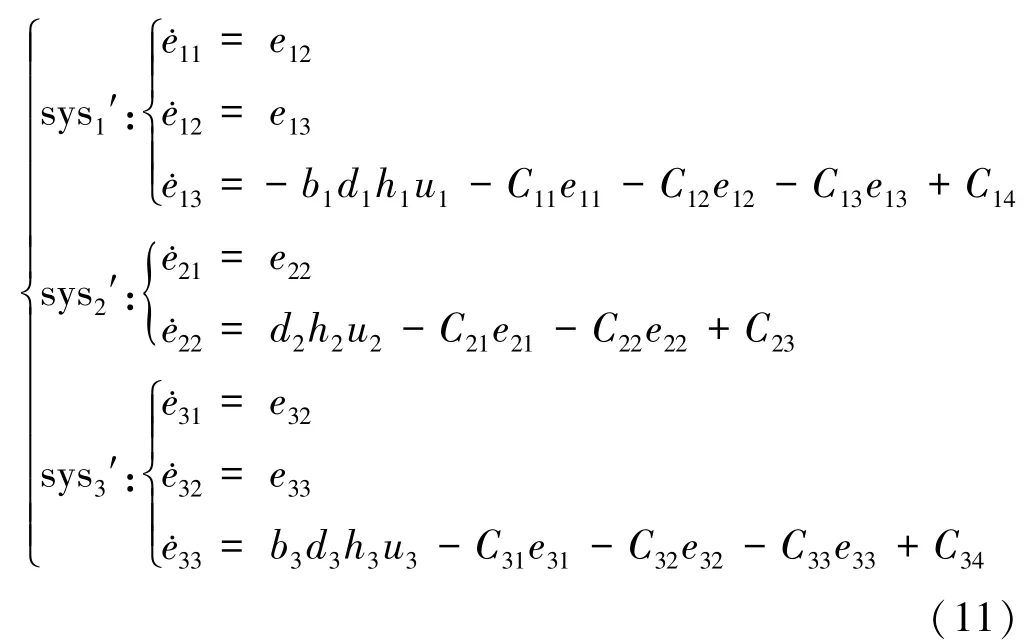
4.2 基于I＆I 理论的左卷取机张力子系统控制器设计

基于I＆I 理论［7］的左卷取机张力子系统控制器u1的设计步骤具体如下：

步骤1（目标系统）：选取一个比sys1′（式（11））维数低且稳定的目标系统。 这里定义一个二阶目标系统：

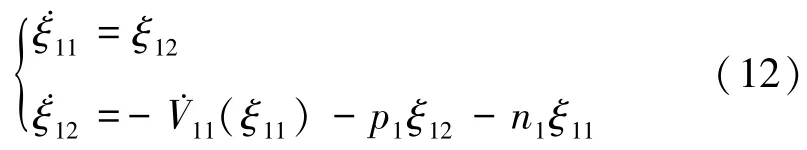
步骤2（浸入条件）：考虑系统的控制目标及目标系统动态，将映射Π1（ξ1）选择为：

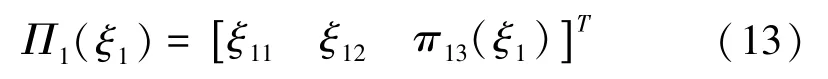
式中π13（ξ1）为待设计函数。

由式（14）的第一行可以进一步得出：

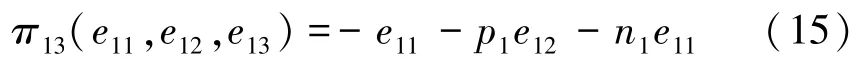
步骤3（隐式流形）：流形M11的隐式描述为：

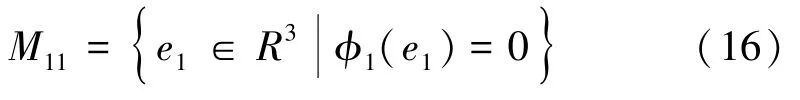
其中φ1（e1）＝e13-π13（e11，e12，e13）＝e13＋e11＋p1e12＋n1e11。

步骤4（流形吸引性和轨迹有界性）：定义偏流形坐标z1＝φ1（e1），并求其时间导数：

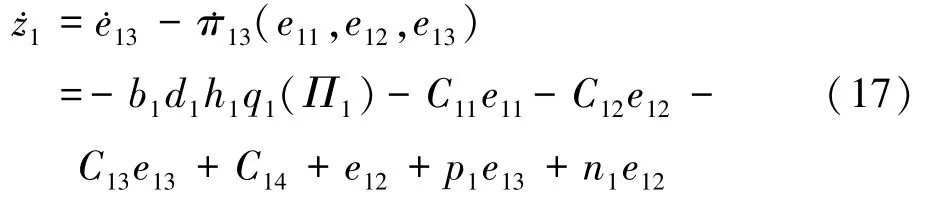
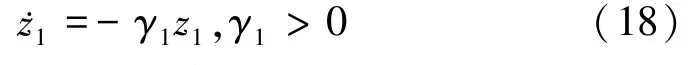
则由式（17）和式（18）可以求得：

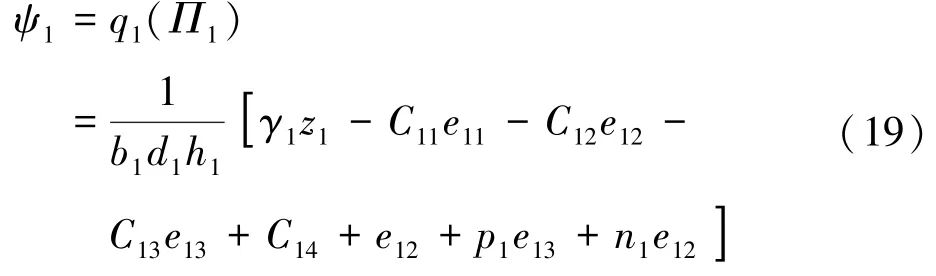
即基于I＆I 理论的左卷取机张力子系统控制器u1可设计为：

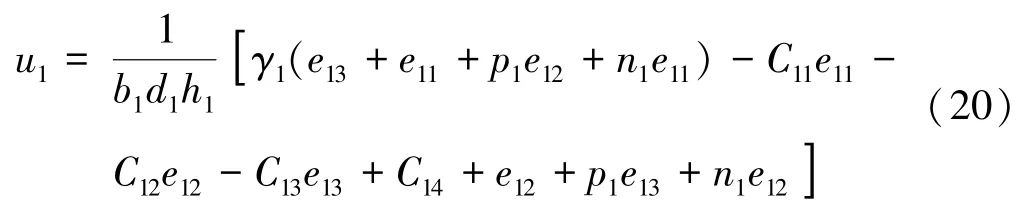
4.3 基于I＆I 理论的主轧机速度子系统控制器设计

参照基于I＆I 理论的左卷取机张力子系统控制器u1的设计步骤，可将主轧机速度子系统sys2′的一阶目标系统、能量函数V21（ξ21）、映射Π2（ξ2）、流形M22和控制器u2分别选取／设计为：

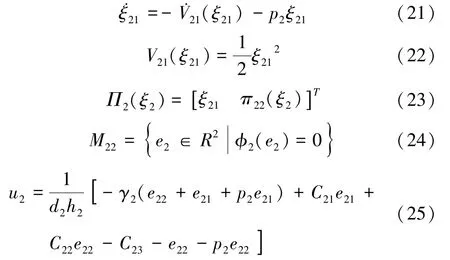
式中p2＞0，为阻尼系数；γ2＞0，为待设计参数。

4.4 基于I＆I 理论的右卷取机张力子系统控制器设计

同理，参照基于I＆I 理论的左卷取机张力子系统控制器u1的设计步骤，可将右卷取机张力子系统sys3′的二阶目标系统、能量函数V31（ξ31）、映射Π3（ξ3）、流形M33和控制器u3分别选取／设计为：

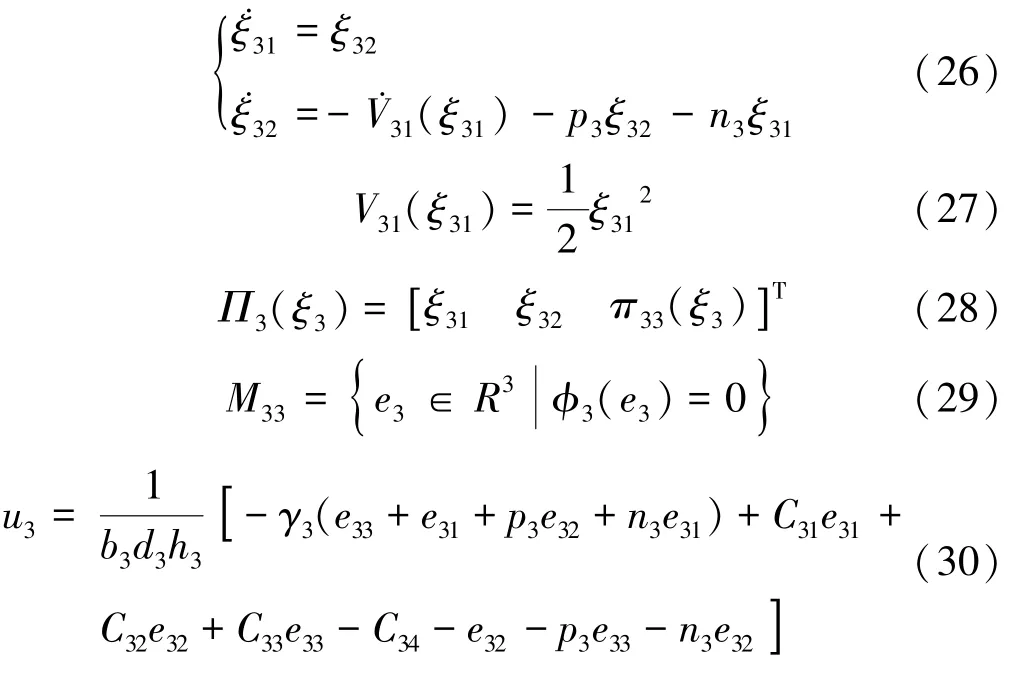
式中p3，n3＞0，为阻尼系数；γ3＞0，为待设计参数。

I＆I 控制器设计方法与目前大多数控制器设计方法有所不同，原则上它不需要构造Lyapunov 函数，比较适用于能够对降阶系统设计稳定控制器的情形。 此外，I＆I 控制器设计方法将被控系统完全浸入到降阶的目标系统中，并利用流形的不变性来保证整个系统的稳定性。

基于I＆I 理论的自适应控制器设计方法包括参数估计器和控制器两个模块，二者彼此相互独立，可以分别进行设计，便于系统控制参数的调整。

5 仿真研究

基于某1 422 mm 可逆冷带轧机速度张力系统的实际数据，将本文所提方法与I＆I 控制方法和反步动态面控制方法进行了仿真对比研究。

选用某一轧制规程的实际轧制参数为：R1＝0.89 m，R2＝0.206 35 m，R3＝0.255 m；J1＝3 347 kg·m2，J2＝1 274.5 kg·m2，J3＝406.7 kg·m2；Mz＝25 kN·m；E＝2.508×109N／m2；L＝3 m；H＝2.06×10-3m，h＝1.582×10-3m；B＝1.25 m；Bu2＝0.569 9 kg·m2／s，Bu1＝Bu3＝0.301 4 kg·m2／s；r1＝r3＝0.021 Ω，r2＝0.015 9 Ω；l1＝l3＝1.38×10-3H，l2＝1.28×10-3H；η1＝η3＝1.807，η2＝1；Ks1＝Ks3＝108，Ks2＝135.1；δ0＝0.065，χ0＝0.182，Kχ＝6.511×10-8，K1＝K3＝23.674 9 N·m／A，K2＝32.608 9 N·m／A；Kδ＝5×10-8。

为便于仿真研究，假定可逆冷带轧机速度张力系统（式（1））中的摩擦系数Bui在t＝9 s 时刻发生摄动变为1.2Bui，负载扰动ΔMz＝2 500 sin（t）N·m（在系统负载±10%的范围内变化）。

本文所提方法的主要参数取为：k1＝5，k2＝8 000，k3＝1 000；β1＝550，β2＝80；γ1＝2 000，γ2＝2 000，γ3＝2 000；p1＝p3＝200，p2＝300；n1＝n3＝1 500。

模拟可逆冷带轧机某一道次的轧制工序：首先在0～2.5 s 时间内分别将左卷取机张力升至100 kN，右卷取机张力升至120 kN，以建立主轧机两侧的带钢张力；然后在2.5～5 s 时间内将主轧机速度升至3.5 m／s后开始正常的轧制生产工艺；在t＝10 s 时刻，将主轧机速度降至0 m／s，左、右卷取机张力保持不变，该道次轧制完成。 此外，为了防止主轧机轧制速度变化过快对轧机设备产生冲击，本文对主轧机速度的给定斜率进行了限制：amax，min＝±3 m／s2。

可逆冷带轧机速度张力系统跟踪控制曲线如图1所示。

从图1（a）～（c）可以看出： ①在反步动态面控制方法的作用下，F1，V2和F3这3 个输出变量实现了对系统给定值F1∗，V2∗和F3∗的跟踪控制，然而系统的稳态精度较差，抗干扰能力较弱； ②在本文所提控制方法的作用下，F1，V2和F3这3 个输出变量不仅实现了对系统给定值F1∗，V2∗和F3∗的跟踪控制，而且系统的稳态精度较高，抗干扰能力较强。

从图1（b）、（d）和（e）可以看出： ①在正常轧制阶段，主轧机的轧制速度高于左卷取机速度而低于右卷取机速度，使得主轧机两侧产生带钢张力，便于轧制过程的顺利进行； ②在本文所提控制方法的作用下，左、右卷取机动态响应迅速，运行相对平稳。

图2 为摩擦系数Bu1，Bu3的估计值曲线。 由图2可以看出：所设计的I＆I 参数估计器对摩擦系数Bu1，Bu3实现了有效地估计，进而可将估计值引入所设计的I＆I 分散控制器中进行补偿，以使系统能够根据摄动参数的变化自行调整。

图3 为SMO 的观测值曲线。 由图3 可以看出：所构造的SMO 对系统的非匹配不确定项Δ2进行了有效地动态观测，进而可将观测值引入到所设计的I＆I分散控制器中进行补偿，提高了系统的跟踪控制精度。

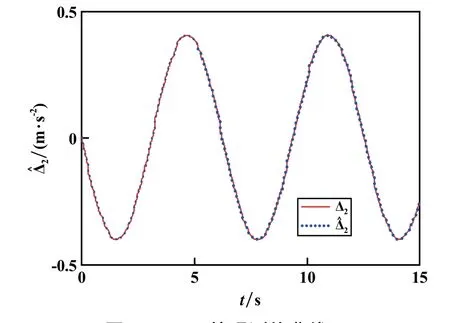
图3 SMO 的观测值曲线

6 结 论

1） 通过构造SMO 对系统的非匹配不确定项进行动态观测，有效地提高了系统的控制精度； 通过设计I＆I 参数估计器对系统的摄动参数进行自适应估计，突破了传统自适应方法遵循的确定等价原则，且其参数估计误差能以指数规律的形式单调收敛至原点。

2） I＆I 控制器的设计过程简洁，可调参数少，且无需构造Lyapunov 函数，实现了可逆冷带轧机速度张力系统的分散控制。

3） 基于某1 422 mm 可逆冷带轧机实际数据的仿真对比结果表明： 可逆冷带轧机速度张力系统在本文所提控制方法的作用下具有较好的动态、静态性能，以及较强的鲁棒稳定性能。