本轮猪周期主因非洲猪瘟量化模型设计及价格预测效果评估

杨 雪 李文献

（1武汉中育科技有限公司，湖北武汉 430070；2河南龙凤山股份有限公司，河南驻马店463000）

1 引言

1.1 模型设计背景

我国居民饮食习惯决定国内生猪消费以“鲜肉”为主，生猪产业链从生猪养殖到活猪屠宰最后到猪肉产品送达餐桌，即从供应端直接到达需求端，因而影响供需平衡的生产、需求、库存3个因素里面的库存因素对供需调节的影响很小，由此可以假设生猪供应量约等于消费需求量。随着我国宏观经济增长和居民收入水平提高，生猪价格的需求弹性越来越小，目前我国约5 500万吨的年猪肉消费需求量，已经让供应端的收入接近边际成本，因此需求的刚性增加已经不足以引起强有力的价格波动进而推动新一轮猪周期的产生，只有当某一因素影响到供应端生产效率导致供应不足，才有可能引发一轮猪周期。本轮猪周期就是由于2018年8月以来非洲猪瘟疫情严重影响生猪生产效率，从而引发的生猪价格大幅波动，同时这也是自20世纪90年代以来6轮猪周期中价格波动最强的一次。通过分析引起本轮猪周期的主因非洲猪瘟内在逻辑对供应影响的规律，从而达到预测本轮猪周期价格规律的目的。

1.2 模型涉及名词解释

主因强度因子（Strength，简称S）：根据主因的流行病学规律，分析主因发生后在未来持续作用的几个月内每个月的作用强度。

主因时间因子（Time，简称T）：根据生猪繁殖周期、MSY等生猪生产技术指标及主因发生后的复养时间，分析在不同生产模式下，主因发生后在未来一段时间内的生猪减产复产周期以及生猪出栏减少量的规律。

分配函数（Φ）：根据主因强度因子（S）和时间因子（T）双维度分配结果，总结主因导致的生猪出栏减少量分配至未来各月的规律的函数。

量价运算框（Operation box）：分析生猪出栏减少量和生猪价格关系规律的运算模型，按输入与输出变量不同，可分为P-Y量价运算框（输入实际生猪价格，输出生猪出栏减少量估计理论值）与量价运算框（输入预测生猪处理减少量，输出预测生猪价格）。

广义简约梯度法运算框（GRG box）：根据P-Y量价运算框输出的生猪出栏减少量（Y），结合分配函数（Φ）并设定相关约束条件，通过广义简约梯度法（GRG）输出最佳估计值：预测生猪出栏减少量的运算模型。

2 模型结构设计

2.1 分配函数的结构及计算

2.1.1 主因强度因子（S）分析与计算方法

强度因子主要是基于主因在一个区域发生后，在该区域的流行病学作用强度逻辑，即主因发生后影响持续M个月，每个月影响强度为βm(m=1,2,3,…,M)，总强度因子（S）如列式（1）：

主因作用产生后，受资金和复养信心等影响，一部分受主因作用而淘汰的产能在短时间无法复产，据此本模型将24个月内无法复产部分的强度因子记为S^sp，如列式（2）：

由列式（1）和列式（2）可得：

以受主因影响能繁母猪数（X）为自变量，通过强度因子（S）参数β可以计算能繁母猪减少数（Z），

计算模型如下：

其中xi表示自变量在第i个月上的值(i=0,1,2,…,N)，zt表示因变量在第t个月上的值(t=0,1,2,…,N+M-1)，主因强度影响持续M个月，故因变量可在最新自变量观测值基础上预测至未来M-1个月的值。

该计算公式的矩阵形式可表示为：

2.1.2 主因时间因子（T）分析与计算方法

⑴生猪生产技术指标计算方法

生猪生产具有一定周期性，这也导致主因对生产产能的减产影响在时间维度上具有周期性规律，因此生猪繁育周期、MSY等生产技术指标是计算主因时间因子（T）的关键一环。生猪繁育从母猪繁育到育肥猪出栏具有明显的阶段性，经历阶段不同所需的繁育周期常数也不同，如列式（7） （8）：

MSY指每年每头母猪出栏育肥数，本模型基于月度数据建立，故定义MSM为每月每头母猪出栏育肥数，用来衡量受主因减少的能繁母猪导致生猪出栏减少的效率，计算如列式（9） （10） （11） （12）：

⑵不同生产模式（C）下减产复产周期(tij)的计算方法

复养时间和生产模式的不同使得生猪减产复产时间产生变化，进而影响主因时间因子（T）的计算，记：

B2的情况已包含在强度因子列式（2）的计算中，故时间因子中不再重复考虑其影响，由列式（8） （13）（14）可得：

⑶主因时间因子（T）的计算方法

时间因子主要分析不同生产模式下受主因影响后生猪减产复产的时间逻辑，参数表征主因发生后，每头受主因影响减少的能繁母猪在未来一段时间内导致的生猪出栏减少量在每个月的分配情况。记：

根据列式（12） （17）建立Tc的计算模型如下：

其中参数γij表示第j种生产模式下 (j=1,2,3,4,5)，主因发生后第i个月 (i=0,1,2,…)的时间因子。当减产未开始 (iint(t2j))，时间因子不产生作用；当处于减产复产周期内时，时间因子表示每头受主因影响减少的能繁母猪导致的当月生猪出栏减少量（完整月份即为MSM，不足一月的按比例计算）。

由列式（15）和公式2-1可计算总时间因子（T）：

时间因子只考虑主因发生后24个月内可复产的情况，以可复产的能繁母猪减少数 (Znsp)为自变量，通过总时间因子（T）参数γi可以计算标猪出栏减少量（Y），计算模型如下：

其中ztnsp表示自变量在第t个月上的值 (t=0,1,2,…,N+M-1)，γi表示时间因子在第i个月上所有生产模式的总值 (i=0,1,2,…,L)，时间因子的作用时长（即i的最大值）取决于不同生产模式中最长减产结束时间 (L=MAX(int(t2j))，L≤24)。y_n表示因变量在第n个月上的值(n=0,1,2,…,+N+M+L-2)，主因时间影响最长持续L个月，故因变量可在最新自变量观测值基础上预测至未来L-1个月的值。

公式2-1、2-2、2-3的矩阵形式可表示为：

2.1.3 分配函数（Φ）计算方法

主因在某一区域发生后，在该区域流行持续M个月，在这M个月内，每个月不同强度的主因同时又作为独立的1起疫情以该月为起点对未来i个月的生猪出栏减少量造成影响。主因以上述方式构成了强度-时间双维度的作用矩阵 (φim)，由列式（1） （2） （3） （12）和公式2-2可得：

不可复产部分最长持续时间为B2≥24，可复产部分最长持续时间为L≤24，故φim的i值的最大值取B2。分配函数（Φ）为同一月份的合计影响值，需将矩阵（φim）转换为数据序列φt，表示自第1起主因发生后第t个月的分配函数值，计算如下：

以受主因影响能繁母猪数（X）为自变量，通过分配函数（Φ）参数φ_t可以计算标猪出栏减少量（Y），计算模型如下：

其中xi表示自变量在第i个月上的值 (i=0,1,2,…,N)，φt表示分配函数在第t个月上的值 (t=0,1,2,…,B2+M-1)。yn表示因变量在第n个月上的值 (n=0,1,2,…,N+B2+M-2)，分配函数 (Φ)最长分配时间为B2+M-1个月，故因变量可在最新自变量观测值基础上预测至未来B2+M-2个月的值。

公式3-1、3-2、3-3的矩阵形式可表示为：

2.2 量价运算框的结构及计算

在2.1章节分配函数的设计中，已建立主因发生后标猪出栏减少量（Y）在之后一段时间内每个月的分配规律模型。本章节的量价运算框则构建了标猪出栏减少量（Y）与生猪价格（P）之间的运算模型，按输入与输出变量不同，可分为P-Y量价运算框（输入实际生猪价格，输出生猪出栏减少量估计理论值）与量价运算框（输入预测生猪处理减少量，输出预测生猪价格）。

生猪价格需求函数Q=f(P)以及猪周期起点标准猪肉年供应量的变化函数Qt=f(i)是实现量价运算的重要函数：

2.3 广义简约梯度法（GRG）运算框结构及计算

根据分配函数Φ（公式3-3）构建规划求解的Y-X函数方程，采用广义简约梯度法（GRG）求自变量X变化情况下因变量Y的最优解，即得出预测标猪出栏减少量，使得P≥Pthr（Pthr为设定有效性筛选阈限值）条件下，GRG法计算出的最优解与2.2中由量价运算框计算出的理论值Y的相关系数最大，运算逻辑如图2：

2.4 价格预测技术路线及结果评估方法

量价运算框与GRG运算框是本模型价格预测技术路线的核心成分，以实际价格序列数据作为输入值，经过3步运算，可得到未来预测价格的序列数据。将输入的序列数据分为3个不相交的集合：

训练集：输入模型进行运算，获得训练误差；

验证集：与训练集相对独立，获得模型在该集上的预测误差；

测试集：与训练集和验证集相对独立，获得模型在该集上的测试误差。

本文采用3项拟合指标对模型预测结果进行评估，具体评估方案如表1：

2.5 预测结果迭代计算

本模型预测结果并不是静态值，而是进行迭代计算，即模型运算结果随输入的实际价格数据序列的更新而更新。这种迭代设计使本模型可以尽可能接受最新的价格波动信息，对历史预测进行纠偏。记：

3 模型测试及预测结果

3.1 样本数据与抽样说明

本轮猪周期受2018年8月国内暴发的非洲猪瘟疫情影响，故为验证本模型预测效果，本文选取2018年8月1日至2020年7月31日（不含节假日）的全国生猪均价日度数据作为原始数据总体（F），数据取自卓创资讯，见图4。从总体F中抽取每月的最高价形成月度数据样本（P，即当月生猪最高日均价）作为研究样本，记：

价格越高，则受主因影响导致的减产越严重，主因对价格波动的解释力就越强，而均价则会在一定程度上削弱主因的解释力，故本文研究样本的选择使用最高价而不是均价。

3.2 参数α与β的确定及分配函数计算结果

对多组α与β取值进行评估筛选，最终确定值为

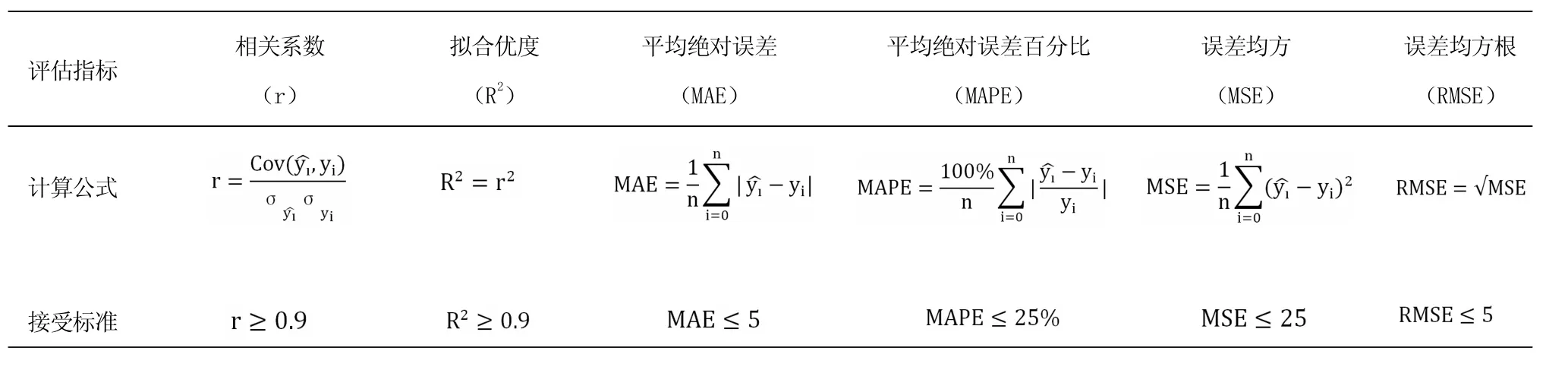
表1 预测评估指标及方法

生猪繁育周期常数及生产技术指标如下：

表2 生产技术指标

将上述参数代入公式3-3得出分配函数，分配函数曲线近似正偏态分布曲线，上升段短而快，下降段长而缓，如图5。

3.3 预测价格计算

依据生猪行业的历史数据及国家统计公布的人口数据，可得量价运算框涉及常数q＝75%，w＝110 kg，Pop＝14亿，同时对参数θ多组取值进行评估筛选，最终确定最优值θ＝2.5。公式4-1、4-2和4-3引用本团队另一研究结果：

将生猪价格样本数据（P）与上述参数值输入P-Y量价运算框，可计算出标猪出栏减少量（Y）。但是本模型是建立在主因导致产能减少进而影响价格波动的理论基础上的，忽略了影响价格波动的其他因素，如季节性需求变化和突发事件等。因此生猪价格（P）通过P-Y量价运算框计算出的每月标猪出栏减少量（Y），与本模型涉及的受主因影响的每月标猪出栏减少量之间存在偏差。当主因的解释力越强时，这种偏差就越小，本模型的预测性就越强，因此需要对Y进行有效性筛选，进而得出受主因影响的标猪减产量的最佳估计。

有效性筛选以生猪价格阈限为标准，假设P≥Pthr时，主因对价格波动的解释力最高，其他因素的影响几乎可以忽略不计。分析2006年6月至2018年7月3轮猪周期的价格波动，生猪价格的最高点都在20元/kg左右，而本轮猪周期生猪价格超过历史高位20元/kg，则假设Pthr=20。

将Y与有效性筛选阈值Pthr=20输入GRG运算框，参考国内能繁母猪存栏情况限定自变量X的取值范围为10≤X≤800（单位：万头），计算出Y的最佳估计。

为比较多次迭代结果变化，将不同时间更新的样本数据(Pi)输入模型，得出2019年12月（i＝16）至2020年7月（i＝23）共8次迭代计算的结果，如图7。

3.4 预测结果检验与评估

多次迭代计算结果在MAE、MAPE、MSE和RMSE指标上均达到检验标准，在训练集上计算的r和R2也均大于0.95，验证集由于受样本量限制（n＜8）没有表现出线性相关性，计算的r和R2参考性不大。见表3。

4 讨论

本模型试验测试过程使用的数据来源于卓创资讯，目前国内生猪价格统计数据来源众多，不同数据来源可以得到不同的预测结果，但只要原始数据统计标准一致就不影响模型趋势的预测。由于当前数据样本有限，模型测试时使用的训练集为全部样本数据，暂无其他数据集作为验证集与测试集进一步检验模型效果，因此由训练集计算出的评估指标值存在“过度拟合”的可能（即训练误差低估实际预测误差），无法完全表征本模型对未来价格的预测效果好坏。但是后期的模型迭代计算设计将弥补这一问题，使预测值随迭代更新。

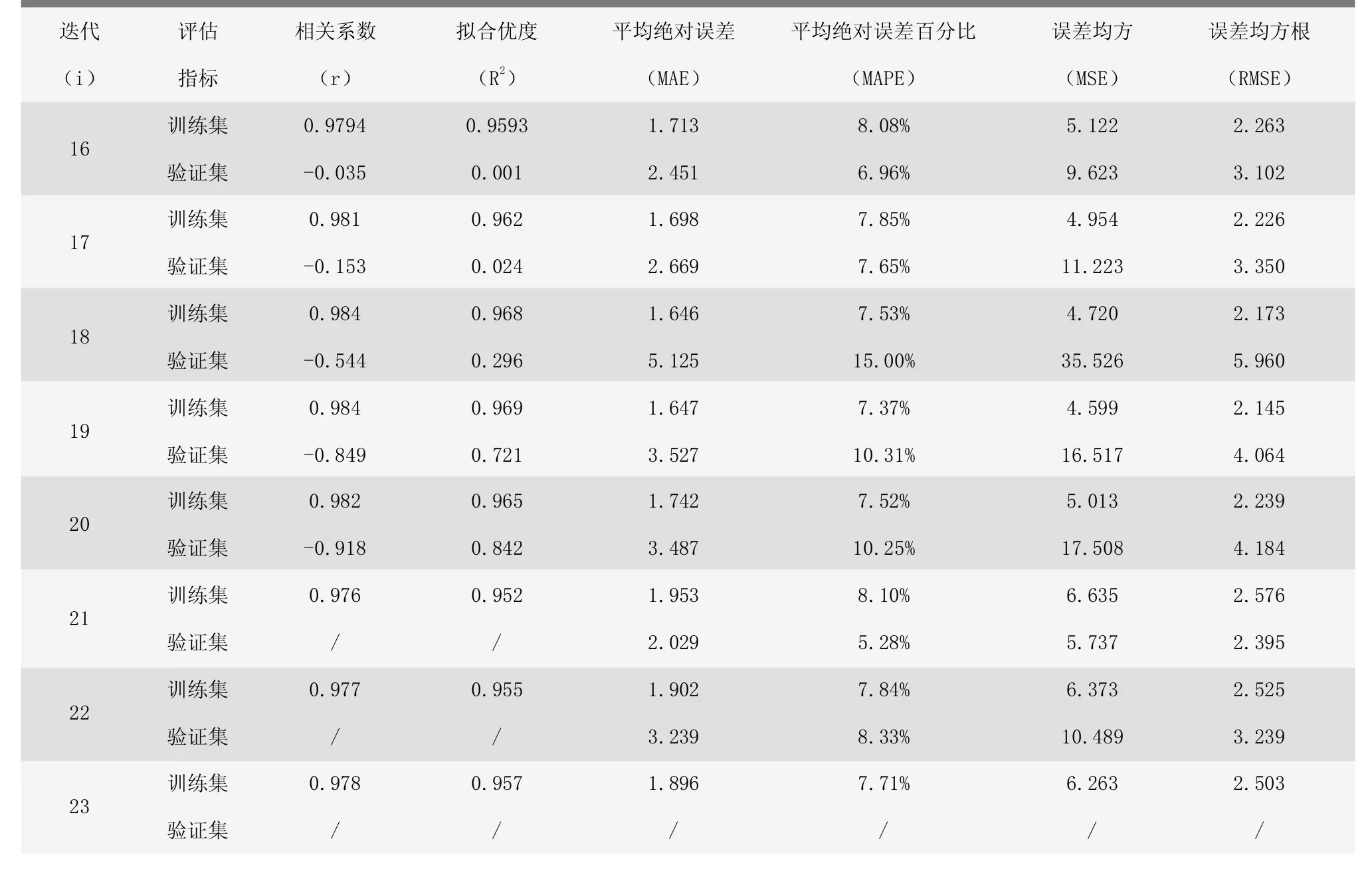
表3 预测结果检验与评估

本模型使用的参数α、β和θ取值的筛选过程，限于本文篇幅，不在此详细阐述，后续再对参数估计过程进行解释。

本模型量价运算框中应用需求函数及其反函数（公式4-1、4-2）的价格范围是12≤P≤40，当生猪价格超过这一数据范围时，会产生模型钝化。本轮猪周期实际预测过程中，超出定义范围的价格出现次数很少，因此不影响模型整体的预测效果。

本模型量价运算框在推导标猪数量对应猪肉产量时，标猪的体重（w）按110 kg计算，模型虽然最后通过2次量价运算框的计算（P-Y量价运算框与量价运算框）将这一因素抵消，从而不影响预测价格的趋势，但w会使预测价格的绝对值偏大或偏小。我们将继续研究价格与销售体重的最佳销售经济模型，以进一步消除预测误差。

本模型GRG运算框采用的有效性筛选阈值Pthr=20，该阈值的选择是存在决策误差的，但后期我们将根据数据量的增加，不断地校正这一因素，以减少决策误差。

本模型除主因影响外，只考虑宏观刚性需求的变化（公式4-3），未考虑季节性因素和突发性因素（如2020年新冠肺炎疫情）对猪肉消费的影响，因此预测价格对这2个因素产生的波动不敏感，当相关事件发生时预测值的绝对误差会偏大，但当这一事件结束时，模型将自行校正，因此不影响长期趋势的预测。如图7所示的多次迭代计算结果，受新冠肺炎疫情影响，2019年底至2020年初期间，虽然主因导致的减产因素仍然存在，但这一时期需求同时被抑制，导致生猪价格未能表现出主因的真实影响，主因影响被低估，于是预测价格出现整体偏低。随着新冠肺疫情得到控制，需求恢复，模型自动对前期预测进行校正，使得2020年7月迭代计算结果高于前期预测，因此本模型应用的预测价格通常采用最新迭代计算结果。我们后期将继续研究季节因素对需求的影响，以减少该因素产生的预测误差。

本模型只适用于分析本轮猪周期起因（非洲猪瘟）引起的减产因素对价格波动的影响，当非洲猪瘟因素结束或者生猪价格低于20元/kg时，本模型就不具备预测性，则需应用其他模型进行价格预测。