基于Scratch3.0实现迷宫生成与寻路程序
陈静
摘要:迷宫本质上是一个关于图的遍历算法的应用问题,即在给定的一张合理的迷宫地图上,找出正确的道路,走出迷宫。本文首先介绍生成随机迷宫的常见算法,其次介绍自动走迷宫的常见算法,最后介绍使用Scratch编程语言实现迷宫自动生成与走迷宫的核心程序。
关键词:Scratch;迷宫;算法
中图分类号:G642 文献标识码:A 文章编号:1007-9416(2020)09-0096-03
0 引言
迷宫可看做是一组连通图。对于生成迷宫,首先初始化所有的点都为墙,接下来需要做的就是在不重复访问的前提下遍历整个图中的所有点,在遍历图的过程中将相邻(指的是当前点的上下左右的邻接点)的两个点间的墙随机打通,也就是将当前点和邻接点都设置为路。生成迷宫的常见算法有:普利姆算法(Prim),深度优先算法(DFS),克鲁斯卡尔算法(Kruskal),广度优先算法(BFS)。这里以Prim和DFS为主介绍自动生成迷宫的步骤。对于走迷宫,最简单的思路就是依据图的搜索遍历算法对生成的迷宫地图进行遍历,寻找一条从起点到终点全是“路”的路线,常见的走迷宫算法有:左手法则、DFS、BFS。
1 生成随机迷宫
1.1 Prim算法
Prim算法本质是最小生成树,具体用Prim算法生成迷宫的步骤是:(1)初始化迷宫地图。即将地图中所有的点都设为墙;(2)任意选择迷宫地图中的一个点作为起点,将该点设置为路,以该点开始进行遍历,打通墙壁;(3)将起点周围(上下左右)是墙的点加入待处理墙队列中;(4)当待处理墙队列不为空时,进行循环,任选待处理墙队列中的一个点,将其设置为当前点;(5)判断当前点是否可以设置为路(依据是当前点的上下左右四个位置是否只有一个位置是路,也就是要保证迷宫路径没有环路且任意两条路径之间不交叉);(6)若当前点可以设置为路,首先将当前点设置为路,即打通墙壁,然后将当前点周围所有是墙的点加入到待处理墙队列中,接着从待处理墙队列中删除与当前点相等的点,若无法设置为路,直接从待处理墙队列中删除与当前点相等的点;(7)执行步骤(4),直至待处理墙队列为空。
1.2 DFS算法
DFS算法是一种“不撞南墙不回头”的算法。DFS算法的核心思路可简单概括为递归下去、回溯上来。顾名思义,递归下去是指以深度为基准,先一条路走到底,直至到达目标。若没有到达目标并且无路可走,那么返回到上一步的位置,走其他的路,这就是回溯上来。DFS算法采用递归回溯的方式,用到了数据结构栈,先进后出。使用DFS算法生成迷宫的具体步骤是:(1)首先初始化建立一个迷宫,此时要求所有的迷宫单元都是墙且是未访问状态;(2)随机选择一个迷宫单元作为起点,加入栈并标记为已访问;(3)当栈非空时,从栈顶取出一个迷宫单元(不用出栈)赋给当前迷宫单元,进行循环,循环的内容为:如果当前迷宫单元有未被访问过的相邻迷宫单元(上下左右),随机选择一个未访问的相邻迷宫单元,连通当前迷宫单元与相邻迷宫单元,标记相邻迷宫单元为已访问,并将其加入栈;若当前迷宫单元没有未访问的相邻迷宫单元,则栈顶的迷宫单元出栈;执行步骤(3),直至栈为空。
2 自动走迷宫
2.1 左手法则
左手法则是最简单、最易想到的走迷宫方法,该方法符合人的日常思维,对应的还有右手法则。都是针对有墙壁的迷宫,沿着墙壁走,最终都能走出去。左手(右手)法则只适用于小范围的固定迷宫,而大范围的迷宫虽然一定能找到出口但是很耗费时间。左手法则的具体思路是先走到左侧墙边;接下来每走一步都需要首先检测左侧是否有墙,如果有则直走,否则左转走到墙边;然后再检测前方是否有墙,如果有则右转,否则继续往前走,直到走出迷宫为止。
2.2 DFS算法
DFS算法實现走迷宫的思路与生成迷宫是一样的。具体步骤是:(1)对已生成的迷宫地图中的所有的迷宫单元设置为未访问状态,设置迷宫地图的起点和终点位置,将起点压入栈;(2)重复执行,直到当前单元的位置等于终点位置时结束循环,循环的内容为:1)获取栈顶元素(不出栈),将其赋值给当前单元,把当前单元所在迷宫位置标记为已访问状态;2)将当前单元周围情况(上下左右是“路”并且“未访问”的相邻单元)加入到待处理列表中,加入的顺序是“右-下-左-上”;3)若当前单元的待处理列表内容不为空,选取第一个,将其压入栈,否则栈顶元素出栈。
执行上述步骤后,栈内留下的元素就是从起点到终点能够连通的点。
2.3 BFS算法
BFS算法与DFS算法的区别在于:DFS旨在不管有多少条岔路,先一条路走到底,不成功就返回上一个路口,然后选择下一条岔路,而BFS旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,将它的分路情况记录下来,再返回来进入另外一个岔路,再把当前岔路的分路情况记录下来,重复这样的操作。BFS算法按照层次关系逐层遍历每个“路”结点,直至到达迷宫出口,借助数据结构队列,先进先出。BFS算法走迷宫的具体步骤是:(1)将起点压入队列;(2)重复以下步骤,直到队列为空。1)弹出队列第一个元素,将其设置为当前单元格,并将其标记为已访问;2)将其周围邻接节点(是路且未访问)压入队列;
为了确定从起点到终点的最佳路径,在循环过程中还需要将遍历过的节点和父节点分别存入到节点列表和父节点列表中。寻找最佳路径的做法是从终点开始查找它的父节点,将其存入最佳路径列表中,然后再找到父节点的父节点,再存放最佳路径列表中……,直至起点的父节点(假设起点的父节点为“-”,开始时将“-”加入到父节点列表)。
3 Scratch语言实现迷宫程序
以上两个部分分别介绍了生成迷宫与走迷宫的常见算法步骤,本节通过使用Scratch编程语言结合Prim算法实现生成迷宫,结合DFS算法实现走迷宫。
3.1 生成迷宮
(1)定义相关变量与列表。变量有行数、列数、迷宫格大小(初始化迷宫地图时涉及的变量),当前迷宫格(标识当前搜索到哪个迷宫格),周边格子(当前迷宫格的上下左右相邻迷宫格),迷宫格id(私有变量,对克隆出每个迷宫格进行标记)、起点(标识从哪个迷宫格开始),下标i(用于遍历列表)。定义的列表有迷宫地图状态列表(迷宫地图中每个迷宫格的状态,标明迷宫格(克隆体)是路还是墙,列表的序号对应克隆体的编号,1代表墙,0代表路,初始时默认都是墙,即1),待处理墙列表(将当前迷宫格的周边墙列表内容依次加入到该列表中),周边路列表(当前迷宫格周边是路的加入到列表中),周边墙列表(当前迷宫格周边是墙的加入到列表中)。
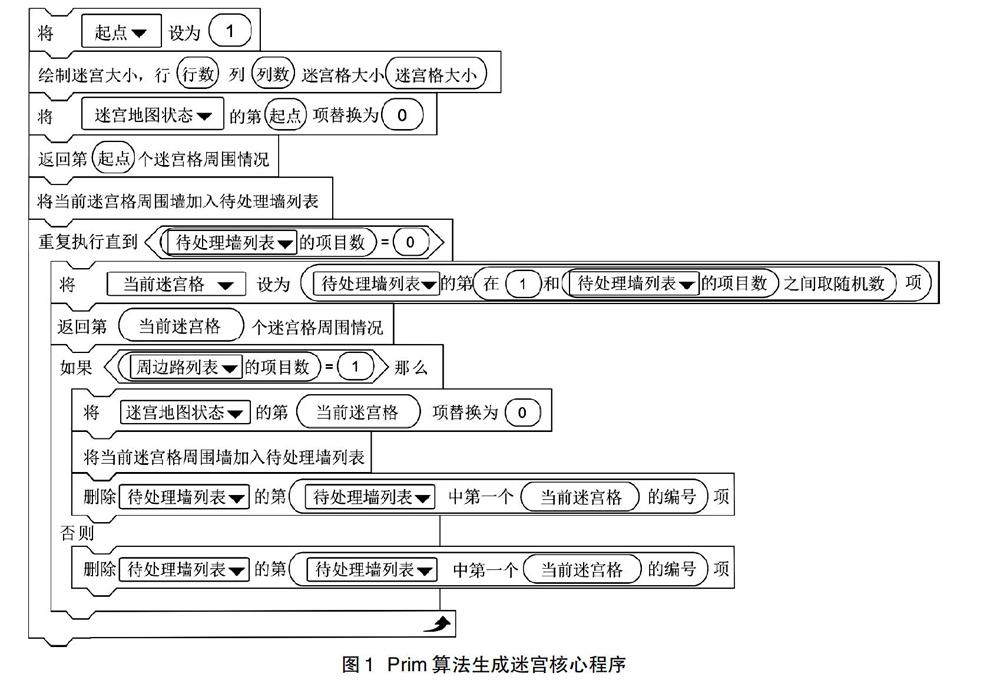
(2)依据Prim算法描述编写程序,其中“绘制迷宫大小,行列迷宫格大小”是初始化迷宫地图的函数。通过克隆绘制行乘以列个迷宫格,初始时每个迷宫格都是墙(即设置迷宫地图状态列表为1),最终由克隆体(根据迷宫格id区分每个克隆体)依据迷宫地图状态具体显示迷宫格是墙还是路,需要注意的是随着迷宫地图的生成,迷宫地图状态列表中的数据是不断变化的。“返回第X个迷宫格周围情况”是获取X迷宫格上下左右迷宫格的函数,X周边是墙的加入周边墙列表,是路加入周边路列表。“将当前迷宫格周围墙加入待处理墙列表”是指由“返回第X个迷宫格周围情况”函数得到的周边墙列表内容依次加入到待处理墙列表中。
假设左上角(第一个迷宫格)是起点,右下角(第行数乘以列数的迷宫格)是终点,将左上角和右下角的迷宫格设置为路。生成迷宫的核心程序如图1所示。
3.2 走迷宫
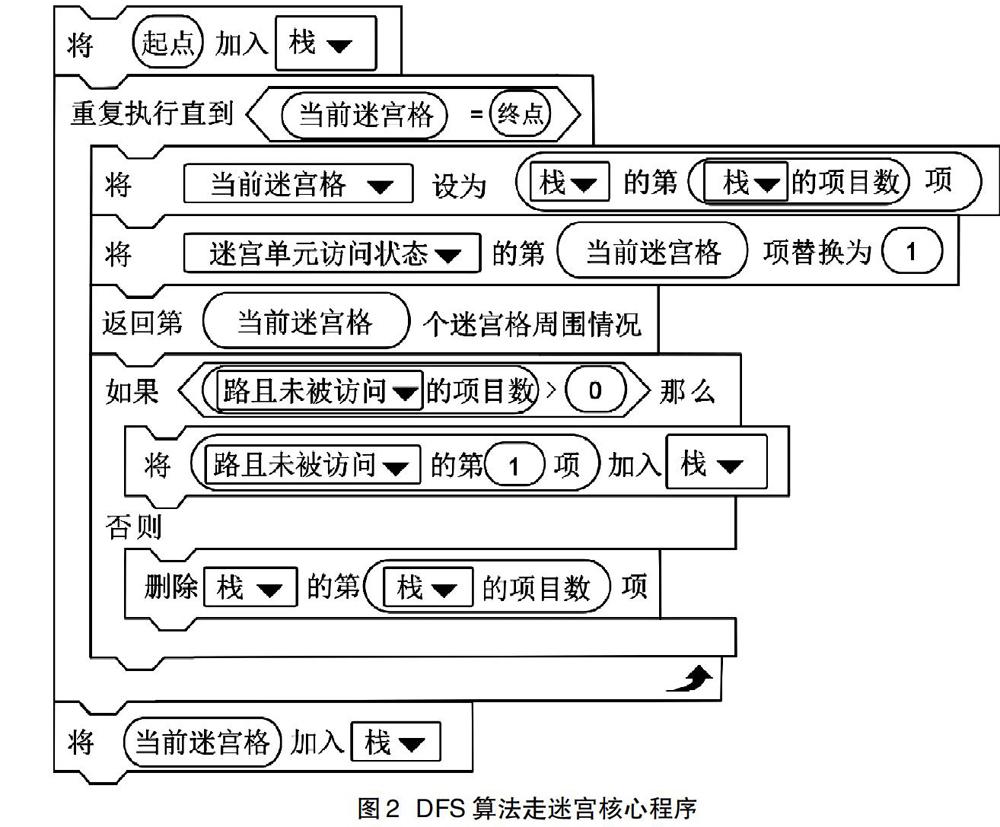
依据上述DFS算法描述编写程序,在上述变量基础上增加终点变量,路且未被访问列表(存储当前迷宫格右下左上是路且未访问的迷宫格),迷宫单元访问状态列表(初始时每个迷宫单元都为未访问状态,0表示未访问,1表示已访问),栈列表。走迷宫的核心程序如图2所示。
以上主要是借助最简单的图的搜索遍历算法实现迷宫程序,对于解决迷宫问题还应该从提高迷宫搜索效率和最优路径等方面考虑,如基于A*算法改进的向心法法则[1](将Dijkstra和BFS两种算法结合,兼顾速度与最优路径)、基于概率距离的算法[2](缩短迷宫搜索时间)。
参考文献
[1] 高源,凌翌,吕鹏.基于A*算法的迷宫搜索向心法法则[J].电子设计工程,2019,27(9):37-40.
[2] 王磊,董珊,潘洪友.基于概率距离的电脑鼠迷宫搜索算法[J].科技创新导报,2016,13(3):93-95.

