动态信息物理融合系统实时数据服务

邵亚丽，陈海华，张立臣，陈雪娟

(1.广东理工学院，广东 肇庆 526000；2.广东工业大学，广东 广州 510006)

0 引 言

CPS是涉及信息系统和物理系统交互与融合的一个崭新的研究领域，具有重大研究价值[1-2]。它具有复杂性、异构性、深度融合、自组织与自适应、实时性、海量性等特性，能为大型系统提供动态控制、信息服务和实时感知等功能[3-5]。其中实时性是CPS的重要特征，对CPS系统至关重要[6-10]。在这些系统中，每种操作模式的特征在于由不同的更新事务集执行的一组功能。称这种信息物理融合系统为动态信息物理融合系统(DCPS)[11]。如飞机控制系统，在该系统中，每个模式由不同的任务集组成，可以根据任务集区分着陆，起飞和正常巡航模式。目前国内外也有许多学者对CPS的实时性进行研究，文献[12]在提高实时任务的调度性能以及系统资源利用率方面提出了改进的调度算法，文献[13]对CPS中实时性控制任务提出一种改进的自适应调度策略，从而降低系统功耗，提高计算性能。文中从DCPS的数据管理层面研究了它的实时性方法，目标是在保持数据对象时间有效性的同时，保证在操作模式改变之前和之后还是模式改变的期间，都最小化数据的陈旧性。

1 任务和模式切换模型

为了能够在保证数据新鲜度的同时实现更低的数据陈旧度以及更好的更新事务可调度性，需要解决两个问题：(1)如何选择模式；(2)何时进行切换。针对问题1，在调度算法的选择上采用贪心策略；针对问题2，提出两种算法：分别为基于搜索的切换(SBS)和基于调整的切换(ABS)，当满足时间有效性约束时，来确定适当的切换点。SBS在模式改变请求(MCR)释放之后检查每个空闲时段的开始时隙并检验它是否是适当的切换点；ABS进一步放宽对可用切换点选择的限制，并调整MCR和当前时隙之间的调度。与SBS相比，ABS大大增加了可用切换点的数量，进一步提高了MCR的快速性[14]。

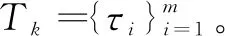
完成任务：是在旧模式下活动但不在新模式中出现的任务。在MCR之后没有新任务释放的情况下，允许它们在旧调度策略下完成。为了保证它们的时间有效性，不能中止它们。

新任务：是只出现在新模式中的任务。它们在适当的切换点同时释放。

未更改的任务：是经历模式切换的持久化任务。它们在MCR之后在旧的调度策略下被执行和释放，直到新的调度策略控制。应当仔细选择切换点，以在切换期间保持时间有效性。

已更改的任务：是在两种模式都出现但在新模式下有不同参数(如Ci和Vi)的任务。这些任务的时间有效性在切换期间还必须保持。

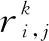
2 实时系统调度算法

文中主要考虑三个调度策略：HH，ML和DS-FP。DS-FP是这三个中可调度性最好的，但是具有最差的数据新鲜度，算法思想如下：

HH的基本思想是：为保持实时数据对象的有效性，在保证更新事务τi的周期和相对截止时间之和不大于该事务的有效时间间隔长度的前提下，规定τi的周期等于其相对截止时间，且都等于有效期间隔的一半[2，5，10]，即Pi=Di=Vi/2。

ML的基本思想是：采用周期性事务模型，在保证更新周期和相对截止时间的和不大于更新数据对象的有效期间隔的前提下，设置更新事务的周期Pi大于相应更新数据的有效期间隔的一半，即Pi+Di≤Vi,Di≤Vi/2≤Pi。

ML的提出是为了最小化更新工作负载，它使用单调截止时间(deadline monotonic，DM)[3]来调度周期性更新事务。

DS-FP的基本思想是[5]：以非周期性硬实时事务模型为基础，在确保实时数据对象更新时间有效性的同时，尽可能推迟当前更新事务作业Ji,j的后继作业的释放时间ri,j+1，从而增加同一事务两个连续作业的时间间隔，以降低CPU的工作负载[4-5,14]。其动态地为更新事务的作业分配周期和相对截止时间。

根据更新事务产生的工作负载来选择调度策略(UBSS)，如图1所示。当用MCR通知系统时，它将分别计算HH和ML下的新任务集的周期和截止时间。如果任务集在HH下不可调度，则将尝试使用ML。当HH和ML都不能用时，将仅采用DS-FP。如果任务集甚至不能通过DS-FP的可调度性测试[8]，系统将报告错误，因为到目前为止，没有比DS-FP能更有效地保持实时数据对象的时间有效性的调度算法。

图1 基于利用率的调度策略选择

因为在调度切换期间可能改变未改变任务的时间有效性。因此即使旧的和新的任务集在所选择的调度策略下是可调度的，也不能保证将保持实时数据的时间有效性。因此，为了满足所有事务的时间有效性约束，应当仔细选择切换点。在此提出两种算法来搜索适当的切换点。以下是两个搜索算法的伪代码，如图2和图3所示。

算法1：基于搜索的切换算法

输入：Tk,Tk+1,ψk,ψk+1,开始搜索时间t0及tL

输出：tw

1：fort=t0tot0+tLdo

2： ift==t1then//t1为空闲时间段的开始点

3：f=TRUE;

4： //判断t是否能选为tw

5： for eachτi∈Tk∩Tk+1do

6：ts=ψk中τi的最后作业的释放时间；

7：l=ψk+1中τi的第一个作业地完成时间；

8： ift-ts+1>Vithen

9：f=FALSE;

10： end if

11： end for

12： iff==TRUE then

13： returnt;

14： end if

15： end if

16：end for

17：returntw不存在；

图2 SBS算法

算法2：基于调整的切换算法

输入：Tk,Tk+1,ψk,ψk+1,t0及tL

输出：tw

1：fort=t0tot0+tLdo

4： continue；

5： else //调整[t0,t)间Tk的调度

6：f=ScheduleAdjustment(Tk,t0,t);

7： iff=FAIL then

8： continue；

9： else

10： for eachτi∈Tk∩Tk+1do

11；ts=ψk中τi的调整请求时间；

12：l=ψk+1中τi的第一个作业的完成时长；

13： ift-ts+l>Vithen //违反时间有效性

14：f=FAIL;

15: end if

16: end for

17: iff=SUCCESS then

18: returnt;

19: end if

20: end if

21: end if

22： end for;

图3 ABS算法

3 仿真结果

文中实验都是利用MATLAB下的simulink工具实现的。表1为实验参数设置。

表1 实验参数设置

(1)UBSS与ML、DS-FP的调度成功率、CPU利用率的仿真对比。

在本实验中，模拟系统中有10个连续模式，每个模式固定持续20 000个时间单位。每种模式的密度系数如图4(a)所示。在每个模式中随机生成200个任务集，实验主要研究CPU利用率、调度成功率、数据陈旧性、调度开销和切换延迟。

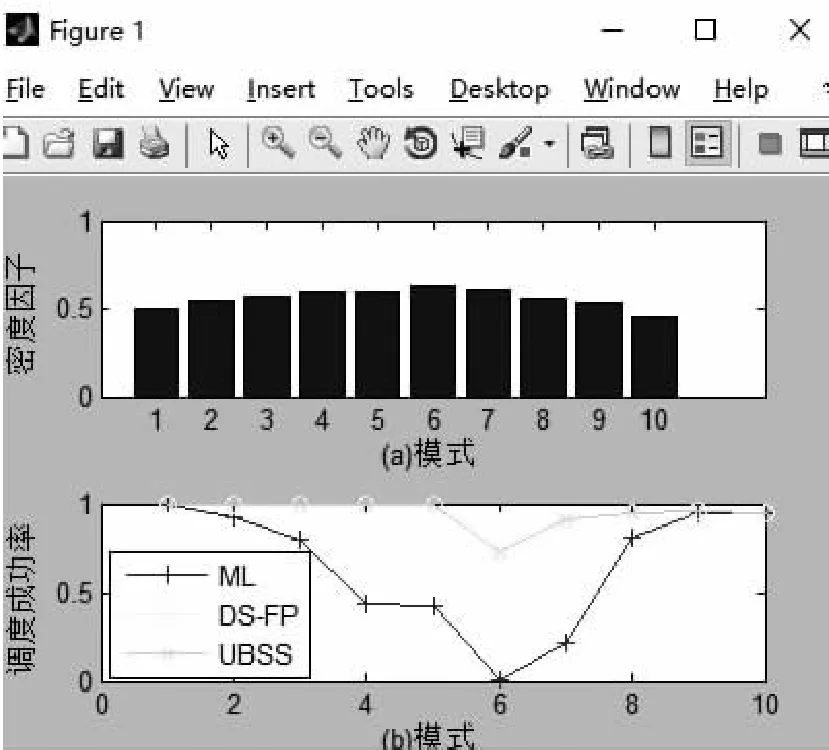
图4 调度成功率和密度因子

图4(b)给出了ML，DS-FP和UBSS的调度成功率的结果。从图中可以发现，DS-FP和UBSS在具有不同密度因子的不同模式中总是具有相同的成功率。这是因为在每个模式的开始，UBSS将进行可调度性测试，并选择最适合的调度策略。如果任务集仅在DS-FP下可调度，则UBSS将为了最大化可调度性而选择DS-FP。此外，还能发现这三种方法的成功率都随着密度因子的增加而下降，但DS-FP和UBSS始终优于ML。当密度因子为0.63时，ML的成功率低至0.01，而DS-FP和UBSS的成功率仍然可以保持在0.79。当密度因子低于0.55时，这三种方法都具有相同的成功率，因为这时所有任务集都可由ML调度。

图5显示了三种方法中CPU利用率的比较。如前所述，与ML相比DS-FP可以极大地降低CPU的利用率，同时仍然保持时间有效性。其中DS-FP的CPU利用率始终低于ML，并且当模式6中的密度因子为0.63时，差异达到15.1%。而UBSS的CPU利用率在ML和DS-FP之间。当密度因子低时，UBSS的CPU利用率接近ML，因为大多数任务集此时可以在ML下调度，并且为了维持更高的数据新鲜度和更低的在线调度开销UBSS优先选择周期性调度策略。另一方面，当系统工作负载较高且大部分任务集仅在DS-FP下可调度时，UBSS选择DS-FP以最大化可调度性,此时它的CPU利用率将接近相应的DS-FP调度。

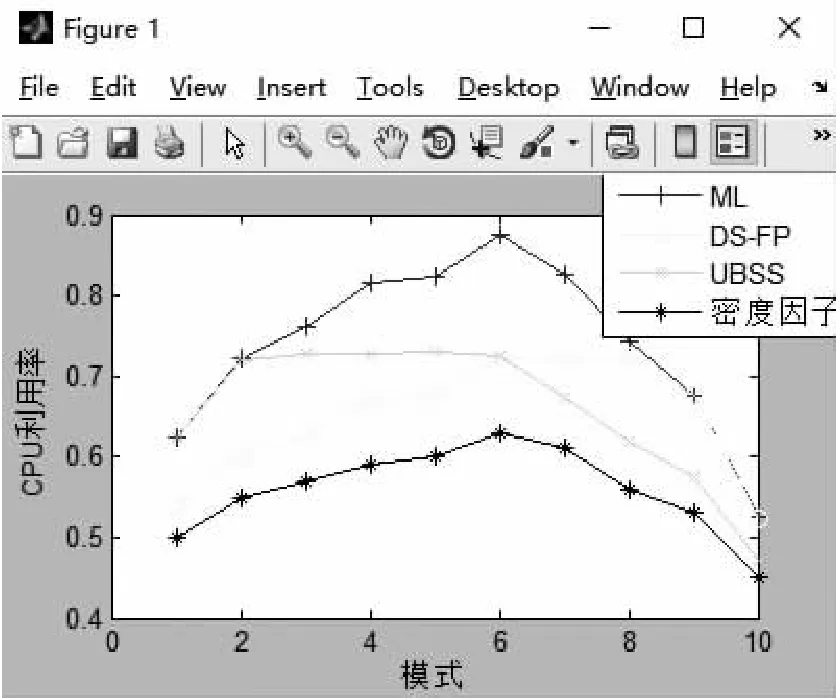
图5 CPU利用率比较

(2)UBSS与DS-FP在数据陈旧度的仿真对比。

图6 模式数据陈旧度和CPU负载

(3)ABS和SBS的仿真对比。

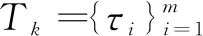
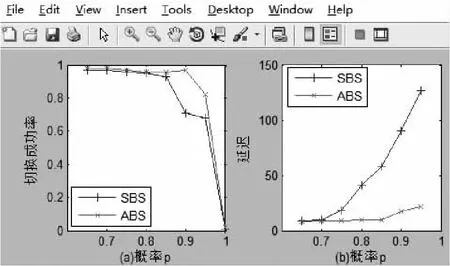
图7 ABS和SBS成功率和延迟仿真结果

由图7(a)可以发现，当概率p增大时，SBS和ABS下的切换成功率都下降。这是因为Tk+1的事务越多，可选切换点上的时间有效性约束越多。另外，通过调度调整主动创建切换点，而非被动搜索，ABS总是在切换成功率方面优于SBS，当百分比p提升到95%时，它们的差值达到14%。由于Tk在ML下不可调度，当p=100%时，Tk+1等于Tk，并且它们的成功率都降为0。图7(b)显示了SBS和ABS之间的切换延迟的比较。可得，ABS相比SBS总是具有较低的切换延迟，并且当p增大时，它们的差值增加。这是因为SBS限制仅在空闲时段的开始时隙选择切换点，而ABS没有该约束。通过合理的调整，ABS极大地增加了调度切换候选的数量，并潜在地提高了切换延迟。

4 结束语

主要研究了如何在动态信息物理融合系统中，在模式变化的情况下保持实时数据的时间有效性的问题。介绍了任务和模式切换模型，研究了在线调度切换问题，建议在不同的模式下使用不同的调度策略，并引入两种算法来搜索适当的切换点。最后通过仿真模拟论证了算法的有效性。