适用于分散式电网中无功功率最优调度的控制算法研究

谭昱霖 李磊

摘要：为了降低微电网系统发电过程中的系统损耗，提高功率传输效率。本文对各种无功系统调度目标进行了讨论，采用了粒子群算法求解最优无功功率调度方案，并采用IEEE电网模型进行了仿真。仿真结果表明，采用此算法可以在有效时间内得到收敛的优化调度方案，为有效降低发电成本提供了参考意见。

关键词：微电网；无功调度；粒子群算法

能源是现代社会和经济发展的动力，随着化石能源的枯竭与对环境的破坏效应，能源行业重心逐渐偏向于可再生资源利用与环境保护可持续发展的新能源。随之伴生的便是微电网这种新型网络结构的产生和发展。微电网可以对一定范围内的分布式电源进行网络化的综合管理，实现能源利用的合理分配。

清洁可持续再生能源的大规模利用正在研究解决2个方面的重大科学技术问题：其一是低密度能量的大规模高效率的转换为电能的技术，我国多部委也多次立项支持其研究；其二是分散的、随机的电能量的安全传输与可靠使用，国内对风能发电接入电力系统后带来的运行控制问题研究已经有多年的历史[1]。

无功功率是交流系统中的一种具有重要用途的现象。由于电网主要阻抗大都是无功阻抗，有功功率输电在各个节点之间存在一个电压相角差，同时无功功率输电需要在多个节点之间选择合适的电压差。因此，选择合适的无功输电有助于提高局部输电线路的效率，减小有功损耗。

1.最优无功功率调度目标

最优无功功率调度通常被视作为最优潮流的一部分，通常来说，在多个节点的电源模型中，最优潮流设计为最小化有功功率损耗，也可以根据生产实际需要选择其它模式，典型的目标函数如下。

（1）有功功率损耗最小化

有功功率损耗（Ploss）最小化的目标函数公式为

式中，Vi，δi分别为节点i的电压幅值和相角，gk为节点间输电线路k的电导率，n为节点的个数。

（2）电压偏差最小化

电压偏差最小化目标函数定义为

式中Vk为节点k的电压幅值，Vk为节点k的目标电压幅值，n为节点的个数。

（3）多目标函数

最小化的目标函数可以根据生产需要，有复数个单目标函数与权重因子的组合得到。多目标函数公式如下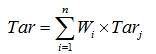

式中Wi为目标函数的权重因子，Tari为目标函数i，n为考虑问题中目标函数的个数。

2.约束条件

在无功功率调度过程中，约束条件分为两个部分，其中一部分是有功潮流与无功潮流平衡，另一部分则是系统的极限能力。

（1）潮流方程

4.算例分析

在一個具有10个电源节点和35个消纳节点的系统上测试配置的算法，将测试目标简单设定为求电网全局有功最大化，对该问题执行复数次以观察该算法的性能可以得到如图1所示的收敛特性，根据收敛特性可知，这个算法可以在较快的迭代次数内即得到收敛的结果，也即是在对设备的算力没有特殊要求。

5.结语

本文所提供的一种算法可以在算力有限的情况下，快速求解节点不甚多的多节点电力系统无功功率调度最优解的方案。根据该算法对算例的收敛特性分析，其结果表明本文方法具有较高的可行性。

参考文献

[1] Q/GDW- 2012.分散式风电接入电网技术规定.北京：中国电力科学研究院新能源研究所.2012

[2]W.ongsakul and P.Jirapong，”Calculation of total transfer capability by evolutionary program m ing，”In proceedings of IEEE Region 10 Conference（TENCON2004），pp.492-495，2004