1T2R三自由度海浪发电装置设计及运动学分析

赵裕明，金振林，2*，冯海兵

(1.燕山大学 机械工程学院，河北 秦皇岛 066004；2.河北省重型智能制造装备技术创新中心，河北 秦皇岛 066004)

1 引 言

海洋波浪能是清洁的、无污染的可再生能源，有效利用波浪能量对缓解能源危机、减轻环境污染具有重要的作用和意义。自1974年Salter提出了点头鸭波能转换装置后[1]，世界各国相继开始了海浪发电技术的探索与研究。海浪发电技术按照工作原理主要分为振荡水柱式、振荡浮体式和越浪式等形式[2-4]。近年来振荡浮体式海浪发电技术的研究较多，其原理是利用浮体与机架的相对运动，将波浪能转换为机械能进而做功发电。最为典型的是英国的Pelamis波能装置、Oyster波能转换装置和美国的PowerBuoy装置[5-7]，这些装置已经开始商业化运行。现有的振荡浮体式海浪发电装置绝大多数为单自由度机构[1，3，6-7]，能量转化效率并不理想。海面自由浮体能够实现六维运动，主要是垂荡与摇摆运动，如果海浪发电装置的浮子能够吸收采集三维运动的动能与势能，必将提高装置的能量采集与转换效率。Chen Weixing、马春翔等将并联机构作为海浪发电装置的波浪能量采集转换装置[8-10]，目前这类研究较少。

本文提出了一种能够实现一维移动和二维转动含有冗余支链的三自由度并联机构，基于该机构设计了一种海浪发电装置的波浪能量转换装置，采集波浪能的浮子与机构的动平台固接，浮子在波浪力作用下的垂荡和摇摆运动即机构动平台的一移两转运动。相对并联机构而言，波浪力即为并联机构的驱动力，3条RUS支链被动受力为末端执行器，中间布置的平面四杆机构不仅作为约束分支，同时也作为末端执行器承受载荷，这时该机构便成为含有冗余支链的三自由度并联机构。相比于六自由度能量转换机构，本文所研究的机构能有效避免浮子随波推移不易复位的问题。此外，3条RUS支链的球副均布在动平台圆周边缘，使浮子受力均匀，冗余支链在限制浮子运动的同时承担部分波浪力，提高了装置的发电能力。本文首先介绍了海浪发电装置的原理以及波浪能量转换装置的原型机构，之后依次对浮子运动学、并联机构运动学、装置工作空间、运动学性能指标进行了分析，该研究为装置的动力学分析、结构尺度优化及样机研制提供了理论基础。

2 波浪能量转换装置

图1所示的海洋波浪能量转换装置(以下简称为波能转换装置)为海浪发电设备的核心部分，作用是吸收和采集波浪能量，并将其转化为机械能，为后续的机械能转化为电能做准备。波能转换装置安装固定在海洋平台上，海洋平台可以悬停于海面上，也可与海底固接。波能转换装置主要由运动浮子、能量转换机构、运动转换装置组成。运动浮子漂浮在海面上，随着波浪一起运动，充分吸收波浪能量；能量转换机构将浮子的动能和势能转换为支链末端连杆的摆动；运动转换装置将机构支链末端连杆的摆动转换成整周回转运动，带动液压缸往复运动并产生高压油液，进而驱动液压马达并带动发电机组运转，液压管路上设有蓄能器用来稳定液压系统的压力。

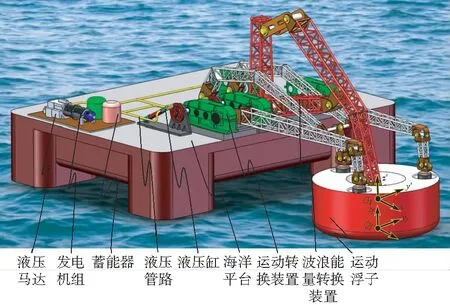
图1 海浪发电装置虚拟样机Fig.1 Virtual prototype of the wave power generating device

波能转换装置的原型为并联机构，由平面四杆机构和3-RUS机构两部分组成，如图2所示。

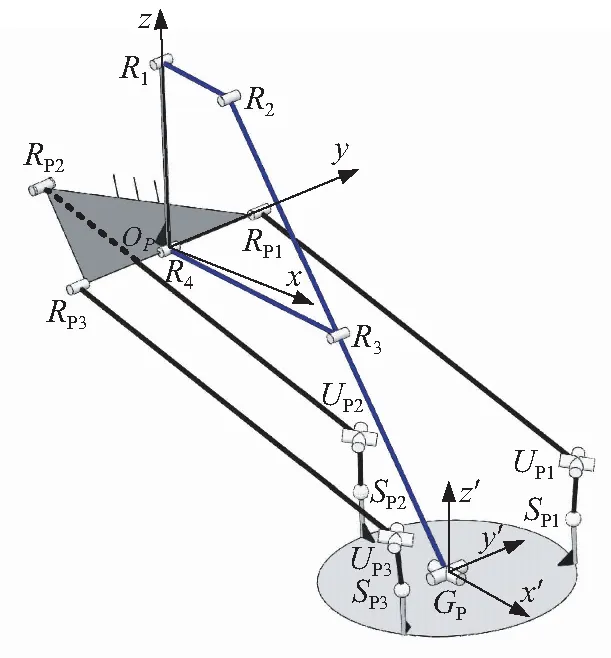
图2 波能转换装置机构简图Fig.2 Schematic diagram of mechanism of device

其中，3-RUS机构中的RUS支链一端通过转动副RPi与固定平台相连，另一端通过球副SPi与动平台相连，两个活动杆件通过虎克铰UPi相连。3个转动副RPi均布于固定平台等边三角形的3个顶点上，3个球副SPi通过立柱APiSPi与动平台固接，立柱APiSPi垂直于动平台AP1AP2AP3，APi均布于以GP为圆心的圆周上；平面四杆机构中转动副R1，R4固定在机架上，转动副R4与RP1和RP3同轴，转动副R1，R4，RP1，RP3同在一竖直平面内，连杆R2R3的延长线R3GP通过虎克铰与动平台中心GP点相连，四杆机构所有转动副轴线相互平行。平面四杆机构限制动平台中心点GP只能在平面内做二维移动，其中竖直方向为主运动，水平方向为伴随运动，同时动平台具有绕中心点GP处虎克铰两正交且水平的轴线转动，故机构具有两转一移3个独立自由度。由于机构含有3条RUS支链，为含有冗余支链的并联机构。

3 浮子运动学分析

浮子运动学是波能装置浮子设计的基础[11]。建立空间定坐标系Qf-xfyfzf，Qfxfyf面与静水平面重合，zf轴过初始状态的浮子中心竖直向上，xf指向波浪传播方向；动坐标系GP-x′y′z′建立在浮子质心GP点，z′轴垂直于浮子上表面方向向上，x′轴与AP2GP重合，如图1和图2所示。

浮子运动的角位移用欧拉角表示，坐标系GP-x′y′z′相对于Qf-xfyfzf的转角为γ，β，α，γ为横摇运动转角，即绕xf轴的转角，β为纵摇运动转角，即绕yf轴的转角，α为首摇运动转角，即绕zf轴的转角，则坐标系Qf-xfyfzf与坐标系GP-x′y′z′的关系为：

(1)

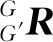
波浪扰动力由弗劳德-克雷洛夫力和绕射力两部分组成，可表示为：

(2)

某一时刻海浪传播方向是固定的，浮子的瞬时运动为垂荡与纵摇运动，垂荡运动即浮子沿zf轴的上下移动，其耦合运动方程为：

(3)

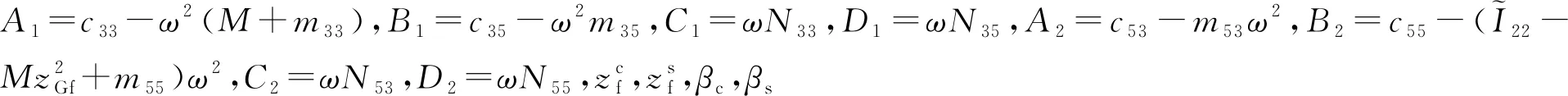
求解式(3)可得浮子运动轨迹为：

(4)

一个波周范围内浮子运动总功率为：

(5)

波浪功率为宽度Bw的波浪能沿波长方向所传送能流，表示为：

(6)

其中：cwg为群速，深水中cwg=cw/2，浅水中cwg=cw。

则波能转换装置浮子的能量采集效率为：

(7)

式(5)与式(6)中只含有波高Hw的二次项，故能量采集效率ηf的值与波高Hw无关。

设定3种浮子的形状分别为竖直圆柱体、上下表面为正方形的长方体及球体。设竖直圆柱体浮子圆截面直径为Df，3种浮子均有一半浸没在海水中，浮子材料、高度、静水平面截面积和吃水深度均相等，静水中圆柱体与长方体的排水体积和质量相等，具体参数见表1。

表1 3种浮子的主要参数

结合我国海域的实际情况[12]，在分析浮子形状对能量采集效率影响时，取波浪周期T为4～7 s，海浪波高为2 m，综合考虑浮子的加工制造、安装、维护问题，以及海浪发电装置的发电能力等因素，令圆柱形浮子直径Df的取值范围为2～12 m。在对比分析3种浮子能量采集效率时，以波浪周期和浮子中间水平截面尺寸为变量，绘制能量采集效率图谱，进而分析浮子形状和尺度对能量采集效率的影响。

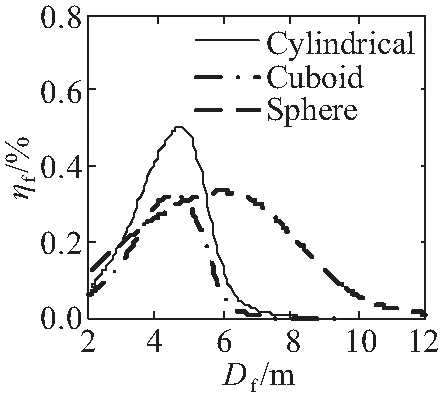
(a)T=4 s

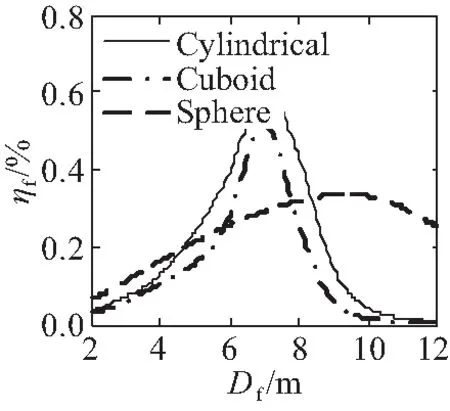
(b)T=5 s

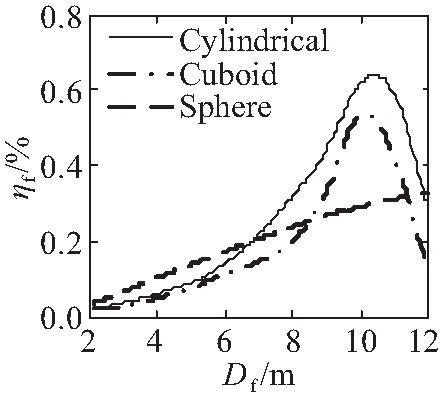
(c)T=6 s

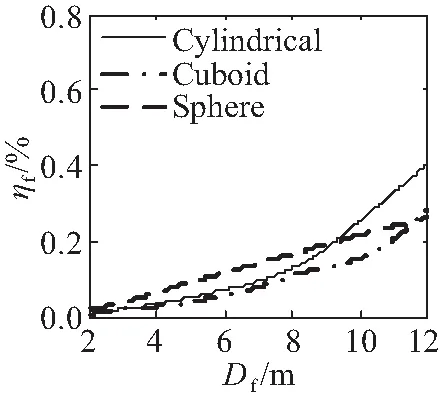
(d)T=7 s图3 浮子尺寸与能量采集效率的关系Fig.3 Relationship between floater size and efficiency of energy collection

从图3可以看出，圆柱体浮子的波浪能量采集效率始终比长方体浮子高；当浮子尺寸Df确定时，周期T在4～7 s间变化，圆柱体和长方体浮子的能量采集效率变动较大，球体浮子效率变化相对较小；圆柱体浮子适用于波浪周期变化较小的海域，球形浮子适用于波浪周期频繁变化的海域。

4 波能转换装置运动学分析

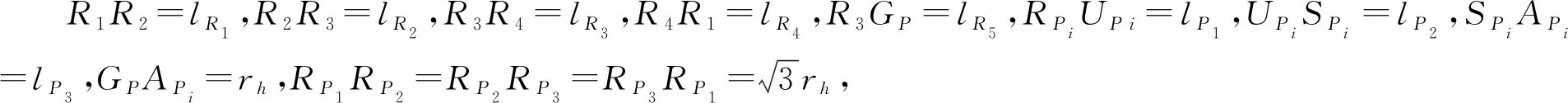
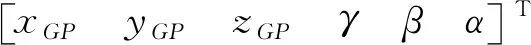
4.1 波能转换装置位置分析

平面四杆机构决定动平台中心GP点只能在xOPz平面内移动，由于海面上漂浮的浮子具有沿竖直方向的垂荡运动和绕两正交水平轴的摇摆运动，故设计平面四杆机构时，期望GP点在xOPz平面内只沿z轴竖直运动，无x方向的水平运动或相对运动较小。

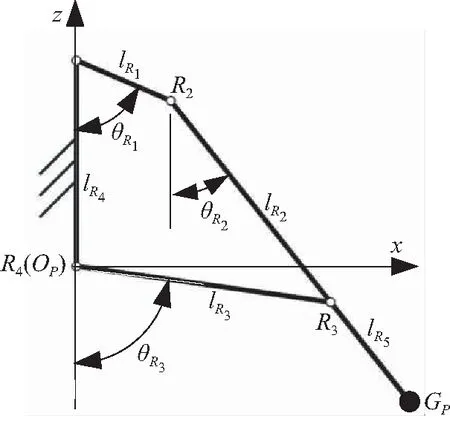
图4 平面四杆机构简图Fig.4 Schematic diagram of four-bar mechanism in planar

θRi(i=1，2，3)为R1R2杆、R2R3杆、R4R3杆与z轴负方向所成的角度，如图4所示，矢量方程为：

R1R2+R2R3-R4R3-R1R4=0，

(8)

其中：R1R2，R2R3，R4R3，R1R4分别为R1R2杆、R2R3杆、R4R3杆、R1R4杆的矢量。

将式(8)展开整理得：

(9)

解方程得四杆机构R2处转动副转角为：

(10)

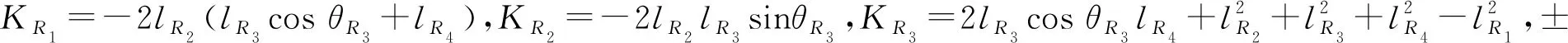
坐标系OP-xyz中GP点的矢量闭环方程为：

rGP=OPR3+R3GP=lR3nR3+lR5nR5，

(11)

其中：nR3=[sinθR3，0，-cosθR3]T，nR5=[sinθR2，0，-cosθR2]T，OPR3为R4R3杆的矢量，nR3为其单位矢量；R3GP为R3GP杆矢量，nR5为其单位矢量。

将式(11)展开整理得动平台中心GP点的位置为：

(12)

联立式(12)建立动平台的平动伴随关系为：

(13)

设计四杆机构使动平台中心GP点沿z轴做垂荡运动，而沿x轴的伴随运动数值越小越好。平面四杆机构几何参数为lR1，lR2，lR3，lR4，lR5，结合式(10)和式(12)的GP点轨迹数学模型，借助MATLAB根据期望的末端轨迹进行四杆机构尺度设计，最终确定各杆件的尺度关系为：

lR1∶lR2∶lR3∶lR4∶lR5=1∶2.5∶2.5∶2∶2.5.

(14)

通过分析可知，满足式(14)的尺度比例且当lR1=1时，动平台GP点沿z轴在[-2.2，1.7]范围内运动时，x方向最大波动量在0.009以内，完全能够满足波浪能量转换装置的工况要求。式(10)和式(12)即为平面四杆机构位置正反解。

3-RUS机构的位置分析即确定动平台位姿zGP，β，γ与各支链连架杆RPiUPi转角位置间的关系。

固定平台上RPi点在定坐标系OP-xyz中的位置矢量RPi可以表示为：

RPi=[rh(cosφPi-cos 60°)，rhsinφPi，0]T，

(15)

其中φPi=(2i-1)π/3.

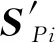
(16)

杆件SPiGP在定坐标系OP-xyz中的位置矢量rSGi展开表示为：

(17)

构造矢量闭环方程：

(18)

其中：nPi=[cosθPi，0，sinθPi]T，RPiUPi为RPiUPi杆的矢量，nPi为其单位矢量，θPi为杆件RPiUPi轴线与x轴正方向所成的角度；UPiSPi为UPiSPi杆的矢量，wPi为其单位矢量。

将式(18)中lP2wPi移到等号一端并对等式两端同时取范数得：

(19)

将式(15)～式(17)代入式(19)得到3-RUS机构连架杆RPiUPi的转角θPi(i=1，2，3)为：

(20)

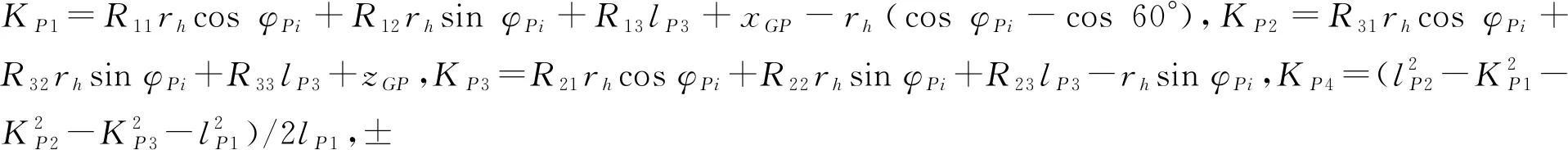
4.2 波能转换装置速度分析

式(11)各项分别对时间求导得：

(21)

vh=[vhx，vhy，vhz]T，

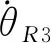
将式(21)展开表示为：

(22)

联立式(9)的方程组消去θR1后，各项分别对时间求导并整理得：

(23)

TR23=(-lR2lR3cosθR2sinθR3+lR3lR4sinθR3+
lR2lR3sinθR2cosθR3)/(lR2lR3sinθR2cosθR3-
lR2lR3cosθR2sinθR3+lR2lR4sinθR2).

将式(23)代入式(22)得平面四杆机构的速度映射关系为：

(24)

其中：Tvhx=1/(lR3cosθR3+TR23lR5cosθR2)，Tvhz=1/(lR3sinθR3+TR23lR5sinθR2).

联立式(24)得动平台线速度伴随关系为：

(25)

球副Si点的速度vSPi可表示为：

vSPi=vh+ωh×rSGi，

(26)

其中ωh为动平台的角速度。

将式(26)表示成矩阵形式为：

(27)

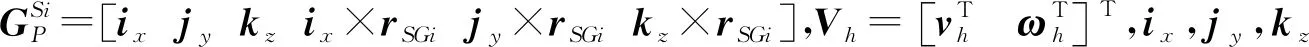
式(18)中各项对时间求导得：

(28)

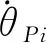
式(28)各项同时点乘wPi化简整理得：

(29)

将式(26)代入式(29)得：

(30)

结合式(24)与式(30)，将波能转换装置机构支链端速度与动平台位姿速度的映射关系统一写成矩阵形式为：

(31)

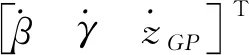
(32)

由式(31)和式(32)得到波能转换装置机构的速度映射关系为：

(33)

Jh=JhtJhu，

其中：Jh表示波能转换装置机构的速度雅克比矩阵，Jh∈R4×3。

4.3 波能转换装置加速度分析

式(22)各项分别对时间求导得：

(34)

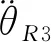
式(23)中各项分别对时间求导整理得：

(35)

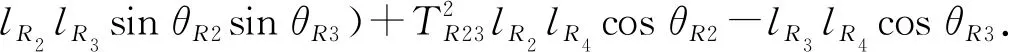
将式(23)、式(24)和式(35)代入式(34)整理得动平台线加速度与R4R3杆的角加速度关系为：

(36)

式(30)各项分别对时间求导得：

(37)

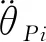
式(27)两端分别对时间求导得：

(38)

又有矢量UPiSPi可表示为：

lP2wPi=SPi-(RPi+lP1nPi).

(39)

式(39)各项对时间求导整理得：

(40)

将式(27)、式(30)、式(38)和式(40)代入式(37)整理得：

(41)

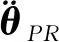
(42)

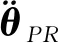
(43)

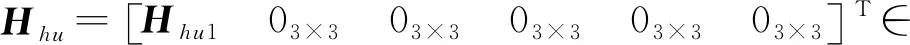
其中：Hhu1∈R3×3，Hhu1中第3行第3列的元素(Hhu1)3，3=TAhx-(TvhzTAhz)/Tvhx，其余元素均为0。

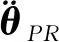
5 运动学仿真

设波能转换装置机构主要结构参数为：lR1=2 m，lR2=5 m，lR3=5 m，lR4=4 m，lR5=5 m，lP1=9.5 m，lP2=1.4 m，lP3=1.5 m，rh=2.5 m。设动平台的运动轨迹为：

(44)

借助MATLAB编程，得到机构支链末端的理论角位移、理论角速度和理论角加速度，如图5(a)～5(c)所示；利用软件ADAMS对机构进行运动学仿真，得到机构的机构支链末端的仿真角位移、仿真角速度和仿真角加速度，如图5(d)～5(f)所示。

通过对比图5(a)～5(c)与图5(d)～5(f)可知，MATLAB理论计算曲线与ADAMS模型仿真曲线完全一致，验证了机构运动学推导的正确性；另外，机构速度、加速度曲线变化连续、平滑，动力学性能较好。

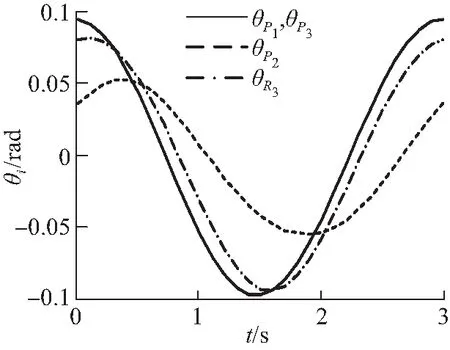
(a)理论角位移(a)Theoretical angular displacement

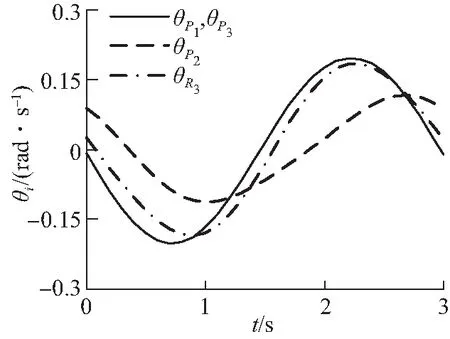
(b)理论角速度(b)Theoretical angular velocity

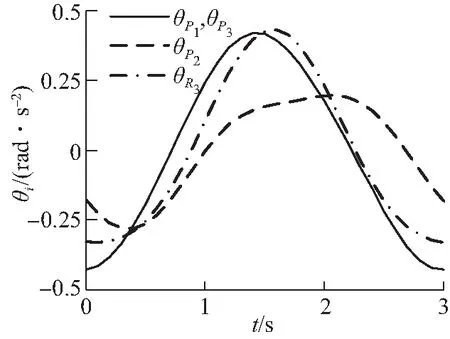
(c)理论角加速度(c)Theoretical angular acceleration

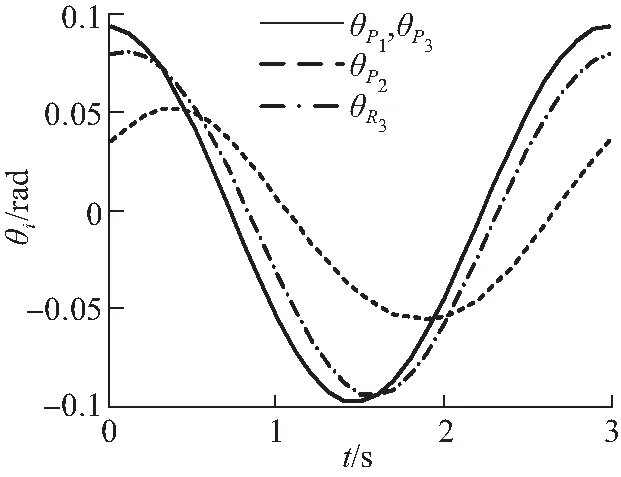
(d)仿真角位移(d)Simulation angular displacement

(e)仿真角速度(e)Simulation angular velocity

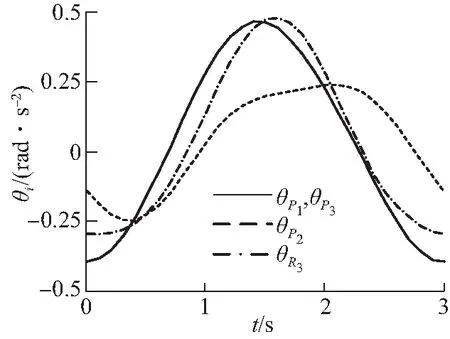
(f)仿真角加速度(f)Simulation angular acceleration图5 机构角位移、角速度及角加速度理论、仿真曲线Fig.5 Theoretical and simulation curves of angular displacement，angular velocity and angular acceleration of the mechanism

6 工作空间分析

并联机构的工作空间决定波浪能量转换装置浮子的运动能力。由于海洋波浪传播方向的不确定性，故取机构的灵活工作空间，即动平台中心GP点在z方向的不同位置处，β，γ所达到的转角集合。

对于波能转换装置机构，运动副的运动范围及杆件间的干涉限定了动平台的工作空间。

转动副的转角约束为：

(45)

其中：θR4为R1R2杆与R2R3杆之间的夹角，θR5为R4R3杆与R3GP杆之间的夹角。

球副与虎克铰的转角约束范围为：

(49)

虎克铰UP2与R3GP杆、R3R4杆间的干涉可以通过合理设计连杆的形状来避免，但转动副R3和虎克铰UP2的位置无法调整，故其运动副中心点的距离应满足约束条件：

DRU≥1 m.

(50)

结合式(45)～式(50)及波能转换装置位置反解利用极坐标搜索法绘制机构工作空间三维图，如图6所示。

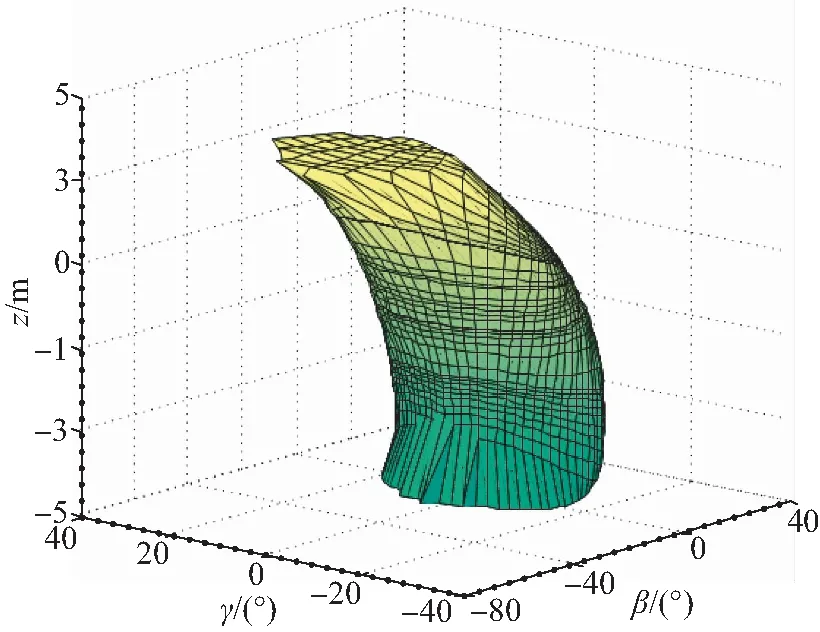
图6 机构工作空间三维图Fig.6 Three-dimensional graph of workspace

通过分析图6和图7可知，工作空间沿OPxz平面对称，与机构的对称性相吻合，当浮子沿z轴的运动范围为-3～0时，浮子能够绕任意水平轴转动±10°，减小z向的移动范围，能够增大转角转动能力，合理调整结构参数能够增大工作空间。

7 运动学性能评价指标

机构的运动学传递性能与波能转换装置的寿命和能量损失有直接关系。海浪发电装置通过浮子运动来采集波浪能量，然后通过波能转换装置将运动传递到运动转换装置，之后可以直接带动发动机运转，也可以转换为液压能再带动发电机运转。如果转换过程采用液压系统传递能量，在液压缸所受被动力和缸径一定的前提下，油液流速与支链末端角速度成正比，液压系统中油液流速过高会导致能量损失过大，且液压元件急速动作产生冲击会损坏液压系统，还容易使管道产生振动。另外，机构支链末端角速度的响应快慢直接影响运动转换装置和液压缸的使用寿命。

利用雅克比矩阵的最小奇异值来控制支链末端杆件的角速度[17]，最小奇异值越大，支链末端杆件对浮子运动的响应越慢，即浮子运动速度一定的前提下，最小奇异值越大，末端杆件的角速度越小，雅克比矩阵的最小奇异值可表示为：

(51)

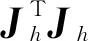
根据图6所示的工作空间，令zGP分别取值为[1，0，-1，-2，-3，-4]，利用式(51)绘制工作空间内运动学性能指标σ分布图，如图7所示。

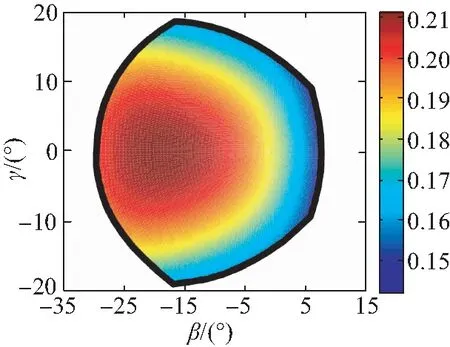
(a)zGP=1 m

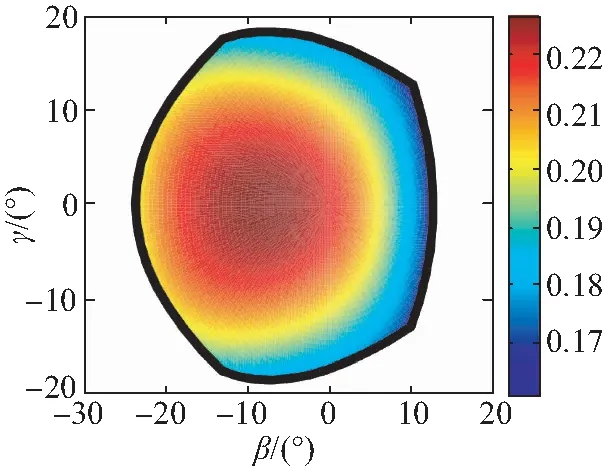
(b)zGP=0

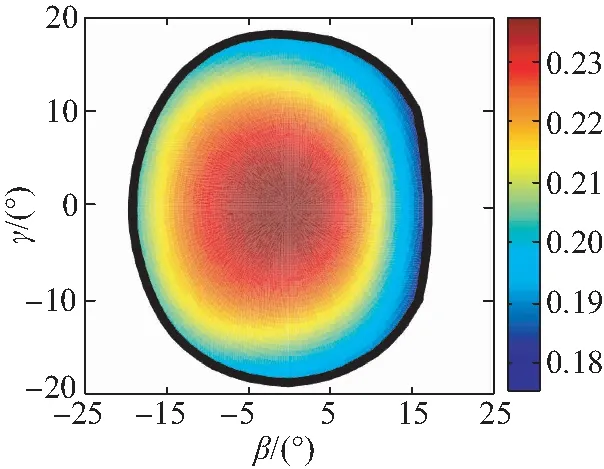
(c)zGP=-1 m

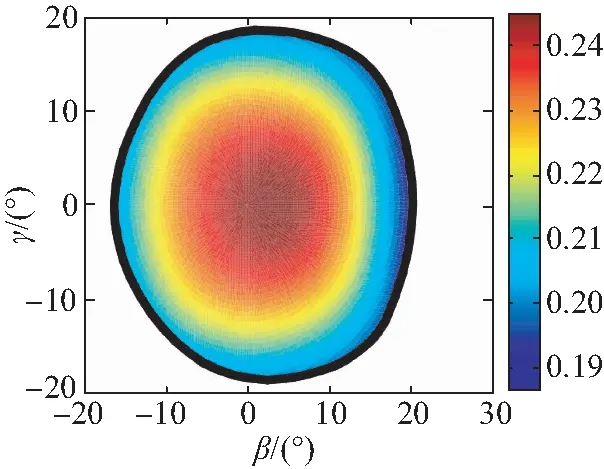
(d)zGP=-2 m

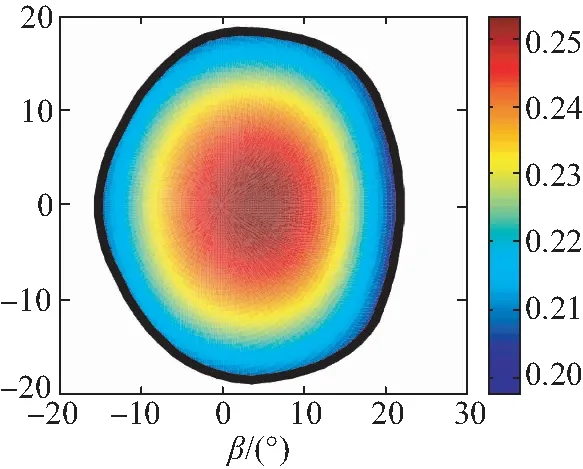
(e)zGP=-3 m

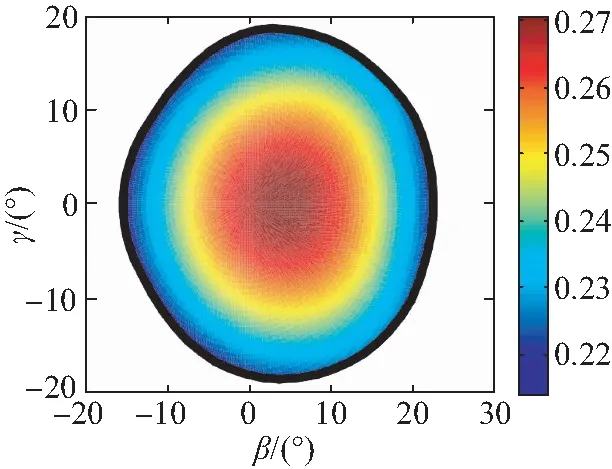
(f)zGP=-4 m图7 运动学性能指标在工作空间内分布图Fig.7 Distribution of kinematic performance index in the workspace

通过分析图7可知，运动性能评价指标σ的分布沿轴线γ=0对称，与机构结构的对称性相吻合，浮子在z向不同位置时，σ的变化范围均不大，介于0.15～0.3之间，且浮子转角在靠近工作空间中心位置时，运动学性能相对较优。

8 结 论

本文提出了一种能够实现一维移动和二维转动且含有冗余支链的三自由度并联机构，并基于该机构设计了海浪发电装置的能量采集转换机构。首先浮子垂荡与纵摇运动的耦合方程以及建立了浮子形状和尺寸与波浪能量采集效率的关系。然后建立了机构动平台与支链的速度、加速度映射关系，利用ADAMS软件仿真验证了理论模型的正确性。最后求解了机构的工作空间，基于雅克比矩阵的最小奇异值分析了机构的运动学性能。结果表明：圆柱体浮子适用于波浪周期变化较小的海域，球形浮子适用于波浪周期变化较大的海域；机构的工作空间满足海浪发电装置浮子的运动要求，且在工作空间内机构的运动学性能良好，靠近工作空间中心处性能最优。