面向低分辨率单目内窥镜图像的三维多孔结构重建

张建勋，韩明慧，代 煜*

(1.南开大学 人工智能学院，天津 300350； 2.南开大学 机器人与信息自动化研究所，天津 300350)

1 引 言

内窥镜是一种可以经由狭窄通道进入人体器官或者是工业设备内部进行观测的仪器。其产生和发展突破了人眼的视觉限制，为人体内医疗疾病的诊断和工业设备内部缺陷的检测提供了诸多便利。内窥镜的应用场景中经常出现多孔结构。类管道结构的多次分支是形成多孔结构的主要原因。在医疗领域，气管进入肺中层层分支形成支气管，输尿管进入肾脏产生分支形成不同的肾盂和肾盏；在工业领域，使用内窥镜频率较高的锅炉供水管道和设备通风排气管道等管道设备也常常呈现出多分支的结构。除此之外，工业检测对象上的类孔缺陷、块状锈斑等也与本文研究的多孔结构的概念相似。单目内窥镜虽然能获取影像，但是在探头尺寸的约束之下，其视野范围非常有限，只能观测到局部的二维图像，在呈现多孔结构的关键位置不利于分析和判断。鉴于此，实现基于单目内窥镜图像的三维重建，将有助于在复杂管道结构中获取孔洞的位置和尺寸等信息。

从运动中恢复结构算法(Structure from motion，SFM)已经广泛应用于相机运动跟踪和三维重建等研究中[1-4]，然而内窥镜的使用环境具有很强独特性，对于传统SFM算法的应用存在以下缺陷：(1)受内窥镜直径的限制，其输出图像的分辨率普遍较低；(2)人体器官内和工业设备内管道表面的纹理特征不明显；(3)管道内部、深孔等区域往往没有良好的照明条件，因此内窥镜大多自带光源进行照明，容易出现照明不足或者过强的情况；(4)管道内部常有气泡、浮尘等漂浮杂质[5]。国内外关于内窥镜图像的三维重建方面的研究已有一些成果。对于工业内窥镜，其三维成像的研究很少，郭俊锋等[6]和杨东林等[7]均通过设计双目光学系统获得图像的深度信息，这类方法的缺点是需要改变内窥镜的现有结构，并且增加了内窥镜探头的直径。相比之下，关于医用内窥镜三维重建的研究较多。Ben-Hamadou等[8]利用内窥镜实现了膀胱表面重建，但是为了降低特征提取的难度，需要额外投射激光点作为特征点。Sun等[9]利用SFM算法在从胃镜视频中进行表面重建，但是需要借助电磁跟踪装置来估计相机位姿。Visentini-Scarzanell等[10]在CT数据上训练卷积神经网，实现了对支气管镜图像的深度估计，但是这类方法只能恢复单幅图像的深度，不适用于重建完整的三维多孔结构。Mahmoud等[11]在使用ORB-SLAM进行稀疏重建的基础上提出了一种对猪肝脏表面进行稠密重建的方法，但重建对象表面的纹理密度会影响ORB特征点的密度，进而影响相机位姿估计的准确度。Turan等[12]改进阴影恢复形状算法用于胃肠表面重建，此方法假设表面没有阴影区域且较为平滑，然而孔洞的存在会使表面梯度发生强烈的变化，灰度也会明显降低，难以满足算法的假设条件。以上现有工作的共同缺点是无法同时满足以下两个条件：不借助外部设备和工具且不改变内窥镜的硬件构造；适用于弱纹理的多孔结构。

考虑到以上问题，本文提出了一种适用于低分辨率单目内窥镜对多孔结构进行三维重建的完整方案，创新之处在于：

(1)引入重建前期的图像预处理过程，基于加权引导滤波设计了多尺度图像增强方法用于提升图像的纹理细节，在不改变内窥镜结构且不额外增加辅助工具的情况下提高弱纹理环境下特征点的密度。利用快速行进算法(Fast Marching Method，FMM)修复漂浮杂质和高强度照射引起的高亮区；

(2)在SFM过程中，提出了一种简易快速剔除离群点对的方法，从而提高了低分辨率图像特征点匹配结果的准确性；

(3)由于尚未发现有研究工作涉及单目视觉下多孔结构的重建，本文提出了一种基于模板匹配和最小二乘拟合的三维多孔结构提取方法。

2 多孔结构三维重建方法和流程

2.1 基于加权引导滤波的多尺度图像细节增强方法

引导滤波[13-15]是一种需要引导图的局部线性滤波模型。当其引导图设置为原输入图像时，就成为了一种具有保持边缘能力的滤波器。在此基础上，Li等[16]提出了加权引导滤波算法，通过对图像上边缘强度的检测，自适应地调整引导滤波中的参数设置，消除了“伪边缘”现象，进一步提高了算法对图像边缘保持的能力。

本文基于加权引导滤波设计了内窥镜图像增强流程如图1所示。首先将原彩色图像按照RGB三通道分解成三幅单道图像Ix(Ir，Ig，Ib)。

图1 图像增强流程Fig.1 Flow chart of image enhancement

多尺度分解：对各通道的图像进行加权引导滤波，获得反映图片整体轮廓特征的结构图层：

Lx=F(Ix)，

(1)

其中F(·)代表加权引导滤波操作。然后使用原单通道图Ix减去其结构图层图像Lx得到各通道的纹理细节图层：

Rx=Ix-Lx.

(2)

接着对Lx进行相同的分解操作，得到不同尺度下的结构图层和细节图层：

(3)

其中：i代表分解的层级，Nm为其最大值。

图像重构：使用以下线性增强模型，实现对图像纹理细节的增强：

(4)

其中：Zx为增强后的输出图像，β为增强系数，用来拉伸各尺度下的细节图层，使纹理更加突出。

最后将RGB三通道增强后的图像叠加合并成纹理增强的彩色图像。此方法通过对图像的多尺度分解与重构过程，实现了在增强图像细节的同时保持边缘特性不变。

2.2 基于FMM的图像复原

本文利用FMM算法[17]去除由于漂浮杂质反光和内窥镜自带光源直射导致图像中产生的高亮区块，减少对特征提取和匹配的干扰。设计的图像修复流程如图2所示。经2.1节纹理增强后的图像作为待修复图像，经过二值化和形态学膨胀操作生成的图像作为修复模板，输入FMM算法模型中。此修复方法可以在不影响图像原始纹理结构的情况下实现对内窥镜图像中高亮区块的去除。

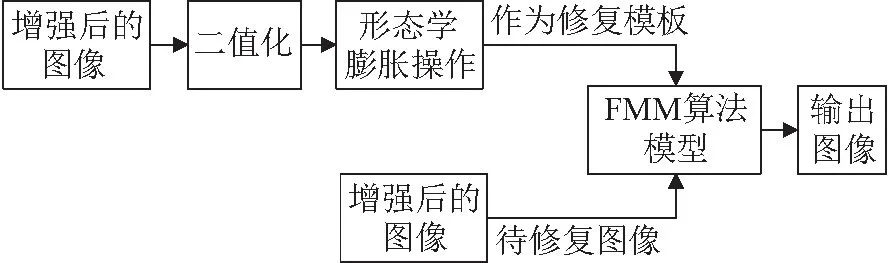
图2 图像修复流程Fig.2 Flow chart of image inpainting

2.3 引入离群点对检测的特征匹配与稀疏重建

本文采用基于SIFT特征的SFM算法进行稀疏重建，其一般包括特征匹配、相机位姿估计以及三维稀疏点云生成三个步骤。在特征匹配阶段，一般使用Ratio Test算法提高匹配的正确率。然而内窥镜图像相比于一般的相机图像清晰度低，即使经过Ratio Test仍然极易产生错误的匹配点对。因此本文提出了一种进行离群点对检测的方法，用在Ratio Test之后，进一步删除可信度低的匹配点对，优化匹配结果。

由于相机运动的平滑性，在同一次特征匹配结果中，每对匹配点在像素坐标系的X方向上的像素距离值原则上不会出现过大的差异，Y方向上亦如此。本文方法基于此假设，检测像素坐标关系表现比较异常的点对。图3所示为X坐标约束下的离群点检测算法，流程中，假设两幅图像通过初始匹配得到N对匹配特征点，算法统计了每个匹配点对中两点在像素坐标系的X方向上的差值，然后设计了搜索策略来搜索和定位离群点。多次实验表明阈值α在2～4之间取值时效果最佳。

图3 离群点检测流程Fig.3 Flow chart of outlier detection

将此流程图中的X都改为Y即可同理得到Y坐标约束下的离群点检测流程。在X坐标约束和Y坐标约束下标记出的离群点都视为错误匹配结果，进行剔除。通过离群点对的检测与删除，能够有效地去除特征相似但是位置关系异常的匹配点对，为下一步的相机位姿估计提供准确度更高的数据源。

2.4 三维多孔结构提取方法

现有的关于孔结构提取的研究均是基于双目视觉，如解则晓[18]等通过寻找极线与圆孔边缘的交点进行立体匹配重建圆孔轮廓。然而关于从单目SFM重建中提取多孔结构的研究尚未发现有报道，因此本文提出了一种基于模板匹配和最小二乘拟合的多孔结构提取方法。设计具体流程如下：

2.4.1 重建孔洞边缘三维点云

如图4所示，使用由SFM流程恢复的相机位姿信息，建立每对相邻关键帧之间的极线约束。pi为孔洞边缘上一点，将pi与其对应的极线上的每一个点进行模板匹配，使用零均值归一化互相关(Zero Mean Normalized Cross Correlation，ZNCC)匹配算法[19]计算相关度，相关度值最大的点视为与pi的匹配点。为了加快搜索过程，定义最小搜索深度dmin和最大搜索深度dmax：

(5)

其中dmean和σ分别代表当前帧对应稀疏点云的深度值的均值和方差。

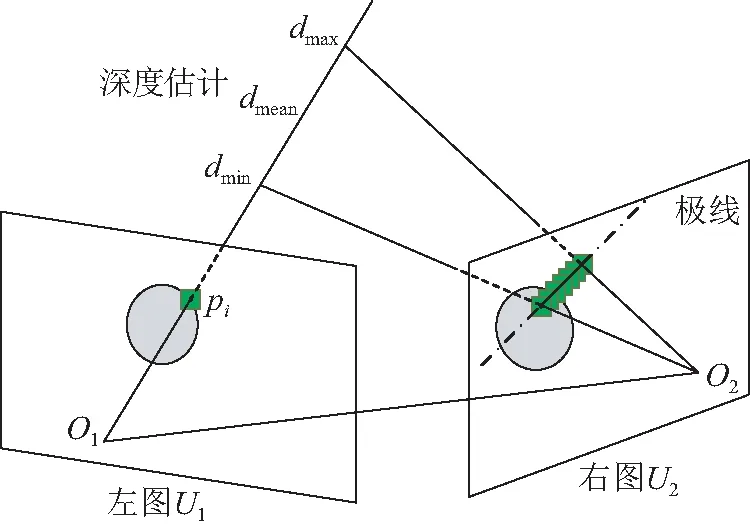
图4 模板匹配过程Fig.4 Process of template matching

在已知所有圆孔边缘点pi与其匹配点的条件下，结合已恢复的相机位姿信息，使用三角测量法即可得到孔洞边缘的三维点云Vcloud={P1，P2，P3，…}。

2.4.2 点云分割

由于点云Vcloud中包含多个圆孔，本文设计图5所示算法流程对点云进行分割。在实际应用时，可将P1与Vcloud中其余点的最短距离的3倍作为阈值e的取值。

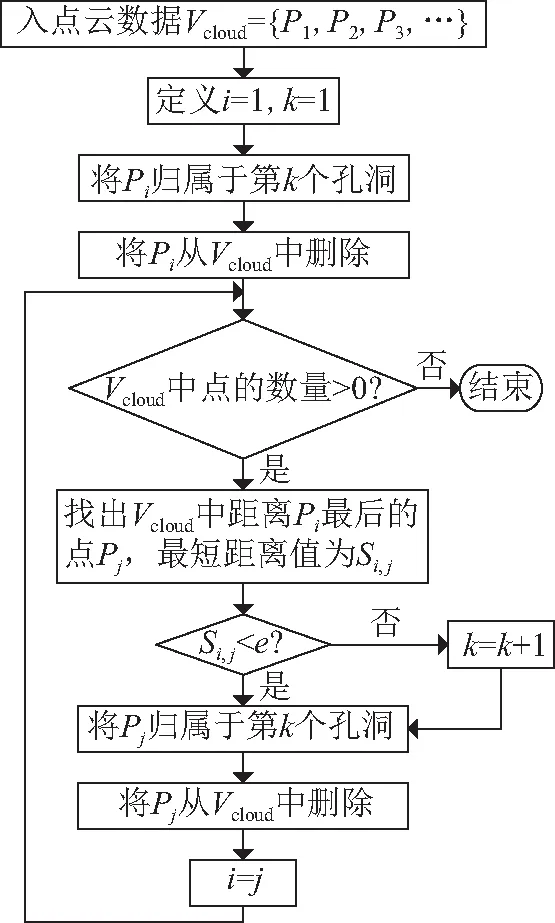
图5 点云分割Fig.5 Point cloud segmentation

2.4.3 计算圆孔的位置、大小和方向

本小节试图用三维空间圆去拟合每一个孔洞的三维边缘点集，从而获得孔洞的尺寸和空间位置关系。其中涉及到多次空间坐标系的变换，下面给出了各辅助坐标系的定义和变换公式的推导。

步骤1 如图6所示，利用最小二乘法对一个孔洞的三维点云进行平面拟合，得到拟合平面方程：

ax+by-z+c=0，

(6)

法向量[a，b，-1]的方向则代表当前圆孔的方向。将所有点[x，y，z]投影到拟合平面上得到[xp，yp，zp]，变换关系如下：

(7)

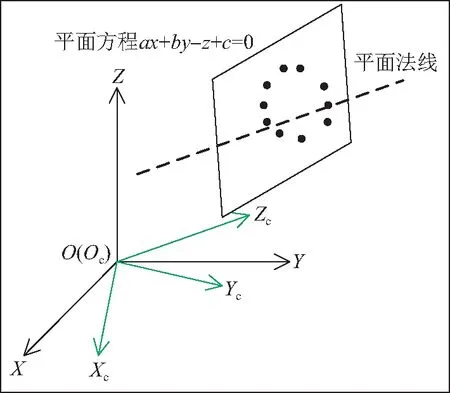
图6 坐标变换Fig.6 Coordinate transformation

步骤2 对圆的拟合一般要在二维平面上进行，因此需要将三维点坐标降维转换到二维平面上。创建一个新的坐标系Oc-XcYcZc，该坐标系的Zc轴与拟合平面的法线平行，Oc与O重合。假设坐标系O-XYZ绕X轴旋转θx角度，绕Y轴旋转θy角度可变换到坐标系Oc-XcYcZc。那么旋转矩阵表示为：

(8)

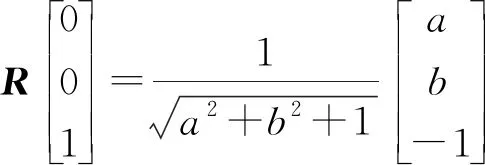
θy=arctan(-a)，

(9)

通过Pc=R-1P将投影到拟合平面的上的三维点转换到Oc-XcYcZc坐标系下，转换后所有点的Zc坐标值相同，因此可以在XcOcYc平面上进行基于最小二乘的圆拟合。拟合圆的半径即为当前圆孔的半径，拟合圆的圆心坐标经过P=RPc变换回初始O-XYZ坐标系下，作为当前圆孔的位置。

对重建图像序列中包含的每个圆孔，重复上述流程，提取出所有圆孔的三维结构。

2.5 重建方案小结

本文所提出的方案的完整流程如图7所示，现有的基于SFM的三维重建算法一般包括特征提取和匹配、相机位姿估计、稀疏三维点云生成三部分。但其在不借助辅助工具的前提下不能适应内窥镜图像和应用场景的特点，本文改进了现有的基于SFM的重建流程，使其能够在低分辨率的内窥镜图像上正常工作，并且最终提取出三维多孔结构。改进点如下：(1)使用基于加权引导滤波的多尺度图像增强算法，突显内窥镜图像的纹理细节，降低特征提取难度；(2)引入基于FMM图像复原算法，减小杂质对特征匹配的干扰；(3)在初始特征匹配后提出了离群点对检测算法，通过像素坐标位置关系的差异排除错误匹配结果；(4)提出了一种三维多孔结构提取算法。

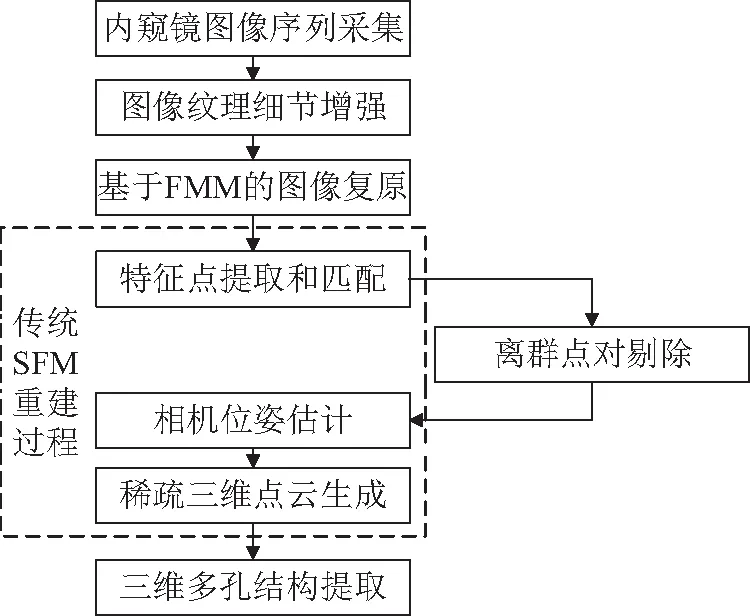
图7 本文重建流程总结Fig.7 Summary of reconstruction process

3 实验结果与分析

本文通过两组实验对提出的重建方法进行验证。第一组实验使用工业内窥镜对3D打印的多孔半球面进行重建，因模型参数已知，方便验证重建结果的准确性。第二组实验使用医用内窥镜对真实肾内多孔结构进行重建，验证本文方法的可行性。两种内窥镜均为单目内窥镜。实验的软件环境为Visual Studio 2015，64位Windows操作系统，C++语言编程，硬件采用Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz，8.00 GB内存。

3.1 利用工业内窥镜的多孔半球面重建实验

本文设计了直径为150 mm的多孔半球面，球面上的圆孔位置随机分布，直径取值为5～13 mm不等，如图8(a)所示。在半球面上粘贴了密度较为稀疏的纹理图。然后使用Anyty型号为3R-MFXS55的内窥镜对图8(a)中标号的8个圆孔进行拍摄，得到分辨率为720×480 pixel的图像序列。重建流程和结果见图8(b)～图8(h)。

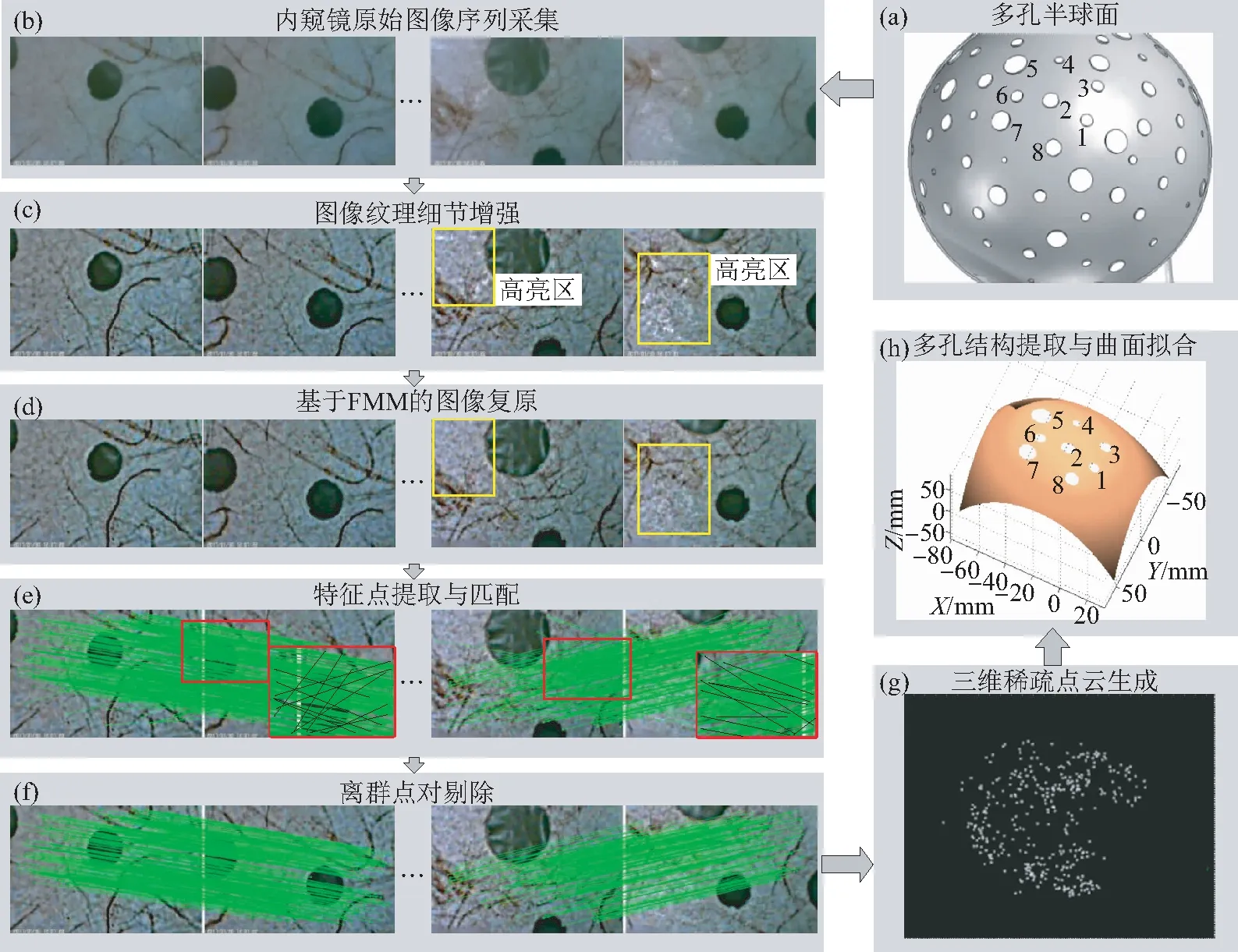
图8 多孔半球面重建过程和结果Fig.8 Process and result of reconstruction on porous hemisphere

3.1.1 图像增强与复原结果分析

实验时参数设置为：Nm=3，β=2，α=3。对比图8(b)和8(c)可以看出，使用本文方法进行增强后的图像纹理特征表现得更加明显，很多细小的纹理细节被突显出来，并且孔洞边缘的灰度梯度得到了良好的保持，这有利于最后多孔结构提取时对孔洞边界的准确定位。对比图8(c)和8(d)中的黄色框标记区域可见，使用本文的图像复原算法使得高亮区块得到了有效去除(彩图见期刊电子版)。

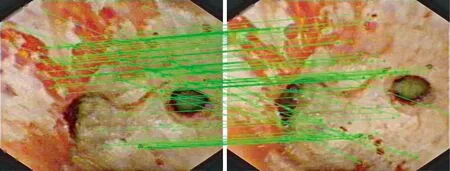
图9展示了未经处理的原始图像上的特征匹配结果，与图8(e)中的图像对比，能明显看出经过本文图像增强和复原算法处理后的图像上提取到的特征点数量相比于原始图像有极大提高。

图9 原始半球面图像上的特征匹配结果Fig.9 Feature matching on original images of the hemisphere

3.1.2 离群点剔除算法结果分析

在图8(e)中，对选取的相邻关键帧图像进行SIFT特征点提取和匹配。初始的特征匹配连线图中，正确匹配连线呈现出近似平行的状态，且长度接近。图8(e)右下角为红色边框部分的放大图，其中黑色线标记了部分异常连线，它们对应的是明显的错误匹配。由图8(f)可见使用本文所提出的离群点对检测方法，能有效地排除这些错误匹配点对。为说明本文离群点对剔除方法的优势，将本文算法与LOF算法[20]以及ORB-SLAM[21]中使用的旋转角度直方图统计算法进行对比，如图10所示，其中黄色圆圈标记出了结果中仍然存在的明显的错误匹配点(彩图见期刊电子版)。对比图10和图8(f)中的误匹配剔除效果，并综合考虑表1中各算法运行的耗时，证明本文算法的性能最佳。

(b)旋转角度直方图算法结果

表1 半球面重建中离群点对剔除算法的时间效率对比

3.1.3 多孔结构重建结果分析

为了验证本文方法的可靠性，重复进行了10组完全独立的重建实验，以下表格中展示的实验结果均为10次实验的统计数据。

对于位置分布关系的准确性，分别统计了真实模型(图8(a))和重建结果(图8(h))中1号圆孔圆心与其他圆孔圆心的距离值，以此距离值的误差大小作为衡量重建结果位置关系准确性的一个指标。由于单目重建出的三维结构与真实三维结构在尺寸上相差一个尺度因子，因此本文首先使用最小二乘法恢复尺度因子，基于此尺度因子，计算出重建结果在圆孔间距值上的相对误差。由表2可见，8个圆孔重建的相对误差都保持在10%之内。

对于圆孔大小的准确性，分别统计了多孔半球面和重建结果中各个圆孔的直径，进行对比。由表3可见，8个圆孔直径的重建相对误差也均在10%之内，满足实际应用的需求。

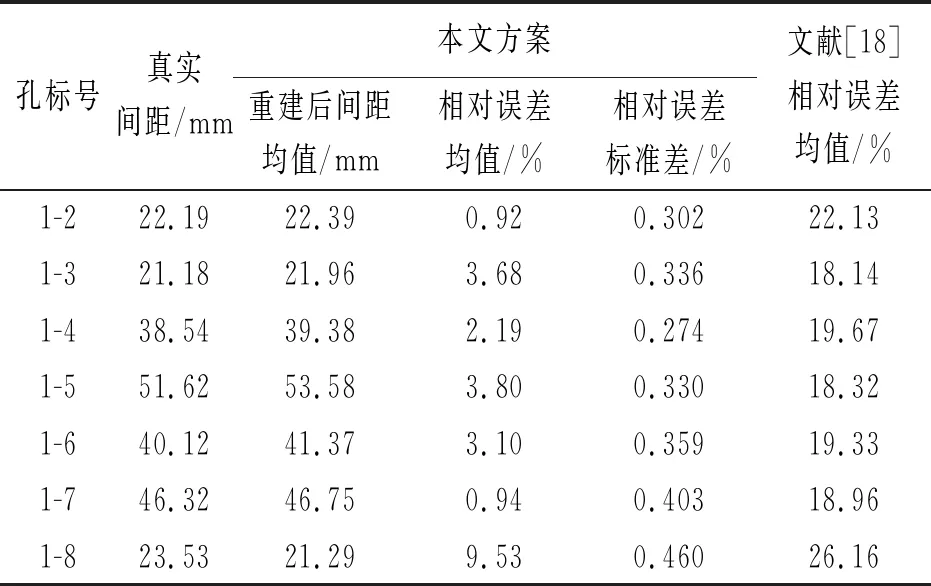
表2 圆孔间距误差

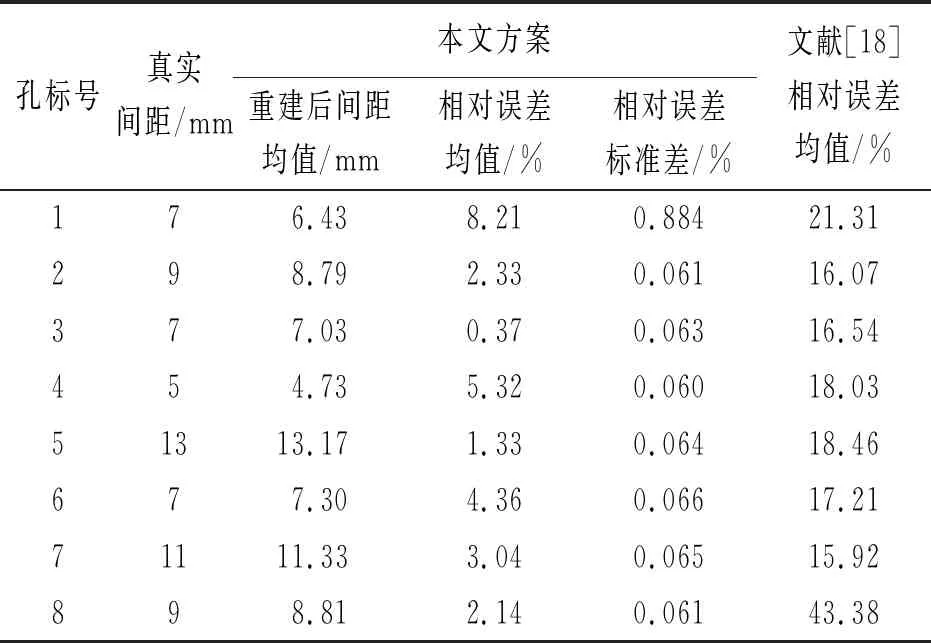
表3 圆孔直径误差

将文献[18]所述圆孔边缘点重建方法替换本文在2.4节提出的方案，得到对比实验结果，见表2和表3的最后一列。结合表4可见，相比于文献[18]，本文所提出的基于模板匹配与最小二乘拟合的多孔结构提取算法在轻微增加时间消耗的情况下，取得了较为明显的准确性的提升，总体性能更佳。对比实验的结果证明了本文方案更加适用于单目内窥镜。

表4 圆孔结构提取算法的时间效率对比

3.2 利用医用内窥镜的肾内多孔结构重建实验

本实验所用图像来自于北京民航总医院完成的经尿道输尿管软镜钬激光碎石取石手术，术中软镜经患者尿道和输尿管置入，到达肾脏并观察如图11(a)所示的肾内管道结构，所用软镜为奥林巴斯URF-V2型输尿管电子镜，图像分辨率为640×480 pixel。本文从内窥镜视频中截取了包含3个孔洞的片段，运用提出的算法流程重建此多孔结构，验证方法的可行性。

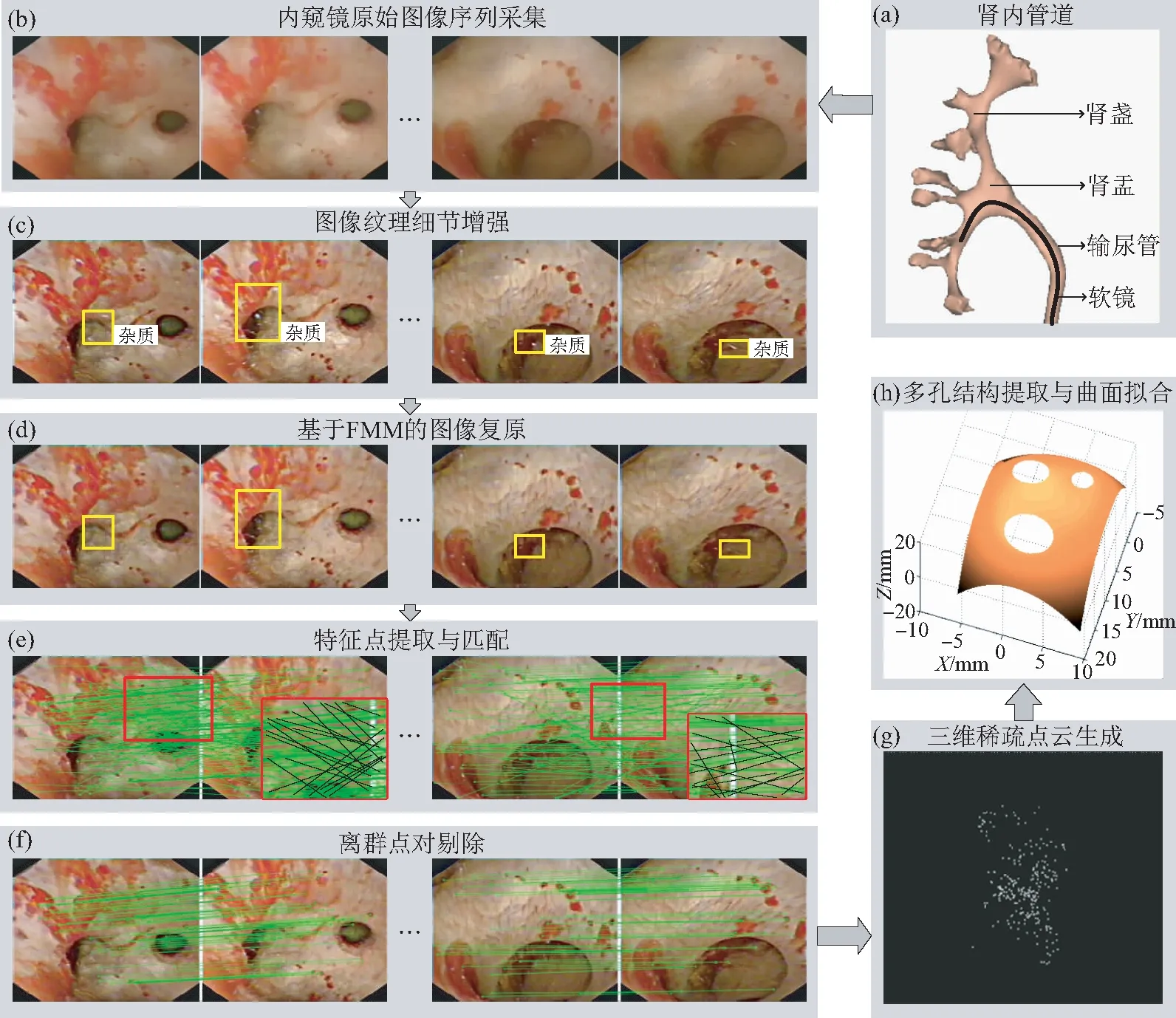
图11 肾内三维多孔结构重建过程和结果Fig.11 Process and result of porous structure reconstruction in the kidney

图11(b)～11(h)展示了根据本文提出的方案对真实软镜图像序列进行三维多孔结构重建的过程和结果。肾盂和肾盏中的血管，以及结石在移动过程中引起的出血，是重建中纹理的主要来源。

实验时参数设置与半球试验相同：Nm=3，β=2，α=3。图12展示了未经处理的原始图像上进行特征提取和匹配的结果，与图11(e)中图像对比，证明了本文所用图像增强和复原算法能够有效地提高特征点的数量。

表5 肾内重建中离群点对剔除算法的时间效率对比

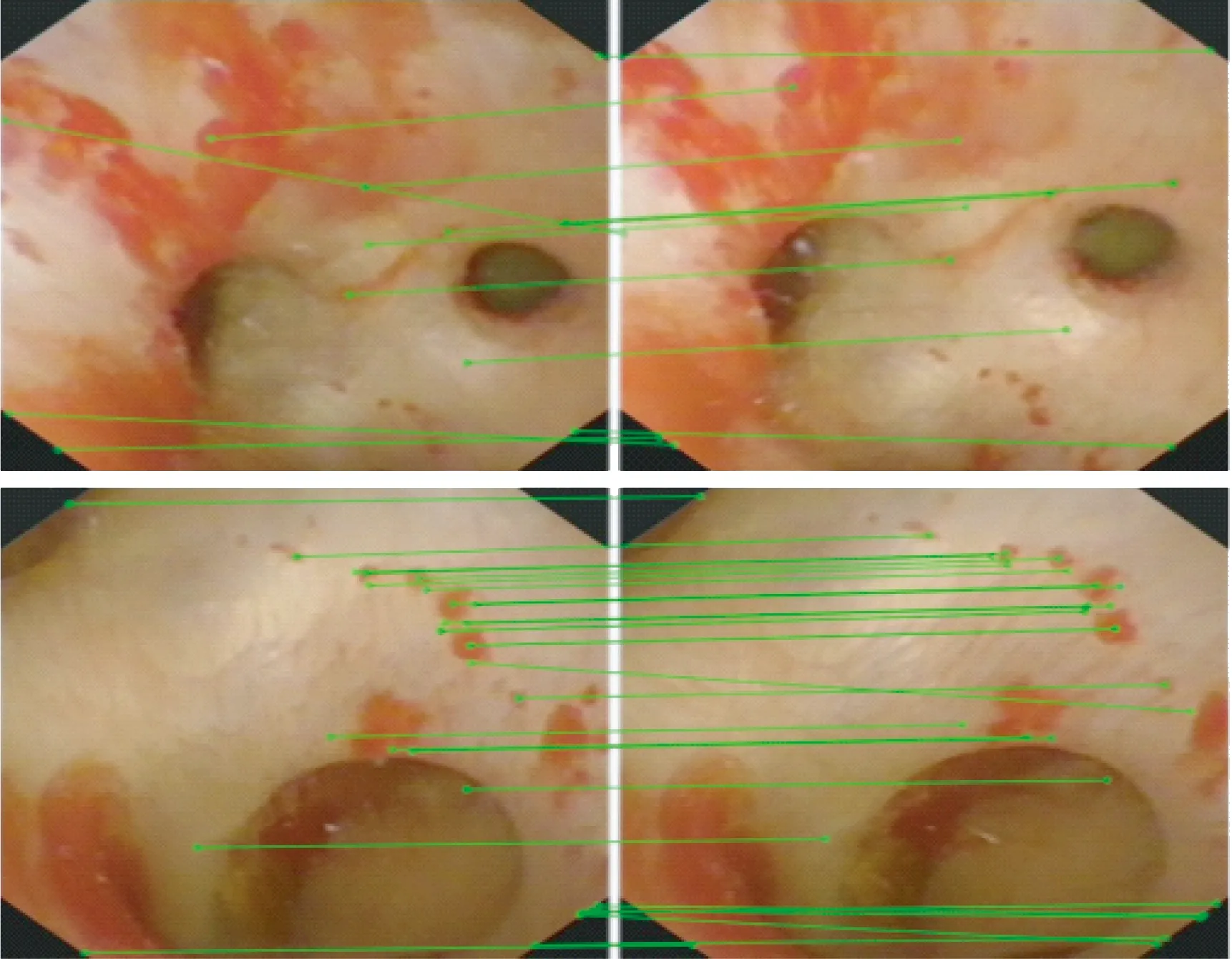
图12 原始肾内图像上的特征匹配结果Fig.12 Feature matching on original intrarenal images

通过图13与图11(f)中结果对比，结合表5中展示的各算法的耗时，证明了本文提出的离群点检测算法在真实肾内图像数据上依然表现出优势。由图11所示重建结果可以看到，使用本文重建方案最终得到的三个孔的大小和位置关系都与内窥镜视频所展示的内容非常接近，验证了本文整体重建方法的可行性。

(a)LOF算法结果

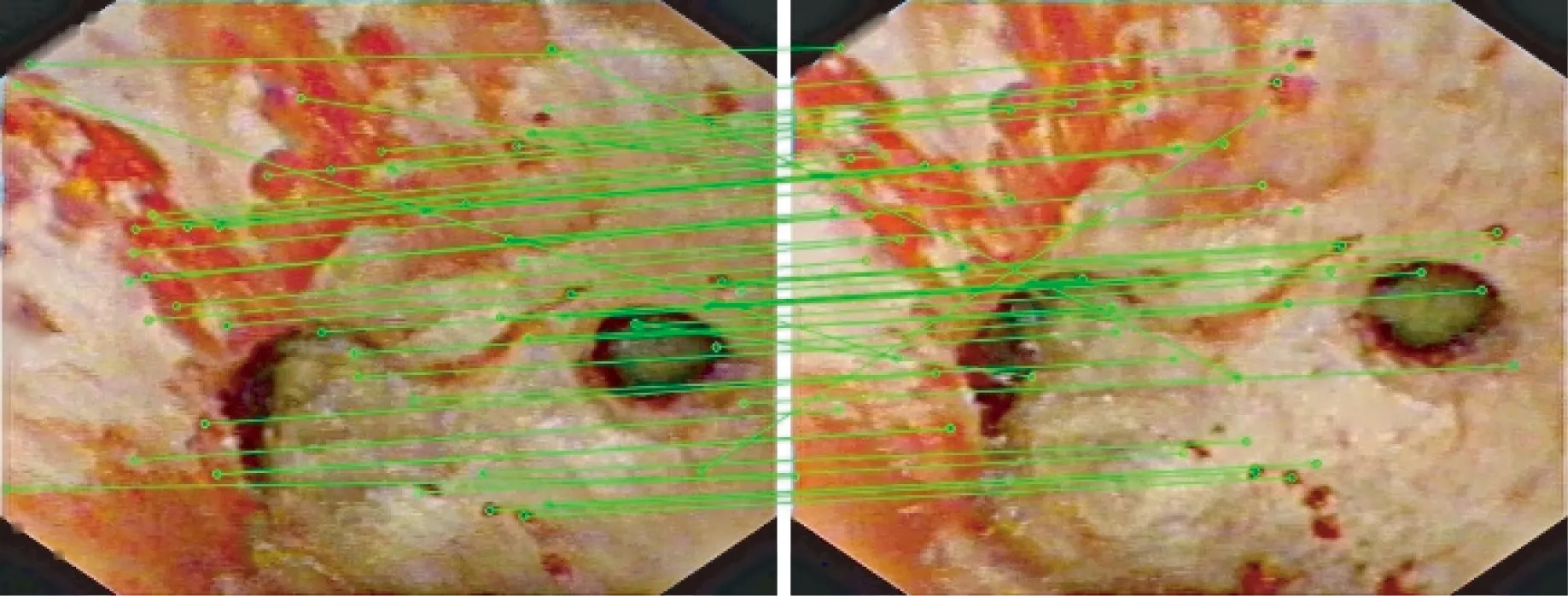
(b)旋转角度直方图算法结果

4 结 论

由于现有基于单目视觉的三维重建方法在不借助外部辅助工具的前提下难以在内窥镜的应用场景中运行，本文提出了一种面向低分辨率单目内窥镜图像的三维多孔结构重建方法。此方法具有以下特点：利用基于加权引导滤波的多尺度图像增强方法，增强了图像细节，克服了内窥镜本身成像清晰度低，且其应用场景纹理特征弱的缺陷，有利于特征提取；引入基于FMM的图像修复算法用于修补图像中的高亮区块，减少了气泡、漂浮杂质、表面反光等因素对特征点提取的干扰；提出了一种离群点对检测算法用于剔除错误匹配，优化特征点匹配结果，进一步削弱了内窥镜图像模糊对重建精度带来的影响；最后，提出了基于模板匹配和最小二乘拟合的多孔结构提取算法。多孔球面上的实验验证了整体算法流程的合理性和重建结构的准确性，重建结果中孔间距和孔直径的相对误差均小于10%。真实肾结石手术场景上的实验验证了本文方法的可行性。