改进SIFT快速图像拼接和重影优化

刘 杰，游品鸿，占建斌，刘金凤

(1.哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨 150080；2.工程电介质及应用技术教育部重点实验室(哈尔滨理工大学)，黑龙江 哈尔滨 150080)

1 引 言

近年来，图像拼接技术是计算机视觉以及虚拟现实(Virtual Reality，VR)领域的一个研究的热点。该技术在军事、汽车电子领域、医学图像以及图像遥感等领域被广泛应用[1-2]。然而图像的采集受到光照、环境以及相机视角等参数的影响，图像拼接得到的结果会出现失真、鬼影及曝光差异等问题。

当前，图像拼接算法可以分为基于空间域和频域两大类[3-4]。空间域主要应用的是基于特征的图像拼接，其特点对图像旋转、尺度缩放的性能较为突出，已被国内外研究者广泛地研究[5]，常见特征提取算法包括：加速鲁棒特征算法(Speed-Up Robust Features，SURF)[6-7]、旋转不变性二进制描述算法(Oriented FAST and Rotated BRIEF，ORB)[8-9]、尺度不变特征算法(Scale Invariable Feature Transform，SIFT)[10-11]等。其中SURF算法不能较好地保留边缘信息以及细节，ORB算法的计算速度快，但其二进制独立鲁棒特征(Binary Robust Independent Elementary Feature，BRIEF)不具有尺度不变特征。Lowe[10]提出的SIFT算法在尺度、旋转以及光照等变换上具有较高的匹配率，但对稳定点提取的速率有很大缺陷。Chin等[12]提出了基于SIFT算法的逼近投影变换，该算法将图像密集划分成网格，对每个网格进行投影，并给出了该算法高效的计算过程，但匹配速率相对较慢。牛燕雄等[13]利用高速分段特征检测器对特征进行提取，通过高斯差分算子简化搜索过程，提高了算法的速度，但对拼接图像出现的鬼影问题没有过多地考虑。吴磊等[14]利用多尺度递归网络对图像进行超分辨率重建，其结果对图像纹理和视觉效果得到明显的增强，但算法的复杂度高，处理时间长。虽然这些图像拼接算法在图像拼接质量及拼接速度方面都在不断改进，但针对的问题都比较单一，没有同时考虑算法的速度与图像质量的问题。

针对上述问题以及SIFT在无相似点搜索时间过长的问题，本文提出一种改进SIFT快速图像拼接和重影优化算法，提前划分有效的区域，减少图像配准在无效区域的时间。然后通过特征点计算最优拟合变换对图像进行投影，能有效减少图像拼接的重影问题。

2 图像拼接总体框架

本文提出的图像拼接算法包括图像获取、预处理、图像之间的相似性分块、SIFT算法的配准、多重投影拼接以及图像融合。具体流程如图1所示。

图1 图像拼接流程图Fig.1 Image stitching flowchart

图像拼接的第一步是从外界获取图像，由于对图像获取的设备不同，所采集的图像因设备或环境的不同，在一定程度会对图像拼接产生影响，所以需对图像进行预处理，以便减少外界因素所带来的影响。第二步是对图像进行区域分块以及特征点的提取和检测，通过计算图像信息相似性(Mutual Information，MI)值来判断是否为重合区域，以此依据来进行SIFT配准，能够有效的减少配准的时间。第三部分是图像的融合，将已经提取的特征点进行图像的拼接，现在多数的图像拼接都是通过已得到的特征点通过最小二乘法得到变换矩阵进行图像拼接，这种方法由于特征点集中区域不同，使得拼接的时候会出现鬼影或重影，虽然能通过融合算法进行淡化，但对复杂的环境效果较差。本文通过重合区域的多次投影进行投影矫正，使结果能有效的减少拼接所带来的重影问题，能有效的提高图像融合的质量。

3 图像配准

图像配准是整个图像拼接的核心，也是图像拼接算法最为复杂以及耗时的部分。通过图像的配准能将图像之间的特征点进行检测以及提取，将获取到的特征点通过计算得到图像的变换参数，从而根据参数进行图像之间的拼接。

SIFT算法是利用不同的尺度空间的图像进行相邻图层的极值点的寻找，并对该极值点进行描述，生成特征点。其优点是对图像旋转、大小无关，对光线、噪声、微视角改变等都具有很好的鲁棒性。因而在物体识别、地图感知与导航、图像缝合、图像追踪等领域应用广泛。算法的主要步骤为：尺度空间的极值检测，特征点的定位，特征点的方向确定，以及特征点的描述。

3.1 尺度空间的极值检测

尺度空间的建立主要是为了寻找空间上的极值点。将目标图像通过高斯函数对图像进行滤波，得到一系列平滑的图像，即为尺度空间。

一幅二维的图像I(x，y)通过二维的高斯核函数进行卷积来建立图像的尺度空间L(x，y，σ)，其表达式为：

L(x，y，σ)=G(x，y，σ)⊗I(x，y)，

(1)

(2)

其中：式(2)为高斯核函数，σ为尺度空间因子，该因子决定图像的模糊程度，其值越小图像细节越清晰。

3.2 特征点的定位

由于LoG(高斯拉普拉斯方法)效率不高，因此通过高斯金字塔，将相邻两层相减得到高斯差分函数DoG，由DOG来近似LoG进行运算：

D(x，y，σ)=(G(x，y，kσ)-G(x，y，σ))*I(x，y)=
L(x，y，kσ)-L(x，y，σ)，

(3)

其中k是相邻两个尺度空间的比例因子。

通过尺度空间的建立，获得高斯差分金字塔。为了获取高斯差分函数的局部极值点，对每一个像素点和它相邻的所有点进行比较，看是否比它的图像域和尺度域的相邻点大或小，若满足则该点为极值点，否则切换到下一个点进行比较。

通过上述的极值点获取方式会出现低对比度的特征点，为了剔除这些点将高斯差分函数进行Taylor展开式为：

(4)

对该函数进行求导，并令其导值为零。即：

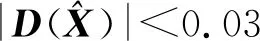
3.3 关键点方向确定

关键点是由DoG空间的局部极值点组成。利用特征点具有尺度不变性确定关键点方向，在高斯尺度图像的局部结构求得一个方向基准，之后利用图像的梯度直方图进行局部图像结构的稳定方向求取。像素梯度的幅值和幅角的计算公式如下：

(6)

(7)

3.4 关键点的描述符

以坐标轴旋转为最大值的主方向，将关键点作为中心，对附近邻域进行4×4的小区域提取，即16个子区域。将每个区域的360°幅角进行8等分，根据领域像素梯度幅度角的大小，将其归于

8个方向中，从而构成8个不同方向的向量，最终形成每个点128维的描述向量。描述向量通过欧式距离以及在选定范围的阈值进行比较，满足该阈值则可以作为该图像的匹配点。

4 图像相似性和二次投影描述

关键点的确定占整个SIFT算法时间的80%以上，同时传统SIFT图像拼接会带来重影的问题，为了提高无用区域的搜索时间以及减少重影的问题，本文提出了一种改进SIFT快速图像拼接和重影优化算法。

4.1 区域块

只有图像之间重合的区域才是有用的特征点，其他图像区域称之为无效区域。因此通过算法计算出图像重合区域能有效减少SIFT算法对图像搜索的时间。

对采集到的像素为x×y的图像，将其均匀分为n个区域块。每个区域块所消耗的时间为ti，用SIFT对两幅图像进行配准所需要的时间为2ts。一般场景中，用于图像拼接序列中，相邻图像的相似比例不低于40%[15-16]。如图2所示，左图为待匹配的图像，右图是参考图像。将图像分成5个区域块，根据划分块进行相关系数的计算，取系数大于0.82或重合区域较少时取系数最大值为特征点匹配区域。

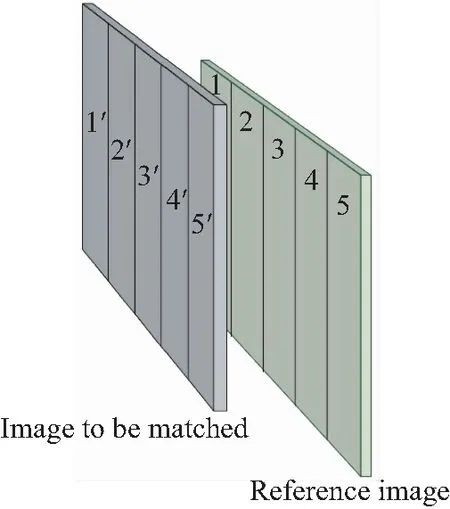
图2 区域分块Fig.2 Regional block

在图2中，将待匹配的图像中的1′区域与参考区域的1进行相关系数计算，依次往后是1′的区域与2区域进行计算，直到计算到5～5′部分结束，通过结果对比取相关系数最大的值为相似区域。本着两幅图像的相似区域太多在实际的生活中应用较少的原则，本次实验采集到的图像数据，其相似部分占整幅图像的3/5以内。在对两幅图像进行拼接时，传统的SIFT算法对两幅图像检测所需要的总时间为t=2ts，在相似区域块未确定之前，两幅图像所需要的总时间为t=2ts=5×5ti。当相似区域块确定时(假设检测到一个区域块)，单幅图像特征检测所需要的时间为ti，两幅图像特征点检测时间为t=2t≪2ts。因此，若能快速的判断图像相似区域，就能极大地缩减SIFT算法的计算时间。

4.2 区域相似性

要想计算出重合区域块，需要对相似性的度量有着明确的标准。基于两图像之间的共享信息数量的相似性对光线和咬合的变换不敏感，有着很好的鲁棒性和精确性。将图像进行5等分，其中I1与I2是两幅要匹配的图像，相应的两幅图像的信息相似性MI为：

MI(I1，I2)=E(I1)+E(I2)-E(I1，I2)，

(8)

其中：

E(I)=-ΣgpI(g)logpI(g)，

(9)

E(I1，I2)=-Σg，hpI1，I2(g，h)logpI1，I2(g，h))，

(10)

其中：g和h分别是图像I1(x，y)和I2(x，y)的灰度值，pI1，I2(g，h)是g和h的相似性分布函数。通过计算MI的值的大小来确定两幅图像之间的相似性，进而判断该区域是否为两幅图像的重合区域。而通过提高MI的计算速度能快速的搜索出相似区域，该算法的简化可参考文献[17-18]。

图像之间的相似性是图像的一种固有的性质。不同区域的相似性是不一样的，当两幅图像之间的相似性越高，MI的值就越大。通过此种方法能够有效的减低SIFT算法的匹配时间，同时也能提高特征点的匹配率。

4.3 二次投影

为了将图像全部呈现在同一个平面上，需建立一个几何的空间坐标变换使得一幅图像能够通过坐标变换映射到另外一幅图像上。常用的坐标变换有刚性变换、相似变换、仿射变换和投影变换，考虑到图像在拍摄过程处于的环境不同以及图像获取方式所带来的图像特征的不同，采用投影变换完成图像之间的投影坐标变换。其变换的模型为：

(11)

对一些简单的图像，第一次投影变换就能很好的将图像进行拼接，但对于相对复杂的环境时，投影变换的直接拼接会造成很严重的重影以及鬼影问题。所以有必要对拼接的图像进行鬼影的消除或减弱。由公式(11)得到投影矩阵H，通过矩阵H将图像进行第一次拼接。

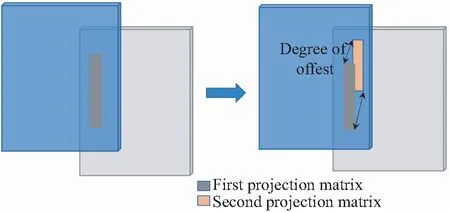
图3 矩阵偏离示意图Fig.3 Matrix deviation diagram

(12)

(13)

4.4 图像融合

针对图像拼接之后，会在重叠的区域有着很明显的拼接痕迹、断裂感，需对图像进行融合的操作。对两幅图像I1与I2的重合区域进行渐入渐出加权平均算法融合操作，其原理如公式(14)所示：

(14)

其中：I1与I2是两幅要匹配的图像，α为权重系数其取值范围为0～1之间，重合区域变换的规律是I1的重合区域图像从0到1变换，I2的重合区域是从1到0之间的变换规律，根据此原理拼接之后的重合区域能够实现平滑，达到拼接之后从视觉上看是一张图像的效果。

5 实验结果及分析

实验所用平台的CPU为Inter i5-8300H@2.30 GHz，内存为8 G的Windows7系统下完成，软件平台为：MATLAB9.3(R2017b)。

为了对本算法的鲁棒性进行验证，本文对图像的缩放、添噪声、平移等几个方面进行验证，具体的实验数据结果如图4所示。从图4中可以看出，在不同的干扰下，本算法能够有很好的鲁棒性。因此本算法能够稳定地进行图像的特征点匹配。

图4 鲁棒性测试图Fig.4 Robustness test diagram

通过将图5进行五等分区进行区域块的相似性判断，其中A与A′相对应，B与B′相对应，以此类推。结果如图5所示，对参考图像以及待匹配的图像进行分区。

图5 两幅分割图像Fig.5 Two segmented images

利用传统区域灰度平均值作为辅助测量方法[19]，结果如图6所示，左图和右图的横坐标都是区域的分块部分，其中数值对应的分块部分为A-A′，A-B′，A-C′，…，E-E′，左图的纵坐标是MI相似性数值，右图纵坐标是像素灰度值的均差。图像信息相似性MI值越大说明图像之间的相同区域关系就越大，与之相反的其均差就越小。从图6中可以看到，在左图中D-A′与E-B′两个区域的所对应的MI值相对较高，其值分别对应0.91与0.84，右图中的灰度值的均差部分在D-A′与E-B′区域的均值最小，其值分别对应0.002与0.003，MI值最大的两个区域与均值最小的两个区域是一致的，由此可以看出这两块所对应的区域是重合最多的部分。

图6 区域块测量Fig.6 Area block measurement

本文通过3组不同角度的图像数据进行相似性分块，与文献[11]，文献[13]，APAP[12]，ANAP[20]的特征提取算法进行比较，其中文献[11]采用SIFT+RANSAC算法进行图像拼接，文献[13]采用高速分段特征检测算法进行图像拼接。实验数据的像素大小分别为600×800 pixel，512×683 pixel和320×427 pixel，如图7所示。其中实验结果的数据如表1所示。

图7 手持相机拍摄图像Fig.7 Photographs taken by hand-held cameras

由表1可以看出，本文提出的分块算法在特征点检测上有着明显的速度提升，较文献[11]的算法提高大约58%，与文献[13]相比提高大约14%。而APAP与ANAP算法对特征提取无算法优化，所以结果与文献[11]相差不大。

如图8所示为算法拼接比较，在图8(a)中，图像拼接的效果从上至下不断提高，可以看到文献[11]，文献[22]，APAP，ANAP这四种算法重合部分还是出现局部的重影，而采用本文算法重合部分的重影基本去除；在图像(b)中，其他四种算法都在图像的局部出现重影或对齐之后线条消失的情况，而本文算法的拼接结果要优于其他算法，其结果无明显的图像的重影问题。从图8的拼接结果可以明显看出本文的二次投影拼接效果明显。

为了验证本文的图像拼接算法的效果，现给出三组在不同角度以及场景下进行拍摄的图像数据对算法进行验证，其拼接的结果如图7所示。通过较为常用的图像客观评价指标——结构相似性(Structural Similarity，SSIM)[21-22]以及边缘差分谱评价法(Difference of Edge Map，DoEM)[23]对拼接的图像进行质量评价。

SSIM算法的评分内容主要体现在：亮度、对比度、结构。具体公式如(15)所示：

(15)

其中：μX与μY分别表示图像X与Y的方差，σXY表示图像X与Y的协方差，C1与C2为常数，通常取C1=(K1×L)2，C2=(K2×L)2，一般地K1=0.01，K2=0.03，L=255。

DoEM算法主要注重图像拼接部位是否有错位以及边界过渡是否平滑等方面[23]，其算法评价的内容有三个步骤：图像边缘检测、图像边缘差分谱构建、统计差分谱信息并计算评分。其具体公式如(16)所示：

(16)

其中：μe为边缘差分谱过渡区域边界区均值，μa为过渡区域整体均值，σ2为过渡区域整体方差。C1，C2，C3，C4分别为4个常量，设定参数为：C1=80，C2=50，C3=600，C4=256。

其图像质量提升率用Quality表示，计算方式如(17)所示：

Quality=(M-N)×100%.

(17)

通过SSIM算法与DoEM算法对三种图像拼接的结果进行质量对比，与文献[11]相比本文算法在图像质量上提升约10%，与文献[22]相比提升约5%。与APAP相比提升较明显，而对于ANAP虽然提升约2%，但是本文的特征点提取速度有着显著提升。说明了本文算法的有效性。

表2 SSIM与DoEM拼接质量对比

6 结 论

本文针对SIFT算法在实际应用中的实时性问题以及图像拼接出现的重影所带来的质量问题，提出了改进SIFT快速图像拼接和重影优化算法，并通过算法的运行时间以及图像质量等参数指标验证本算法的可行性。在运行时间方面，通过图像之间的相似性搜索出两幅图像的重合部分，减少无用区域搜索时间，与SIFT相比，特征点检测时间提高了58%。在图像质量方面，通过最佳拟合相似变换找出最优投影矩阵对图像质量进行优化，采用两个客观评价指标对图像进行客观评价，其评价指标结果要优于其他算法。实验结果表明，本文提出的算法能够有效的降低SIFT算法的时间以及提高图像拼接的质量，验证了算法的有效性。