激光跟踪仪多测站抗差马氏光束法平差

郭迎钢，赵文斌，李宗春，张冠宇，杨 浩

(1. 战略支援部队信息工程大学，河南 郑州 450001；2. 中国科学院 上海高等研究院，上海 201800)

1 引 言

激光跟踪仪是将精密激光测距技术和精密角度测量技术相结合而研发出的一款精密测量仪器[1-2]，坐标测量精度可达几十微米，具有快速、动态、高精度等特点，在航空航天、机械加工制造、大型设备精密安装、计量检定等领域有着广泛应用[3-7]。为了提高基于激光跟踪仪空间坐标测量的精度、效率和适用范围，国内外学者从仪器现场检定与校准[8-9]、合作目标检测[10]、建网模式优化[11-12]、解算模型完善[13]、测量不确定度评定[14]、受限空间内精密坐标传递[15]等方面开展了广泛而深入的研究。

在大型复杂设备安装测量及空间目标姿态测量中，由于被测目标尺寸较大或者存在遮挡，难以在一个测站完成测量任务，需要多次设站或者多台仪器联合测量[16]，因此需要对多测站进行平差解算，同时求解被测点坐标及激光跟踪仪测站的位置和姿态参数。激光跟踪仪的多测站数据处理涉及函数模型、随机模型的建立，平差基准的选择，粗差的定位与剔除等问题，作为一个研究热点，许多学者围绕这些问题进行了研究[17-19]。关于激光跟踪仪多测站平差模型的研究，1998年，Meid[20]对激光跟踪仪光束法平差的权重、约束条件等进行了研究，提出了加权光束法平差模型。2002年，Calkins[21]在光束法平差的基础上研究了统一平差计量网络(Unified Spatial Metrology Network，USMN)，并应用于Spatial Analyzer(SA)软件。2010年，Predmore[22]在考虑每个测量点不确定度椭球的形状和方向的基础上，基于多元统计中的马氏距离建立目标函数进行多测站观测数据的平差解算，取得了很好的应用效果。2012年，周维虎等人[23]基于光束法平差模型研究了激光跟踪仪测量精度的评定方法。2018年，丁阳等人[24]研究了基于光束法平差的多测站激光跟踪仪数据处理，并指出观测值权值对平差结果影响较大。

受文献[22]的启发，本文对激光跟踪仪多测站抗差马氏光束法平差展开研究。在传统激光跟踪仪光束法平差的基础上，引入马氏距离的概念对平差准则进行改造，由原来的使“观测值改正数加权平方和最小”改造为使“观测值到加权平均值的马氏距离平方和最小”，并在计算加权平均坐标时对粗差观测值进行剔除，构建了激光跟踪仪多测站抗差马氏光束法平差模型。然后利用仿真试验和实测数据试验，对该模型的适用性及解算精度进行了测试。

2 算法原理

2.1 激光跟踪仪多测站测量

设激光跟踪仪的水平角观测值为H，垂直角观测值为E，斜距观测值为S，则第k号点在测站坐标系下的坐标为：

(1)

如图1所示，3台激光跟踪仪分别按自由设站法测量了空间内分布的一些控制点。由于不同测站观测的点坐标属于独立的测站坐标系，为了获取控制点在空间全局坐标系内的坐标，需要将多测站的测量数据转换到统一的测量坐标系下。

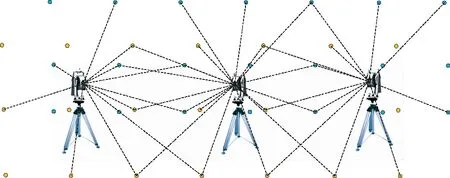
图1 激光跟踪仪多测站测量示意图Fig.1 Schematic diagram of laser tracker multi-station measurement

以三维七参数坐标转换模型为基础进行坐标转换。由于激光跟踪仪测距精度很高，各测站的尺度因子取为1，以第1测站为基准测站，第i测站坐标系先绕X轴旋转α、再绕Y轴旋转β、再绕Z轴旋转γ，再平移至第1测站坐标系的坐标转换模型为：

(2)

令R=R(γ)R(β)R(α)，则：

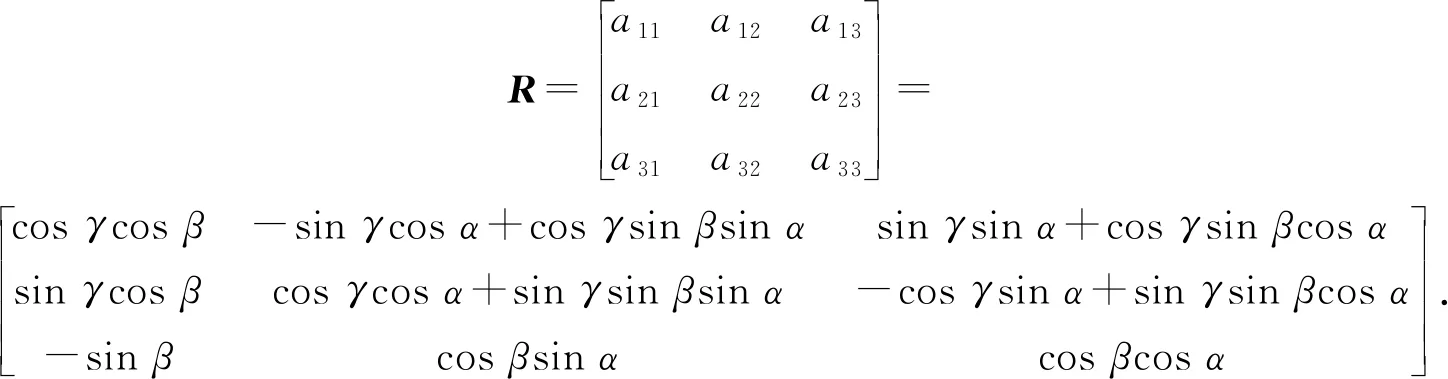
(3)

式(2)也可表示为：

(4)

2.2 光束法平差模型

假设激光跟踪仪在空间内布设了m个测站，对p个控制点进行了测量，则未知参数个数为：

t=6(m-1)+3p.

(5)

设总观测数为n，则多余观测数为：

r=n-t.

(6)

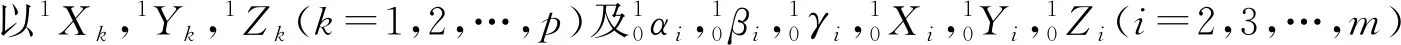
V=AδX+l，

(7)

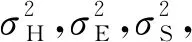
iΣk=BΣLBT，

(8)

其中：

根据观测向量的协方差阵定权，即：

(9)

式中σ0为单位权中误差。

以VTPV=min为平差准则，使所有目标点观测值相对于坐标最或然值的欧氏距离加权平方和最小，同时解算未知参数(包括控制点在测量坐标系内的三维坐标及测站坐标系向测量坐标系转换的旋转、平移参数)的最小二乘解，此即为激光跟踪仪多测站传统光束法平差(Traditional Bundle Adjustment，TBA)模型。

2.3 抗差马氏光束法平差模型

由式(8)可以得到第k号点在第i测站坐标系下坐标(ixk，iyk，izk)的协方差阵Σk。设第i测站坐标系到第1测站坐标系的旋转矩阵为(1Ri)T，则该测站观测的第k号点在第1测站坐标系下的坐标iXk=[1Xk，1Yk，1Zk]T对应的协方差阵为：

(10)

设m个测站均观测了第k号点，由于每个测站的观测值相互独立，根据误差传播定律，第k号点的协方差矩阵：

(11)

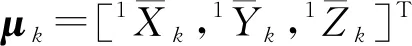
(12)

由马氏距离的定义可知，第i测站观测第k号点的观测值iXk到加权平均坐标μk的马氏距离：

(13)

m个测站均观测了第k号点，文献[22]中定义第k号点对应的平均马氏距离为：

(14)

然后以所有控制点的平均马氏距离平方和最小为平差准则，即：

(15)

文献[22]只考虑了观测值的先验精度，如果观测值中存在粗差，但其先验精度与其他观测值并无区别，按照式(10)～ 式(15)进行计算难以抵抗粗差观测值对解算结果的影响。而且，第k号点的协方差阵Σk是由其三维坐标的方差及协方差构成的。已知3×3行列式的几何意义为其行向量或列向量所张成的平行六面体的有向体积[25]，式(14)中将第k号点协方差矩阵行列式值的立方根|Σk|1/3作为权因子来求平均马氏距离，这种加权方法会使精度低、方差及协方差大的点在计算平均马氏距离时拥有更大的权重，是不合理的。

为此，本文在文献[22]的基础上进行改进。记第j测站观测值对应坐标jXk到加权平均坐标μk的残差为jvk，则：

(16)

然后判断ivk是否大于3倍单位权中误差。若是ivk大于3倍单位权中误差，则在计算第k号点的协方差矩阵及加权平均坐标时，第j测站对应的协方差和点坐标均不参与计算。即式(11)改为：

(17)

将式(12)改为：

(18)

定义第k号点对应的马氏距离：

(19)

然后以所有控制点的马氏距离平方和最小为平差准则，即：

(20)

据此，同时求解控制点在测量坐标系下的三维坐标及测站坐标系向测量坐标系转换的旋转、平移参数，称之为抗差马氏光束法平差(Robust Mahalanobis Bundle Adjustment，RMBA)模型。

3 试验与分析

为了验证RMBA模型的适用性及其解算精度，进行了仿真试验和实测数据试验。美国New River Kinematics 公司的SA软件是一款功能强大的工业测量软件，常用于处理激光跟踪仪多测站观测数据，经受了粒子加速器准直安装、航空航天部件装配、计量检定等领域的测量实践考验，其解算结果可以作为本文方法的比对对象。

3.1 仿真数据试验

设计了6 m×4 m×2 m空间内分布的12个控制点，拟用Leica AT402激光跟踪仪在4个测站位置分别观测这12个控制点。控制点及测站坐标见表1，空间分布如图2所示。

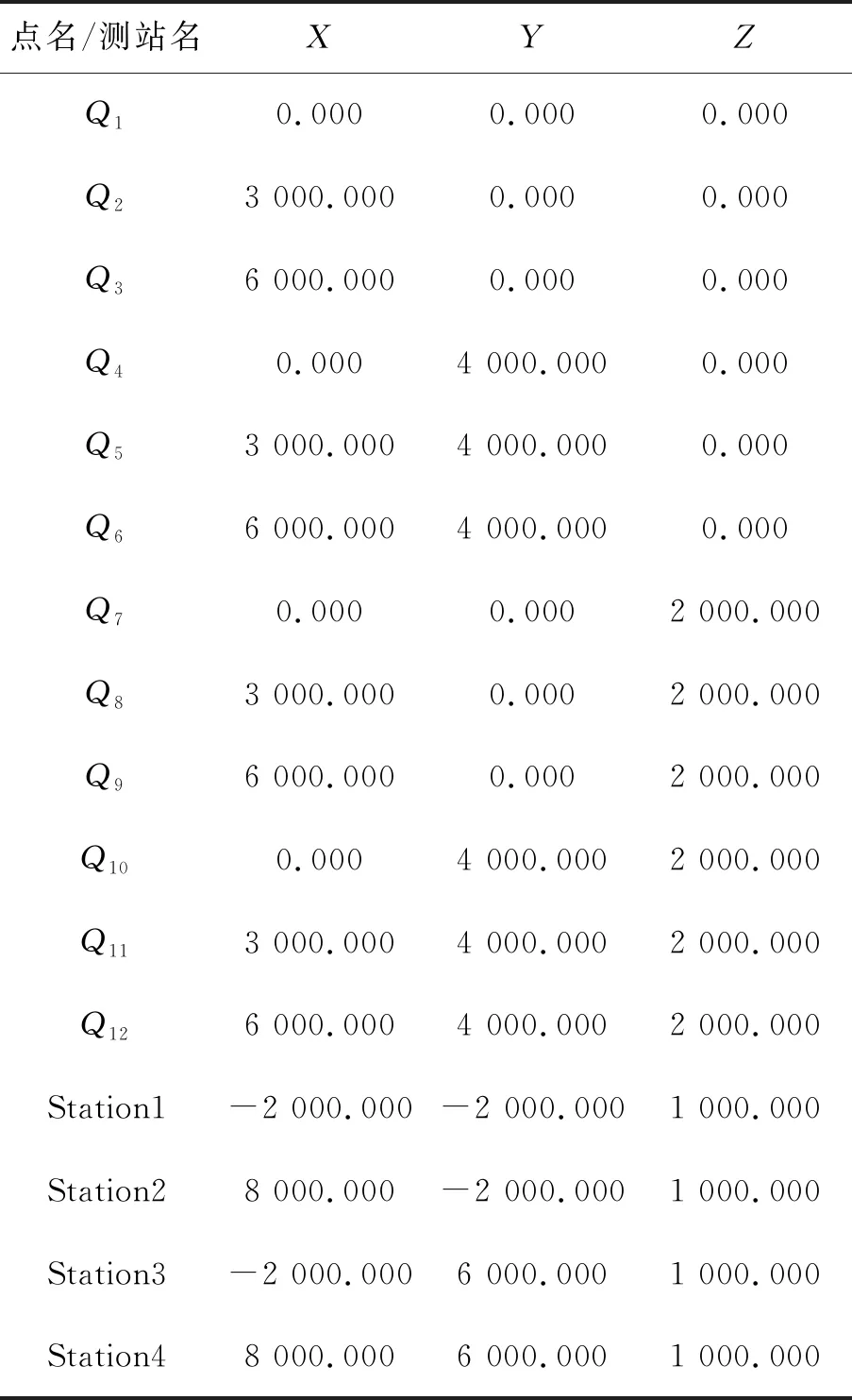
表1 控制点及测站坐标

图2 激光跟踪仪多测站模拟测量试验布局Fig.2 Simulation experiment layout of laser tracker multi-station measurement

以MATLAB为工具进行了模拟测量。根据12个控制点及4个测站的已知坐标，按照水平角1.5″、垂直角1.8″、斜距0.5 μm/m×D的测量精度，在相应的观测值上加入随机误差，模拟生成了每个测站的观测值。以第1测站坐标系为测量坐标系，分别按照TBA，RMBA，文献[22]方法和SA软件(2019.09.10版)4种方式处理仿真数据，解算的12个控制点在测量坐标系下的坐标与真值的三维偏差及其均方根(RMS)如表2所示。

表2 控制点三维坐标偏差及其均方根

由表2可以看出，对于该组模拟数据，TBA解算结果的坐标偏差均方根为0.057 mm，文献[22]方法解算结果的坐标偏差均方根为0.040 mm，SA软件解算结果的坐标偏差均方根与文献[22]方法的结果相近，为0.041 mm，本文提出的RMBA模型解算结果的坐标偏差均方根为0.031 mm。结果表明，TBA的解算精度最低，本文方法的解算精度优于文献[22]方法与SA软件的解算精度。

为了验证4种方法解算效果的稳定性，按照同样的方式随机又生成了10组模拟数据，对比4种方法对应的12个控制点坐标与真值的三维偏差均方根如表3所示。

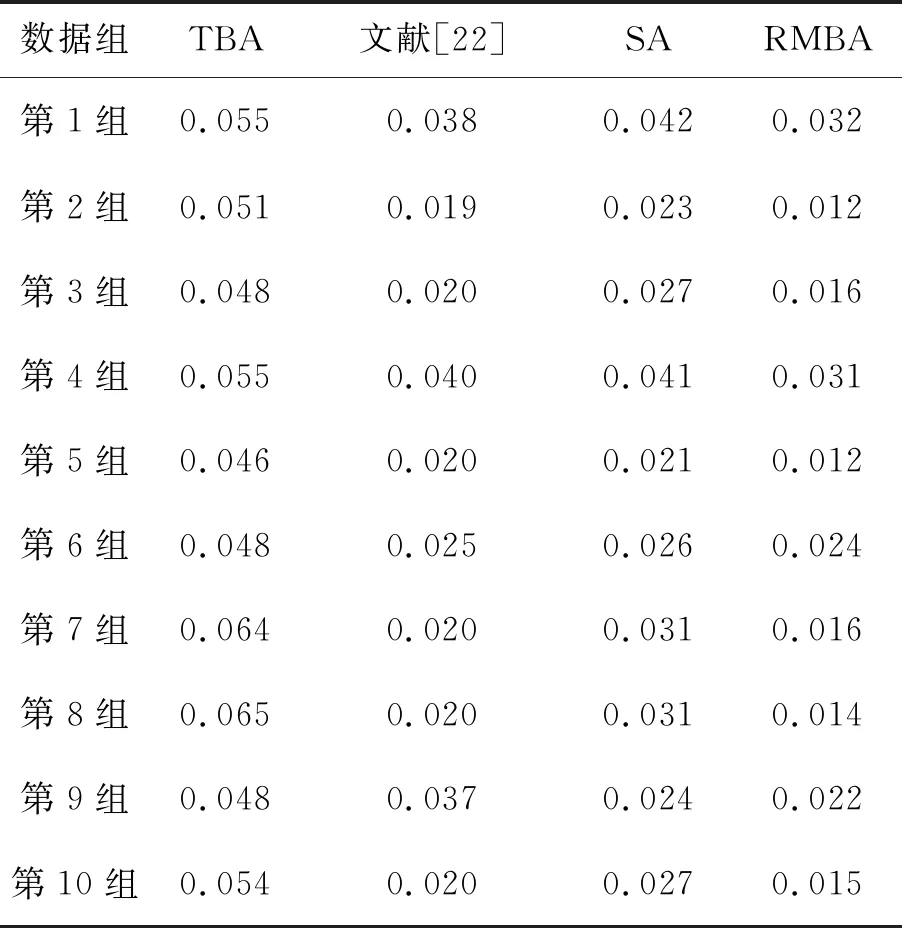
表3 控制点三维坐标偏差均方根

由表3可以看出，10组模拟数据的测试结果中，TBA的三维偏差均方根最大，文献[22]方法的三维偏差均方根在大部分情况下小于SA的结果，RMBA的三维偏差均方根均为最小，与表2中的结论一致，验证了4种方法解算效果的稳定性。

模拟测量试验的范围在10 m以内，测量精度约为±0.075 mm。为了测试不同方法的抗差性，在表2对应的模拟数据中测站1照准Q1的测距观测值加上0.20 mm，将其改造为粗差观测值。分别用4种方法处理此含有粗差的模拟观测数据，解算结果如表4所示。

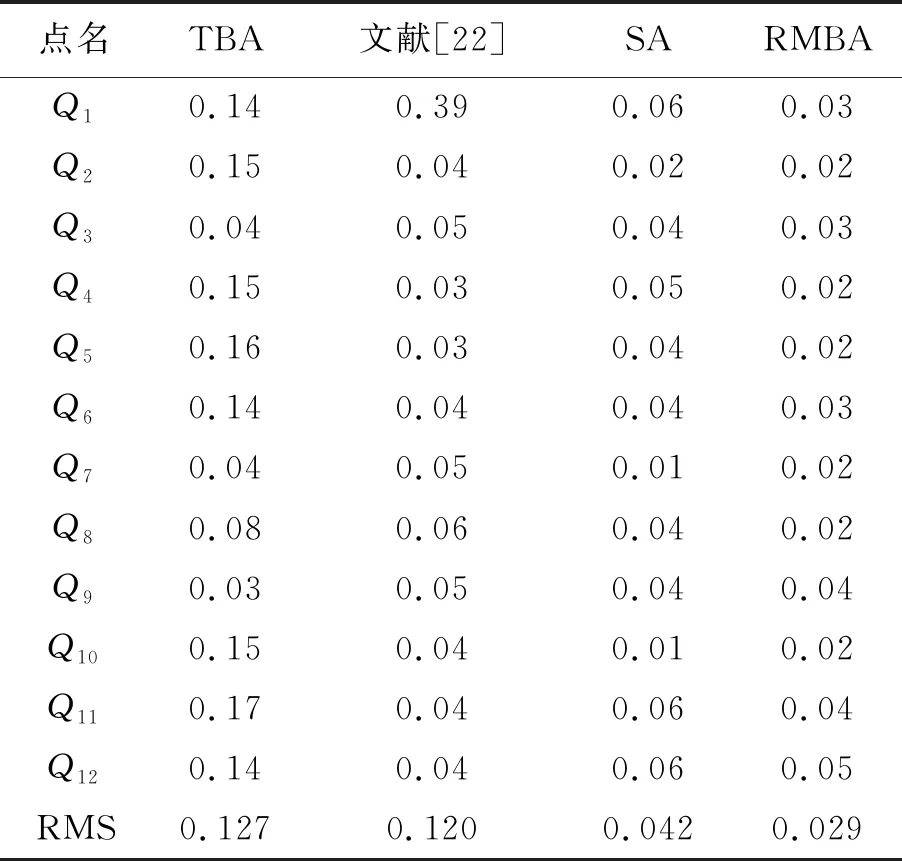
表4 控制点三维坐标偏差及均方根(含粗差)

对比表4和表2可知，在观测值中加入粗差后，TBA解算的控制点三维坐标偏差均方根由0.057 mm增大为0.127 mm，且所有点对应的三维坐标偏差均明显变大，表明粗差观测值影响了所有点坐标的解算结果。文献[22]方法解算的控制点三维坐标偏差均方根由0.057 mm增大为0.120 mm，与TBA结果不同的是，文献[22]结果中只有Q1点的三维坐标偏差明显变大，其余点的三维坐标偏差未受到明显影响。SA软件解算结果的坐标偏差均方根由0.041 mm变为0.042 mm，几乎未受到影响。RMBA方法的坐标偏差均方根由0.034 mm变为0.029 mm，与加入粗差前的结果相比甚至精度略有提高。分析其原因是，粗差对应的协方差和坐标值均未参与加权平均坐标的计算，相当于将第1测站照准Q1的所有观测值剔除，其计算结果有可能比原始观测值的计算结果更优。

为了进一步测试4种方法针对不同位置、不同大小、不同类型粗差的抗差性，设计了如下5组带有粗差的观测数据。

数据一：在模拟数据中，测站1照准Q1的测距观测值加上0.50 mm，将其改造为粗差观测值，其余观测数据不变。

数据二：在模拟数据中，测站1照准Q1、测站3照准Q8的测距观测值加上0.20 mm，将其改造为粗差观测值，其余观测数据不变。

数据三：在模拟数据中，测站1照准Q1、测站3照准Q8的测距观测值加上0.50 mm，将其改造为粗差观测值，其余观测数据不变。

数据四：在模拟数据中，测站1照准Q1的水平角观测值加上10″，将其改造为粗差观测值，其余观测数据不变。

数据五：在模拟数据中，测站1照准Q1、测站3照准Q8的水平角观测值加上10″，将其改造为粗差观测值，其余观测数据不变。

分别用四种方法处理这5组含有粗差的模拟观测数据，解算结果与设计坐标的三维坐标偏差均方根统计如表5所示。

由表5中数据一、数据二和数据三对应的结果可以看出，当观测值中含有测距粗差时，TBA和文献[22]方法的三维坐标偏差均方根与表2中的RMS相比明显变大；SA和RMBA的结果与表2中的RMS相比略有增大，但仍保持在同一量级。由数据四和数据五的结果可以看出，当观测值中含有测角粗差时，除了TBA外，其余3种方法的三维坐标偏差均方根无明显变化，分析其原因是由于该算例的测量范围较小，距离较近，由测角误差引起的点位偏差较小，导致平差结果对测角粗差不敏感。总的来看，TBA和文献[22]的抗差性较弱，SA软件与本文算法均能够有效抵抗粗差观测值的影响，解算精度与处理无粗差观测数据的精度基本保持在同一量级。

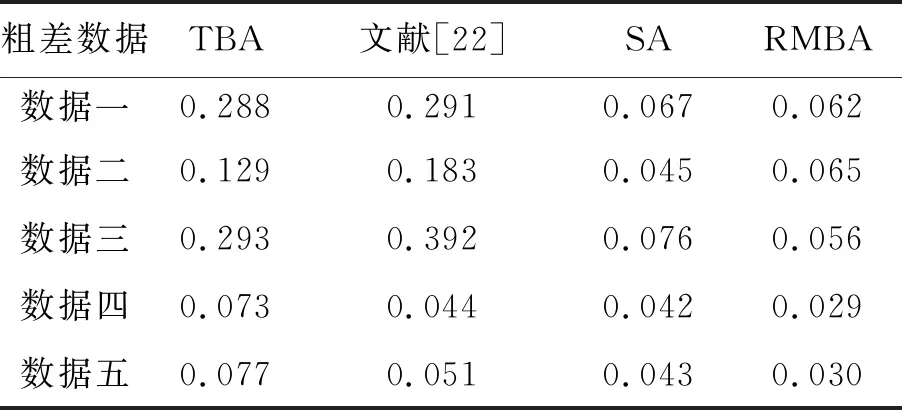
表5 5组粗差数据的三维坐标偏差均方根

3.2 实测数据试验

利用1台Leica AT402激光跟踪仪在上海光源实验大厅按自由设站法采集了4个测站的数据，共有42个控制点，测量场景如图3所示。图3中，点 5到点BD821的距离约为100 m。

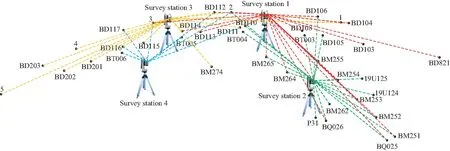
图3 实测数据试验测量场景示意图Fig.3 Schematic diagram of measurement situ of actual data experiment

SA软件经受了众多实践应用的考验，可以用其他方法的解算结果与SA的解算结果公共点转换后的点位偏差来评价其精度。分别用TBA、文献[22]方法、RMBA及SA软件处理这4个测站的实测数据，将4组平差结果转换至同一坐标系后，求TBA、文献[22]方法与RMBA解算的控制点坐标到SA解算的控制点坐标的偏差，结果统计情况如表6～表8所示。

已知SA软件处理这4个测站实测数据的点位中误差为0.05 mm，最大点位误差为0.21 mm。对比表6～表8可知，TBA解算的控制点坐标与SA解算的控制点坐标最大偏差达0.45 mm，三维坐标偏差均方根为0.24 mm，与SA结果的差异较大。文献[22]方法的计算结果与SA解算的控制点坐标最大偏差达0.21 mm，三维坐标偏差均方根为0.11 mm。RMBA解算的控制点坐标与SA解算的控制点坐标最大偏差为0.21 mm，三维坐标偏差均方根为0.07 mm，表明RMBA的平差结果与SA软件的平差结果在同一精度量级。

表6 TBA解算的坐标与SA解算坐标的偏差统计

表7 文献[22]方法解算的坐标与SA解算坐标的偏差统计

表8 RMBA解算的坐标与SA解算坐标的偏差统计

4 结 论

本文在传统激光跟踪仪多测站光束法(TBA)平差模型的基础上，通过引入马氏距离改造了平差准则，以“使观测值到加权平均值的马氏距离平方和最小”为平差准则，并在计算加权平均坐标时对粗差观测值进行剔除，构建了抗差马氏光束法(RMBA)平差模型。通过MATLAB仿真试验对比了TBA、文献[22]方法、SA软件和RMBA 4种模型的解算精度，结果表明RMBA解算结果的精度优于TBA、文献[22]方法和SA软件的解算精度，而且RMBA模型具有抗差性。利用Leica AT402激光跟踪仪在上海光源实验大厅100 m范围内的4个测站观测数据进行实测数据试验，分别用TBA、文献[22]方法和RMBA处理了数据，并与SA软件的平差结果进行了对比，结果表明RMBA的解算结果与SA软件的平差结果在同一精度量级。

不足之处是，仿真数据试验的网形结构较为单一，实测试验的测站数及控制点数还不够多。 下一步可开展更为丰富的仿真数据试验和实测试验，验证RMBA模型在处理不同网形结构、不同测量精度的数据时的性能。