动态磁场校准的九轴惯性融合

蔡浩原，赵晟霖，崔松叶，李文宽，刘春秀

(1.中国科学院 空天信息创新研究院 传感技术国家重点实验室，北京 100190；2.中国科学院大学，北京 100049；3.深圳前海维晟智能技术有限公司，广东 深圳 518101)

1 引 言

随着低成本、轻重量的微电子机械系统(Micro-Electro-Mechanical System，MEMS)的发展，更小、更便宜的惯性传感器被越来越广泛地应用，尤其是移动设备、游戏机等消费类电子产品。MEMS小尺寸、低载荷的特点还能够满足小型机器人和微型飞行器的要求，使自主导航和控制成为可能。但是，低成本MEMS输出的数据受到高水平噪声和时变偏差的影响，必须使用传感器融合算法对数据进行处理，以获得平滑且无偏差的方位估计[1]。

对于俯仰角和翻滚角，通过三轴陀螺仪和三轴加速度计的融合就可以获得准确且不随时间漂移的结果，但是由这种六轴融合算法解算的航向角会由于陀螺仪的积分误差无法补偿而随时间漂移。所以，确定准确的航向角需要用磁力计测量地球磁场作为绝对参考[2-5]，而磁力计的实际使用极易受到环境磁场的干扰，包括硬磁干扰和软磁干扰[6]。所以在低成本MEMS惯导领域，如何减小航向角随时间的漂移是最困难的问题，其关键就是如何实时地、便捷地校准磁力计。

对于磁场的校准，一种传统的方法是建立磁场模型，根据磁场数据的约束条件，仅利用磁力计本身的数据计算校准参数，最常用的是椭球拟合法[7-9]。椭球拟合在一般环境下能取得很好的校准效果，但对磁力计数据的要求很高，需要磁场数据点均匀地分布在椭球表面，实际使用中需要执行数据采集动作，比如使设备在空间中绕“8”字运动，这对用户非常不友好，而且在某些场景(如无人机、机器人)中很难实现。此外，椭球拟合法在磁力计使用环境发生变化后需要重新校准，所以它既不具备便捷性，也不具备实时性。

使用惯性器件辅助磁场传感器的校准是一个新的思路。Kok[10]将磁强计测量和惯性测量结合起来进行方位估计，将标定算法归结为最大似然问题，综合使用了椭球拟合和扩展卡尔曼滤波(Extended Kalman Filter，EKF)等算法，但它不能实时工作。Han Ke等[11]在忽略传感器轴定位误差和假定陀螺仪偏差为常值的条件下，使用EKF融合了陀螺仪和磁力计数据，实时计算了包括磁场向量、硬磁干扰和软磁干扰在内的磁场信息，但是由于EKF自身的特点，算法缺乏对突变状态的快速响应能力[12]。Zhu Maoran等[13]通过求解齐次最小二乘问题，提出了一种陀螺辅助磁力计的校准算法，该算法虽能够在一步内完成传感器的内禀标定和交叉标定，但其只能单独作为一种粗略的标定方法，或作为其他精细算法的良好初值，并不能实现实时校准。

姿态估计最常用的方法是扩展卡尔曼滤波(EKF)和互补滤波(Complementary Filter，CF)，而且大多数融合算法都是以四元数的形式进行方向估计的[1]。对于EKF，状态量数目的增加也会增加滤波方程的复杂程度，同时增加矩阵求逆的运算复杂度，从而对计算造成负担。当模型的线性化假设不成立时，EKF的线性化近似还会导致滤波器极度不稳定。而且在实际应用中，外界噪声也往往不符合高斯白噪声的假设[14]。因此，互补滤波常常成为EKF的替代方案，因为其无需任何统计描述，简单有效，收敛速度相比于EKF也更快[1]。互补滤波的代表性研究中[15-17]，Euston使用PI控制器调控向量积形式的误差[16]，Madgwick使用梯度下降法调控线性形式的误差[17]。这两种方法在低成本MEMS惯性传感器中应用十分广泛。

本文综合考虑各种磁场校准与姿态估计的方法，认为可以从算法上减小航向角的漂移而不必增加传感器的成本。为了实现动态的、更便捷的磁场校准，本文使用EKF融合惯性传感器(陀螺仪)和磁力计，同时考虑EKF失效的问题，对其校准的效果做出量化评价，以调整其在姿态估计中的作用程度。作用程度通过互补滤波中PI控制器的参数来体现，它是一个动态的函数，可以实时调整磁力计在融合算法中的比例。此外，为了进一步减小惯性测量单元(Inertial Measurement Unit，IMU)的误差，还要考虑自由加速度的影响，Hytti在卡尔曼滤波中通过干预测量矩阵协方差来减小有害加速度的影响[18]，本文使用更简单并且与磁力计统一的调整方法，同样定义其信赖函数，动态控制加速度在融合算法中的比例。

2 算法原理概述

2.1 算法原理概述

图1为本文算法的原理图。 首先在获取传感器数据阶段对陀螺仪进行校准，本文将陀螺仪的漂移误差认定为一个随机变量，通过监测陀螺仪在静止或匀速状态时的输出实时更新陀螺仪的漂移值，并在以后的测量值中减去。加速度计，容易受到高频噪声的干扰，因此在这个阶段还要对其进行低通滤波处理。EKF磁场校准单独作为一个阶段，使用陀螺仪辅助磁力计进行校准。在互补滤波中，本文分别对磁场信息和加速度信息定义信赖参数，并作用到PI控制器中，进一步减小由于实际运动环境引起的误差。

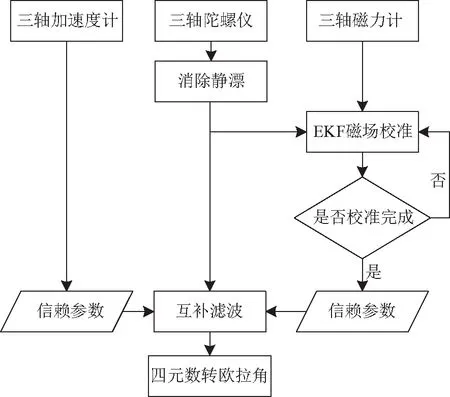
图1 算法原理图Fig.1 Block diagram of the algorithm

2.2 EKF动态磁场校准

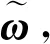
(1)

(2)

bg，k=(1-β)bg，k+βbg，k-1.

(3)

(4)

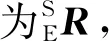
(5)

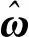
(6)

综上易得：

(7)

式(7)表示，通过上一时刻的磁场准确值和陀螺仪准确值，可以先验地预测出当前时刻的磁场准确值，这也是EKF中状态预测的关键步骤。把磁场校准值、硬磁干扰矩阵、软磁干扰矩阵组合为状态量，就可以推导出全部的滤波方程。其中，由于测量方程是公式(4)，它对于状态量来说是非线性的，所以要对其泰勒展开保留一阶项，使用EKF完成校准。

2.3 互补滤波

本文的互补滤波系统框图如图2和图3所示。

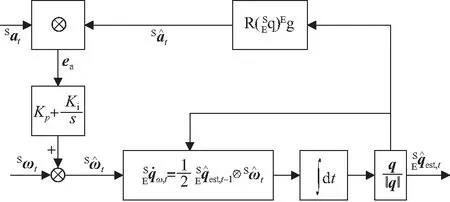
图2 六轴融合原理图Fig.2 Block diagram of six-axis fusion

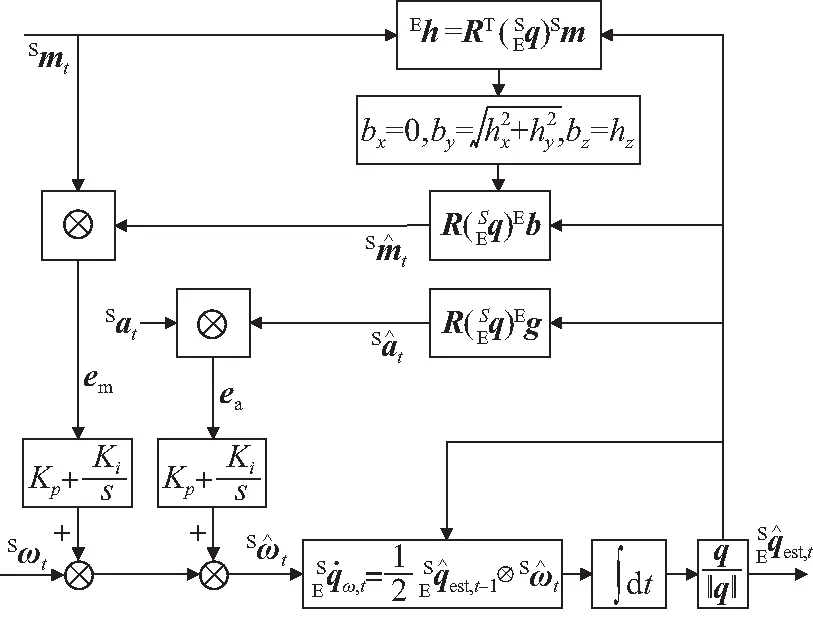
图3 九轴融合原理图Fig.3 Block diagram of nine-axis fusion

图2的六轴融合算法使用IMU，把加速度测量值和理论值做外积得到控制误差，图3的九轴融合算法加入了磁力计，把磁力计测量值和理论值的外积作为另一项控制误差。关于互补滤波的原理，文献[15-17]已经做了详细描述，此处不再赘述。图3中，为了分别定义加速度计和磁力计的信赖参数，使用了两个不同参数的PI控制器，这是对Euston[16]方法的改进。

3 信赖参数

3.1 加速度的信赖参数

无论是互补滤波还是卡尔曼滤波，都是把竖直向下的重力加速度作为一个绝对参考，所以非重力自由加速度是影响结果准确性的关键误差来源。对于这个问题，Hytti修改了EKF的测量噪声协方差矩阵，形式上把加速度计的测量作为了加速度计噪声方差的权[18]。这样，当加速度测量激增时，测量噪声也会随之激增，从而可以调整卡尔曼增益，达到自适应的目的，但可能面临参数调节的问题。本文参考这样的思路，在更简单的互补滤波器中修改Pl控制器的比例环节，给其赋予自适应性。

首先考虑3种情况：

(1)静止或匀速状态，加速度计只有重力加速度作用，测量信息可以完全信赖。

(2)低加速度状态，此时出现了非重力加速度的干扰，但影响并不大，应该使算法适当减少对加速度计测量的依赖。

(3)高加速状态，这是最大的误差来源，应该使对加速度计的依赖无限减小，当非重力加速度极大时甚至可以使其趋近于0。

对于这些情况，陈亮[14]给出的方法是对这3种状态使用分段函数，对每一段进行实验测试确定最佳参数。但是这种方法不仅需要分3段测试，还需要确定区分3种状态的阈值，实际操作起来非常困难。本文直接使用一个指数函数来模拟上述过程。设加速度计的信赖参数为ξa，加速度向量为a，当地的重力加速度大小为G，k时刻加速度的大小与G的差为δk，即：

δk=abs(‖ak‖-G).

(8)

那么，信赖参数可以定义为：

ξa，k=exp(-λaδk)，

(9)

其中λa是一系数，如图4所示，当λa=2时ξa的图形。可以直观地看出，指数函数的形状符合对加速度计信赖程度动态调整的过程，加速度测量值越接近G，加速度越可信赖；测量值越偏离G，加速度的信赖参数越小，且当偏差过大时趋近于0。

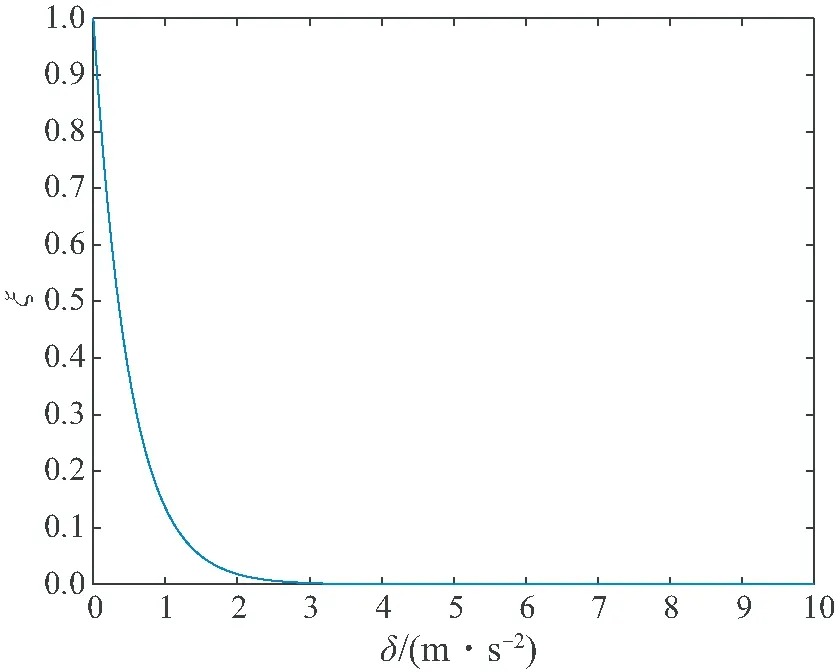
图4 信赖参数ξ随δ变化曲线Fig.4 Curve of ξ varies with δ

设Kp，0为比例常数初始值，则修正后的比例环节为：

Kp=Kp，0ξ.

(10)

3.2 磁场向量的信赖参数

对于磁场校准的过程有两点需要考虑，第一是算法开启时的收敛过程，第二是校准完成后滤波器的抗突变能力。EKF的校准过程虽然不像椭球拟合一样严格，但是也要求算法能足够地适应磁场环境，那么收敛速度就会与使用状态有关。在算法开启时一般不直接使用EKF输出的信息，而是监测校准后的磁场强度，使用一个滑动窗口向后取固定长度的数据段，计算其均方根误差(Root Mean Squared Error，RMSE)，当RMSE少于一个阈值并稳定时，就认为磁场已校准完毕，可以开始使用磁场数据进行九轴融合。

(11)

4 实验与结果

4.1 实验设备

本文使用的采集设备是广州阿路比电子科技有限公司的LPMS-B2，如图5所示，它是一种微型无线惯性测量单元(IMU)/姿态航向参考系统(Attitude and Heading Reference System，AHRS)，表1为LPMS-B2与本文相关的技术参数。在本文的实验中，传感器的采样率均为100 Hz。

图5 LPMS-B2九轴模块Fig.5 Photograph of LPMS-B2

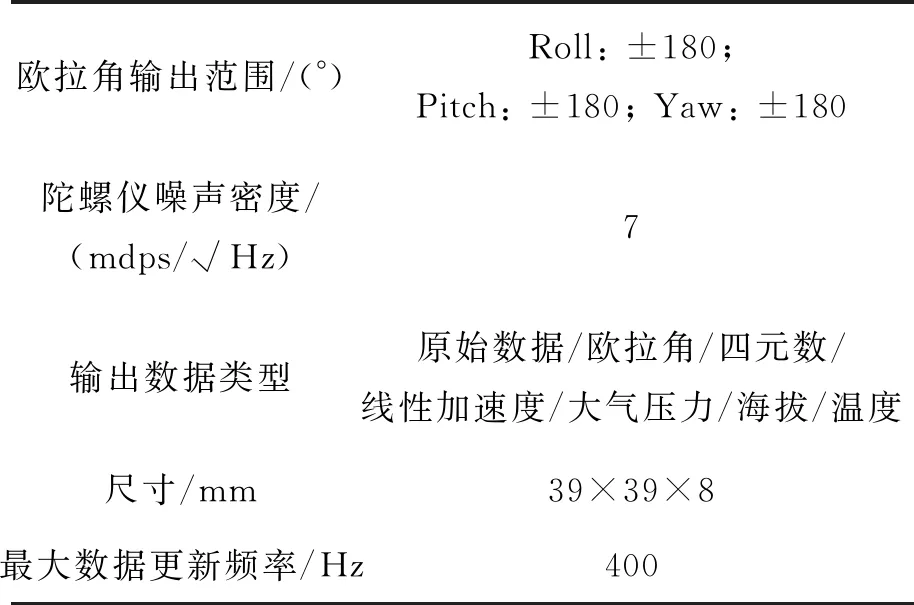
表1 LPMS-B2技术参数

4.2 EKF磁场校准实验

考察EKF校准与椭球拟合校准在软磁、硬磁干扰下的校准效果。用来对比的椭球拟合算法是十分量椭球拟合算法，这种算法效果较好，但运算量较大。LPMS-B2模块输出的原始磁力计数据已经包含了较大的硬磁干扰，还需要在模块上绑一把钥匙来作为软磁干扰。将模块在空中晃动约5 s，把EKF最终迭代得到的磁场向量作为真实值，则其模值即为理想磁场球体的半径长度。把原始磁场数据、椭球拟合校准的磁场数据、EKF校准的磁场数据分别拟合成球体，如图6所示，可以直观地观察3种数据的质量，拟合的球体越圆、球体半径越接近真实地磁场强度、球体球心越接近原点，数据的质量越好。

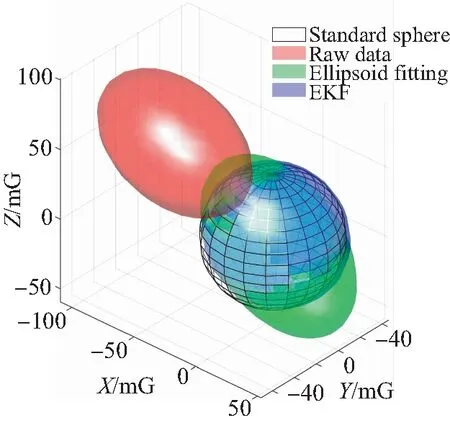
图6 存在软磁干扰、硬磁干扰的磁场校准实验Fig.6 Calibration experiment of magnetic field with soft and hard magnetic interference

从图6可以直观地得出结论，椭球拟合和EKF都能对硬磁干扰起到校准效果，但是椭球拟合对软磁干扰的校准效果非常有限，而EKF可以较好地处理软磁干扰。取图6中每个椭球上的点与坐标原点的距离与理想球体的差，得到关于校准效果的误差曲线，如图7所示。可以看出，EKF和椭球拟合的误差曲线与零线较近，这是因为两种算法对硬磁干扰都起到了校准作用，而EKF误差曲线更平滑，说明EKF对软磁干扰的校准效果更好。

图7 三个椭球与标准球体表面的距离曲线Fig.7 Curves of the distance between ellipsoids and standard sphere

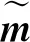
(12)

另需要指出，椭球拟合算法对采样有要求，在数据不够时无法完成校准，文献[19]对此进行了演示。因此，在实际应用的意义上椭球拟合的校准速度是不确定的，如果采样满足要求，则椭球拟合算法收敛部分的曲线斜率与EKF相仿。

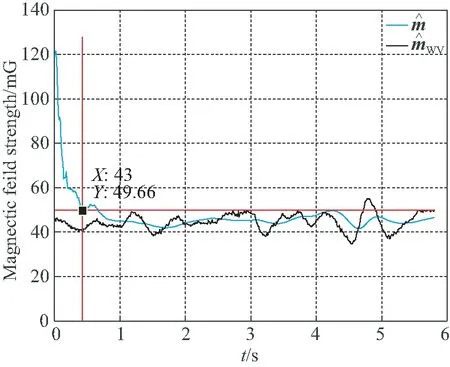
图8 磁场滤波值与真值随时间变化曲线Fig.8 Time varying curves of filtered magnetic field value and true value

4.3 九轴融合姿态解算实验

本节考察本文的融合算法与LPMS-B2的九轴融合算法在短时间内的计算结果有何差异。将模块拿起在空中摇晃片刻，然后将记录的传感器原始数据输入MATLAB计算，画出MATLAB计算的姿态角和LPMS-B2输出的姿态角，如图9所示，尾标1表示本文算法，2表示LPMS-B2。

由图9看出，在短时间内，两种算法计算出的欧拉角并无太大差异。

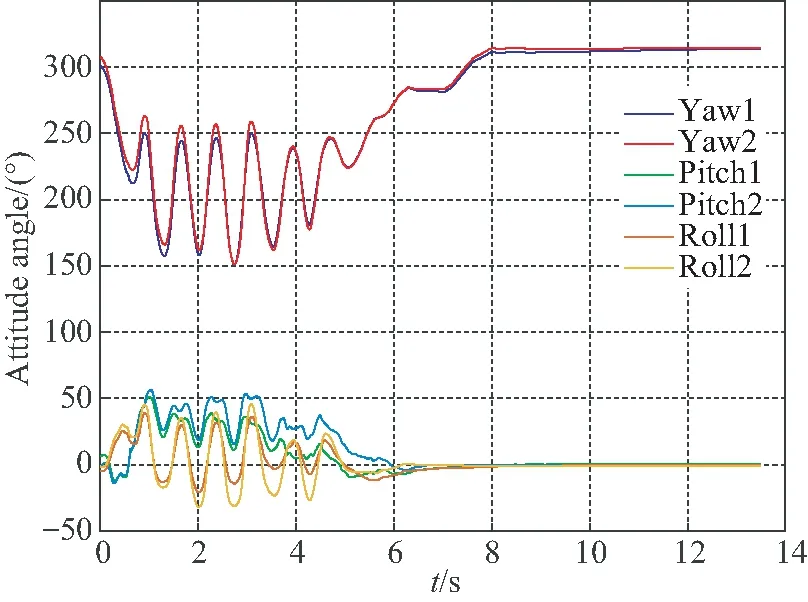
图9 本文的融合算法与LPMS-B2融合算法的姿态角结果

4.4 与LPMS-B2内置滤波器的航向角对比实验

LPMS-B2内置的姿态角解算算法是卡尔曼滤波，包括六轴、九轴的卡尔曼滤波和磁场校准。本节考察本文算法的航向角漂移在相同的设备上是不是更小，具体实验步骤为：

(1)将模块按抵在桌面上的参考线边缘，开启模块，与电脑蓝牙连接，选择一种滤波器(六轴或九轴卡尔曼滤波)和输出的数据类型，点击按钮开始记录。

(2)将模块拿起随意转动5 s作为校准阶段，然后放回抵住参考线，将此时作为t0时刻。

(3)滑出模块，贴住桌面顺时针旋转3圈放回，停顿一段时间。

(4)连续重复步骤3，持续10 min左右。

(5)关闭记录数据按钮，结束实验。

实验场景如图10所示。

图10 实验场景Fig.10 Scene of the experiment

4.4.1 与LPMS-B2的六轴算法作比较

选择gyr+acc(Kalman)滤波器，记录其欧拉角输出和九轴传感器的原始数据，得到的数据集为LPMSB2_3.csv，总时长615 s，约为10 min，共顺时针旋转了105圈。取数据集的第2 640～3 470行作为初始段，比较之后的停靠过程与此段航向角的偏差，偏差曲线由图11给出。为了便于读者阅读，图11对纵轴做了截断，只绘出了-10°～30°的部分。蓝色线为本文九轴算法的结果偏差，可读出每次停靠后航向角与初始的偏差都很小；红色线为LPMS模块的六轴计算结果偏差，偏差呈增大趋势(彩图见期刊电子版)。具体数值见表2。

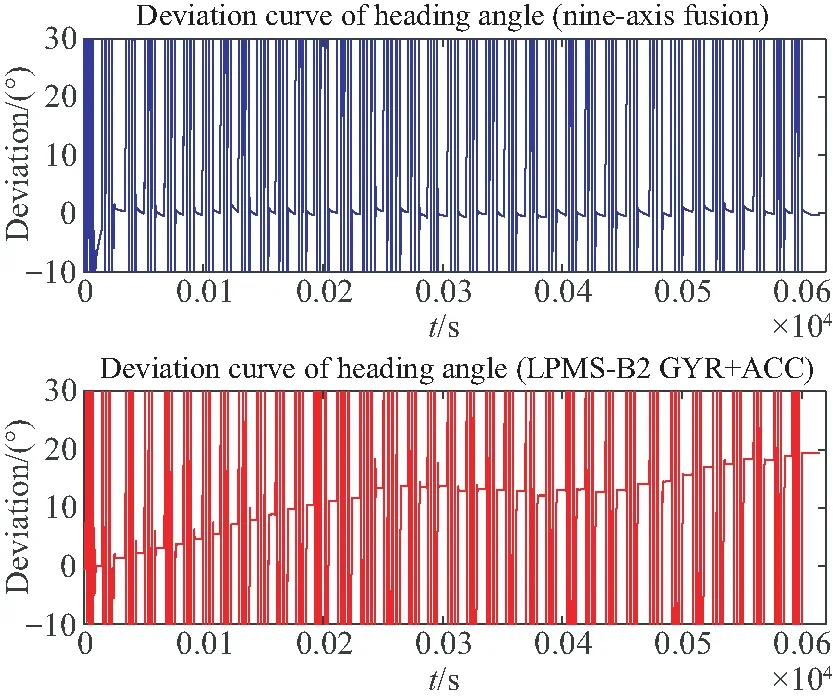
图11 本文九轴算法与LPMS-B2六轴算法的航向角偏差

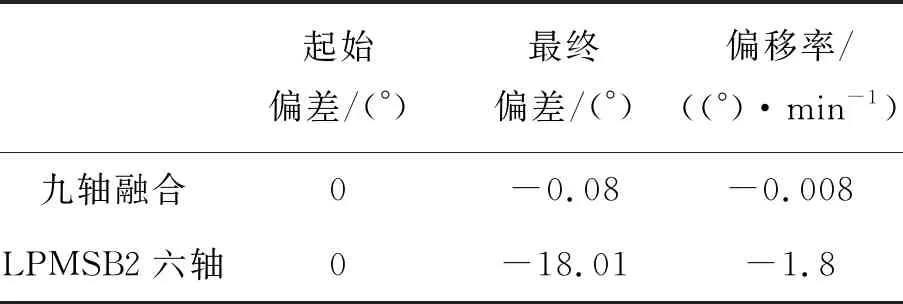
表2 航向角偏差对比1

由表2，LPMS-B2模块的六轴算法在连续的旋转运动中也会出现比较大的误差，偏差率为-1.8 (°)/min，而本九轴算法在此次实验中的偏差率为-0.008 (°)/min，几乎做到了不偏。

4.4.2 与LPMS-B2的九轴算法作比较

选择gyr+acc+mag(Kalman)滤波器，记录其欧拉角输出和九轴传感器的原始数据，得到数据集LPMSB2_5.csv，总时长670 s，约11 min，共顺时针旋转了117圈。取数据集的第3 500～4 500行作为初始段，比较之后的停靠过程与此段航向角的偏差，偏差曲线由图12给出(彩图见期刊电子版)，纵轴同样做了截断处理。蓝色线为本文九轴算法的结果偏差，性质与上一个实验相同；红色线为LPMS模块的九轴计算结果偏差，同样呈增大趋势。具体数值见表3。

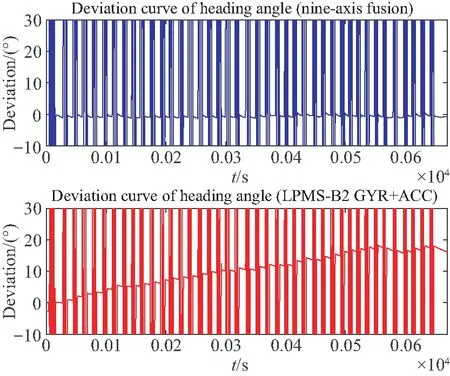
图12 本文九轴算法与LPMS-B2九轴算法的航向角偏差

由表3，在连续的旋转运动中，LPMS-B2模块的九轴算法航向角的偏差率为-1.39 (°)/min，与六轴的-1.8 (°)/min相比有所减小但不显著；本文的九轴算法在此次实验中的偏差率为-0.038 (°)/min，仍然远小于模块算法的偏差率。

表3 航向角偏差对比2

4.5 运算量分析

从磁场校准和姿态解算两个部分分析算法运算量。对于椭球拟合算法，计算最复杂的部分的是矩阵求逆运算，矩阵求逆的算法复杂度是O(n3)，即复杂度随矩阵阶数n呈指数增长。十分量椭球拟合需要计算10阶方阵的逆，朱建良[7]的椭球拟合算法需要计算6阶方阵的逆，EKF磁场校准中需要求逆的矩阵只是3阶的方阵，再加上其他的矩阵乘法运算需要的乘法数，与椭球拟合算法总体的乘法数相差不大。在姿态解算的方法中，互补滤波法除矢量外积外不涉及矩阵运算，比卡尔曼滤波有公认的计算速度和收敛速度上的优势[1]。

算法实际测试使用的MCU为主频为180 MHz的STM32F427AG(1 024 K Flash，256 kB SRAM)，实际程序占用空间为90 kB(FLASH)，运行占用空间为25 kB(RAM)，每次迭代用时为16.4 ms，约每秒60帧运算。因此，根据4.2节对EKF磁场校准收敛速度的分析，算法在1 s内就可以完成校准，即时参与航向角的校正。

5 讨 论

本文的EKF磁场校准，可以做到实时和动态，并且当磁场数据点不佳的情况下也能起到校准效果，与椭球拟合相比，还很好地补偿了软磁干扰。但是本文磁场校准的缺点是难以快速响应突变的磁场环境，这是因为稳定状态下滤波器的最佳增益矩阵不会随着残差的增大而增大。本文的处理方式是，当发生这种干扰过大的情况而导致校准后的磁场强度偏离正常值(55±10) mG太多时，就减小对磁场信息的信任程度，使其趋近于0，当磁场强度恢复到正常范围内后再重新增加对磁场信息的信任程度，但在此过程中还是会累积航向角误差。

本文的航向角输出非常稳定，在10 min的连续旋转运动中，漂移仅为-0.08°和-0.42°，与商用的惯导模块LPMS-B2相比几乎是无偏的。但存在一个问题，由于EKF磁场校准的收敛速度相比于互补滤波器慢，所以在算法开启的一小段时间内航向角并没有迅速达到稳定。所以，本文下一步的研究是如何加快EKF的收敛速度与跟踪能力。

6 结 论

本文研究了两个问题，第一是在使用MEMS传感器解算姿态时，航向角随时间偏移逐渐增大的问题，第二是传统的椭球拟合磁场校准方法缺乏校准的实时性和便利性，以及难以应对软磁干扰的问题。第二个问题的解决是第一个问题解决的关键。因此，本文使用了一种基于EKF的动态磁场校准方法，通过旋转矩阵建立陀螺仪与磁力计的关系，把测量方程的元素同样作为状态量进行预测更新，实现了兼具实时性和便利性的动态磁场校准。实验结果表明，本文的EKF磁场校准方法能有效改善椭球拟合算法对校准数据要求高的缺点，并且能很好地消除软磁干扰的影响。在这个基础上，本文在互补滤波中着重考虑了自由加速度和磁场环境突变的情况，定义了各自的信赖函数，对PI控制器做了修改，使其对加速度和磁场的突变具有自适应能力，基本消除了自由加速度和畸变磁场对姿态角解算的影响。实验结果表明，当传感器采样率为100 Hz、运行时长约为11 min、旋转圈数约为117圈时，本文算法航向角的漂移为0.42°，与对比的商用惯导模块算法相比减小了14.9°，性能实现了数量级的提升。

本文提出的方法在控制减小航向角漂移上有较大的优势，并且同时满足校准便捷、适用场景多样等要求，在低成本MEMS惯性导航领域有广阔的应用前景和极大的研究潜力。如何加强抗强磁场干扰的能力，以及如何改进滤波器、加快恢复收敛的速度是下一步研究的重点。