液体粘滞阻尼器减震结构功率谱密度分析方法
陈夏楠, 张令心, 陈永祁, 朱柏洁
(1.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080;2.北京奇太振控科技发展有限公司,北京 100037)
近年来,消能减震技术在结构抗震中的应用日益广泛。消能减震结构的地震反应分析方法目前主要有2种,其中最常用的一种方法是时程分析法[1-3],但该方法计算量较大,计算结果易受地震动时程选取的影响;另一种方法是计算量相对较小的振型分解反应谱法,对于该方法,目前常用的结构有限元软件可以将阻尼元件附加给结构的阻尼转换成为振型阻尼比进行计算,但上述对附加阻尼的处理方法使得结构分析过程不能考虑模态耦合的完全阻尼[4]。功率谱密度分析方法采用地震动的功率谱密度函数作为地震激励,而功率谱密度函数包含了随机地震荷载的统计特征,因此可以弥补上述方法的不足。虚拟激励法[5-6]是功率谱密度分析方法在土木工程领域运用较多的方法,但由于物理概念相对复杂,该方法在实际工程结构的减震计算分析中应用较少。针对以上问题,本文提出一种基于功率谱密度函数的附加液体粘滞阻尼器结构地震反应分析方法,并进一步结合结构最大地震反应的概率估计方法提出了该类型结构的地震可靠度分析方法,且该方法可通过实际工程结构分析中广泛使用的通用有限元软件SAP2000得以实现。利用算例对比该方法与时程分析法、振型分解反应谱法的计算结果,并采用该方法进行附加液体粘滞阻尼器结构的地震可靠度分析。
1 基于功率谱密度附加液体粘滞阻尼器结构地震反应及可靠度分析方法
功率谱密度函数可以完整反映规范设计反应谱的统计特征,相比随机抽样得到的地震动时程曲线,它在统计意义上与规范设计反应谱更为接近。本文根据《建筑抗震设计规范》[7]中的设计反应谱求出相应的功率谱密度函数曲线,并确定了结构的阻尼,估算出结构在地震作用下最大反应的概率,并采用结构有限元分析软件SAP2000实现了附加液体粘滞阻尼器结构的地震反应及可靠度分析。
1.1 功率谱密度分析方法及参数选取
1.1.1 功率谱密度分析方法概述
本节通过时域分析与频域分析之间的转化关系,介绍结构频域内分析的运动方程以及功率谱密度分析的过程。假定x(t)为结构的位移时程函数,xg(t)为地面位移时程函数,在时域内,结构地震反应为[4]:
(1)
式中:M、C、K分别为结构质量矩阵、阻尼矩阵和刚度矩阵;Ceq为液体粘滞阻尼器等效线性阻尼系数矩阵。其中:
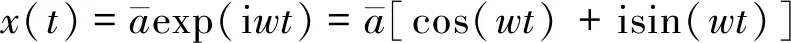

(2)
式(2)即为频域内结构地震反应的运动方程。
在SAP2000中,当使用功率谱密度分析方法时,运动方程右侧采用的输入荷载形式为[4]:
(3)
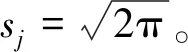
经过功率谱密度分析,可以得到结构对应不同频率点的地震反应。
1.1.2 功率谱密度函数的选取
由于目前振型分解反应谱法为主流的结构设计方法,因此,求出对应规范[7]设计反应谱的功率谱密度函数对结构设计十分重要。拟合功率谱密度函数的方法主要有2种:一种为迭代法[8-11],另一种是用概率的方法推导出地面加速度功率谱与结构最大加速度反应谱之间的近似关系[12]。
对于迭代的方法,在迭代出一组满足误差要求的谱值之后,通常会用最小二乘法将其拟合为金井清谱的谱参数,即将数据拟合为过滤白噪声模型来模拟地震动的功率谱密度分布[13]。本文采用了文献[13]选用柱修力-陈厚群功率谱的修正过滤白噪声模型,所选用的功率谱密度函数为:
(4)
式中:D、ω0、ξg、S0分别代表高频拐角周期、低频拐角频率、场地特征周期和谱强度。
1.1.3 阻尼的定义
结构的阻尼通常来源于2部分,一部分是作为整体应用到整个结构的阻尼,为方便计算,它常被分解为刚度比例阻尼和质量比例阻尼;另一部分为附加阻尼元件的阻尼。在时域内阻尼力F为:
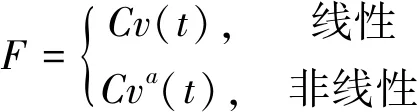
(5)
式中:C为阻尼系数;α为速度指数;v(t)为相对速度。而在频域内,由于SAP2000不能进行速度非线性的分析,因此需要首先根据耗能相等的原则,计算出等效线性阻尼。在SAP2000中,对于线性阻尼,程序可自动指定频域内滞回阻尼D(ω)为ωC[4]。
1.2 结构地震作用下最大反应的概率估计
功率谱密度函数描述了随机振动在频域内的统计特征,而结构反应在时域内达到某个特定值的概率是与功率谱密度函数在频域内的统计特征紧密相关的。因此,根据功率谱密度分析得到的结构反应的谱密度函数,可以求出该反应的均方根等统计参数,利用这些统计参数可以估算出结构反应的概率。达文波特[8]给出了随机振动中,结构反应y的绝对值在(0,Td)时段内不超过a的概率:
(6)
式中:
r=a/σy
(7)
(8)
(9)
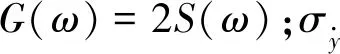
1.3 基于功率谱密度的附加液体粘滞阻尼器结构地震反应及可靠度分析在SAP2000中的实现
采用SAP2000进行附加液体粘滞阻尼器结构地震反应及可靠度分析的主要流程为:
1)建立结构有限元模型;
2)定义线性粘滞阻尼器及其参数;
3)定义功率谱密度函数及功率谱密度分析工况;
4)运行分析,保存结果,主要结果包括结构及阻尼器地震反应的频率-谱强度曲线,以及反应均值;
5)根据1.2节的公式计算结构及阻尼器的地震反应不超过某一特定值的概率。
2 三种结构地震反应计算方法对比
本文对附加液体粘滞阻尼器的结构分别采用振型分解反应谱法、功率谱密度分析法以及线性时程分析法计算其地震反应,对3种方法的计算结果进行对比。
2.1 结构有限元模型
选取一栋13层框架-剪力墙结构,结构平面图如图1(a)所示;结构平面柱距6 m,层高3.2 m,墙、柱混凝土强度等级为C40,梁板混凝土强度等级为C30,柱截面700 mm×700 mm,梁截面300 mm×600 mm,楼板厚120 mm,剪力墙厚200 mm,楼板所加恒载和活载均为3 kN/m2。利用SAP2000建立该结构的有限元模型,见图1(b)。模型中框架梁、柱采用杆单元;剪力墙采用薄壳单元;楼板采用膜单元,只起到传导竖向荷载的作用。
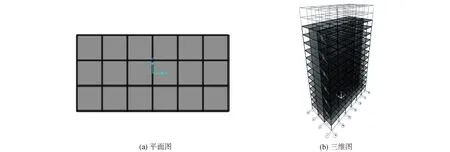
图1 算例1有限元模型Fig.1 Finite element model of example 1
为了对比3种方法对于阻尼器减震效果的计算结果,本文设计了3个结构模型,分别为无阻尼器结构、有阻尼器且阻尼系数C为1 000 kN/(m·s-1)的结构(以下简称附加阻尼器结构1)、有阻尼器且阻尼系数C为3 000 kN/(m·s-1)的结构(以下简称附加阻尼器结构2。阻尼器仅沿Y向布置,布置在结构剪力墙的2侧,与剪力墙在一条直线上,每层4个,隔层布置,共布置24个。定义结构自身阻尼比为0.05。
2.2 地震荷载
结构所在场地位于我国东部地区,抗震设防烈度Ⅷ度(0.2g),场地类别为Ⅱ类,地震分组为第一组,根据文献[13],式(4)中的高频拐角周期D与地震震级有关,首先根据设防烈度和地震分组,查表得到该场地震级相关参数M为6.26,再根据文献[14]表6地震震级与D值的关系,用插值法求高频拐角周期D为:
D=0.01492
(10)
低频拐角频率ω0为:
ω0=2πβ/3r=2π×3.5/(3×4)=1.832 59
(11)
杜修力等[15]指出可忽略震级对等效圆盘半径r的影响,直接将r取为4 km,由此计算得到ω0的值,如式(11)所示。最后根据文献[13]总结得出的不同设防烈度、场地类别以及地震分组所对应的场地土阻尼比ξg、卓越角频率ξg以及谱强度因子S0分别为0.726、18.05、58.99。
将以上各参数代入式(4),得到场地地面加速度的功率谱密度函数曲线如图2所示。
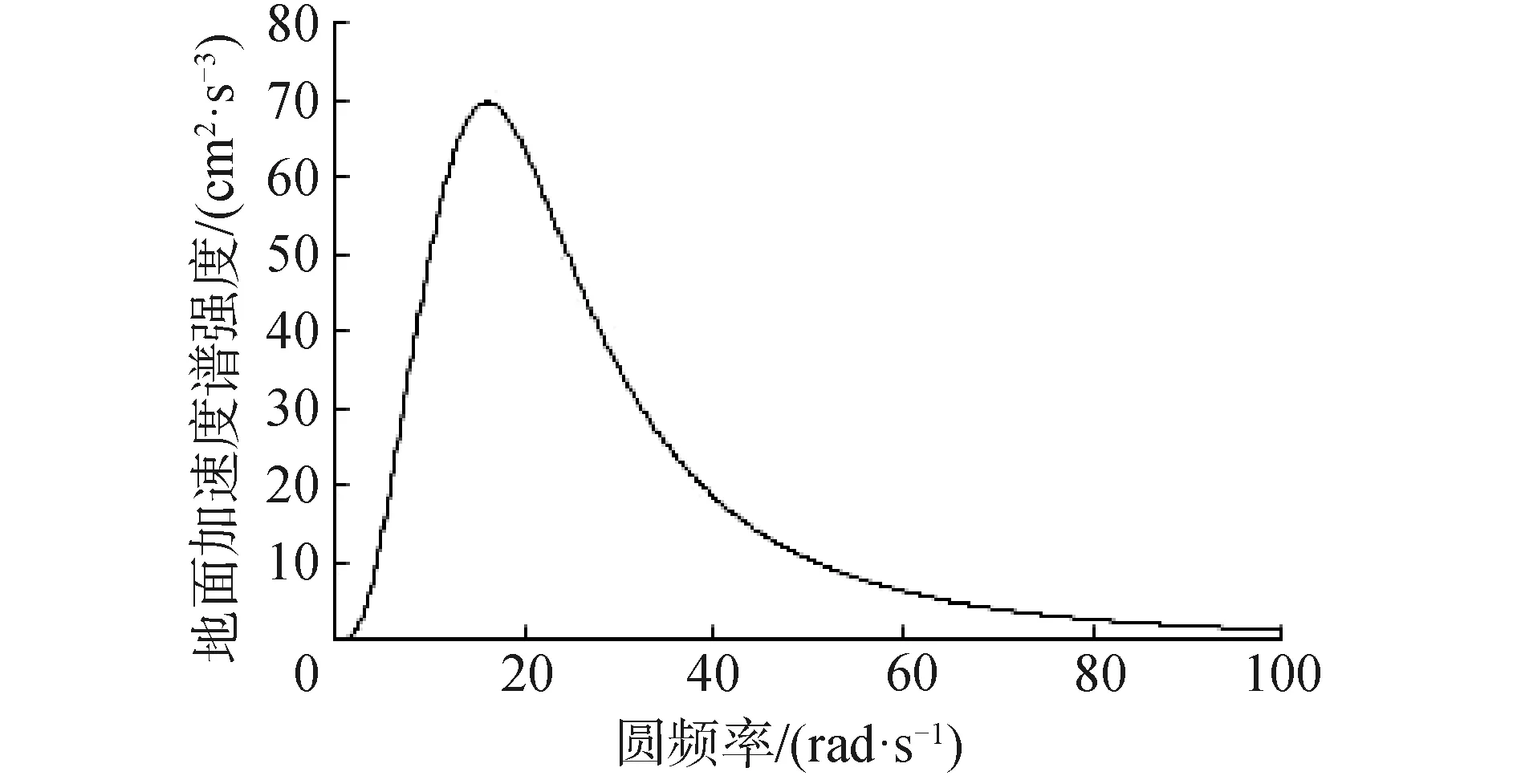
图2 地面加速度功率谱密度函数曲线Fig.2 PSD function curve of the ground acceleration
2.3 计算结果分析
对每组结构分别采用振型分解反应谱法、功率
谱密度分析法和直接积分的线性时程分析法进行Ⅷ度小震作用下的计算分析,其中线性时程分析所采用的地震动为根据《建筑抗震设计规范》[7]中的设计反应谱生成的10条人造地震动。人造地震动的反应谱与规范反应谱见图3。结构基底剪力的计算结果如表1所示。
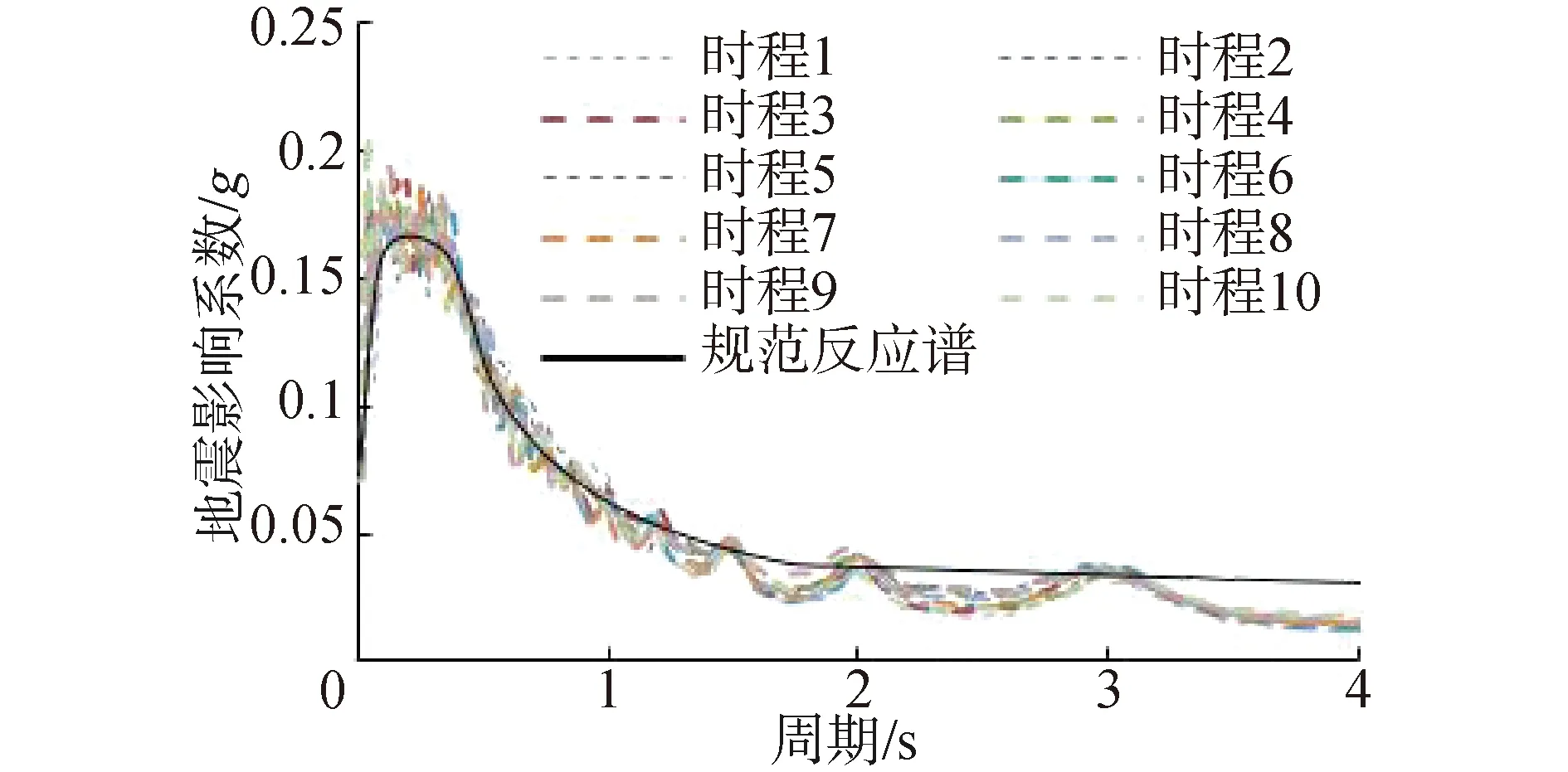
图3 规范反应谱与人造地震动反应谱Fig.3 Response spectrum curves of design ground motion and artificial ground motion
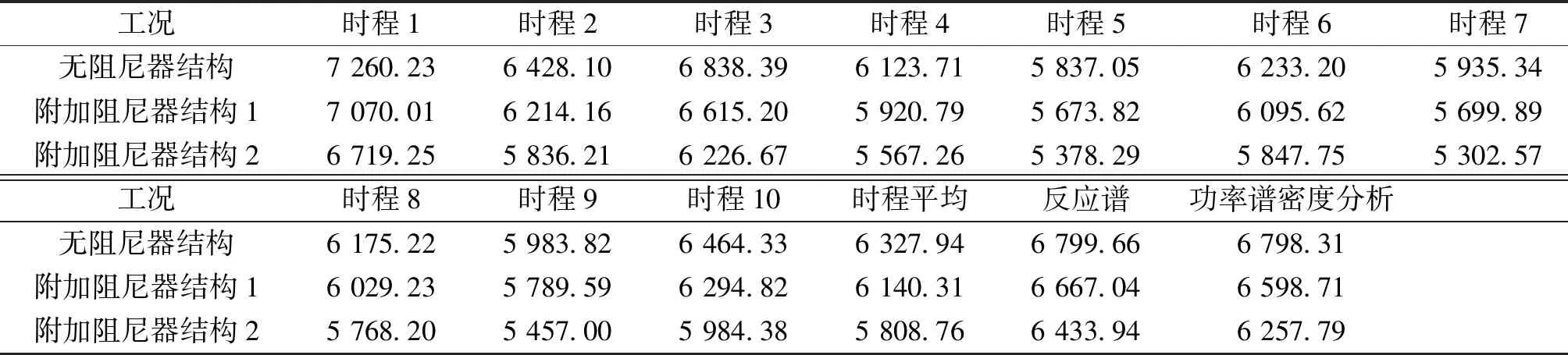
表1 3个结构的基底剪力计算结果Table 1 Base shear of 3 structures kN
直接积分的线性时程分析因适用性较广,在附加液体粘滞阻尼器结构的地震反应分析中,其结果常被作为对比验证值。采用振型分解反应谱法和功率谱密度分析法得到的计算结果与线性时程分析法得到的平均值的误差对比,见表2。其中误差的计算方式为振型分解反应谱或功率谱密度分析计算结果与时程分析计算结果差的绝对值除以时程分析计算结果。从表中可以看出,功率谱密度分析法与时程分析法的计算结果更为接近。
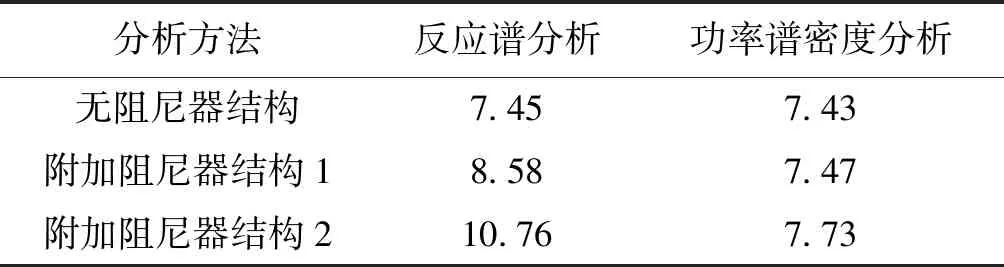
表2 振型分解反应谱法与功率谱密度分析法较时程分析法误差对比
表3为不同方法计算的各模型附加阻尼器后基底剪力减小的百分比,从表中可以看出,功率谱密度分析与直接积分的线性时程分析结果更加接近。

表3 结构基底剪力减小百分比Table 3 Decrease percentage of structural base shear %
通过上述结果对比可以看出,功率谱密度分析法计算的精度可以满足工程需要,该方法适用于附加液体粘滞阻尼器结构的地震反应分析。
3 基于功率谱密度的结构地震反应及可靠度分析方法应用算例
本节以实际工程结构模型作为分析对象,对使用非线性液体粘滞阻尼器减震前后的结构地震可靠度进行计算分析。
3.1 模型简介
该结构为位于新疆地区的23层框架-剪力墙结构,结构主体地下2层,地上23层,地下2~地上4层,层高4.5 m,平面尺寸30 m×55 m,其余各层层高3 m,平面尺寸30 m×35 m,结构主体总高75 m。标准层结构平面图见图4(a)。该工程所在场地抗震设防烈度为Ⅷ度(0.3 g),场地类别为Ⅱ类,地震分组为第3组。
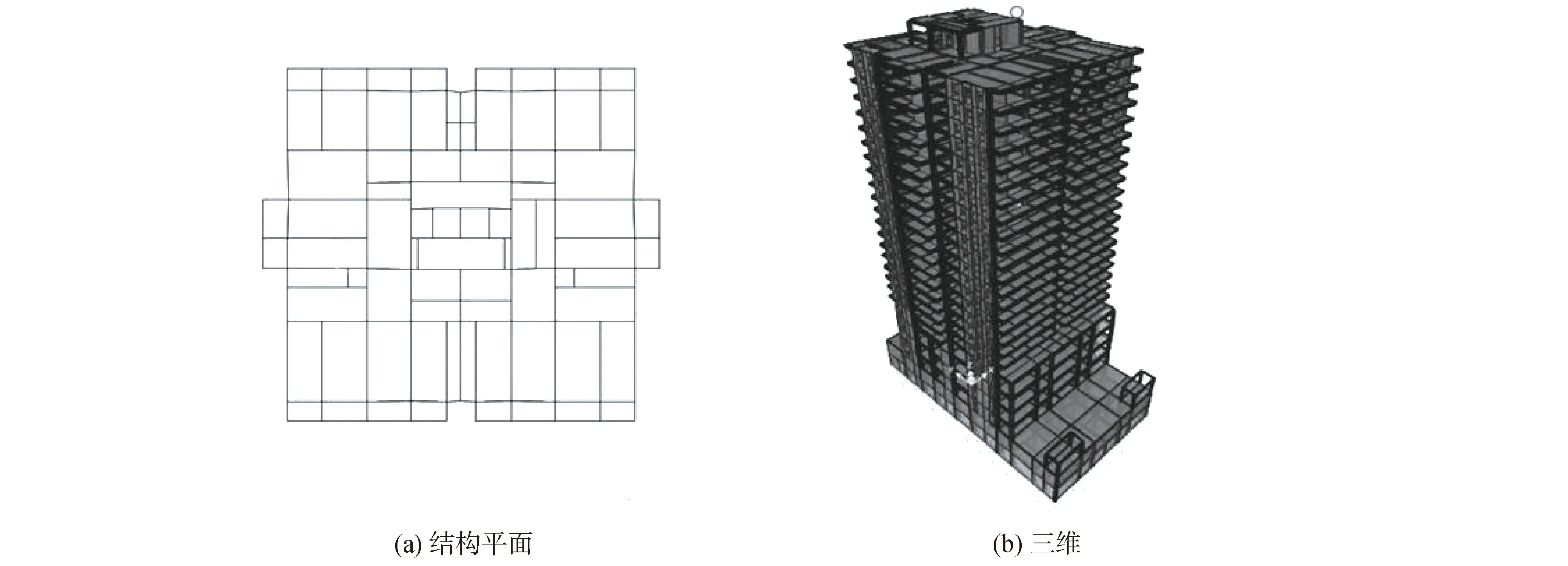
图4 算例2有限元模型Fig.4 Finite element model of example 2
根据前文方法选取对应场地的设计地震动功率谱密度函数曲线,如图5所示。
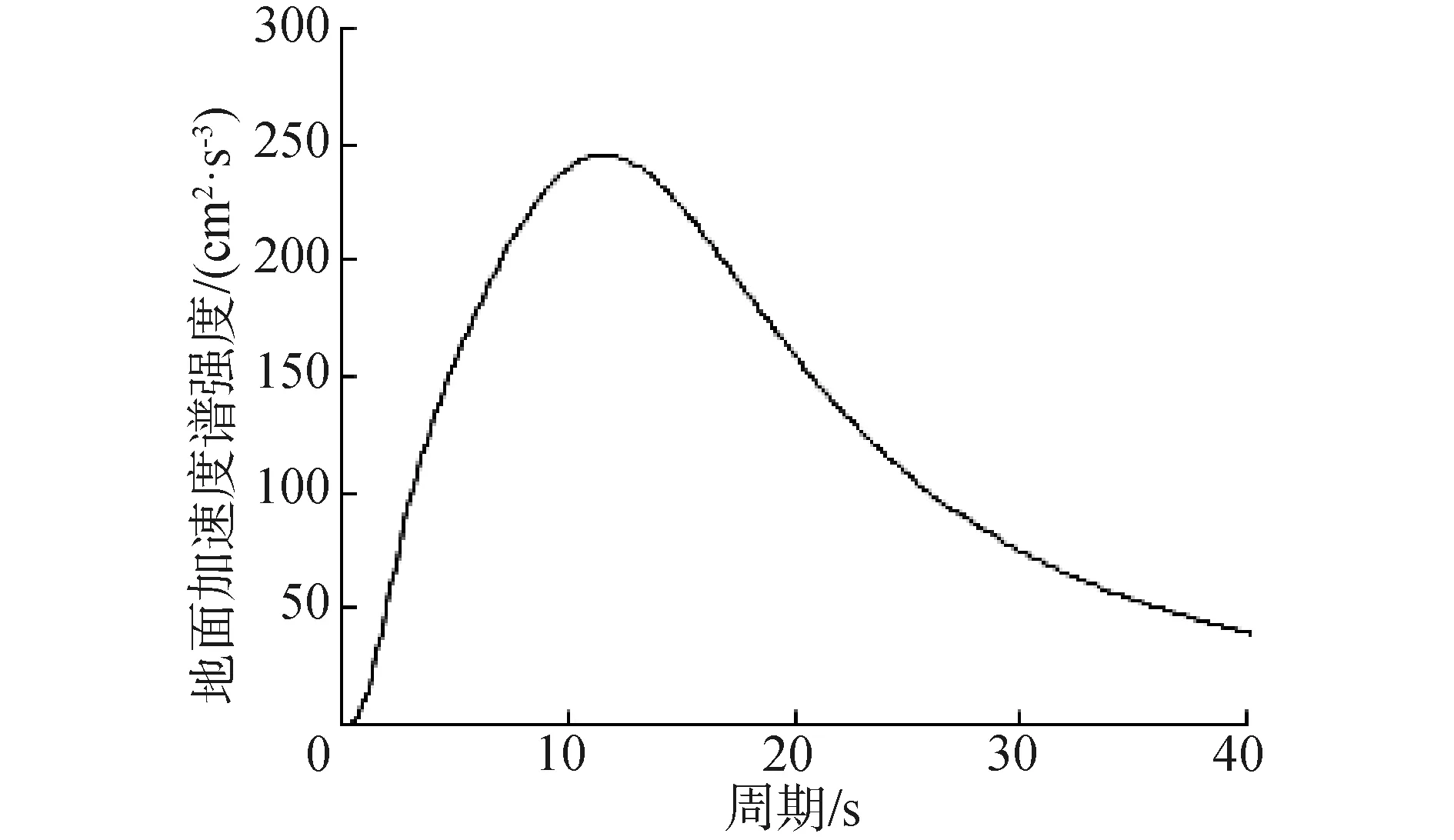
图5 地面加速度功率谱密度函数曲线Fig.5 PSD function curve of the ground acceleration
用SAP2000建立2个结构模型,一个不采取任何减震措施,另一个分别在11、13、15、21、23层设置每层4套X向阻尼器,8层设置2套X向阻尼器,8、10、12、14、16、18、22、24层设置每层4套Y向阻尼器,3层设置2套Y向阻尼器,阻尼器的安装采用套索的形式,阻尼系数CN=1 400 kN/(m·s-1)0.3,速度指数α为0.3,由于频域内的分析不能考虑速度非线性,因此需要根据阻尼耗能相等的原则计算阻尼器的等效线性阻尼系数[16]。
线性阻尼器和非线性阻尼器带给结构的附加阻尼比分别为:
(12)
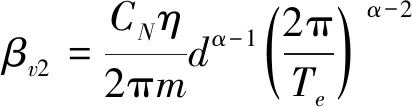
(13)
式中:Te结构基本周期,本例中Te=2.03 s;m为结构质量;d为阻尼器最大变形,本文取结构层间位移角达到 《建筑抗震设计规范》[7]规定上限时的阻尼器变形,d=0.00 735 m;η为计算的中间参数,由下式计算得到:
(14)
令βv1=βv2,则:
(15)
则等效线性阻尼系数为:
(16)
将各个参数值代入式(19),计算得到Ceq=23 144.2 kN/(m·s-1),在SAP2000中将该值定义为阻尼器的线性阻尼系数。
3.2 计算结果分析
对该结构进行功率谱密度分析,选择层间位移角最大的层(18层),分别输出2对比分析结构在该层的层间位移谱强度与频率的关系曲线,如图6所示。
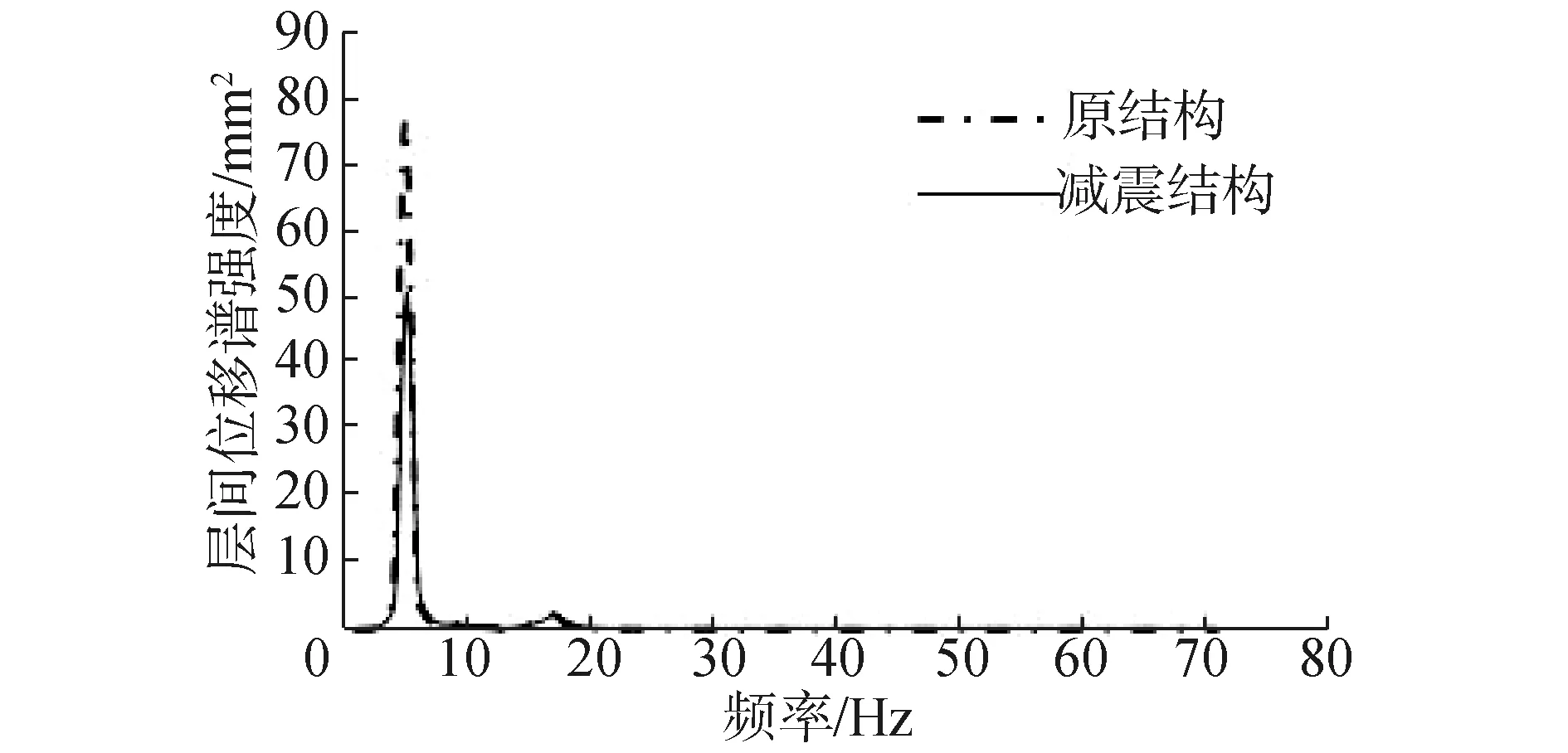
图6 最大层间位移谱强度与频率关系曲线Fig.6 The relation curve of maximum interlayer displacement’s spectrum intensity and the frequency
用1.2节的公式计算第18层层间位移角不超过3.75 mm(根据《建筑抗震设计规范》[7]规定的框剪结构小震下弹性层间位移角限值计算得到)的可靠度,计算结果及中间参数如表4所示。
由表4可以看出,附加液体粘滞阻尼器减震结构层间位移不超过3.75 mm的概率,即结构地震可靠度,由原结构的42.78%提高到48.81%。

表4 可靠度计算中间参数及结果Table 4 Intermediate parameters and results of reliability calculation
阻尼器变形超过极限变形作为结构失效的判断标准,重新计算结构地震可靠度。选取变形最大的一套阻尼器,输出其轴向变形谱强度与频率关系曲线,如图7所示。
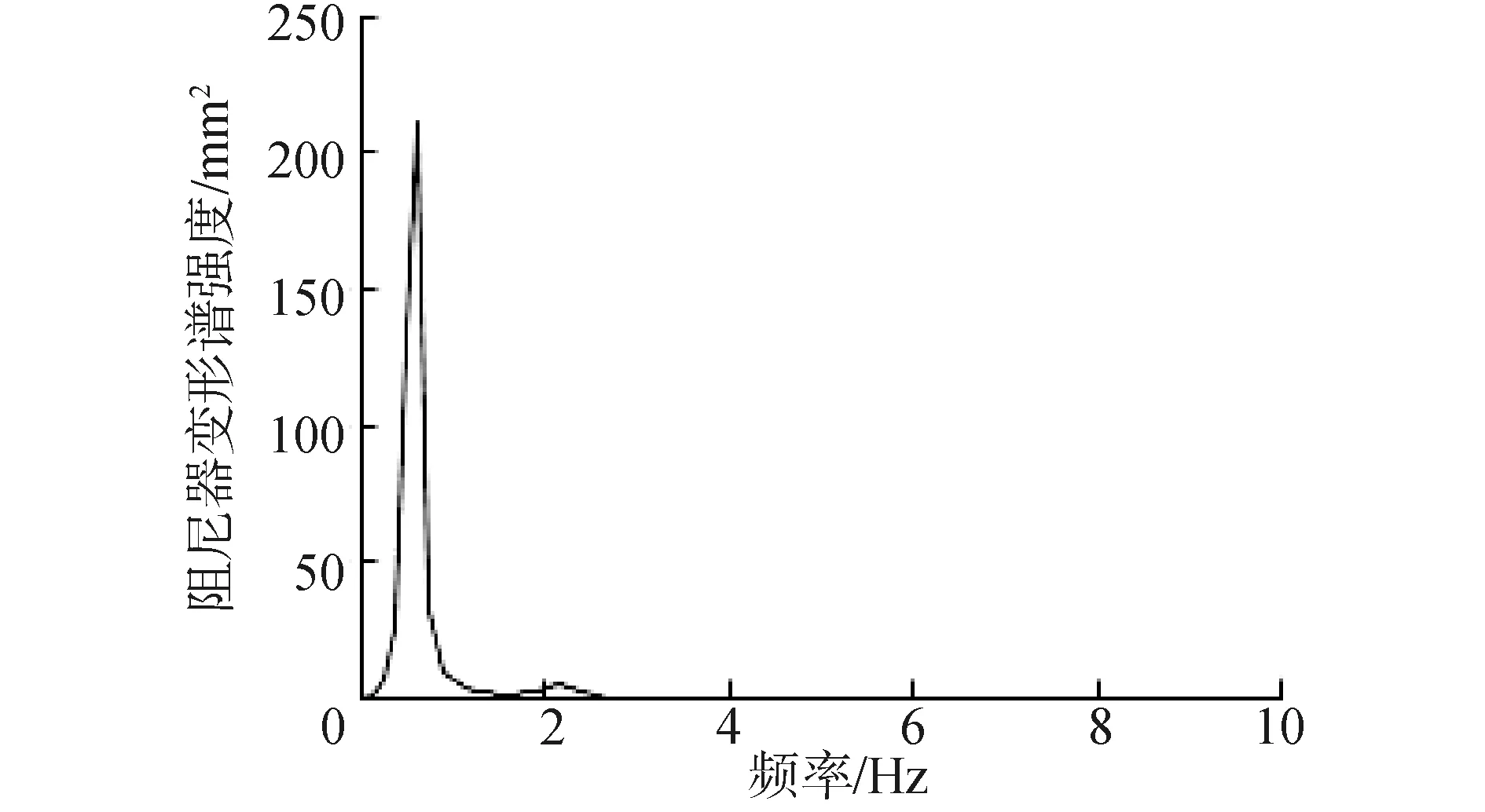
图7 阻尼器最大变形谱强度与频率关系曲线Fig.7 The relation curve of the damper maximum deformation’s spectrum intensity and the frequency
采用式(6)~(9)进行计算,其中λ1的值为251.745,计算阻尼器变形不超过75 mm(由阻尼器生产厂家给出)的概率为100%。
将表4中P1和表5中P2对比,取小值,得到结构最终的地震可靠度为48.81%,可以看出,以结构层间位移角超限作为失效标准起控制作用。
4 结论
1)对于附加液体粘滞阻尼器结构减震效果的计算,采用基于功率谱密度分析的方法与时程分析方法的计算结果更为相似。基于功率谱密度分析方法的计算量较时程分析法小,同时该方法相较于振型分解反应谱法可以更真实的反映出阻尼器对结构的影响,因此该方法更适合于附加液体粘滞阻尼器结构的地震反应分析。
2)基于功率谱密度分析的地震反应分析方法可计算得到结构地震反应的谱强度。频率曲线可直接应用于结构地震可靠度的计算,因此该方法也可应用于基于性能的结构设计和工程地震风险保险领域。
3)基于功率谱密度分析的结构反应分析方法可扩展至统计规律更加明显的结构风响应的计算。

