基于机器学习的非接触式水位计校准算法研究

谢 敏 ，刘秋明 ，肖 贺 ，刘述民

（1. 江西省防汛（水利）信息中心，江西 南昌 330009；2. 江西理工大学软件工程学院，江西 南昌 330031）

0 引言

水位/水深是刻画水流、水体变化的水情要素和重要参数，是水文监测中最为常规的监测要素，也是防洪、抗旱、水资源综合利用、水情信息监测、水文数据预报等工作的基础数据[1]12。近年来，国家在防汛抗旱方面针对中小河流的水位信息感知要求在逐步提高，同时进行水位监测的传感器也从早期功能单一、简单化的仪器逐步被数字控制智能设备替换。常见的水位监测仪器有多种形式，如浮子式、雷达式、超声波式、压力式水位计，以及电子水尺等[2]157。为有效进行防汛减灾和水资源管理，国家对于水位计的数据准确度和精度都有严格的要求[3]。

但是，数字型水位传感器经过长时间使用会产生一定的零点及量程漂移（通常是时漂和温漂），同时生态环境和天气因素也会对传感器产生影响，如果更换传感器会带来许多不便和较大成本。目前国内水利部门普遍采用十米水位试验台[4]对浮子式和压力式水位计（主要包括给排水、水位测井和标准量测系统等部分）进行校准，利用水位测井中的水位升降模拟实际场景，同时高精度水位量测系统提供标准水位数据以便于校准。但在对超声波、雷达式等非接触式水位计进行校准时，十米水位试验台方式存在一定的局限性。十米水位试验台测量内径为 1.2 m，有效测量深度为10m，适用于波束角a≈6° 范围内的非接触式水位计校准。但是，目前雷达式和超声波式水位计采用10m 作为有效测量范围进行计算，且波束角范围约为 12°[1]48，所需要的最小测井内径大小约为D=10×tan 6°×2 ≈ 2.1 m，因此，十米水位试验台可能无法满足校准需求。为保障非接触式水位计监测结果的准确性，并以低成本校准测量数据，提出一种基于机器学习的校准算法，该算法利用误差辗转递送，构建 Boosting 模型，逐步迭代，减少观测误差。

1 测量设备误差分析

非接触式水位计采用波的反射原理，综合反射延时及波速得到水位计探头和水面的相对距离，以测量环境中的水位数据为基础值，依据设定公式推导出被测量水位信息[5]。其中，距离计算公式为

式中：Z为水位计探头至水面距离；v为声波、电磁波或光波的传输速度；t为水位计的探头发送波与接收波的时延[6]。

从超声波水位计超声波的空间传输性质看，超声波发送时受气温、相对湿度和大气压力等外界环境因素影响较大。相关研究实验表明，气温对于超声波传输的影响最大，由此产生的超声波传输速度的波动范围约为 7%。因此，现有的超声波水位计在工作时，必须考虑空间温度的影响，通过多次试验得到温度和误差的拟合结果，并修正水位测量数据的结果，但对超声波水位计内部进行测温得到的温度不能代表超声波发射路径上的环境温度。以10m量程举例，若超声波水位计温度测量产生的误差为1°，可能导致2cm 水位测量结果误差[7]。另外，超声波水位计安装不规范也会使测量数据不准确，主要是由于设备安装水平度不够平整带来的超声波发射角度的变化，因此安装超声波水位计时，需要尽量保证发射波束和被测量表面成垂直状态。但是，现实环境中，由于风力的影响，设备支架会发生振动和摇动，振动影响比较容易处理，而摇动可导致水位计探头出现θ度倾角，将会引起测量结果误差。若设备倾斜时的测量水位高度结果为Z1，而水位高度实际距离为Z0，则水位高度测量结果误差 ΔZ可以表示为

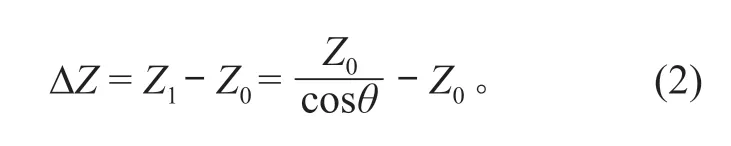
以量程为10m 的水位计为例，如果倾角为 5°，根据式 (2) 计算出的最大测量误差达到 0.038 m，且随着测量范围的增大，所产生的测量误差也会越大[8]。

2 校准算法流程分析

张骏等[9]提出一种集成 Boosting 学习算法，Boosting 算法基于迭代思想，本质是基于同一个测试集采用不同的分类效果较弱的分类器，再集合这些弱分类器构成一个分类效果相对较强的分类器。杨浩等[10]提出基于 Boosting 算法的 Adaboost 的单层决策树模型，能够基于大量弱分类器构建强分类器。针对非接触式水位计存在测量误差的问题，利用机器学习方法的水位计实时校准算法，即通过采集前期历史水位高度误差数据样本及其周边环境数据（包括风速、温湿度、PM10 等数据），构建神经网络模型，将采集数据输入该模型进行训练，融合水位计的环境参数，利用训练后的模型预测当前采集到的水位高度误差值，并利用误差辗转递送的水位计数据进行实时校准，可提高水位计的精度和准确度。基于机器学习方法的水位计实时校准算法，非常适用于无法直接构建强分类的场景，可为构建强分类器提供一种普适和有效的新思路。

水位高度校准算法流程如下：1）首先对模型初始化，然后将最新时间段的标准的和水位计采集的数据导入模型中，利用改进谢别德插值算法对采集的标准数据进行处理[11]，得到与水位计设备采样频率及分辨力相等的标准插值数据；2）将经过插值后的标准的及水位计设备的数据，置入构建好的 Boosting 模型；3）基于上一次模型得出的误差数据，对本次 Boosting 模型输出的数据结果进行校准，保留校准值；4）等待标准数据的更新，利用该标准数据更新校准的误差值，并将更新误差辗转递送给下一次模型。

Boosting 模型使用基于单层决策树的 AdaBoost模型，训练数据集输出校准值，其算法流程如图 1所示。

图1 Boosting 模型算法流程图

利用误差辗转递送的水位测量数据实时校准算法步骤如下：

1）模型建立。利用多次实验得到的全部信息确定模型参数误差，并将初始值定为 0。模型每次使用的训练数据集大小为45000条，为使总体误差得到有效控制，多次校准后的误差小值足够多，从而提高模型可接受信赖度，误差影响率控制为 0.1，但由于模型数据集过大会产生数据过拟合，因此确定每次校准的数据为15个。

2）数据实时校准。实时采集最新时间段标准的和设备测量的数据，并保存至实时数据库，利用改进谢别德插值算法对采集的标准数据采样频率进行处理，根据最小二乘法求解每个节点的节函数Qk(x，y)，推导出改进谢别德函数D[f](x，y)，最后，利用牛顿插值法求得改进谢别德函数值数据，公式如下：

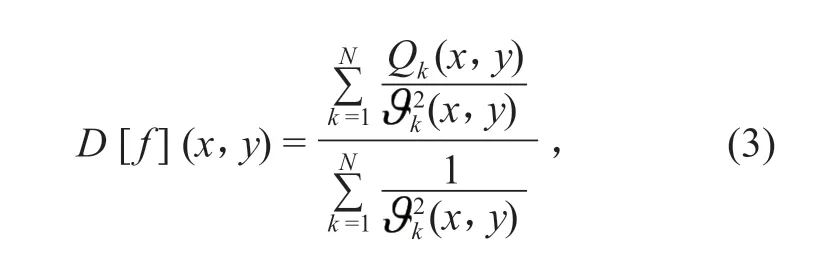
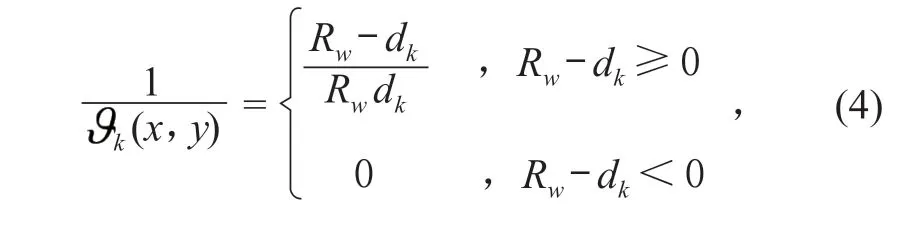
式中：Rw表示插值区域内节函数可以影响的半径；dk表示待插值点与其领域内第k个点之间的欧几里得距离。

3）模型训练。将插值后的标准的及设备测量的数据置入构建好的基于单层决策树的 Adaboost 模型中，首先训练数据中的每一个样本，并给每个样本赋予一定权重，权重系数构成向量W，然后通过迭代计算得到数据集的错误率，其中本次样本的权重根据上一次分类的对错情况进行重新调整，将本次的错误率与之前的错误信息不断进行比较和更新，最后得到错误率最小的单层决策树。对于决策树算法，通过大量数据集样本的分析描述一个水位数据分类规则，根据决策树模型得到新数据分类结果。根据算法流程，可以得到决策树算法的时间复杂度为O（NlogN×d）（N表示数据集中的样本数，d表示数据的维数）。使用辗转递送的方法，采集最新一次的标准数据以更新校准误差，将误差递送给下一次模型。

4）误差更新。利用格拉布斯准则去除m个数据的误差，对结果取均值检测每一个异常值，并迭代更新误差值直到没有异常值。如果某个测量值的残余误差Vi的绝对值满足 |Vi|＞Gg（Gg表示第g次迭代的误差平均值的绝对值），则可以推断出该误差结果较大，需要剔除，即若某个测量值xi对应的残余误差Vi满足下列条件时，该数据会被去除掉：

式中：n表示测试的次数；x表示n次采集数据的平均值；a为显著性水平，通常取 0.01 或 0.05；σ(x)为对应测量数据组发生“弃真”错误的概率函数。

3 校准算法结果分析

根据校准算法理念，本研究采集赣江某监测点1个月的水位数据，采用 SEBAPuls20 雷达水位计作为自建点采集设备，测量范围为 0～35 m，测量精度为 ±2cm，输出 4～20 mA 电流信号，水位数据采样为1次/h。校准算法仿真结果如图2所示，其中蓝色曲线为自建点采集设备实际采样的水位数据值，黑色曲线为标准设备采样值，红色曲线为误差辗转递送的强学习算法的校准值。从图中可以看出，自建监测点和标准设备采集数据存在一定的误差，利用校准算法能够减小自建点和标准设备采集的误差，且能够很好地拟合标准设备的采样值，虽然校准之后的数据与标准数据也有一定偏差，但校准数据满足标准规定的10cm 精度指标要求[2]157，从而可减少人工校准设备的工作量。

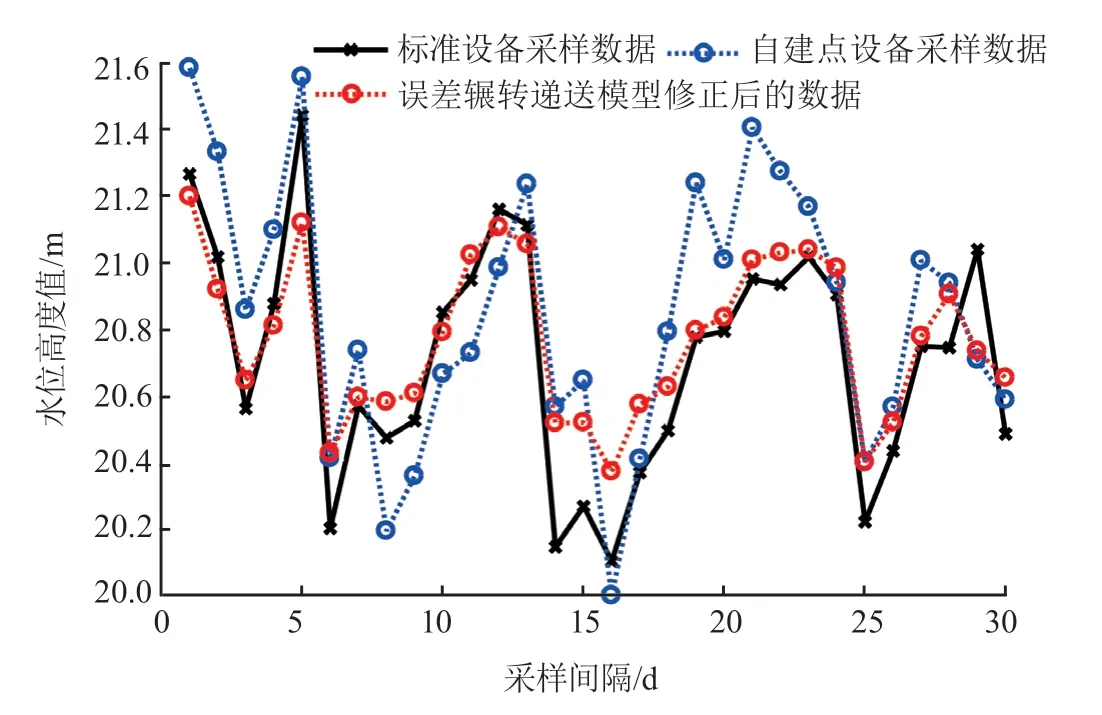
图2 校准算法仿真结果

4 结语

本研究围绕现有非接触式水位计测量技术和误差产生的原因，利用机器学习的思路和方法解决了非接触式水位计误差校准的问题。通过搭建神经网络模型训练历史数据集，发现非接触式水位计测量值与环境因素存在一定的关联。水位测量误差校准算法结果表明，该算法能够融合环境因素的影响且很好地拟合水位测量误差，并逐步逼近标准设备采集的数据值。与传统校准方法相比，本研究提出的校准方案将前端设备校准移到后端软件层面，为非接触式水位计校准提供新思路，大大提高了校准工作效率。