基于信息熵的在线考试组卷策略研究
董晓睿,商 凯,崔 健,邸文华
(1.中国石油大学胜利学院,山东东营 257000;2.山东天元信息技术有限公司,山东济南 250100)
0 引言
考试是检测学生学习水平和教师教学效果的重要手段。2020年以来,由于新型冠状病毒的影响,在线教育迎来首次全国大规模推广应用落地,绝大部分高校将期末考试形式由集中纸笔考试调整为居家在线考试,智能公平高效合理的在线考试系统成了研究热点[1]。无论是传统纸笔考试,还是当前在线考试,试卷通常都是由命题人组卷,组卷过程[2]极易受到命题人的主观因素影响,导致最终生成的试卷难度无法把控,无法达到对学生学习水平理想的检测效果。如何充分利用信息技术,建立公平合理的组卷策略,是当前亟待解决的问题之一[3]。
针对这一问题,本文提出了一种基于信息熵的在线考试组卷方法,该方法可以基于历史试卷作答数据,为每道题赋予合理的试题难度评分,避免了随机抽题过程中忽视试题难度或者人工制定试题难度时的不合理情况。同时,本课题基于这种组卷方法,以“数据结构”课程为研究对象,建立了在线考试系统,让任课老师有更多的精力去思考题库建设工作,命题老师只需指定考查知识点、试卷整体难度等约束,组卷过程由计算机自动完成,极大地节约了人力和财力,提升了考试过程的工作效率。
1 题库设计
本方法以计算机类基础课“数据结构”为研究对象,设计题型包括单项选择题、填空题和编程题。其中,单选题由题干、4 个备选项和1 个正确答案组成;填空题由题干和正确答案组成,若题干中包含多个待填项,则填写正确答案时使用中文分号对多个答案进行间隔;编程题包括题干、样例输入、样例输出和编译语言组成。单选题和填空题采用比对作答内容和正确答案的方式进行阅卷,编程题的阅卷过程集成online judge 平台进行代码检测,每道编程题均有10个测试用例,按照正确的测试用例个数给予评分。系统根据考察章节、知识点和试卷整体难度(均值与方差)等约束,从选择题、填空题和编程题题库中抽取试题,组成试卷。题库所涉及的具体数据库设计细节如图1 所示,其中,粗体为必填字段,非粗体为可空字段。
2 试题难度系数计算
本课题运用信息熵理论,基于往届学生作答的历史试卷数据,计算每道题目的试题难度系数。信息熵理论[4]由Shannon 在1948年提出,现常被用来作为一个系统的信息含量的量化指标,用来作为系统方程优化的目标或者参数选择的判据。信息熵可视为是描述变量不确定性的指标,采用离散的概率分布进行表示,分布越广表示系统越不稳定,越集中表示系统越稳定[5]。传统方法一般不考虑题目的难度或者由命题人主动评价题目难度,这是不合理的,本课题通过分析数据本身的离散性,来对试题难度进行客观赋权,降低个人主观因素影响,保证组卷的难度均衡。
定义某试题的历史作答记录X,X包含n条记录,有m项指标。试题类型为选择题时,m=4;试题类型为填空题时,m为填空个数(即分隔符个数+1);试题类型为编程题时,m=10。不同试题类型的计算过程类似,后续部分以选择题为例介绍。定义xij为第i条记录的第j项指标的数值,其中i=1,…,n,j=1,…,m,其值为:

对数据进行归一化处理,为了保证归一化的计算过程中分母不为零,对X进行处理,处理过程为:

定义归一化后的数据为x′ij,其值为:

则第j项指标的熵值ej为:
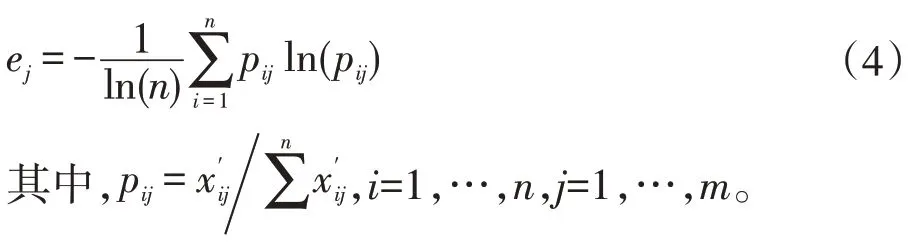
定义各项指标的熵权值为wj,其值为:

定义该题的正确答案的选项索引为correct_index,难度系数为di,熵权值方差为D(w),则难度系数的计算公式为:

di越大,表示该题正确率越低,难度越大,越可能是知识盲点。当di>0.5时,D(w)越大,代表学生对该知识点有错误的理解;D(w)越小,代表学生对该知识点了解较少,存在教学盲点。
3 组卷策略
教师在组卷时,需要根据考试大纲选取章节、知识点、题型、题数、分值、试卷难度、必选题型等约束,使得生成的试卷质量有所保证。组卷策略能够在各种约束条件规定下实现组卷,既要检验学生对知识点的掌握情况,又要有所区分度,对试卷整体难度要有一定的把握。整个组卷策略包括预处理过程和组卷过程,预处理过程需要遍历计算更新试题库中各试题的试题难度,组卷过程在保证约束条件的前提下完成试卷的生成,组卷过程可以通过运行多次来实现随机组卷。预处理过程的输入为试题库和历史作答记录,输出为题库中的试题难度系数和熵权方差,算法主要是遍历题库过程中对历史作答记录进行分析,如公式(1)、(2)建立该试题历史作答记录矩阵X,如公式(3)完成归一化处理,如公式(4)计算样本比重和指标熵值,如公式(5)计算指标熵权值,如公式(6)计算难度系数和熵权方差,最后更新试题的试题难度信息和熵权方差信息。

图1 题库涉及的数据库设计
为了提高系统响应效率,组卷过程不直接使用浮点数的试题难度系数进行计算,而是将难度值划分为五档,分别定义区间[0,0.2)、[0.2,0.4)、[0.4,0.6)、[0.6,0.8)、[0.8,1.0]来表示简单、较简单、中等、较困难、困难,用离散整数(1,2,3,4,5)来取代浮点数来表示试题难度,以减轻随机抽题过程的服务器运算负载。
组卷过程[6]既要满足教师设置的对试卷各要素的约束,又要保证抽题过程的随机性,以达到随机组卷的要求。主要思路为根据题型、题数和难度的约束,逐次在未被抽取到的题目范围内随机抽题,直到该章节、知识点、题型和题数约束的题目全部抽取完毕,随机抽题过程需要保证,越接近难度约束的试题越容易被抽到,但难度偏离较大的题目也有被抽到的概率。为了进一步预防都是难度偏离大的题目被抽到,在每次抽取完毕后,会更新局部难度约束。组卷过程的算法如表1所示。

表1 组卷过程算法
4 结语
本课题基于信息熵理论提出了一种在线考试组卷方法,一定程度上降低了命题人组卷过程的主观因素干扰,同时也为随机组卷方式提供了难度平衡策略。组卷策略使得命题老师只需指定考查知识点、试卷整体难度等约束,组卷过程由计算机自动完成,试题难度系数由计算机根据历史答卷数据进行自动确定,极大地节约了人力和财力,提升了考试过程的工作效率和公平性。本课题案例采用“数据结构”课程为研究对象,本算法对相关系统的设计和实现具有一定的参考意义。

