一种基于RS编码的NHZ跳频序列构造方法*
张笑宇,冯永新,钱 博
(沈阳理工大学辽宁省信息网络与信息对抗重点实验室,沈阳 110159)
0 引言
跳频技术具有良好的抗多径性、抗干扰性和抗衰落性,可极大提高通信系统的抗截获和抗干扰能力[1]。良好的跳频序列集可有效提高跳频通信系统的性能。由于跳频序列集的碰撞概率与最大汉明相关值成正相关,为了减小跳频信号间的碰撞概率,基于无碰撞区(NHZ)跳频序列的构造方法被广泛研究。
常用的生成NHZ跳频序列的伪随机序列主要有m序列[2-3]、M序列[4-5]、GOLD序列[6-7]和RS码[8]等。相对于其他伪随机序列,RS码生成的跳频序列可有效增加跳频图案用户数量,同时改善通信系统抗干扰性能[9]。但直接将RS码应用于NHZ序列的构造,序列的汉明相关值高,跳频序列集的碰撞概率高,因此将RS码应用于NHZ序列的构造存在一定的局限性。
相对于传统RS构造的NHZ序列,宽间隔跳频序列有利于对抗跳频信号中的单频窄带、跟踪和宽带阻塞式干扰,也有利于抗多径衰落;同时宽间隔有利于增强序列的汉明互相关性,降低序列的碰撞概率,因此文中提出了一种宽间隔跳频序列构造方法,分析其汉明相关性,建立矩阵旋转的无碰撞区跳频序列构造算法,通过误码率分析抗干扰性能。
1 RS编码
RS码是一种最佳的近似正交码,具有很好的互相关性;与同样长度的其他伪随机序列相比,RS码可供选择的码数更多;RS码是最小距离最大码(MDC),该性质有利于构造性能较好的宽间隔跳频序列,同时RS码的硬件实现也较简单[10]。
对于长度为L的RS(L,2) 序列,其中码多项式的表达式如式(1)所示。
(1)
其中,码长L=q-1,信息位b取值是2,此时RS(L,2)的性能最优,可以构造出最佳的RS跳频图案[11]。纠正最大的错误数是t,监督元数2t=L-b,RS码在GF(q)上的一个符号序列,每个符号用m个比特表示,q=pm=2m-1,最小码间距离d=2t+1。
设b位信息为ν0、ν1,信息向量是V=(ν0,ν1),νi∈GF(q);α是属于q的本原元,生成矩阵表示为:
(2)
则RS(L,2)码的码字向量可表示为:
Sν=VGb×(q-1)
(3)
由于典型的数据链系统Link-16的跳频频点数目为51[12],文中选取L=63,RS编码选取RS(63,2)。信息向量中ν1=000001,ν0取0~63时,可生成64个非重复跳频序列。当ν0=0时,根据伽罗华域GF(26)中元素的生成多项式f(x)=x6+x+1,RS(63,2) 序列编码电路如图1所示。

图1 RS(63,2) 编码原理图
2 宽间隔跳频序列构造方法
为实现最大的跳频处理增益,跳频序列的设计需满足完备频率集中的所有频率,且跳频序列应具有良好的汉明相关性,同时为实现保密和抗干扰通信,跳频序列集中的序列数目尽可能多,且各频点在一个序列周期中出现是等概率的。
虽然RS码的周期越长,构造的跳频图案性能越好,但同时也会增加实现的难度,降低工程的应用价值。经过RS(63,2)编码后的序列为:{1 2 4 8 16 32 3 6 12 24 48 35 5 10 20 40 19 38 15 30 60 59 53 41 17 34 7 14 28 56 51 37 9 18 36 11 22 44 27 54 47 29 58 55 45 25 50 39 13 26 52 43 21 42 23 46 31 62 63 61 57 49 33}。此时的序列由于没有经过交织处理,其跳频间隔和汉明相关值较低,碰撞概率较高。
为保证RS生成的跳频序列具备不可逆推性和较强的抗干扰性,构造的跳频序列应具有较宽的间隔。对于已经确定跳速的系统来说,将跳频序列设计成宽间隔,有利于对抗单频窄带干扰、跟踪干扰和宽带阻塞式干扰,也有利于抗多径衰落。因此,通过对原RS(63,2)序列进行抽样、交织处理,进一步增大跳频序列间的平均间隔,增强序列的汉明互相关性,降低序列的碰撞概率。
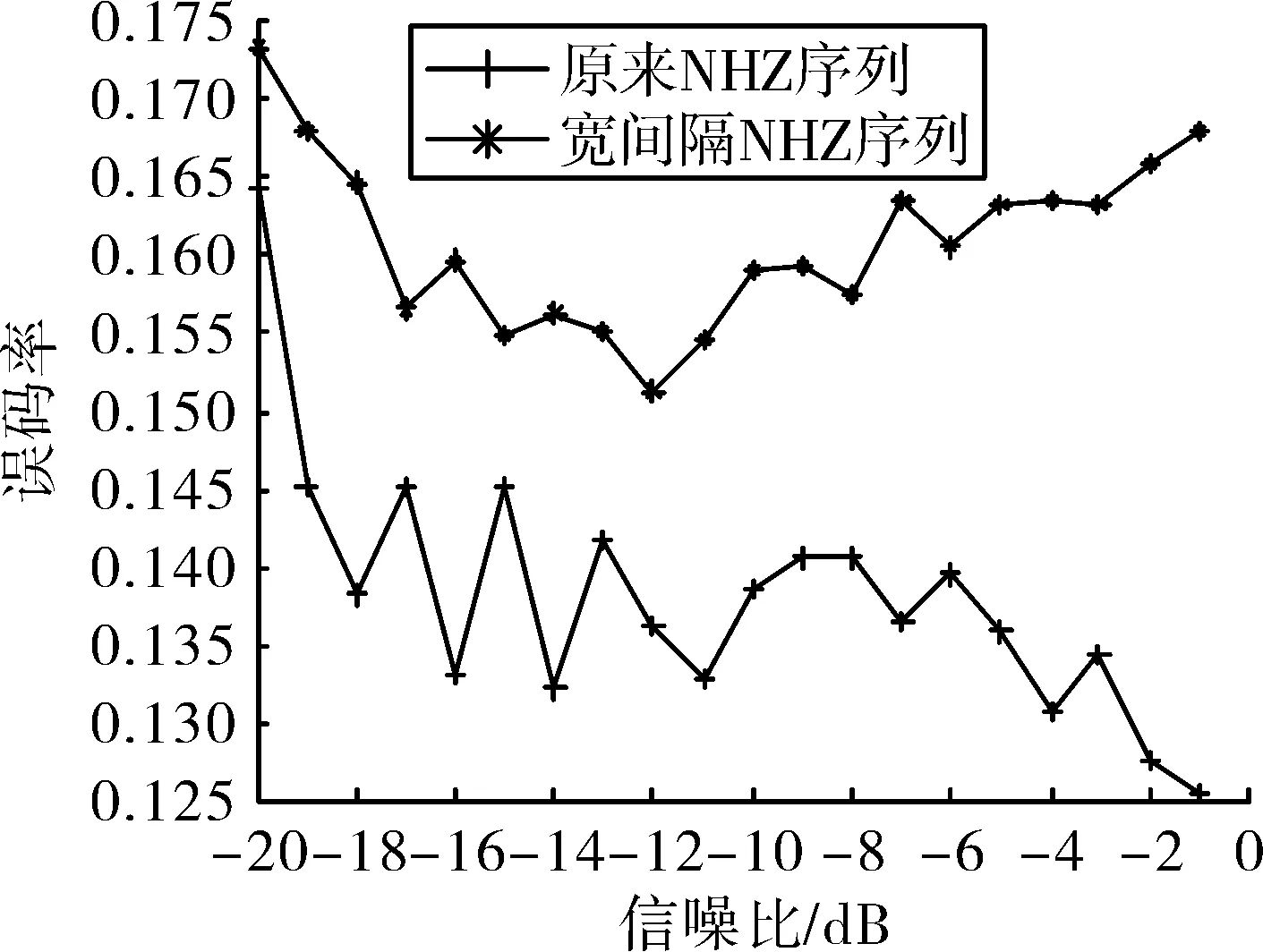
其中,在RS(63,2)序列的抽样中每隔N(N 经计算,当N=3时,优化后序列的跳频平均间隔可从15.516 1增大到23.580 6。 (4) 其中: (5) ∀Sx∈S,0<|τ|≤T}} (6) ∀Sx,Sy∈S,0<|τ|≤T,Sx≠Sy}} ZNH=min{ZAN,ZCN} NHZ跳频序列集S可定义为S(q,L,N,ZNH;λ),其中q是频点个数,L是序列长度,N是序列数目,ZNH是无碰撞区长度,λ是S的最大汉明相关值。 基于矩阵转换[17]的NHZ序列构造方法的主要思想如下:将S从左到右均匀分为X个小块,每个小块恰好包含S的(ZNH+ 1)个列,分别记为Pi。由文献[18]中S的构造条件可知,Pi可以通过列循环移位得到。因此,在任何位置的N×(ZNH+ 1)窗口上循环平移,跳频序列不会发生碰撞。为进一步增大跳频序列的跳频间隔,降低跳频序列的碰撞概率,依据上述思想,文中设计的基于RS编码的NHZ序列构造方法如下: 1)将序列S变换成m1×m2的矩阵S1,设m1=N,m2=q/N,S1=[S0,S1,S2,S3],把S1随机分成m1×k1,m1×k2的子序列,C1=[C1,0,C1,1,C1,2]=[S0,S2,S3],C2=[C2,0]=[S1],其中k1=3,k2=m2-k1,变化C1,即把列C1,1循环移位t1位,0 2)令生成矩阵C3=[C3,0,C3,1,C3,2]=C1,变化C3,即把列C3,0循环移位t2位,C3,1循环移位t3位,C3,2循环移位t4位,其中设t2=1,t3=3,t4=2,0 例 令S={1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16},N= 4,k1= 3,k2= 1,则基于矩阵旋转后构造的T(16,7,4,2)如下:T={1 11 4 6 13 15 12;5 15 8 10 1 3 16;9 3 12 14 5 7 4;13 7 16 2 9 11 8},构造跳频序列的汉明自相关结果分别如图2~图5所示。 图2 序列T9的汉明自相关性图 图3 序列 T1、T2的汉明互相关性图 图4 序列T0、T3的汉明互相关性图 在相对延时为0≤|τ|≤L-1时,从图3可以看出在τ=0时,跳频序列T0的汉明自相关值达到最大为 7 ,当τ≠0时,汉明相关值处处为零;从图4至图5可以看出,无碰撞区ZNH=2,且仅在|τ|=3和4时,存在汉明互相关值,汉明互相关最大值是 1 ,同时可以验证T0与T1、T0与T2、T1与T3的无碰撞区ZNH均为2,且仅在|τ|=3和4时,存在汉明互相关值,汉明互相关最大值是1。 文中构造的NHZ序列汉明互相关值远小于原来的NHZ序列,因而若在无碰撞区范围内接入跳频网络时,可显著提高跳频系统的抗多址干扰能力。 在MATLAB7.1 软件环境下,通过分析误码率来验证改进后基于RS编码的跳频序列抗多址干扰性能。仿真参数如下:调制方式为CPFSK,其中调制系数为5/9;跳频信号的码速率为 200 kbit/s;中频频率为 30 MHz;采样频率为3 GHz;跳频驻留时间为150 μs;跳时间隔为50 μs;跳周期为 200 μs;跳频速率为5 000 hops/s;跳频频率集为902~927 MHz,具体的频点划分如图6所示。 按照改进后的NHZ序列生成五跳跳频信号,其时域、时频域结果如图7、图8所示。 图8 五跳NHZ序列的跳频时频域 进一步,根据一般跳频系统中的用户数目,在不同信噪比下,对构造的NHZ序列性能进行仿真验证,两种跳频序列的系统误码率如图9~图12所示。 图9 两路用户下系统误码率关系曲线 从图9可以看出,当两路用户的时候,采用宽间隔的NHZ跳频序列和传统的基于RS的跳频序列的系统误码率相当。由图10可知,当用户增大至四路时,采用宽间隔的NHZ跳频序列的系统误码明显优于传统的序列,但两种序列的误码率曲线波动较大。由图11可知,当系统存在八路用户的时候,采用宽间隔的NHZ跳频序列的系统误码优于传统的序列,且两种序列的误码率曲线变化较为平坦。由图12可知,用户增大至十六路的时候,虽然两种序列的系统误码率均有所增大,但采用宽间隔的NHZ跳频序列的系统误码仍优于传统的序列。随着跳频组网用户的逐渐增大,宽间隔的NHZ跳频序列集的系统性能优势越大。 图10 四路用户下系统误码率关系曲线 图11 八路用户下系统误码率关系曲线 图12 十六路用户下系统误码率关系曲线 在信噪比为-10 dB的情况下,两种跳频序列在不同跳频用户系统误码率结果如图13所示,随着用户数目的增加,两种跳频序列的系统的误码率均有所增大,但基于RS编码所构造的NHZ序列的系统误码率明显低于传统NHZ序列的系统误码率,即在无碰撞区范围内接入跳频网络时,改进后的RS编码所构造的NHZ序列可有效提高跳频系统的抗多址干扰能力。 图13 两种跳频序列的误码率关系曲线 在分析RS编码机理的基础上,针对基于RS(63,2)编码产生的跳频序列频率碰撞概率较高的不足,提出了一种宽间隔的跳频序列产生方法,并利用生成的宽间隔RS跳频序列,构造无碰撞区跳频序列。通过仿真结果表明,改进后算法序列的汉明互相关值明显减少,频隙间隔明显增大;且在无碰撞区范围内接入跳频网络时,可显著提高跳频系统的抗多址干扰能力。3 基于RS编码的NHZ序列构造算法

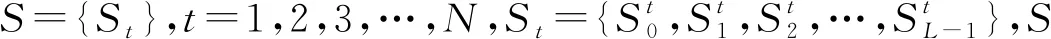

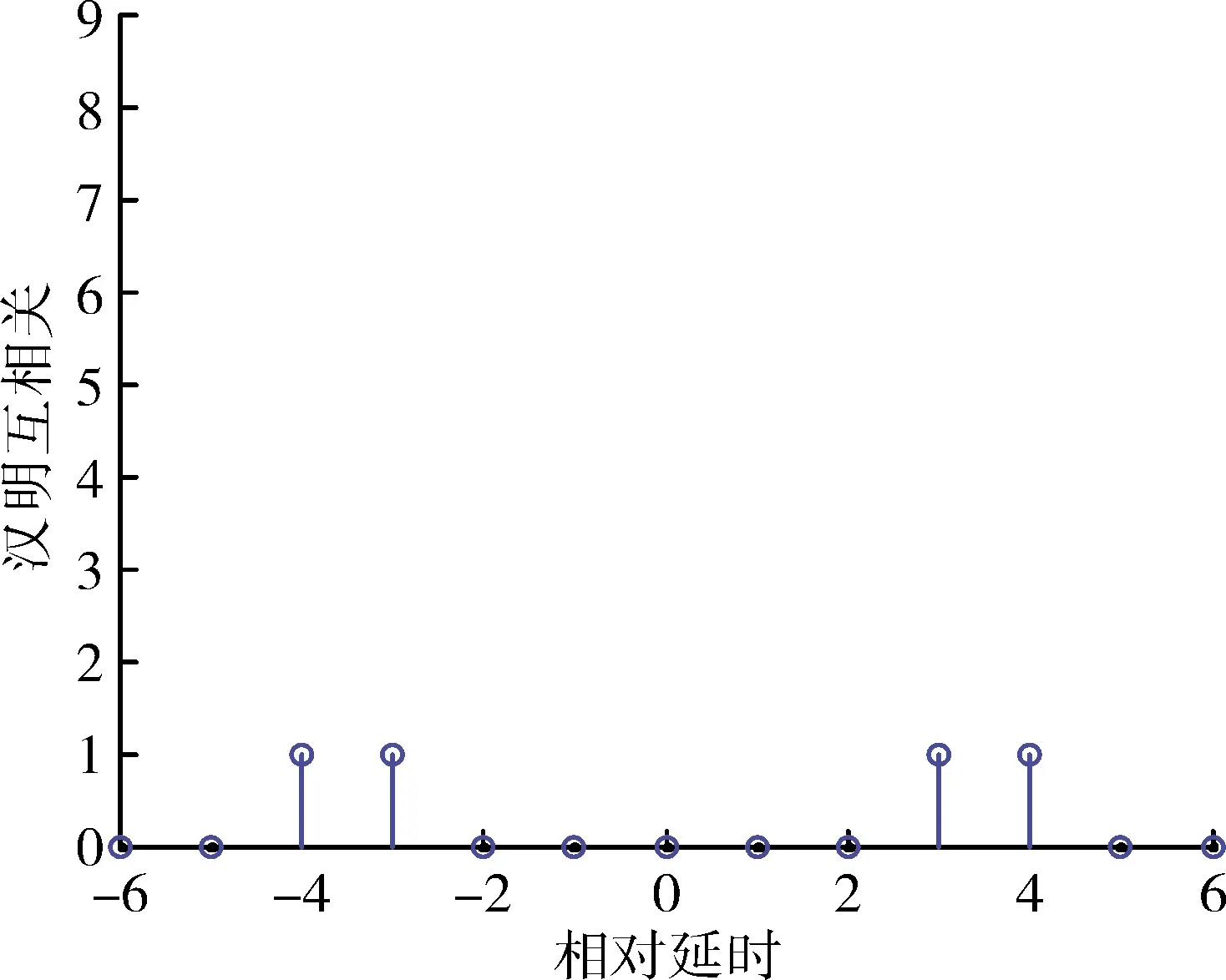
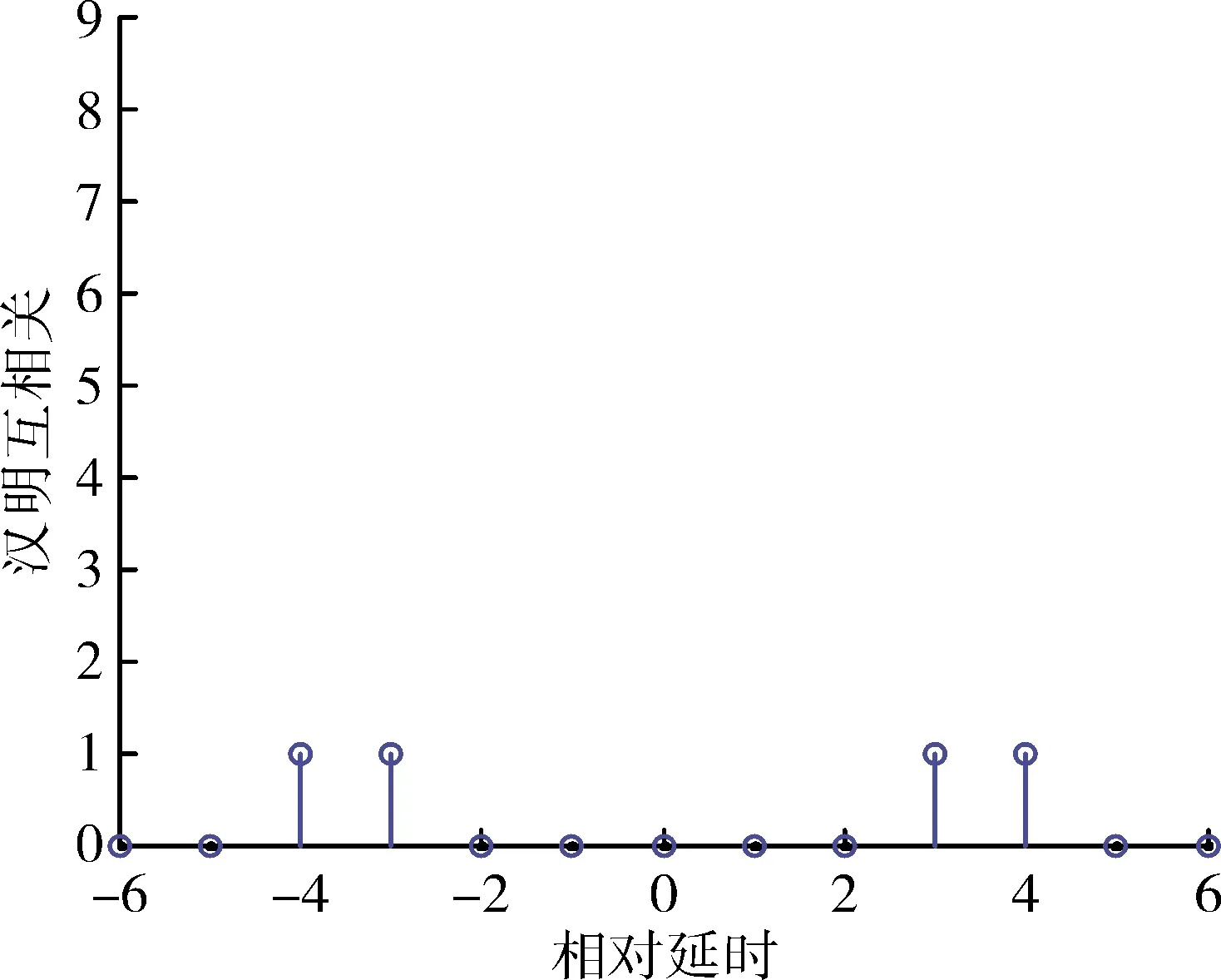
4 仿真与分析

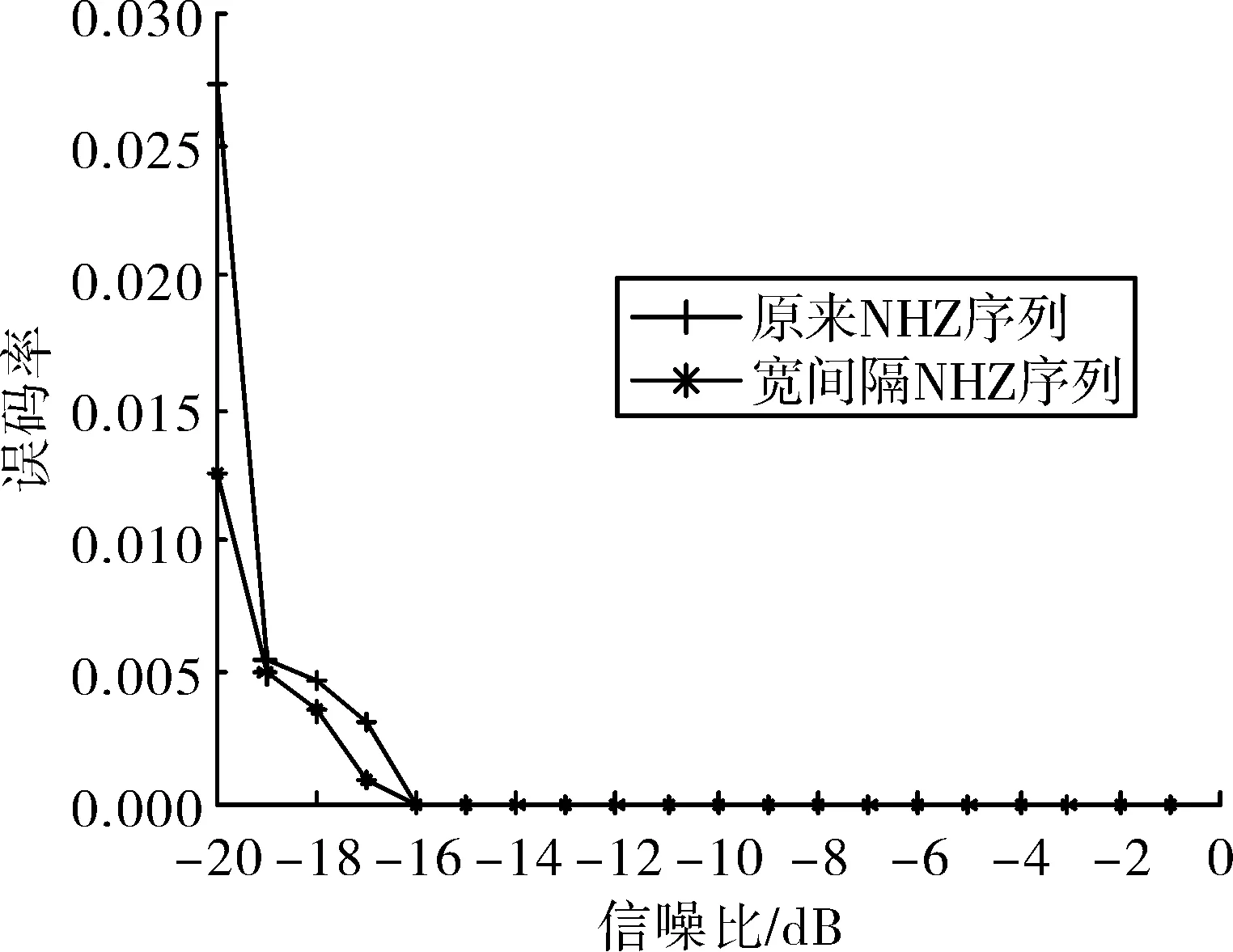



5 结论

