基于Lyapunov动态队列控制技术的施工期能耗权衡设计
何 威,李 伟
(燕山大学 a.建筑工程与力学学院;b.河北省土木工程绿色建造与智能运维重点实验室,河北 秦皇岛 066004)
能源问题长期以来是人类关注的热点[1],能耗控制也是人类持续努力的重要方向[2],建筑业能耗是全球总能耗的重要组成部分,在中国这一比例已经高达40%[3],建筑业能耗分为材料制造能耗、施工能耗和运行能耗[4],其中建筑施工能耗约占建筑物全生命周期总能耗的23%,在低能耗建筑中该比例甚至高达40%~60%[5],施工能耗的研究已经成为业内专家学者工作的着重点,施工能耗量也成为项目竣工验收的重要指标之一,现阶段建筑企业通过计算各类能耗定额[6]进行粗浅的能耗统计,并没有一套贯穿施工期的能耗实时权衡分析方法。施工能耗的控制分析不仅可以提高施工项目的经济效益,还可以降低资源浪费实现社会效益,通过对施工现场的数据挖掘,利用智能算法实现施工能耗分析的可视化,并以此构建施工能耗数据库[7,8],对拟建工程进行能耗预算,因此施工期能耗的精准分析和有效控制[9~11]对推动建筑行业的能耗管理具有重要意义。
针对施工能耗各国专家学者多年来做了大量的研究工作,相关研究成果给予建筑行业丰富的理论基础,主要工作集中在三个方面:(1)施工能耗定额分析研究:在住宅建筑施工初始能耗定量计算[12]中,分析了各阶段能耗的比例和能耗定额计算值,针对碳排放做出了计量分析[13]等工作;(2)节能施工技术:通过对建筑技术的统计分析[14],在施工能耗控制上利用NB-IoT等技术给建筑行业带来了较好的经济效益[15],并且促进施工节能技术的发展;(3)建筑能耗监测:根据多年来对中国建筑能耗现状特征[16]的探析,发现合同能源管理模式下的公共建筑能耗监测存在风险[17],利用BIM(Building Information Modeling)协同优化方案对建筑能耗进行了系统性分析[18]等相关研究,随后有关学者对施工能耗进行了多目标优化[19],得到了适用的调度方案。但是现存工作中忽略了施工期随机事件和施工方式对施工能耗的影响分析,目前随机性的研究很广泛[20~22],在施工和管理中尤为突出,并且随机性事件的影响概率分布很难被统计出来,已有工作都是在理想化约束条件下完成的,因此在考虑施工期随机性事件和施工方法的前提下,对施工能耗进行权衡分析是一项有研究意义的工作。
本文根据前人研究和现存问题,利用处理动态队列控制的Lyapunov drift-plus-penalty技术[23~25]应用于施工期能耗的权衡分析,该技术本身的突出优势在于考虑随机性事件过程中不需要知道其概率分布[26],以此处理施工期随机性事件下的施工能耗权衡问题具有良好的结合性。通过构建施工队列和虚拟队列[27],引入二次Lyapunov函数,进行函数漂移后把目标函数引入惩罚边界[28],实现算法的漂移加惩罚。以实际工程项目为实验背景,分析施工期能耗的动态关系[29],可以实现施工能耗数据可视化、多影响因素权衡分析和精准施工能耗管理的目的。
1 问题表达与建模
1.1 问题描述
在基于Lyapunov动态队列控制技术的施工期能耗权衡模型设计过程中,目的是解决土木工程施工期内的能耗权衡和控制问题,使施工期内工程管理的特性细节化。将研究问题划分为三个阶段进行处理,第一个阶段是建立动态施工队列,首先要根据施工期工序的先后状态将其进行编排,构造施工队列函数Qi(t+1),然后将进度划分为由单位时间槽t(工日)组成的时标轴(T—正常工期;T′—应急工期);第二阶段是利用Lyapunov动态队列控制技术进行算法设计,构建虚拟施工队列,考虑到施工中随机性事件对能耗的影响,使用drift-plus-penalty算法,突出惩罚参数V的控制影响;第三个阶段是将Lyapunov动态队列控制技术应用于实际工程案例,构建时变工期和能耗函数T(t),E(t),调查勘测出各阶段实际能耗数额,以惩罚参数V来控制多余浪费的能耗工序,经过权衡后进行详细分析,文中所用函数的表达含义如表1所示。
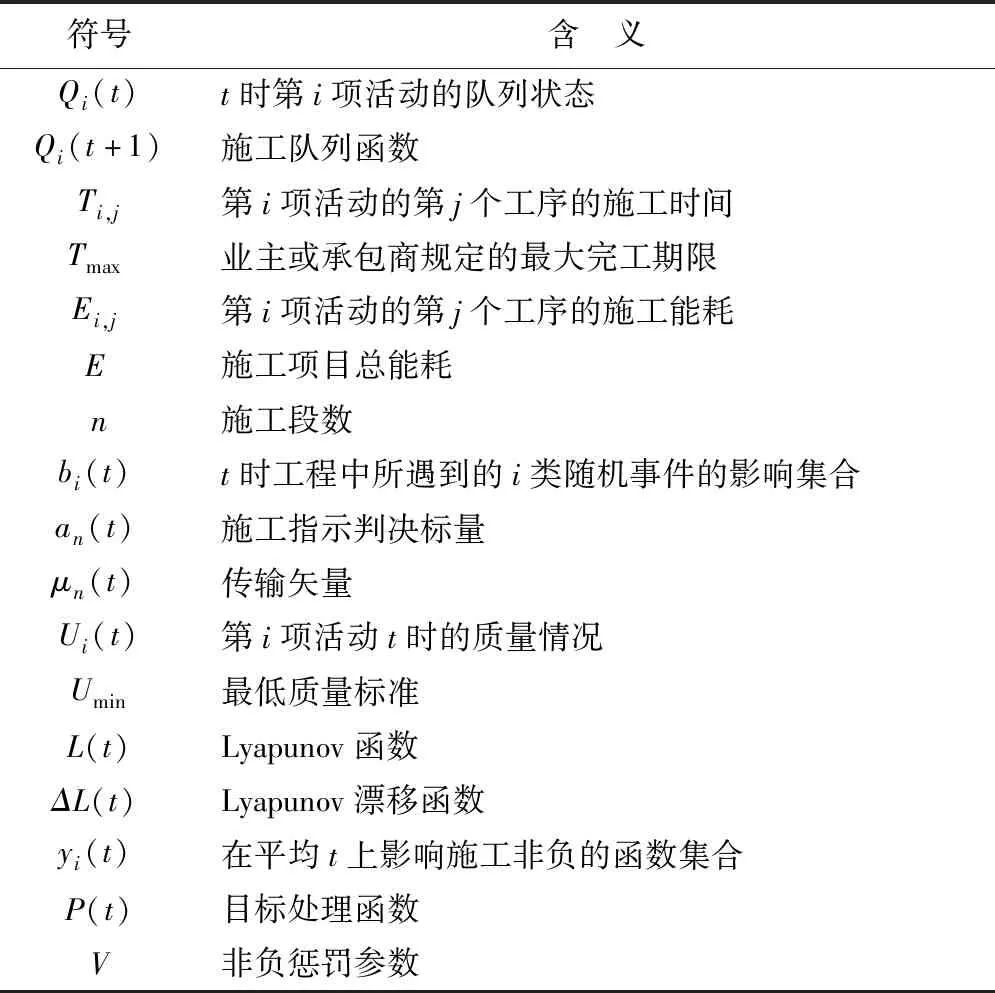
表1 主要符号注释
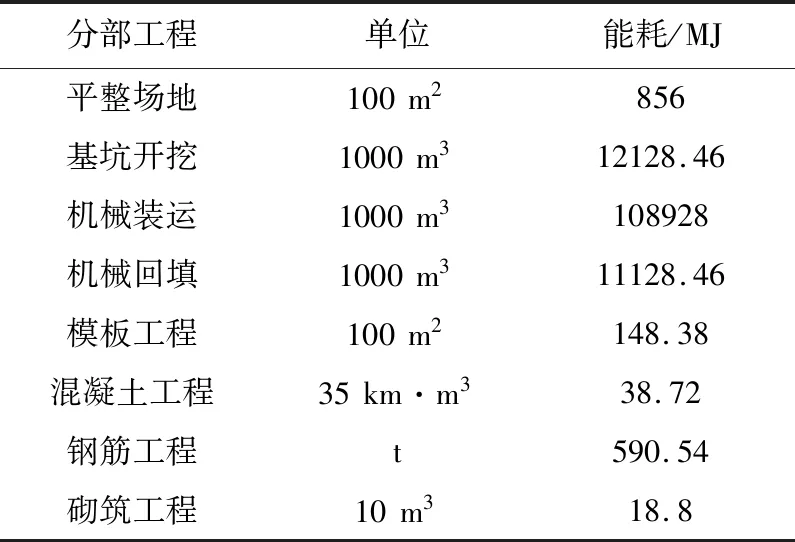
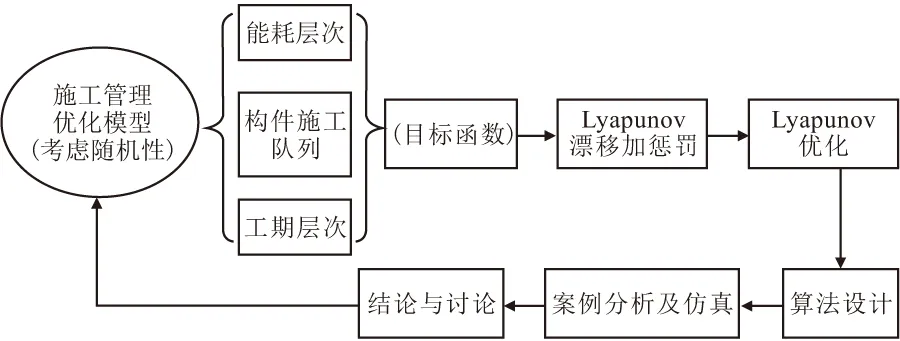
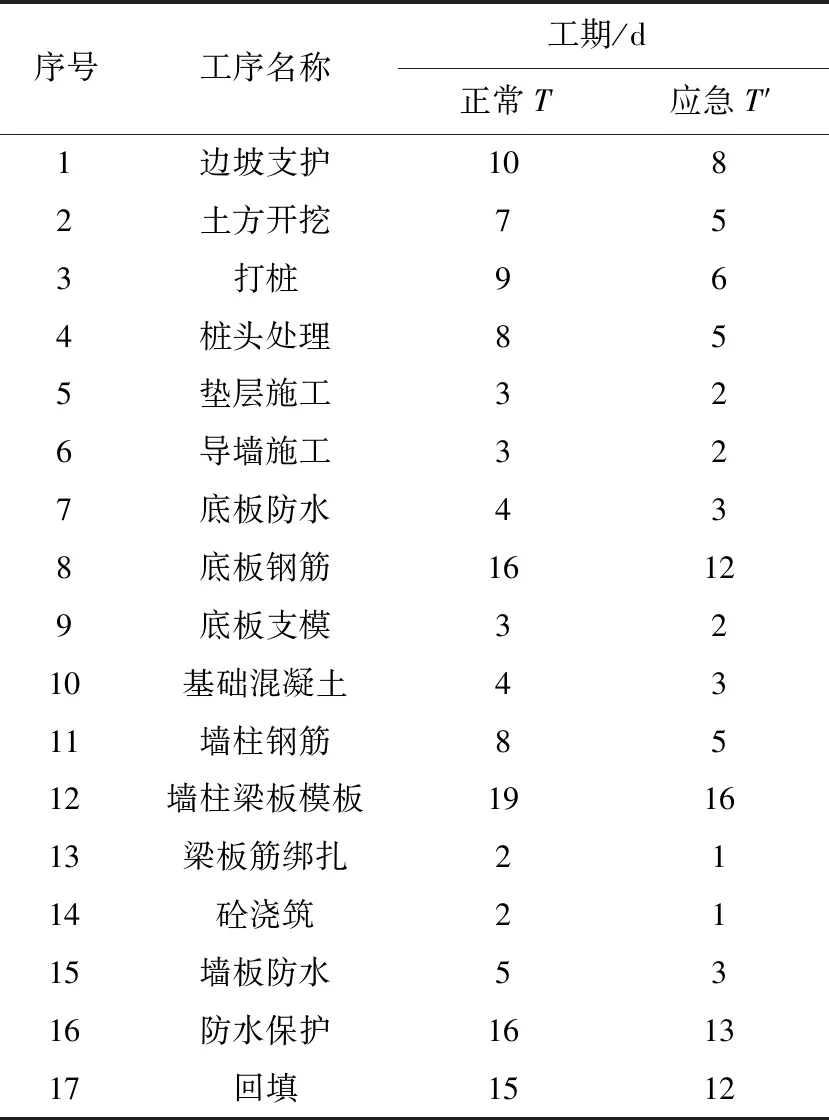
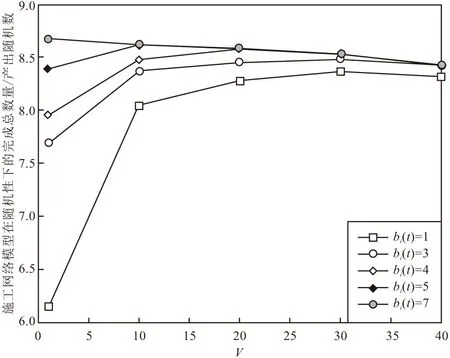
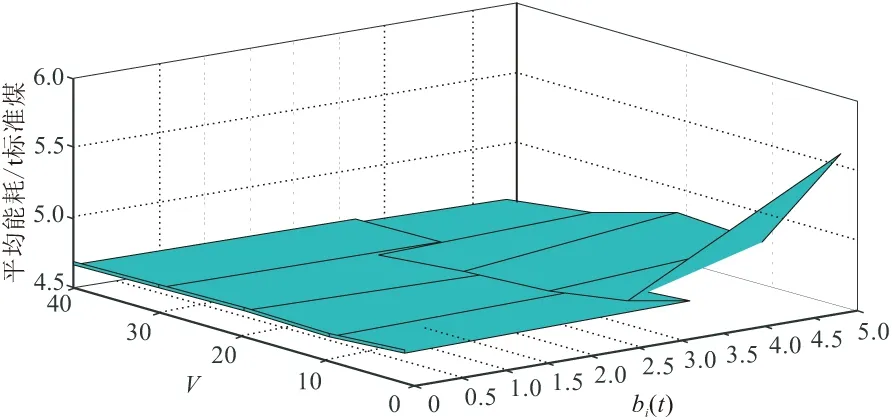
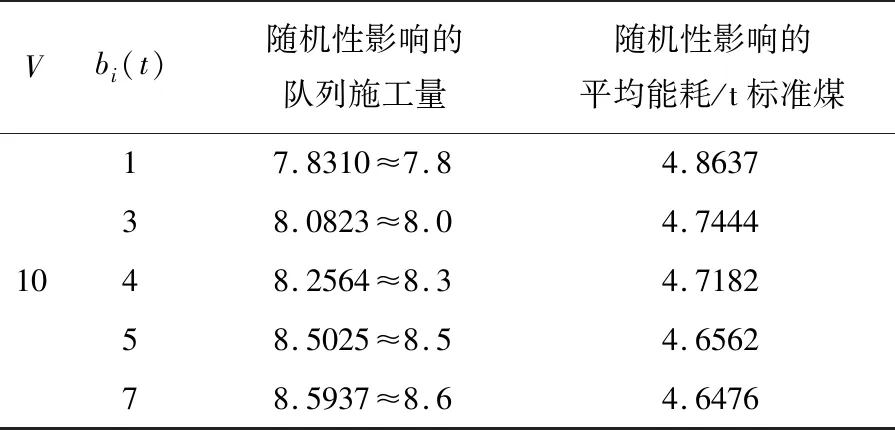
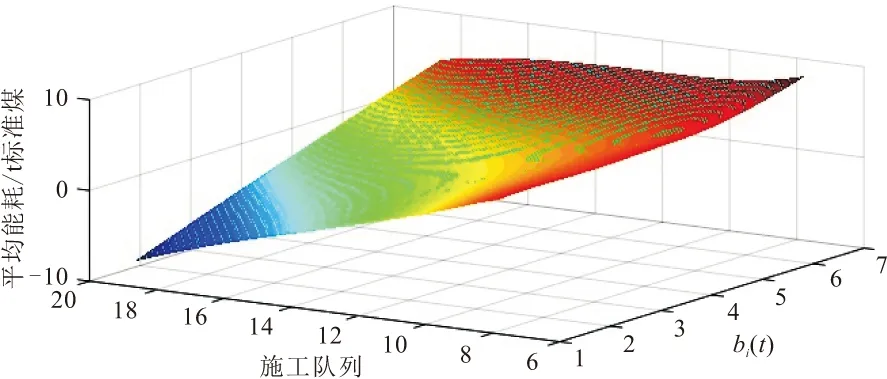
记C=(N,L)表示以N0(开工)作为施工队列的起点,经过施工队列通道的数量为L(l1,l2,…,ln),以Ne(竣工验收)作为施工队列的终点,建立以N1(土方工程)、N2(基础工程)、N3(主体工程)、N4(装饰装修工程)为工程信息节点的施工队列单向传输模型;同时,记工期为T,能耗为E,将各子工序在单位时间槽内的实时状态信息表达出来,其中,用Li+1(L1,L2,…,L5)表示各施工节点前后顺序的传输路径,i+j×10t来表示t时内的施工队列数据状况,i∈[1,10],i=10表示施工队列结束,i为工序数,j为对应i的施工技术,将施工过程数据化,设Umin为各阶段施工的最低完成质量,当i工序完成并且Ui(t)>Umin时,i+1工序的开工条件满足要求,当i工序完成但是Ui(t) 图1 施工队列模型示意 (1)每项活动的不同工序自由选择,以便编排施工队列; (2)施工顺序是单向的; (3)由于实际施工过程中具有随机性和不可预估性,故单位时间内的施工状态和能耗均不同,并且具有随机性,根据算法本身的特性,不需要预先知道施工期内随机性事件的概率分布; (4)在本文中做如下规定:将0 (5)本文的能耗统计是基于同一个工程进行的。 (1)将工期变量进行统筹安排,以每工日为单位建立时间槽t,构建施工进度平行计划:T,T′。 (2)将施工期的过程项目在单位t内进行编排,t是正整数,由于整体工期受合同的规定时间限制,因此,其范围如下: tmax>t∈[1,2,…,n] (1) (3)划分施工节点:N0,N1,N2,N3,N4,Ne。 Ni∈(N0,Ne) (2) (4)施工指示判决标量:an(t)∈[0,1],n∈N。其中,an(t)=1表示该工序完成进入下一个工序施工;an(t)=0表示该工序未开始。根据施工进行程度将an(t)划分为0,0.1,0.2,…,1的11个状态与上文提到的阶段完成质量U的情况共同表示某个施工阶段的实时信息,an(t)=[a1(t),a2(t),…,aN(t)]表示在t内的施工指示判决标量,并且定义传输矢量: μ(t)=(μn(t))|n∈N (3) 式中:μn(t)为进入到下一施工阶段的数量,使得0<μ(t)<μmax。根据以上信息和问题表达,构建施工队列,将施工组织设计的流水施工方案规定的施工工序n放入单位台班t内,排成可以根据实际状况进行随机资源分配的施工队列,并且施工队列的实时更新如下: Qi(t+1)=max[Qi(t)-μn(t)bi(t),0]+ an(t)μn(t),Qi(0)=0,0<μ(t)<μmax, 0≤bi(t),U>Umin (4) 式(4)右端包括两个部分,分别表示考虑到了bm(t)的影响和未完成工序传输量。 根据an(t)指示,工序衔接数量的实时状态。bm(t)=(b1(t),b2(t),…,bn(t))为第m类别随机性事件的n级影响程度下所需要决策的实时工序变量。将施工中的随机性数据化,对抽象的施工期随机性事件进行处理,产出随机的数组来模拟实际情况。 本文将工期函数划分为三个部分寻解:施工过程工期Ti、流水间歇工期Tz和验收时间Ts。根据实际施工情况进行如下分析。 施工过程中,在预估时间及成本条件下,Ti太小会涉及质量问题,Ti过大,则会涉及到赶工期的问题,意味着长时间占用人员、机械,因此会导致能耗和成本的增加,故工期要在Tg下找到一个平衡值,来规范工期的长短。因此,存在一个最小的施工过程时间,记作ti,min,因此规定ti,min (1)施工项目过程工期Ti(各个施工段的工期),由于该部分工期不是主动的能变值,因此在这方面做简单的累加: (5) (2)流水间歇工期Tz: Tz=nti (6) 为了方便计算,按施工经验,取ti=2 d。 (3)根据施工现场的实际竣工情况来确定的验收时间Ts。 综上,得到工期的权值函数T(t): (7) 式(7)右端包括三个部分,分别表示:施工顺利衔接所用的工期、施工中所耽误的工期、验收时间。 本文考虑施工过程总能耗Ep,在计算上会减少大量不可估计的数值。为方便计算,利用施工工序能耗估算法及施工现场实测法进行统计。能耗统计主要受到四个方面的影响:自然条件、机械效能、技术因素和管理水平。注意,在统计机械效能过程中,气温与海拔会对机械产生较大的影响,在本文的计算中均取中国内地施工标准值。因此,本文将施工能耗划分为以下三个方面,并且做了相关的现场统计。 (1)施工过程能耗E1 (8) 式中:Ni,j为第i项活动的第j道工序;P为一台机械的耗油率(比油耗),P=Tn/9550;I为一台设备电能消耗率,I=8NK1K2K3/K4,电能利用系数K1∈(0.6,0.8),时间利用系数K2∈(0.6,0.75),损耗系数K3=1.05,电机在满负荷时,有效利用系数K4=K1[30];t为设备工作时间,按统一规定,一个台班为8 h;βEi,j为第i项活动的第j个工序的特殊能耗,考虑到其影响的比重,β∈[0,1]为权衡系数。 表2是在施工现场实际勘察后计算整合起来的分部工程能耗统计表,并且以此作为后续仿真参考。 表2 施工各分部工程能耗统计 (2)施工生活区能耗E2 生活及办公区的能耗均取定额量,为了确保精确性,以实际统计值为准,单位统一为热量单位J。由于部分能耗不易被统计出来,用理论计算值能耗作为参考,表3为施工过程中的主要辅助能耗统计。 表3 施工过程中辅助能耗统计 (3)施工后期废弃物处理能耗E3 本部分能耗以往在竣工前后产生,为了方便审查验收,施工单位会组织机械处理施工后的场地,但是在实际工作中这部分能耗时常被企业忽视,本文查询了施工现场中常用垃圾货物清理车的物理标量及能耗定额,表达式如下: (9) 式中:et为运走单位质量,单位时间、单位距离的能耗;mi为垃圾的质量;l为安排清理废弃垃圾时所运输的距离,是根据施工现场管理安排的,一般取固定值。 综上,得到施工期能耗的权值函数E(t): (10) 式(10)右端包括三个部分,分别表示:施工顺利衔接的能耗、施工中耽误工期的能耗、废物处理的能耗。用施工指示判决标量an(t)来权衡各部分的问题。 (1)利用前文所构建的施工队列函数与工期内能耗函数进行处理得到目标函数。 (2)引入Lyapunov优化算法:1)构建虚拟施工队列依次进行调度;2)将施工队列函数导入二次Lyapunov函数;3)将2)进行漂移处理,带入惩罚项及惩罚参数V,得到目标函数的Lyapunov drift-plus-penalty表达式。 (3)经算法运行后,分析惩罚参数V和施工期随机性事件参数bi(t)对施工期能耗的权重影响与措施。 模型设计流程如图2所示。 图2 模型设计流程 2.2.1 虚拟施工队列 假设虚拟施工队列的积压随时间t的关系满足下式: Qi(t+1)=max[Qi(t)-μ(t)bi(t)+ δQi(t),0] (11) 式中:Qi(0)=0;δQi(t)是根据Qi(t)实时状态可调的参数,当Qi(t)>0时,δQi(t)取值影响随机情况下的延误工期和优化的目标函数,本文Qi(t)>0是根据随迭代次数的增多而变化的,可以用来计算在t内的Lyapunov漂移边界: Qi(t+1)2=max(Qi(t)-μn(t)bi(t)+δQi(t)>0)2 ≤(Qi(t)-μn(t)bi(t)+δQi(t)>0,0)2 (12) 2.2.2 施工排队网络的Lyapunov漂移 在离散的单位时隙t内进行网络排队,在施工期,有N个工序,定义工序的虚拟队列积压量为Qi(t)={Q1(t),Q2(t),…,Qn(t)},对于每个时隙t内的所有队列大小平方和后取1/2,由此,定义二次Lyapunov函数: (13) 用式(13)函数来表示排队网络的队列积压状态,是一个标量。 定义Lyapunov漂移为两个相邻时隙内的二次Lyapunov变化量: ΔL(t)=L(t+1)-L(t) (14) 据施工队列及虚拟的施工队列的实时更新可得: ΔL(t)=L(t+1)-L(t) (15) ΔL(t)=L(t+1)-L(t) (16) 式中: 因为在时隙t+1内完成的工序和将要开始的工序数量积压是有界的,因此一定存在一个大于0的常数B使得施工队列和虚拟队列的向量θ(t)∈{θ1(t),θ2(t),…,θn(t)},在时隙t满足E[B(t)|θ(t)]≤B,对ΔL(t)可以得到有界的Lyapunov漂移的条件期望: E[ΔL(t)|θ(t)]≤B+ (17) 使其满足,对实数ε>0,满足 E[μn(t)bi(t)-δQi(t)>0|θ(t)]≤-ε (18) 2.2.3 施工排队网络的Lyapunov漂移加惩罚 (1)Lyapunov漂移加惩罚理论 将Vp(t)引入漂移项当中,使惩罚的函数p(t)接近最优,得到相应的平均队列大小。因此,这里定义施工队列的控制状态的最小化如下面的漂移加惩罚表达式: ΔL(t)+Vp(t) (19) 式中:V为非负权衡值;p(t)为在时间平均状态下的惩罚函数,假设p(t)是由其他R个yi(t)时间平均函数的集合约束,可以选择不同的权值V,使得惩罚函数达到最优,该方法用于施工模型中,不需要知道施工工序某时刻的完成量和是否处于正在验收状态的概率分布,分析式子,当V=0时,漂移加惩罚方法则转化成最小Lyapunov漂移算法。当V>0时,表示在算法控制中增加了权重参数,权重队列的增减和最小化目标函数之间的平滑,V值越大,说明队列等待数量越多,稳定性会有所降低,目标函数的权重越大。 (2)漂移加惩罚的表达式 由于保障队列的稳定,定义Lyapunov函数L(t),对等式的两边取平方的形式,得到队列的边界: Qi(t+1)2≤(Qi(t)+yi(t))2 =Qi(t)2+2Qi(t)yi(t) (20) (21) 将ΔL(t)代入式(21),得到: (22) (23) 再将Vp(t)加入到不等式两边,在每个时间槽t内,观察当前队列状态采取惩罚措施以控制最小化的drift-plus-penalty界限,得到漂移加惩罚表达式: Θ(t)=ΔL(t)+Vp(t) (24) 2.2.4 施工期E(t)的权衡管理 由于实际施工项目的工期、能耗单位和计算方法的要求存在差异,故要采取权重的处理方式,将多目标量进行无量纲化处理: (25) (26) S(t)=log(αST(t)+(1-α)SE(t)) (27) 为了直观地将数据表达及方便计算式(28),定义log(x)为凸函数,α为权重系数,并且0<α<1。由于能耗和工期各自的权重函数里已经考虑了控制变量对各自的影响,因此为了方便计算,工期和能耗的权衡目标函数不做重复参数的迭代,只需做目标函数中参数的权衡。 综上所述,算法设计如下: 漂移加惩罚算法的主要思想为在满足一定平均时间的约束下最小化惩罚函数,首先在时隙t内选择惩罚函数所包含的事件向量和控制决策函数,在施工队列模型中,由于施工模型不同于通信网络所存在的队列稳定、时变收敛和数据参数广泛等问题,使得运算具有简单性,由施工期能耗和工期所联合控制的施工函数S(t)为目标函数,最终将目标函数寻找一个控制策略来最小化如下问题: Θ(t)=ΔL(t)+VS(t) ≤B(t)+VP(T(t),E(t))+ (28) (29) Θ(t)=ΔL(t)+VS(t) VP(ST(t),SE(t))+ (30) yi(t)=Yi(ST(t),SE(t)) (31) p(t)=P(ST(t),SE(t)) (32) (33) 约束条件为U>Umin。 上式yi(t)是在平均t内的影响函数的集合,是非负的。根据施工模型可知,yi(t),S(t)都是有界的,其中E(x)表示对x求数学期望,U>Umin时,保证施工质量。 现有河北省秦皇岛市某小区工程,住宅部分为剪力墙结构,地下车库为框架结构,具体工程概况如下,根据算法设计部分的目标函数及相关参数仿真设计如表4所示。 表4 仿真设计参数 (1)建筑面积:175445.63 m2(地上建筑面积约144820 m2,地下建筑面积约30625.63 m2)。 (2)目标工作:由六栋地上建筑(38#,39#,40#,41#,42#,43#六栋楼,30~32层加地下室3层)和一层地下人防车库组成。 (3)工期要求:2017.6.15—2018.9.30(共472 d)。 (4)能耗统计:截止到2018年9月30日,项目共消耗电量41.2万度,汽油用量3.66 t,柴油用量8.64 t,综合能耗0.0098 t标准煤/万元,低于本年分解指标0.0326 t标准煤/万元(可比价)。表5~7为二—四季度(按300个台班)的主体及装修施工阶段总能耗统计表与其他研究数据。 表5 施工现场主体施工阶段能耗统计 (5)其他:建筑垃圾处理阶段,安排清理废弃垃圾时所运输的距离l=1210 km,使用常规的垃圾压缩车,容积8 t;竣工验收时间约为10 d,包括合同签字;bi(t)=1,3,4,5,7;V=10,20,30,40;1 MJ热量按0.03412 kg标准煤计算,单位取t标准煤。 表6 项目部所统计的2018年二—四季度主体施工及装修阶段相关指标 表7 工程项目的工期及工序安排 本文在设置随机性bi(t)的取值问题解决如下:在三个影响等级中均匀取值,分别取随机性bi(t)=1,3,4,5,7,其中m是随机事件的类别。通过非负的惩罚参数V和随机性影响等级参数对施工网络模型的影响,仿真结果如图3~5所示。 图3 参数V和随机性bi(t)对施工网络模型的传输完成数量的影响 图4 参数V控制下对施工队列模型单位t内的平均能耗影响 图5 参数V、随机性bi(t)和施工队列平均能耗关系 图3通过调节参数V来控制因bi(t)影响的施工工序的数量,可见V由10到40的惩罚力度很大,在考虑随机性事件发生条件下不耽误施工或者将其影响降到最低。如图3,bi(t)>3时,说明某一随机性影响在中等及以上,会对施工有较大影响,但通过调节参数V的大小来增加对这一随机性的惩罚,即对施工中的随机性进行预估处理,可以降低该事件对施工工序阻碍的影响,间接改变工期,这是符合实际要求的。 通过计算机仿真实验,利用rand(x)函数产出所要模拟随机性事件的影响等级对实际施工过程的影响,观察算法的惩罚参数V和随机性事件影响的等级参数bi(t)对目标的作用,分析结果如下: 根据图3,4可知,bi(t)的值增大,说明随机性能影响增大,严重会阻碍施工,会降低能耗值,但这并不是我们在实际工程中想要的结果,所以,调整惩罚参数V来降低能耗变化,但是增加了惩罚项的队列堆积,会延误施工进度,增加工期,V在0~10之间的影响最为明显,对施工中的随机性进行预估处理来应对随机性对施工的影响。为了突显仿真结果,取V=10时,能耗与施工队列的数值如表8所示。 表8 V=10时对施工网络模型性能的影响 由表8可知,同一非负惩罚参数V条件下,对随机性影响的完成施工量和随机性影响的平均能耗的权重影响是由bi(t)来决定的,如图6所示。bi(t)>7时,无明显影响,因为此时随机性偶遇事件对施工的影响很大,需要采取对应方案处理。V代表着采取的处理措施及力度。 图6 V=10时不同bi(t)下的施工队列和平均能耗关系 当bi(t)对施工期的影响程度逐渐增加时,可以看到平均能耗随之增长,为了惩罚多余的能耗浪费,此时惩罚参数V亦随之增加,目的是针对过多的能耗量实现对bi(t)的惩罚,减小目标函数中SE(t)的值。当V在同一个值的状况下,表示惩罚效益不变,随着施工队列的进行,bi(t)取小值,而施工队列已经进行到一定程度,能耗值不可能为负数,说明三者之间必然存在一个权衡范围,因此在上述V=10的研究过程中,bi(t)和Qi(t)的值符合仿真设计得到的结果。 施工期随机事件对能耗的影响,主要研究的是极端天气对施工进度和能耗的影响,可以结合人工智能技术实现学科的互融性和专业交叉的应用,通过引入大数据的思想采集50年内的某地区施工日志、环境数据和地区法规来约束bi(t)的函数关系,提高算法精度和速度。将施工期随机性做精准的函数表达与定义是下一步要解决的重要工作。 由于虚拟队列的构建、相关参数的选取和数量级范围与施工模型存在差异,因此本文在算法设计上进行了修改,选取合适的参数和符合实际施工的约束条件,避免数据处理的计算错误;然而,这个模型也有一些局限性,在算法仿真中很难克服随机性中级数范围的取值问题,因为该算法的自身随机包容量很大,搜索结果可能存在不稳定性,针对这个问题,作者正在努力寻求改进的方法。 本文利用Lyapunov动态队列控制技术建立施工队列模型对施工能耗进行权衡与分析,得出以下结论: (1)通过对国内外文献的查阅与施工现场的调研,发现了目前建筑企业的施工能耗管理存在重视程度不足和分析片面等问题,因此建立了施工队列模型,对施工能耗进行系统的权衡分析。 (2)利用Lyapunov控制动态队列技术的优点和土木工程施工的特点,将两者巧妙结合,实现智能化施工,本文模型的明显优越之处是不需要知道施工随机事件的概率分布信息。 (3)通过实证分析,验证了该模型的适用性和可行性,根据仿真结果对影响参数进行了详细分析,特别是惩罚参数V的影响,体现了该模型的应用价值,对建筑企业施工能耗的分析和控制具有一定的指导意义。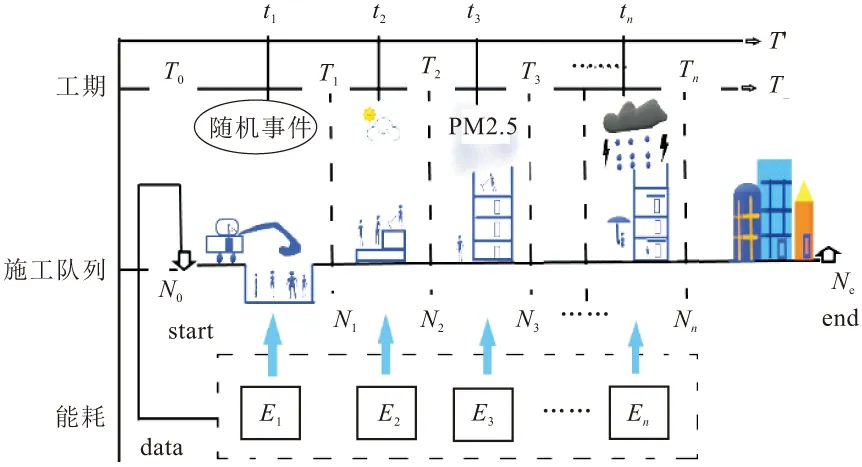
1.2 构建施工队列
1.3 工期模型
1.4 能耗模型

2 算法设计及求解
2.1 算法设计
2.2 相关理论与求解过程
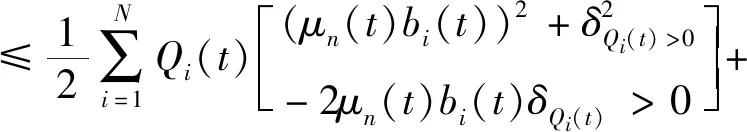
3 仿真与分析
3.1 仿真设计



3.2 惩罚参数V和bi(t)对施工模型的影响及分析

4 结 论

