城际高速铁路桥梁车行动力响应
周宏宇,袁 慧,麻全周,刘亚南,周 运
(北京工业大学 建筑工程学院,北京 100124)
近年来,随着我国工程技术的日趋成熟,铁路高速化尤其是客运铁路高速化已经是一种必然的发展趋势。然而铁路高速化发展的同时,也为工程结构带来了一定的考验。车速的提高,发车频次的增加,使得桥梁在高速行车荷载下产生的振动响应与中低速下会有所不同[1,2],因此,桥梁所受车行动力响应具备了新的研究价值。
车桥振动问题自1825年受学者们关注以来已有较长的研究历史,早期研究主要单独从理论分析、试验研究以及仿真模拟中的某方面着手[3~6],近些年研究者们常将它们结合使用。Ling等[7]基于耦合有限元多体动力学理论应用有限元模型预测了单跨直线简支梁桥在脱轨冲击下的动力响应;Olmos等[8]通过建立三维车桥系统模型研究了高速列车运行下桥梁的横向响应;黄文杰等[9]利用能量法建立车桥竖向振动系统方程后计算研究影响简支桥梁共振的主要因素;夏禾等[10]对秦沈客运专线24 m跨度的预应力混凝土简支箱梁进行了最高时速为321.5 km/h的列车动载试验,并依据现场试验数据分析得到了桥梁的动力特性和振动性能。时瑾等[11]通过解析推导研究了等跨桥梁与二轴车相互作用的共振机理和条件,并结合重载铁路工程实例加以验证。李慧乐等[12]采用3种常用的车桥动力响应分析方法对两座计算跨度为32 m的简支T梁进行了应力动力响应计算,将计算结果与现场实测数据对比以验证三种方法的适用性。孟令强等[13]对某一T型桥梁结构开展了动、静载试验,从梁体变形、冲击系数、横向振动等多个角度评价了桥梁的刚度、强度。欧阳冲等[14]运用MATLAB建立了以梁段单元为基础的车桥计算程序,通过数值模拟研究了不同时速下桥梁横、竖向振动的差异性;肖烨等[15]基于多体动力学理论和有限元法建立了车-轨-桥精细化模型,并结合现场动载试验研究了30 t轴重列车作用下桥梁的动力响应。
京津城际铁路正是我国第一条具有完全自主知识产权、世界一流水平的高速铁路,于2018年8月再次提速至350 km/h。本文在此工程背景下,通过建立基于Timoshenko理论的车-轨-桥三维简化模型,在确保建模正确情况下进行实例仿真,分析高速列车下梁体各指标的动力响应变化规律,并通过应力敏感度研究确定其薄弱部位。
1 模型建立与验证
1.1 有限元模型的建立
以京津城际铁路高架桥为工程背景,分别建立了32 m桥梁模型、轨道模型和车辆模型,再将各部分子模型进行装配组成了车-轨-桥动力模型。桥梁模型为双线箱型简支梁,采用基于Timoshenko梁理论的Beam188单元,将桥梁的二期恒载作为均布质量分配到相应的桥梁单元中去,为追求合适精度,选用了人工指定网格的方式划分单元,共128个。桥梁跨度32 m,其余参数如表1所示。

表1 桥梁模型几何及材料参数
车辆模型由“和谐号”CRH3动车组忽略外观形状建立得到,每列8组编车,根据连接方式每节车厢分为两大组成部分:转向架和车身,其中转向架由侧架、摇枕、轮轴、轮对、悬挂系统构成;转向架中轴距、定距分别为2.5,17.5 m,轮对、转向架、车体的质量分别为2.4,3.2,40 t;建模时主要采用了Beam188单元(车身、摇枕、侧架、车轴)、Combin14(悬挂系统)和Solid45(车轮);基于部件刚性、轮对密贴性、运动方向简化性等假设,通过约束车体、转向架、车轮中的部分不必要的刚体运动自由度后,该车辆模型中的每节车厢各计16自由度,划分为231个单元。车辆模型技术参数作如下取值:车体、转向架的点头惯量分别为5.47×105,6.8×103kg·m2;一系悬挂的横、垂向刚度分别为9.8×105,1.18×106N·m-1;一系悬挂的横、垂向阻尼分别为3×103,1.96×104N·s·m-1;二系悬挂的横、垂向刚度分别为1.59×105,1.89×105N·m-1;二系悬挂的横、垂向阻尼分别为2.94×104,4×104N·s·m-1。
轨道模型为CRTSII型无砟轨道,自上到下主要由钢轨、扣件、轨道板、砂浆层和底座板组成,钢轨将外荷载作用(如列车荷载、风荷载等)经由扣件、轨道板、砂浆层、底座板传递给桥梁;主要采用了Shell193(底座板、轨道板)、Solid45(钢轨)和Combin14(砂浆层、轨道板、钢轨间扣件),共计16646个单元。其中砂浆填充层30 mm厚,钢轨弹性模量取206 GPa,该子模型的其余材料及截面特性参数如表2所示。ANSYS中的MPC (多点约束方程) 技术为解决不同类型、不同大小网格单元的连接问题提供了便利,通过引入MPC184单元和相关接触选项的设置,基于节点建立连接区域的联系使得所需连接的单元节点具有一致连通性,不同材料属性、网格划分间的各部件采用MPC技术进行装配以完成力的传递;梁和轨道板间也通过MPC技术连接成整体;车轮和钢轨之间的接触连接采用位移-接触法模拟,即选用合适的接触单元与目标单元使得上部移动的车轮与其所到之处的钢轨之间建立接触关系,并根据行车速度、单元长度控制动力分析计算的时间,对车辆系统施加D命令使其在行车方向上产生水平位移来模拟列车的行进。该仿真基于接触不分离假定,接触类型选用面-面接触。

表2 轨道系统几何参数
1.2 有限元模型验证
为验证建模的正确性,首先对按原型梁进行1∶11缩尺设计的模型梁进行模态试验,所试验的缩尺梁如图1可示;同时在ANSYS中对原型梁进行模态分析,应用结构动力试验中的相似准则[16],在主要考虑几何相似、材料密度相似和弹性模量相似的基础上得到固有频率相似系数0.0883,以该值将模型梁的试验值转换成原型梁模态试验值再与模拟值比较。
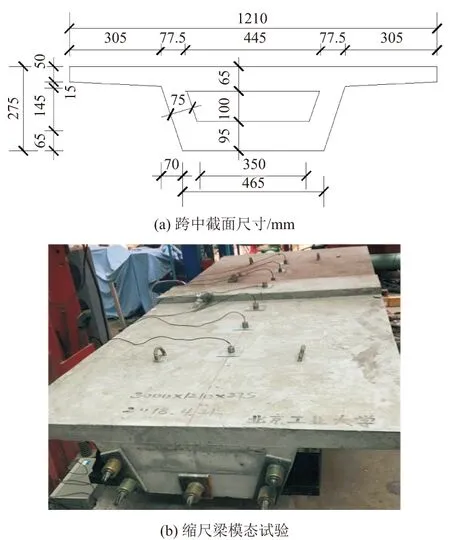
图1 缩尺模型梁
对比发现,试验推导值和模拟值最大误差为7.195%,出现在第四阶频率,在可接受范围内,试验结果与模拟结果见表3。
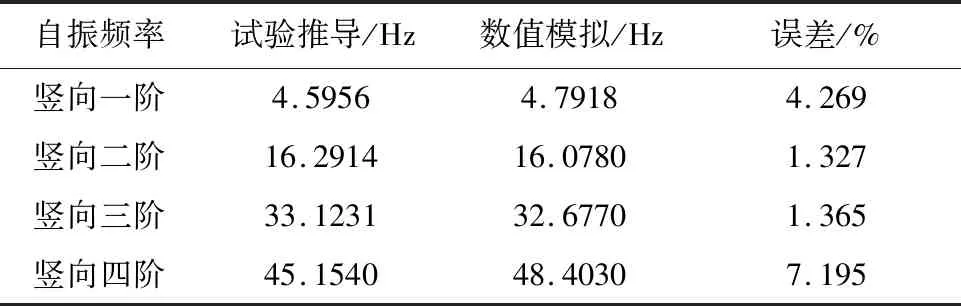
表3 桥梁自振频率对比
2 京津城际铁路高架桥实例分析
结合京津城际高速铁路工程背景,分别对双线桥单线行车、双线桥双线同向行车、双线桥双线对向行车三种工况下的车行响应进行了数值模拟,研究车桥相互作用下的梁体响应。其中双线同向行车工况由于在实际工程中罕见,在本文中仅将其作为对照工况进行分析。动力计算时选用ANSYS的瞬态分析模块,利用ANSYS强大的APDL功能,通过编写命令流使得完成的模型从/PRE7切换至/SOLU模块,设置计算类型为瞬态分析,采用Newmark积分法,时间积分步长结合单元长度和所关注的最高阶自振频率取0.0005 s。
图2为8组编车的CRH3动车组和32 m的简支箱梁、轨道系统通过建立面-面轮轨接触关系进行组装后的三种行车工况模型图。

图2 三种行车工况
2.1 梁体位移
为叙述方便,本文均将时程曲线的横坐标转换为列车荷载的位置(列车桥头相对于进桥梁端的距离),其本质仍为所研究的参数在时域上的变化。图3为350 km/h时速时三种工况的梁体位移响应。在单线行车荷载下,随着列车向出桥方向移动,位移变化趋势为谐波曲线,当列车车头距离进桥端约145 m时,桥梁跨中位移达到最大值;在双线对向行车荷载下,随着行车位置的变化,梁体位移的振动形状同单线荷载下的振动形状,跨中位移最大值发生在列车车头距进桥梁端140 m处;双线同向行车荷载下的梁体位移振动形状与前两种相同。
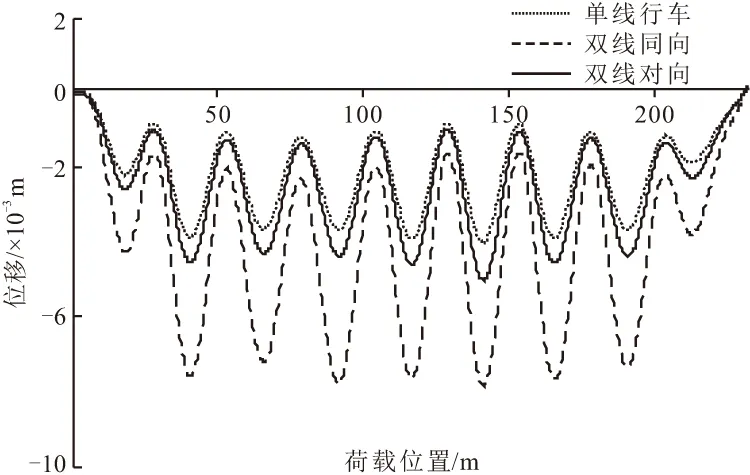
图3 三种工况梁体跨中位移响应
基于上述分析可知,三种工况梁体位移在时域上的波形变化是随机振动和衰减振动耦合的结果,且振动频率相同。由位移包络图图4可知,单线行车位移响应最小,双线同向行车时位移响应最大,单线、双线对向、双线同向的位移峰值分别为3.94,5.01,7.81 mm,且均出现在跨中,双线行车两种工况的位移峰值分别为单线行车时的1.27,1.98倍。
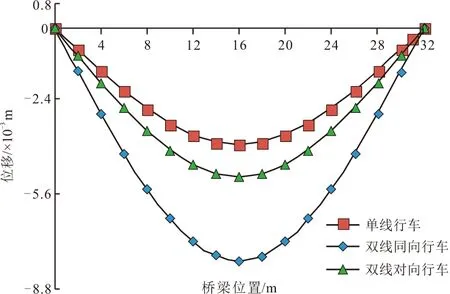
图4 三种工况梁体位移包络图
2.2 梁体弯矩
图5展示了三种工况下梁体跨中竖向弯矩在时域上的变化情况。竖向弯矩的振动波形与位移振动相似,单线行车时梁体跨中竖向弯矩最小,两种双线工况的梁体跨中竖向弯矩接近。由图6可知,三种工况的竖向弯矩最大值均出现在跨中,单线、双线对向、双线同向行车时梁体竖向弯矩最大值为16451,20971,32604 kN·m,双线同向工况约为单线工况的2倍。

图5 三种工况梁体跨中竖向弯矩响应
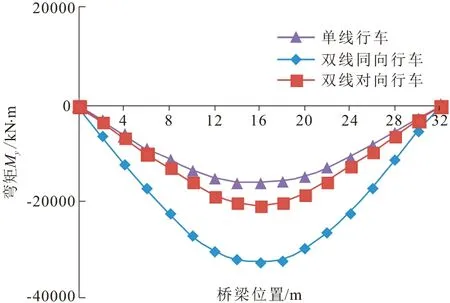
图6 三种工况梁体竖向弯矩包络图
图7展示了三种工况下梁体跨中横向弯矩在时域上的变化情况。横向弯矩的振动波形为锯齿状,由图7可知,双线同向时梁体跨中横向弯矩最小,单线行车和双线对向时的梁体跨中横向弯矩很接近,这与竖向弯矩响应规律不同,可能因为双线同向行车时的荷载完全对称的缘故。由图8可知,单线行车和双线同向行车工况的横向弯矩峰值均出现在桥端,而双线对向行车的峰值出现在跨中。单线、双线同向、双线对向行车时梁体横向弯矩最值为3898.48,349.88,2203.54 kN·m,单线工况约为双线对向工况的1.77倍。
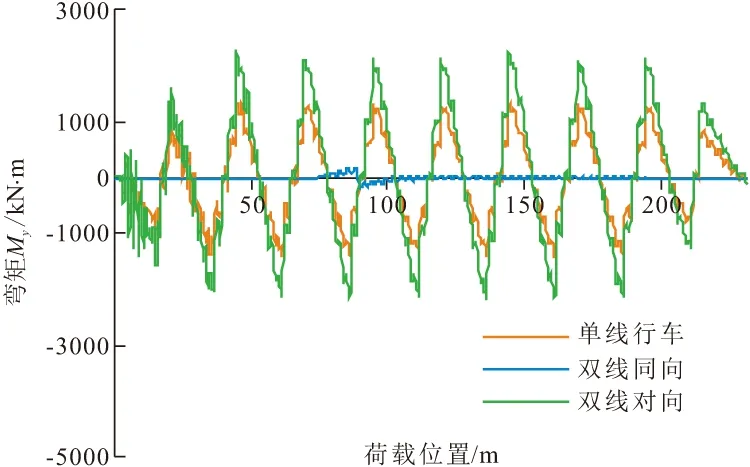
图7 三种工况梁体跨中横向弯矩响应
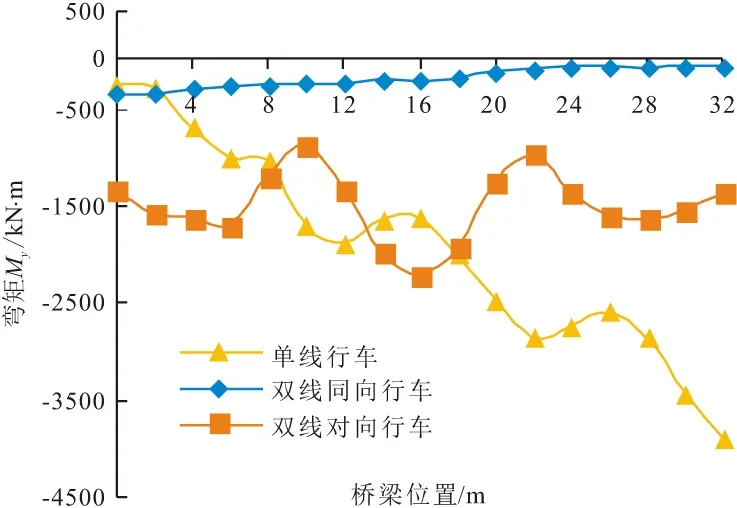
图8 三种工况梁体横向弯矩包络图
2.3 梁体剪力
图9为行车荷载下的梁体竖向剪力响应,单线行车和双线对向行车时的梁体跨中竖向剪力振动波形为锯齿形,而双线同向行车时的梁体跨中竖向剪力在时域上呈梳齿型变化,且数值较小,振动频率也与其他两种工况不同。图10为三种工况的梁体竖向剪力在各跨段的包络图,由图10可知,双线同向工况下梁体竖向剪力的包络线几乎将其余两种工况的剪力幅值包络在内,最大绝对剪力值为2094 kN。三种行车工况的竖向剪力峰值均出现在支座处。

图9 三种工况梁体跨中竖向剪力响应
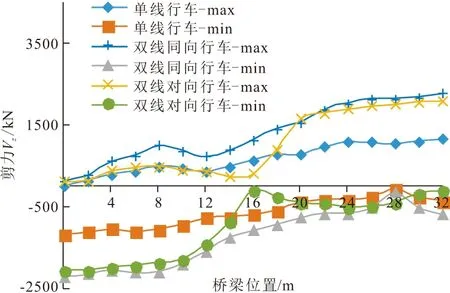
图10 三种工况梁体竖向剪力包络图
2.4 梁体应力
图11为单线、双线同向、双线对向行车时梁体跨中宽度右侧(单线行车时的荷载侧)弯曲应力,由图11可知,单线行车时弯曲应力在列车初上桥阶段振动幅值、振动频率均很大,双线对向行车时的梁体弯曲应力在某些时刻突增,三种工况中双线同向行车时的弯曲应力响应最小。图12为宽度方向右侧的梁体弯曲应力包络图,单线行车过程中弯曲应力峰值出现在跨中,双线对向行车时弯曲应力峰值分别出现在梁体3/8跨和5/8跨,双线同向行车时的弯曲应力峰值分别出现在支座处(压应力)、1/4跨至7/16跨处或3/4跨至9/16跨处(拉应力),单线行车时梁体顶部弯曲应力包络曲线几乎可包住其余两种工况。梁体左侧弯曲应力与右侧对称。

图11 三种工况梁体跨中+y侧弯曲应力响应
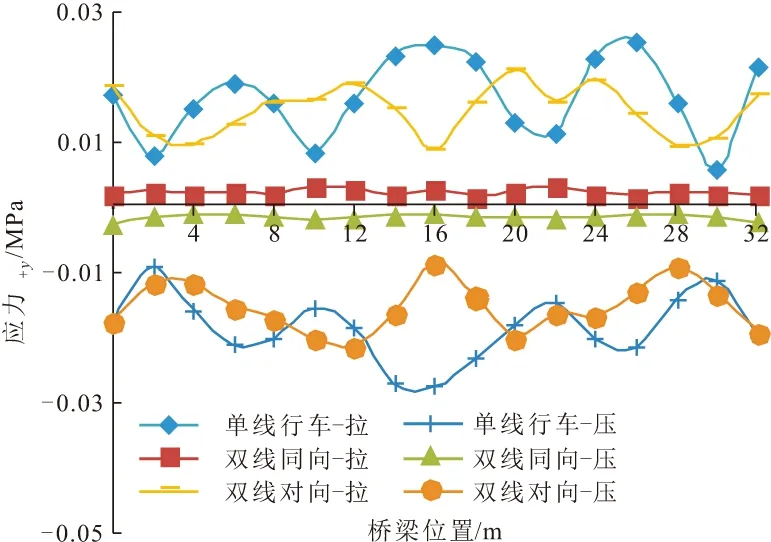
图12 三种工况梁体+y侧弯曲应力包络图
图13为单线、双线同向、双线对向行车时梁体跨中高度方向(梁体顶部)弯曲应力,其在时域上的振动波形与位移波形相似。由图可知,单线行车时的应力振动幅值最小,两双线行车时的振动幅值几乎一致。图14为梁体顶部弯曲应力在各跨段的响应最值,由图14可知,梁体顶部以受压为主,单线、双线对向、双线同向行车时的梁体高度方向弯曲应力最值均出现在跨中,压应力大小依次为1.18,1.51,2.34 MPa。

图13 三种工况梁体跨中+z侧弯曲应力响应

图14 三种工况梁体+z侧弯曲应力包络图
3 京津城际铁路高架桥薄弱部位
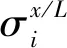
(1)
3.1 单线行车
3.1.1 横截面拉应力敏感度
单线行车梁体拉应力随横截面宽度的变化如图15,16所示,由图可知,单线行车荷载作用下梁体的拉应力由横截面跨中向腹板处逐渐减小,即越靠近横截面中心梁体应力敏感度越大。以梁体底板底部为高度初始位置,梁体拉应力随高度位置的变化如图17,18所示。由图可知,单线行车荷载下,梁体拉应力由底板向顶板逐渐减小,这符合受弯构件顶部受压为主、底部受拉为主的现象,即底板处的拉应力敏感度相对于横截面其他高度位置的更大。

图15 各横截面宽度处的梁体最大拉应力

图16 各横截面宽度处的梁体拉应力敏感度
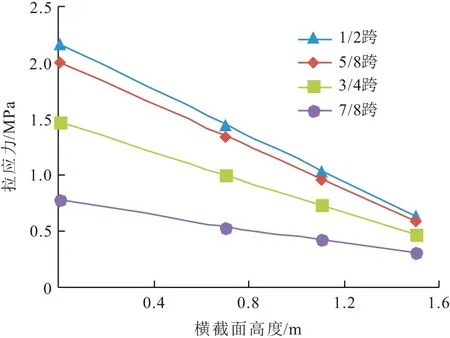
图17 各横截面高度处的梁体最大拉应力
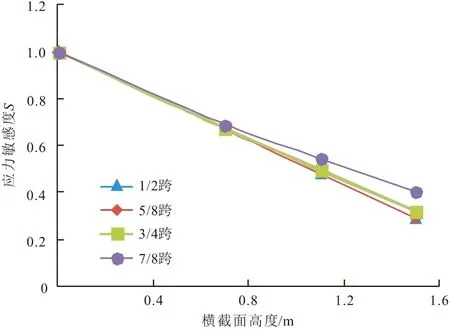
图18 各横截面高度处的梁体拉应力敏感度
3.1.2 不同跨位拉应力敏感度
图19,20为单线行车不同跨位处的梁体最大拉应力变化情况,图中横坐标为选取的观测点至梁端距离d与梁长L的比值,表示观测点所在梁上的跨段位置。由图可知,在单线偏载行车情况下,选取的几个典型跨段处的拉应力大小均由跨中向跨边减小,其中底板处减小的幅度最大,1/2腹板高处减小的程度最小;选取的横截面各节点的应力敏感度随着桥梁跨位的变化趋势很接近。
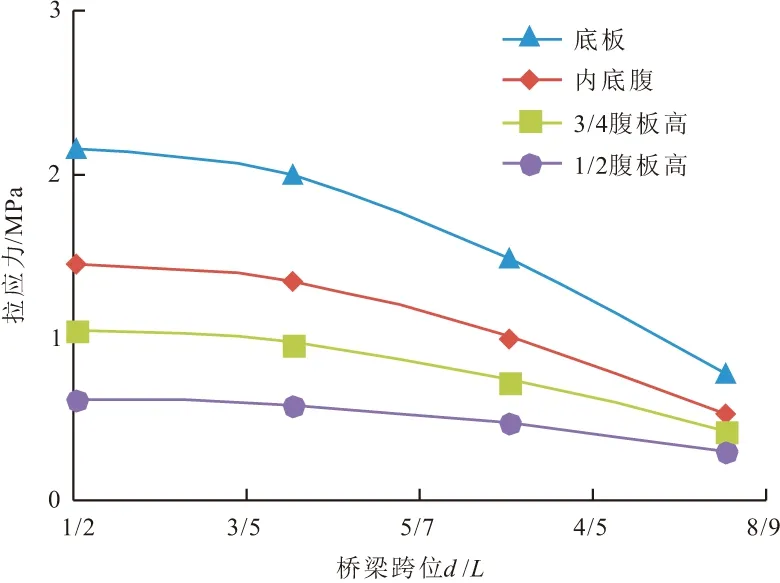
图19 不同跨位处的梁体最大拉应力

图20 不同跨位处的梁体拉应力敏感度
3.2 双线同向行车
3.2.1 横截面拉应力敏感度
图21,22为双线同向行车荷载作用下梁体拉应力随横截面宽度位置大小变化的情况。由横截面宽度中心向腹板,拉应力呈减小趋势,沿腹板厚度的拉应力变化率提高;该工况下的横截面中心拉应力敏感度总是大于沿宽度方向其他位置。

图21 各横截面宽度处的梁体最大拉应力
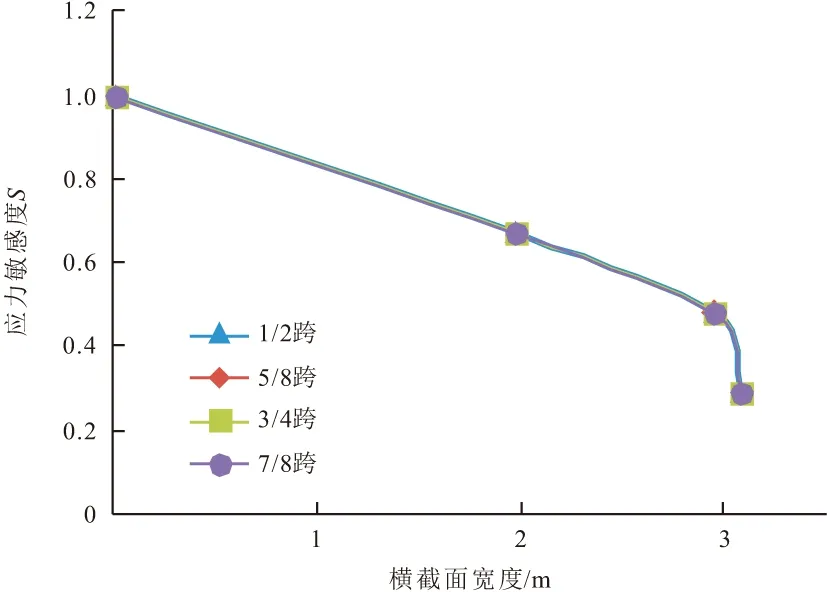
图22 各横截面宽度处的梁体拉应力敏感度
图23,24为双线同向行车荷载作用下梁体的拉应力随横截面高度位置大小变化的情况(以底板底部为横截面高度初始位置)。该工况下的拉应力大小由底板向顶板呈线性下降趋势,由图中线段斜率可知,跨中位置的拉应力变化率最大,跨边位置的拉应力变化率最小;梁体底板处的拉应力敏感度相较于梁高其他位置较大。
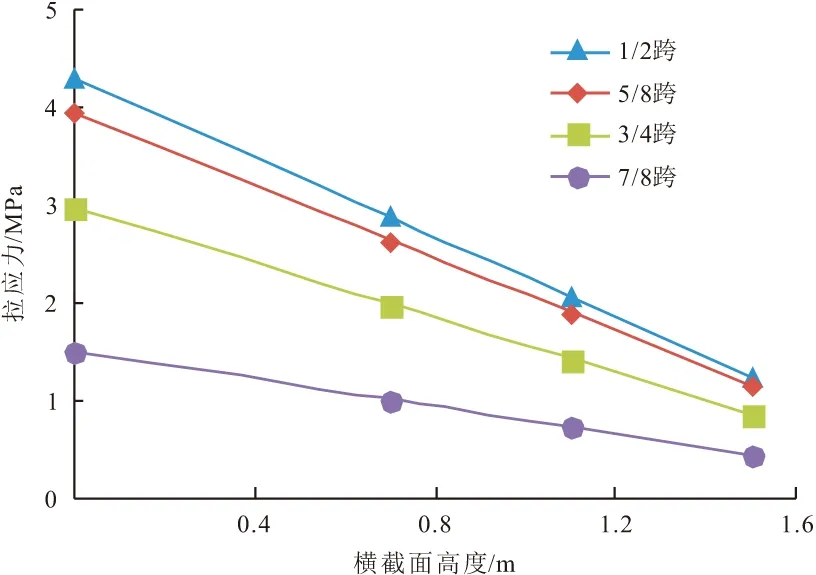
图23 各横截面高度处的梁体最大拉应力
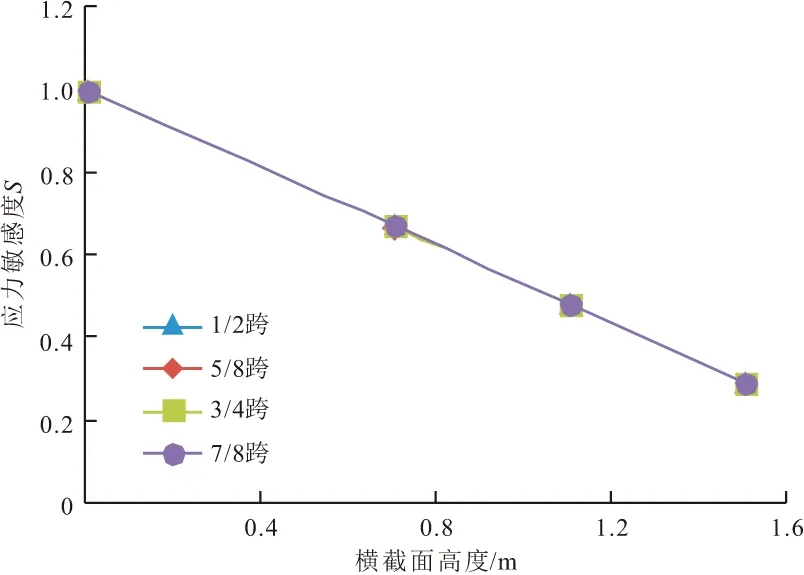
图24 各横截面高度处的梁体拉应力敏感度
3.2.2 不同跨位拉应力敏感度
由图25,26可知,在选取的几个典型跨段中,桥梁拉应力由跨中向跨边逐渐递减,底板的减小幅度最大,1/2腹板高处的拉应力下降幅度最小,但横截面上选取的几个节点相对于各自位置的跨中拉应力敏感度近似相同。
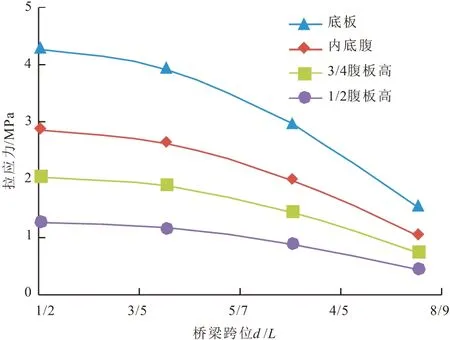
图25 不同跨位处的梁体最大拉应力
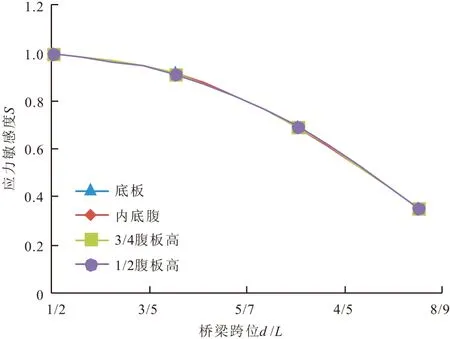
图26 不同跨位处的梁体拉应力敏感度
3.3 双线对向行车
3.3.1 横截面拉应力敏感度
双线会车荷载下梁体拉应力随横截面宽度变化规律如图27,28所示。由图可以看出,远离横截面中心处的梁体拉应力更小,沿腹板厚度处的拉应力下降速率更快;拉应力敏感度由横截面中心向腹板翼缘处逐渐递减。

图27 各横截面宽度处的梁体最大拉应力

图28 各横截面宽度处的梁体拉应力敏感度
双线会车荷载下梁体拉应力随横截面高度变化规律如图29,30所示(以底板底部为横截面高度初始位置)。由图可知,远离横截面中心处的梁体拉应力更小,拉应力由底板向顶板呈线性减小,即梁体底板处的拉应力敏感度最高。

图29 各横截面高度处的梁体最大拉应力

图30 各横截面高度处的梁体拉应力敏感度
3.3.2 不同跨位拉应力敏感度
图31,32为双线对向行车荷载下梁体拉应力随桥梁跨位的变化规律。随着梁体跨位由跨中向跨边变化,拉应力逐渐递减,其中底板拉应力减小速率最大,1/2腹板高处拉应力减小速率较小;截面不同位置处的拉应力敏感度一致,梁体跨中拉应力敏感度最大。
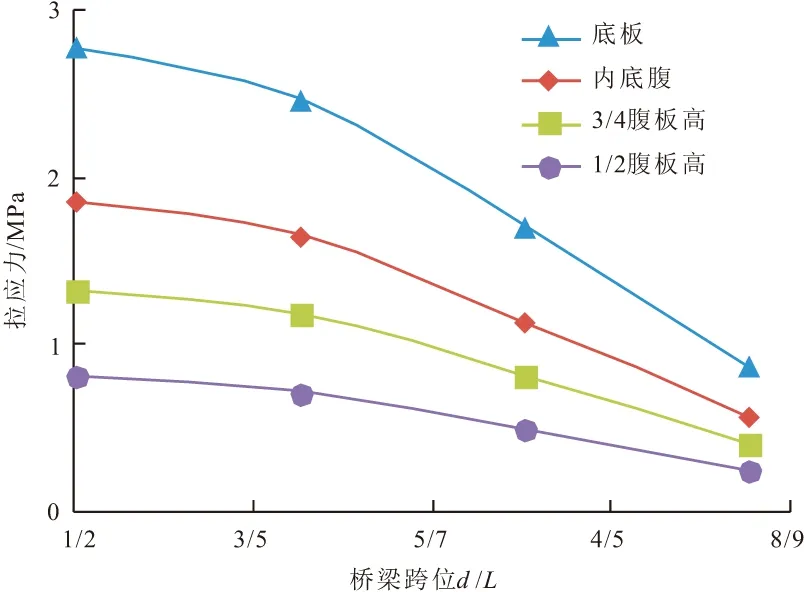
图31 不同跨位处的梁体最大拉应力

图32 不同跨位处的梁体拉应力敏感度
4 结 语
本文通过数值模拟对不同行车工况下的城际铁路高架桥的车行动力响应及薄弱部位进行了研究,得出以下结论:
(1)采用ANSYS中三维梁单元建立的桥梁模型自振频率与试验实测推导值的结果吻合较好,可认为此建模方法可行。
(2)京津城际铁路单线行车、双线同向行车和双线对向行车三种工况下的各分析指标响应峰值大小无统一规律,响应峰值位置不完全重合。
(3)从跨段位置看,梁体拉应力敏感度由跨中向跨端呈下降趋势;从宽度方向看,梁体应力敏感度从横截面中心线处向两边逐渐下降;从高度方向看,梁体拉应力敏感度从顶板向底板呈提高趋势。因此基于第一强度理论,在今后的桥检工作中应对桥梁跨中的底板底部加以重视。

