基于改进粒子群算法的配电网多目标重构

宋紫阳, 张 菁, 刘小康, 刘传修

(上海工程技术大学 电子电气工程学院,上海201620)

0 引 言

配电网处于电网末端,是联接电网与负荷间的重要桥梁。 配电网重构是通过改变其现有网络结构中开关闭合状态,达到降低配网损耗、负载均衡及提升电压质量,使电网呈现最佳状态运行的目的［1］。

配电网重构属于典型的高维多目标非线性优化问题,国内外学者对此进行了大量的研究。 以往有关配电网重构多数以系统网络损耗最小为目标的单目标重构［2］。 此外一些研究以多个优化目标进行的重构,如：选取系统有功损耗、系统年缺供电量、系统平均停电时间及系统平均停电频率的四个指标作为重构目标函数；建立兼顾开关操作次数、电压偏移和网络损耗的多目标优化重构模型；以均衡节点电压偏移和减少有功损耗为目标,采用加权方法处理多目标优化问题,具有较多的人为主观性。

随着分布式电源(Distributed Generation, DG)接入电网的比例逐年增长,大量文献对此进行了研究,如：考虑分布式电源不确定性,利用仿射数对不确定性进行分析建模,引入列约束算法求解模型,所建立的重构方法提高了重构的鲁棒性,同时增加了计算难度；考虑多种DG 的优化重构方法,提出包含多种DG 出力的潮流计算方法,建立以DG 出力有功网络损耗最小的模型；运用二进制量子粒子群算法对配电网重构进行优化,采用遗传算法的交叉和变异克服粒子早熟问题,提高算法的收索性能。 以上算法存在以下两点不足：①直接将DG 作为负的负荷处理,缺乏实际应用性。 ②对确定模糊隶属函数的设计存在较多主观因素。

当前应用于求解配电网重构的人工智能算法,主要有蚁群算法、遗传算法、神经网络算法、粒子群算 法。 粒 子 群 优 化 算 法 ( Particle Swarm Optimization, PSO)由于原理简单、易于编程及鲁棒性强等特点,被广泛的应用到解决配电网重构问题当中。 本文建立网络损耗最小、电压偏移指数最低及负荷均衡度最优的配电网重构多目标优化模型,采用弱Pareto 支配关系的R2 指标和分解策略的混合多目标粒子群优化算法进行求解。 弱Pareto 支配原则,可以有效弥补加权法带主观性、量纲不统一的弊端。 首先,采用R2 指标隐式精英选择策略对候选重构解进行筛选,产生新的精英粒子群REP,从REP 中随机选择全局极值(Global Best, gBest)； 其次,采用PBI 分解策略对个体极值(Personal Best,pBest)进行更新,保证了算法的收敛性和多样性；最后,采用精英学习策略(Elite Learning Strategies,ELS)和高斯学习策略(Gauss Learning Strategy,GLS)协助粒子群跳出局部最优。 IEEE 33 节点算例测试结果表明：算法可以有效快速求解多目标重构。

1 多目标优化重构数学模型

1.1 目标函数

为了使电网运行指标(网络损耗、负载均衡及电压质量)呈现最佳的运行方式,建立以网络损耗最小、电压偏移指数最低、负荷均衡度最优为目标的含DG 配电网多目标优化重构。 目标函数公式(1)～公式(6)：

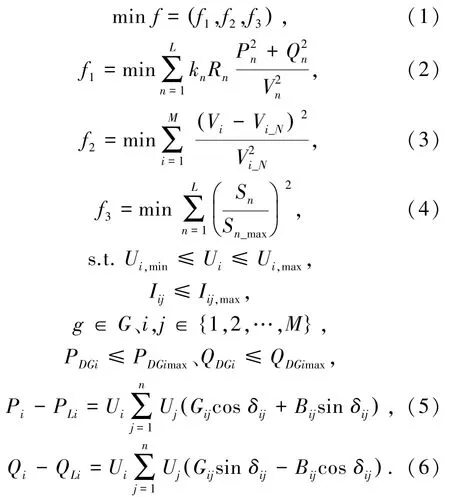
其中：L 为系统支路数,M 为系统节点数；kn为开关状态变量,1 代表开关联通,0 代表开关断开；Rn为支路n 的电阻,Pn和Qn分别代表支路n 的有功、无功功率,Vi、Vi＿n和Vn分别为节点i 的实际电压、额定电压和支路末端节点电压, Ui＿min、Ui＿max分别为节点i 最大最小电压；Iij,max为支路ij 上电流上限；Gij和Bij分别为i、j 之间的电导、电纳； Sn和Sn＿max分别为支路n 送端的复功率和最大允许传输容量； Pi、Qi、PDG、QDG、PDGi、QDGi、PDGimax、QDGimax分别为配电网流进节点i 的有功和无功功率,DG 流入节点i 的有功和无功功率,负荷在节点i 的有功和无功功率,有功和无功功率上限值； g 为重构后网络结构,G 为所有满足辐射状网络结构的集合。

1.2 分布式电源的数学模型

当前接入电网的分布式电源种类繁多,大致可分为PQ 型、PV 型和PQ(V)型三种。 因此,在计算网络潮流时需采取适应的方式进行计算。

(1)PQ 型。 异步发电风力发电机可简化成PQ节点,潮流计算中将其视为“负的负荷”处理,公式(7)：

其中： Ps和Qs分别为PQ 型DG 的有功、无功功率。

(2)PV 型。 同步发电机和含电压控制逆变器的分布式电源,输出可控的有功功率,简化处理为电压与注入功率恒定PV 节点,每次迭代过程中通过电压偏差来修正无功功率,公式(8)。

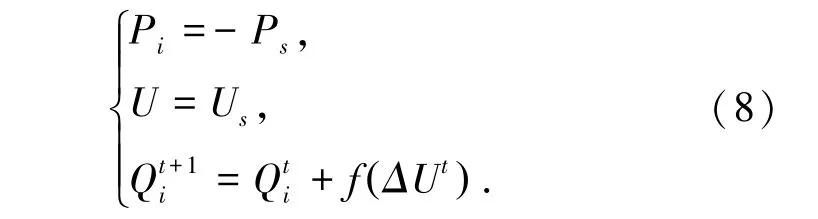
其中, t 为迭代次数； f ( ΔUt) 为无功功率修正量。

在潮流计算中为避免出现无功功率越限情况,采取公式(9)对其修正：

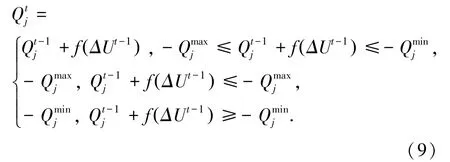
(3)PQ(V)型。 定速恒频的异步风力发电机,其本身没有励磁装置,靠电网的同步发电机为其提供励磁电流。 在潮流计算中认为输出恒定的有功功率、吸收的无功功率满足以下公式(10)关系。

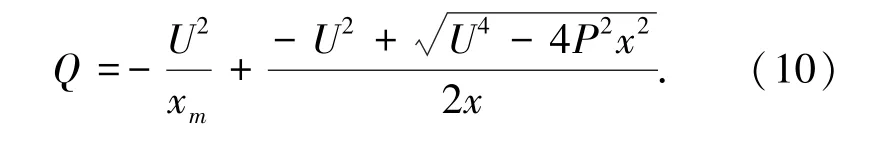
其中： xm为励磁电抗、 x 为发电机定子与转子电抗之和。

2 R2-MOPSO 优化算法

2.1 标准PSO

PSO 是一种对群体间学习机制进行模拟简化的群智能优化算法［7］。 粒子会根据gBest 和pBest 调整自己的飞行方向和速度,同时更新gBest 和pBest,向最优gBest 靠拢。

由若干个候选解构成的一个标准PSO 的初始种群。 如xi= (xi1,xi2,…,xid) 为种群内的第i 个粒子,vi= (vi1,vi2,…,vid) 为粒子速度。 式(11)为粒子的飞行速度公式、(12)为粒子位置更新公式。 为了保证粒子飞行时速度的稳定性,必须对其采取限制措施,设粒子飞行速度上限为vmax,保证粒子在合理范围内进行搜索,对飞行速度越限的粒子按照公式(13)进行修正。

2.2 R2 指标选择策略

基于Pareto 支配的多目标粒子群优化算法( Multi - objective particle swarm optimization,MOPSO)在求解多目标优化问题时,面临着算法选择压力衰减的问题,因此难以进一步的拓展到高维多目标优化问题中。 R2 指标在进行选择过程中,不仅考虑每个候选解对应权值向量的效用值,还综合考虑每个点对所有权值向量的贡献值,进而获得收敛性和多样性都较好的候选解。

采用R2 指标对候选解进行筛选。 初始化每个候选解的R2 贡献值Cx= 0,根据式(14-a)计算候选解的效用值,根据式(14-b)更新R2 贡献值,根据R2贡献值大小排序选择前N 个贡献值较大的候选解。

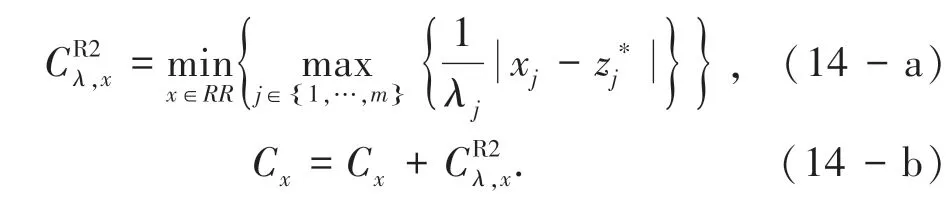
式中,RR 为筛选后重组种群, λ 为权重向量,λj≥0 且λj=1,=min {x ∈Ω},z*为参考点。

2.3 极值选择机制

极值的选择对算法的影响极为关键,采取合理的选择机制对提升算法综合性能有很大帮助。 分解策略采用可以综合权衡算法的收敛性和多样性的PBI 标量化函数(Penalty-based boundary intersection scalarizing function, PBI)如式(15)～(17)所示：

式中,λ 为权重向量,z*为参考点,θ 为设定罚函数参数且θ ＞0。

在MOPSO 算法中gBest 的选择,对算法最终的多样性和收敛性影响较大,为了权衡算法的寻优能力,算法采用从经过修剪后的N 个候选解中随机选择gBest。 然后,pBest 作为PSO 的关键,pBest 引导种群搜索至关重要,图1 给出了pBest 的更新过程。

图1 个体极值更新流程图Fig. 1 Individual extremevalue update flow chart

由于PBI 分解策略可以综合权衡算法的收敛性和多样性,因此采用PBI 分解策略对粒子的pBest进行更新,如果粒子Ta次没有更新pBest,则整个粒子群极有可能陷入局部最优解,确保整个种群的收敛性,协助算法快速跳出局部最优解,逼近真实前沿。 通过引入GLS 策略重置粒子的速度和位置,式(18)所示。

同时引入如公式(19)所示的ELS 策略协助GLS 策略求解多目标优化问题。

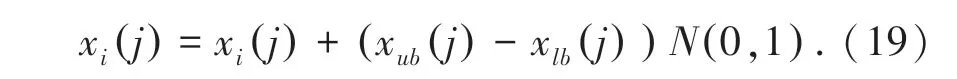
其中： xub(j ) 和xlb(j ) 分别代表第j 维决策变量空间的上下限。 N (0,1) 代表均值为0,方差为1的随机数。

3 算法流程

(1)输入网架原始数据及粒子群算法基本参数。

(2)采用二进制编码方式,随机生成一个粒子,进行连通辐射性检查,若不满足,则对其修正。

(3)根据该粒子确定的网架,进行确定性潮流计算,判断是否满足节点电压和支路潮流模糊机会约束。 若满足约束,则将保留个体。

(4)重复(2)～(3),直到生成达到初始种群规模数的初始种群。

(5)计算所有粒子的目标函数值,即为网络损耗、电压偏移指数及供电电压质量。 以此为基础,对不满足节点电压约束和潮流约束的方案,采用罚函数的方法计算粒子的适应度值。

(6)更新粒子群,粒子的pBest 为粒子本身,gBest 从生成解中随机选择。 根据式(11)更新粒子的速度,根据式(12)更新粒子的位置；根据公式(13)修正粒子越界问题。

(7)对候选解进行R2 指标选择,采用PBI 分解策略更新pBest。 若粒子Ta次没有更新pBest,采用GLS 与ELS 协助整个种群跳出局部最优。

(8)重复(5)～(7),直到最大允许迭代次数。

4 算例分析

基于IEEE 33 节点配电系统算例,采用本文所提出的基于多目标粒子群算法的配电网多目标优化重构方法进行计算。 如图2 所示,系统里存在节点33 个、支路37 条及5 个联络开关；系统的额定电压为12.66 kV,系统的有功功率为3.715 MW,无功功率为2.3 Mvar。 分别在节点7、21 和30 接入分布式电源,并设粒子种群规模为100。

图2 含DG 的IEEE 33 节点系统Fig. 2 IEEE 33 node system with DG

考虑无DG 接入网络时系统重构后的各项指标,如表1 所示。

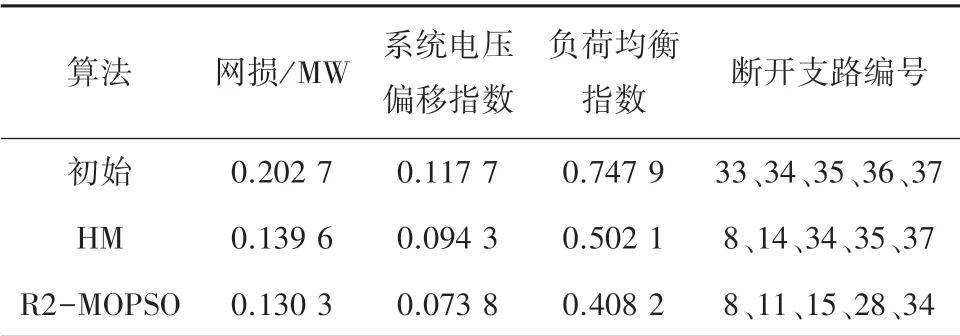
表1 未接入DG 重构网络情况Tab. 1 Network comparison without DG reconstruction

由表1 可以看出,本文所采用的R2-MOPSO 算法得到得最优重构方案网损值比初始状态降低了35.7%,电压偏移指数和负荷均衡指数均比HM 算法中的结果小。 图3 为以网损最小为目标两种算法收敛曲线图。 接入DG 多目标重构网络状态如表2 所示。

表2 接入DG 重构网络情况Tab. 2 Results of reconfiguration and optimization with DG

由表2 可以看出,本文所采用算法得到得最优重构方案的网损值比初始状态降低了40.1%,电压偏移指数改善了67.9%,负荷均衡指数改善了40.8%。各项指标均MOBPOO 的计算结果,结果表明本文所采用的算法具有良好的寻优能力。

图3 单目标重构时算法收敛曲线比较图Fig.3 Comparison of algorithm convergence curves for single target reconstruction

图4 为多目标重构三种算法对比收敛曲线图。

图4 多目标重构时算法收敛曲线比较Fig. 4 Comparison of algorithm convergence curves for multiobjective reconstruction

图5 所示,重构前后各节点电压的分布可以看出本文所采用的重构方法可以有效提升系统节点最低电压,优化网架电压分布。

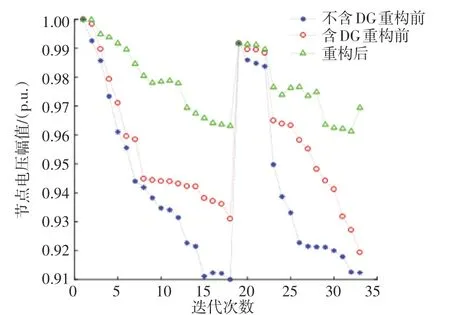
图5 IEEE 33 节点系统重构前后各节点电压Fig. 5 Voltage of nodes before and after IEEE 33 nodes system reconfiguration

将本文所采用的R2-MOPSO 算法与MOBPSO算法进行性能对比(均采取对算例进行连续50 次计算,DG 配置条件均相同),算法性能对比情况如表3 所示。

表3 算法性能对比Tab. 3 Algorithm performance comparison

由表3 可知,R2-MOPSO 算法在收敛性和寻优结果都优于MOBPSO 算法,对比结果验证了在解决配电网多目标重构问题时,本文所采用的算法具有良好的性能。

5 结束语

本文构建了以网络损耗、电压偏移、负荷均衡为目标函数及多种分布式电源的多目标优化重构模型,可以解决含有不同类型DG 的配电网多目标优化重构问题。

采用R2 指标和PBI 分解策略选择极值,精英学习策略和高斯学习策略协助跳出局部最优,可以有效地解决多目标优化时面临的难收敛、易陷入局部最优问题。 通过IEEE 33 节点算例的计算结果及对比分析表明,R2-MOPSO 能够较快的寻找到全局最优解,能够使配电网运行指标呈现最佳运行方式。本文的重构过程采用静态重构,后续将进行动态重构研究。