基于时间序列分析的长春市物流研究及预测

李明书 刘仁云 胡姝祺 闫明水

摘  要：文章为预测长春市未来的物流需求，建立ARIMA模型，对2017-2020年长春市邮政物流总量进行了分析，采用时间序列模型进行物流需求预测，用数据平稳性的判断平稳化、标准化地进行建模。利用MATLAB R2018a软件对长春市物流总量进行拟合和预测。实验结果表明：ARIMA对呈周期性变化的序列预测较为准确，对以后解决此类问题有较大的启发。

关键词：物流需求预测;ARIMA模型;Matlab

中图分类号：O211         文献标志码：A         文章编号：2095-2945（2020）32-0034-03

Abstract： In order to forecast the future logistics demand of Changchun City， this paper establishes the ARIMA model， analyzes the total amount of postal logistics in Changchun City in years 2017-2020， uses the Time Series Model to forecast the logistics demand， and models it with the judgment of data stationarity. The total amount of logistics in Changchun is fitted and predicted by Matlab R2018a software. The experimental results show that ARIMA is more accurate in predicting the sequences with periodic changes， which provides great inspiration to solve this kind of problems in the future.

Keywords： logistics demand forecasting; ARIMA Model; Matlab

物流需求預测是结合影响物流市场需求的因素，根据过去和现在的需求状况，利用一定的技术手段和预测模型，对市场的需求以及发展趋势进行预测。物流预测是进行物流管理的基础和前提，精确的物流预测可以很好地协调供应商与配送中心、仓库之间产品的分配。对物流需求进行预测有很多种方法，比如指数平滑法、移动平均法、灰色预测法、时间序列分析方法等等。在以上几种预测方法中，时间序列分析方法是预测精度较高的一种预测方法。本文借助Matlab语言软件建立了时间序列模型并进行预测，利用自相关函数，偏自相关函数的趋势筛选出比较适合长春市物流数据的模型，通过这个模型可以相对准确预测长春市未来几个月内的物流需求。

1 ARIMA模型简介

ARIMA模型（自回归积分滑动平均模型），又称为博克斯詹金森法。其基本模型包括自回归过程（AR），滑动平均过程（MA），自回归积分移动平均过程（ARMA）[5]，所谓ARIMA模型，就是将原本非平稳的时间序列通过差分等一系列方法，转化为平稳的时间序列。ARIMA模型认为依照时间顺序进行排列的所有观测值之间都具有自相关性，这种自相关性延续了变量的发展趋势。若将这种自相关性用定量的方法描述，就可以依据时间序列的过去值预测其将来值[6]。

2 建模思想

把按照时间序列排列的数据绘制成散点图，并计算数列的自相关函数、偏自相关函数，其中自相关是观察每个时点与前面时点值的相关关系，偏相关是在去除影响点后时间中的某点与前点之间的关系，并对函数进行ADF检验，观测其季节性变化规律，识别序列的平稳性。

若时间序列是非平稳的，则对序列进行平稳化处理。非平稳的时间序列一般存在着一定的上升或者下降趋势。可以对数据进行差分处理，直到处理后的数据的自相关函数值和偏自相关函数值的平均值趋于零，即时间序列趋于平稳。

依据识别规则判断时间序列模型，建立对应的模型。如果序列的自相关函数值是拖尾的，偏自相关函数值是截尾的，则该序列适合AR模型。

参数估计：AIC准则，即赤池信息准则。AIC准则同时验证了间接原则和残差不相关原则，是检验模型和确定模型参数的有力工具。

模型检验：就是判断这个模型用来描述时间序列是否合理，即模型的适应性检验。模型的适应性，是指一个时间序列模型解释系统动态性的程度[3]。因此，模型中所得到的残差序列应该是白噪声序列。若残差序列为白噪声序列，则这个模型是有效的。否则，意味着残差序列中还遗留着相关有效信息，应选择其他模型进行拟合。

对残差的白噪声检验即为模型的显著性检验。检验统计量为

如果拒绝原假设，则拟合模型不显著。如若不能拒绝原假设，则拟合模型显著有效。

模型预测：若建立的模型通过检验，则可进行预测分析。

3 应用ARIMA模型解决问题

3.1 物流预测

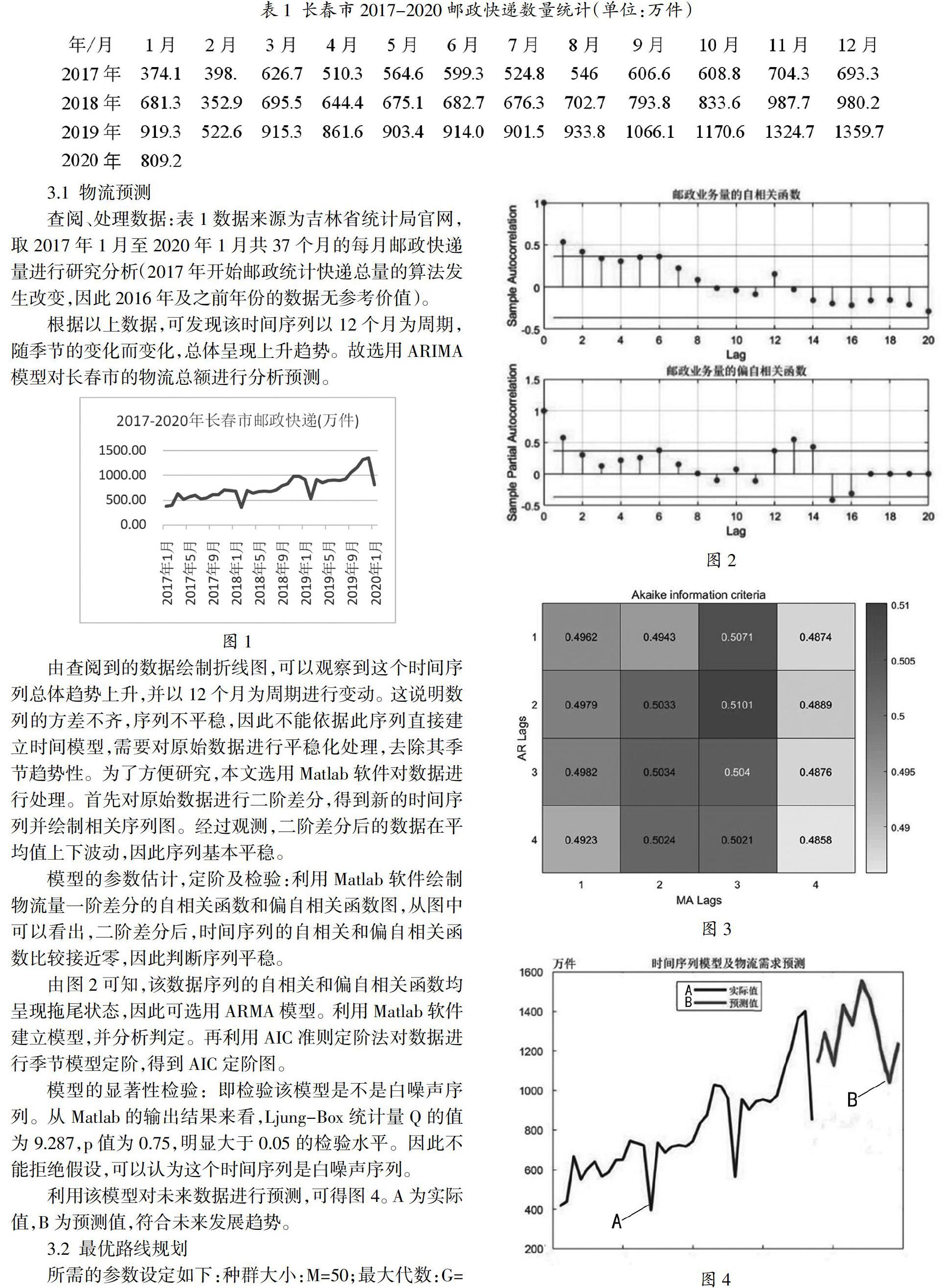
查阅、处理数据：表1数据来源为吉林省统计局官网，取2017年1月至2020年1月共37个月的每月邮政快递量进行研究分析（2017年开始邮政统计快递总量的算法发生改变，因此2016年及之前年份的数据无参考价值）。

根据以上数据，可发现该时间序列以12个月为周期，随季节的变化而变化，总体呈现上升趋势。故选用ARIMA模型对长春市的物流总额进行分析预测。

由查阅到的数据绘制折线图，可以观察到这个时间序列总体趋势上升，并以12个月为周期进行变动。这说明数列的方差不齐，序列不平稳，因此不能依据此序列直接建立时间模型，需要对原始数据进行平稳化处理，去除其季节趋势性。为了方便研究，本文选用Matlab软件对数据进行处理。首先对原始数据进行二阶差分，得到新的时间序列并绘制相关序列图。经过观测，二阶差分后的数据在平均值上下波动，因此序列基本平稳。

模型的参数估计，定阶及检验：利用Matlab软件绘制物流量一阶差分的自相关函数和偏自相关函数图，从图中可以看出，二阶差分后，时间序列的自相关和偏自相关函数比较接近零，因此判断序列平稳。

由图2可知，该数据序列的自相关和偏自相关函数均呈现拖尾状态，因此可选用ARMA模型。利用Matlab软件建立模型，并分析判定。再利用AIC准则定阶法对数据进行季节模型定阶，得到AIC定阶图。

模型的显著性检验：即检验该模型是不是白噪声序列。从Matlab的输出结果来看，Ljung-Box统计量Q的值为9.287，p值为0.75，明显大于0.05的检验水平。因此不能拒绝假设，可以认为这个时间序列是白噪声序列。

利用该模型对未来数据进行预测，可得图4。A为实际值，B为预测值，符合未来发展趋势。

3.2 最优路线规划

所需的参数设定如下：种群大小：M=50;最大代数：G=1000;交叉率：Pc=1;变异率：pm=0.1。

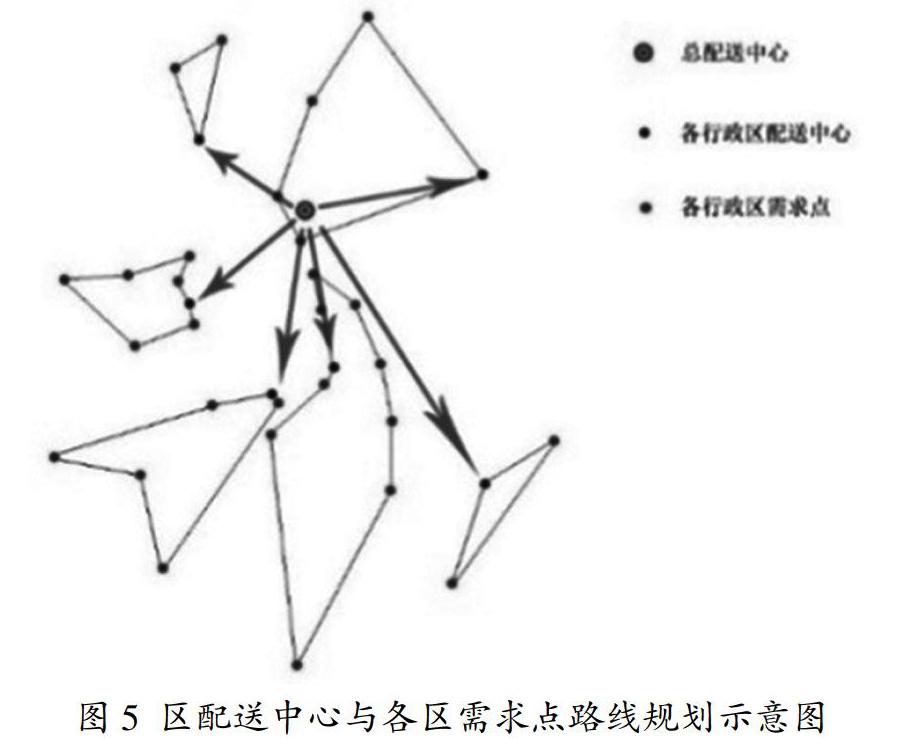
利用Matlab进行上机运算的得到的结果为127.78，运输路径如下：

经Matlab上机计算，图5的运输总路程约为127.78km，其中货车从区配送中心出发，最后回到区配送中心。最长的路线30.2km，最短的路线仅为14.38km。因此按照前文假设，货车的速度为50km/h，那么最久也只需要0.6h，所有货车便可返回区配送中心。由此看来，货物分流并增加合理的行政区配送中心点，可以缩短运货时间，使物流的运输效率更高。

4 结论

（1）长春市应根据经济结构和每个区的实际需求，合理调整物流结构。近20年来长春市发展较快，随着长春市南部净月开发区和西南部高新开发区的居民的增加，之前位于火车站旁的邮政配送中心与这两个区距离过远。配送的车辆到达这两个区的需求点难度较大。因此可以适当在长春市南部增加一个配送中心，使配送的时间和成本降低。

（2）适当增加配送车辆使库存最小化。库存是维系生产与销售的必要措施，因此买卖货品本质上只是实现了库存的转移，社会的总库存仍然不变[8]。因此库存越小，商品的流动性就越快。简而言之，如果增加了配送车辆，就会释放更多的空间，使得配送的效率大大提升。

参考文献：

[1]郑树泉.工业智能技术与应用[M].上海：上海科学技术出版社，2019：250-251.

[2]丁守銮，康家琦，王洁贞.ARIMA模型在发病率预测中的应用[J].中国医院统计，2003，10（1）：23-26.

[3]曹道友.基于改进的选择算子和交叉算子的遗传算法[J].计算机技术与发展，2010（02）：50-53+57.

[4]王燕.应用时间序列分析（第三版）[M].北京：中国人民大学出版社，2012.

[5]韦丽琴，徐勇勇，陈长生，等.ARIMA模型在交通事故预测中的应用[J].包头医学院学报，2004，20（4）：287-288.

[6]刘志学.关于供应链物流管理的一些认识[J].物流技术，2002（3）：17-21.

[7]吕树龙.ARIMA模型在降水量预测中的应用[C]//辽宁省水利学会学术年会，2013.

[8]张金艳，郭鹏江.确定性時间序列模型及ARIMA模型的应用[J].西安邮电大学学报，2009，14（3）：128-132.