基于WRF模式的强天气过程集合预报综述
董 甫,张 玲,张海鹏,李 佳,宋柳贤
(1.南京信息工程大学气象灾害预报预警与评估协同创新中心,南京信息工程大学气象灾害教育部重点实验室,江苏 南京 210044;2.南方电网科学研究院有限责任公司,广东 广州 510700)
引 言
我国地处东亚季风区,受季风影响,水汽供应丰富,常出现暴雨天气。由强降水、强对流等灾害性天气导致的气象灾害是我国最为严重的自然灾害之一。强天气过程通常包括强降水过程和强对流过程[1-2]。我国对强降水天气过程定义为:在同一个或多个天气系统相继或连续影响下,在某一区域造成的降雨强度和量值均相当大的降水天气。一般而言,24 h达到或超过50 mm的降水为暴雨。强对流天气过程定义为:出现短时强降水、雷暴、大风、冰雹、龙卷等现象的灾害性天气[3]。这些短期中尺度天气系统具有生命史短、空间尺度小、局地性强、动力机制较为复杂等特征,此类强天气的数值预报具有较大的不确定性[4]。
为了解决因初值误差、模式误差以及大气混沌特性[5-6]而引起的单一数值预报的不确定性问题,LORENZ[7]提出了集合预报思想。集合预报作为减小数值预报不确定性的有效方法,已经较为广泛应用于强天气过程的研究和预报中[8-10]。随着美国国家环境预报中心(National Centers for Environmental Prediction,NECP)于2001年建立全球第一个短期集合预报系统[11],世界上主要国家也相继建立了区域集合预报系统[12-13],实现了区域集合预报系统的业务化,大幅增强了强天气的预报能力。然而,集合预报面临的首要科学问题是如何通过恰当的扰动方法来构造合理的集合预报系统[14-15],区域中尺度数值预报中的不确定性主要来源于初值扰动、侧边界扰动、物理过程扰动以及模式扰动等,如何针对这些不确定性发展有效的集合预报扰动方法,是当前模式预报研究的热点和难点[16-17]。
随着中尺度大气模式的不断发展,WRF模式(weather research and forecasting model)因其完全开放、可移植性强、更新快等特点已得到广泛应用。本文对WRF模式在强天气过程中的集合预报进行回顾,简单介绍了WRF模式,详细论述了资料同化方法对模式初始场的改进,以及初值扰动、侧边界扰动和模式扰动等在集合预报中的研究现状,并针对对流尺度集合预报的研究现状进行总结与展望。
1 WRF模式介绍
WRF模式系统的开发计划是1997年由美国国家大气研究中心(National Center for Atmospheric Research,NCAR)中小尺度气象处、NCEP的环境模拟中心、预报系统实验室(Forecast Systems Laboratory,FSL)的预报研究处和俄克拉荷马大学的风暴分析预报中心四家单位联合发起,由美国国家自然科学基金和美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)共同支持[18]。WRF模式是一种完全可压非静力模式,采用Arakawa C网格,集数值天气预报、大气模拟及数据同化于一体的模式系统,能够很好地改善中小尺度天气的模拟和预报[19]。
WRF模式于2000年推出第一版本,此后多次改进版本[18]。2004年发布的第二版 WRF V2.0包含了单重和双重嵌套,并引入了基于三维变分的资料同化系统(three dimensional variational,3DVar)。2011年推出的WRF V3.3中,更新了四维变分的资料同化系统(four dimensional variational,4DVar)[20]。
WRF模式中的物理参数化方案主要包括云微物理参数化方案[21]、积云对流参数化方案[22]、边界层参数化方案以及陆面过程参数化方案[23]等,具体的参数化方案本文不再赘述。
2 模式初始场的改进
中尺度强对流天气常常伴随着暴雨、大风雷暴、冰雹等灾害性天气,因其局地性与短时性,现有的数值模式难以做出准确预报。要想获取准确的数值天气预报,需要具备两个条件:一是准确初值[5-7],二是准确反映大气运动规律的数值模式[24]。如何合理有效地利用中小尺度观测资料信息来改进初始场以提高中尺度数值模式预报精度,是数值模式发展的关键之一。
目前,资料同化作为一种提高初始场质量的关键手段逐渐发展起来[25]。数值预报的资料同化实质上是利用观测资料不断修正模式的预报,生成更加接近实况的模式大气状态过程,为下一时刻的预报提供更准确的初始场[26]。当前,数值模式同化的非常规观测资料主要是多普勒天气雷达观测资料,还包括卫星观测资料、自动站观测资料等[27-28]。徐广阔等[27]在常规观测资料基础上同化了多普勒天气雷达资料,发现同化多普勒天气雷达资料将有助于提高WRF模式对暴雨的模拟精度。徐枝芳等[28]在模式中同化了卫星或雷达资料,虽然两类资料引入模式后对降水预报效果不同,但都优于控制预报,对模拟结果有较大改善。因此,在模式中同化一种或多种非常规观测资料能够提高模式对降水的预报精度,说明初始场的改进对数值预报非常重要。
基于三维变分的资料同化系统(3DVar),因其简单、快速等特点,在业务上得到广泛应用,解决了非常规观测资料的同化问题[29]。3DVar通过目标函数极小化产生一个分析时刻大气真实状态的最优估计x0,其极小化函数及梯度的表达式如下:
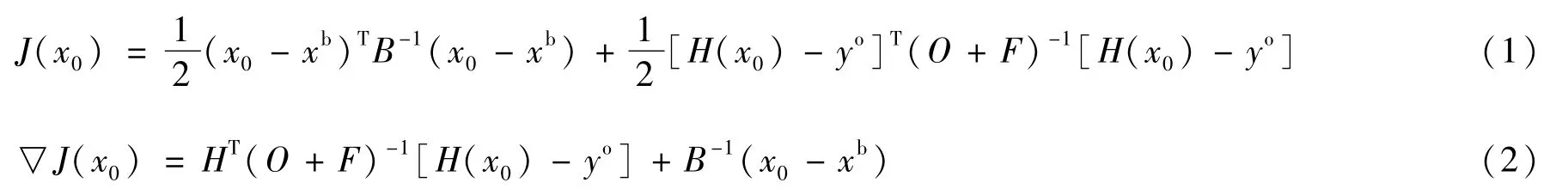
式中:x0是大气状态变量;xb为背景场;yo是观测场;H为非线性模式算子;B为背景误差协方差矩阵;O为观测误差协方差矩阵;F为预报模式协方差矩阵。
北京市气象局基于3DVar同化系统发展了北京快速更新循环同化预报系统(BJ-RUC),已经成功实现了雷达资料的实时同化,进一步提升了强天气系统的数值预报能力[30]。然而,无论是全球模式还是区域模式,4DVar同化方法较3DVar更具优势[31]。3DVar同化的观测资料仅局限在单个时刻,优化的目标是寻求瞬间的最优解。然而对一段时间而言,多个不相关的瞬间最优解,并不能构成整体上与模式一致的最优解。此外,3DVar分析结果过多依赖于预先设定的背景场误差统计模型,实际背景场误差随环流变化的特点成为其无法克服的一大难题。4DVar是3DVar在时间维的拓展,实际上是考虑一个时间窗内观测资料的分布[32],它是寻找一个最好的拟合同化时间窗内多个时刻所有观测资料的最优分析场。其目标函数为[33]:
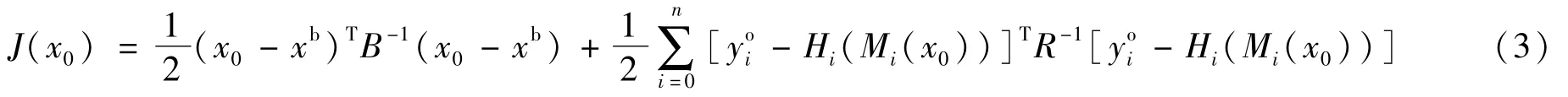
图1是2008年6月9日00:00(世界时)至10日00:00实况与不同试验下WRF模式模拟的累计降水量[34]。可以看出,雨带大致呈西南—东北向,且有3个暴雨中心,其强度自西南向东北逐渐增大;相比3DVar,4DVar具有明显优势,能够更为准确地体现A、B、C三个雨带的范围和强度。因此,如何将4DVar同化系统有效应用于中尺度高分辨率数值模式及提高4DVar同化的计算速度是目前资料同化的一个重要课题。
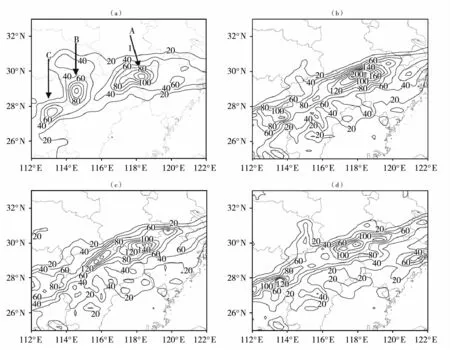
图1 2008年6月9日00:00至10日00:00实况与不同试验下WRF模式模拟的累计降水量分布[34](单位:mm)(a)实况,(b)无同化试验,(c)WRF-3DVar试验,(d)WRF-4DVar试验Fig.1 Distribution of observed and simulated accumulative precipitation under different tests of WRF model from 00:00 UTC 9 to 00:00 UTC 10 June 2008[34](Unit:mm)(a)observation,(b)control test,(c)WRF-3DVar test,(d)WRF-4DVar test
3 基于WRF模式的集合预报
由单一初始场得到的唯一模式预报结果称为确定性预报,但因大气存在混沌效应[5-7],模式无法完全捕获大气的真实状态,同时资料同化过程和模式参数化方案的不完善同样能够导致预报误差的产生,因此模式和初始场本身具有的不确定性,导致预报结果可能大相径庭。在区域中尺度模式中,初值误差、侧边界误差、物理过程误差不可避免,因此单一确定性预报具有很大的不确定性[35],而集合预报是提高强天气过程预报准确率的重要途径之一[36]。
自LEITH[37]提出集合预报理论以来,集合预报技术得到广泛发展。随着集合预报理论的不断成熟和计算能力的提高,许多国家和地区建立了相应的集合预报系统,集合预报已经成为当前解决单一预报不确定性问题的关键技术及有效手段。集合预报扰动方法是集合预报的核心问题,扰动质量的好坏直接影响到集合预报的质量[14]。模式的不确定性主要来源于初值、物理过程及侧边界等的不确定,相应地构造集合的方式应从最开始的初值扰动集合,发展到物理扰动集合、多初值多物理扰动集合、多初值多物理多边界扰动集合。针对以上中尺度区域集合预报中的不确定性,开展中尺度区域集合预报扰动方法研究是当前的热点。
3.1 初值扰动
大气是一个混沌系统,数值预报对大气的初始状态具有高度的敏感性[5-6],初始状态的不确定性会导致数值预报结果远离真实大气。因此,基于初值扰动的集合预报系统最先发展起来。
LEITH[37]于 1974年首次提出了 monte-carlo随机扰动法,是一种完全随机生成的扰动,没有任何动力学意义,致使某些扰动无法反映分析场的不确定性,故而集合预报效果较差。为了改善这一问题,HOFFMAN等[38]于 1983年提出了滞后平均法(lagged average forecasting,LAF)进行集合预报,通过在初始预报时刻前生成不同时刻的分析场,将这些分析场与初始时刻的分析场共同作为集合成员。时间滞后长度越长,则扰动的时间跨度就越大,且越临近初始时刻的扰动预报在集合预报中所占的权重越大。随后,TOTH等[39-40]提出了增长模繁殖法(breeding growth mode,BGM)来生成具有动力学意义的初始扰动,即模式中同时以分析场和扰动场进行预报,在每个培育周期结束时对扰动进行调整,并叠加到下一个培育周期的分析场上进行下一轮培育,经过一段时间的培育,得到能够反映初始场不确定性的初始扰动集合成员后进行集合预报[41]。由于能够产生具有动力学意义的初始扰动,且消耗计算资源少,BGM法得到了广泛应用[42-43],其集合预报结果明显好于确定性预报。闵锦忠等[44]在BGM法的基础上发展了滚动繁殖法和区域繁殖法,进一步提高了暴雨的预报技巧,改善了集合离散度偏低的缺陷。陈超辉等[45]考虑了对流尺度系统的局限性,发展了局地增长模培育算法(local-BGM,LBGM),其产生的离散度大于传统的BGM法 (图2)。
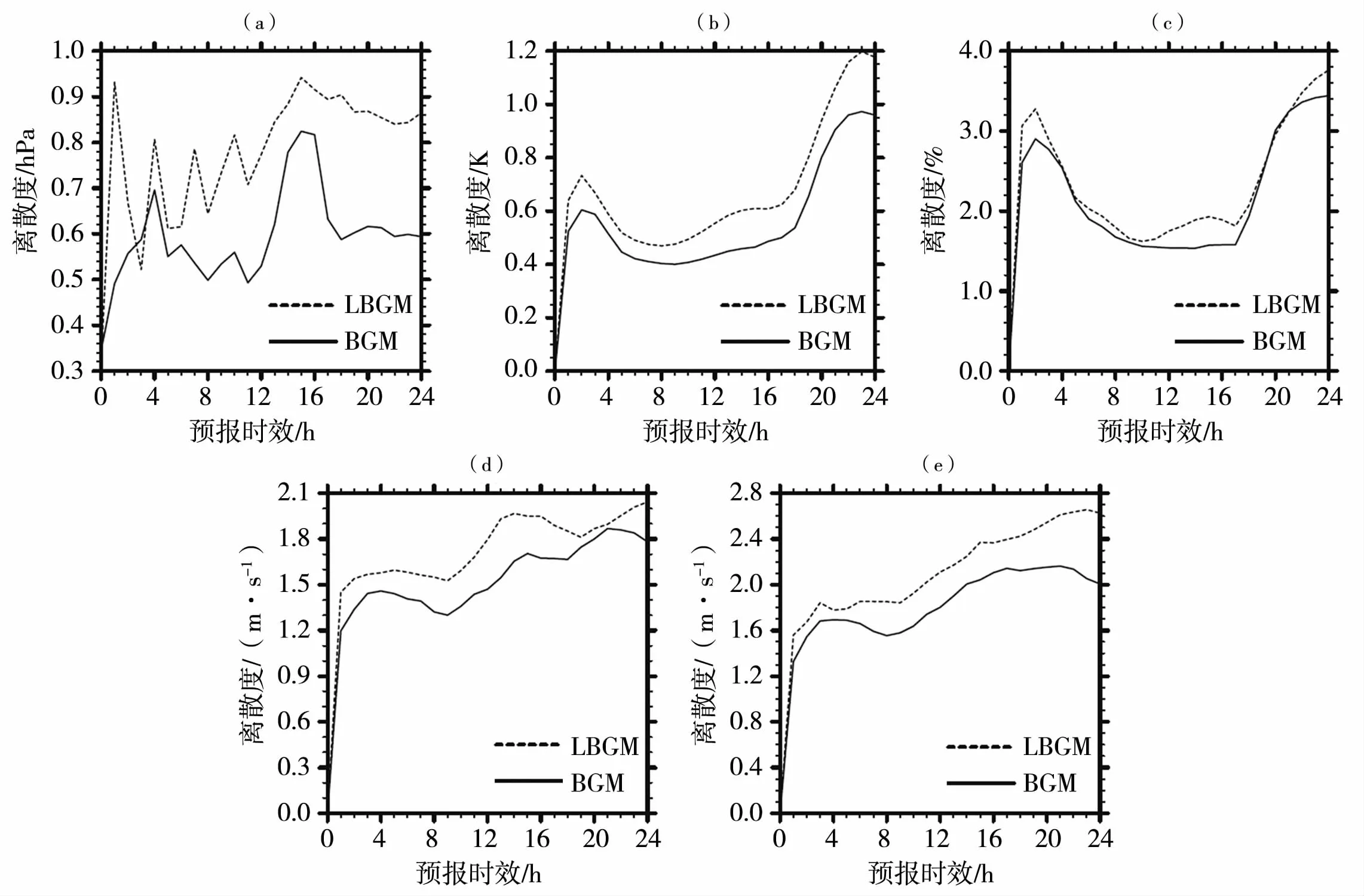
图2 近地面气象变量的离散度随预报时间演变(a)海平面气压,(b)2 m温度,(c)2 m相对湿度,(d)10 m水平纬向风速,(e)10 m水平经向风速[45]Fig.2 The evolution of dispersion of near surface meteorological variables with forecast time(a)sea surface level pressure,(b)2 m temperature,(c)2 m relative humidity,(d)10 m horizontal zonal wind speed,(e)10 m horizontal meridional wind speed[45]
2001年,BISHOP等[46]提出了基于 ET法[47]的集合变换卡尔曼滤波法(ensemble transform Kalman filter,ETKF),该方法基于集合变换思想,能够直接获得预报误差协方差的减少量,且具有卡尔曼滤波流依赖的特性,得到的集合扰动场能够反映观测场的信息,具有等概率分布和互相正交的特点。WANG等[48]最先将ETKF法应用于集合初值扰动,并同BGM法进行比较,发现ETKF法很好地弥补了BGM法的缺陷,产生的集合扰动优于BGM。WEI等[49]进一步在NCEP业务环境预报中对 ETKF与BGM进行比较,其结论与 WANG等[48]基本一致。对于一个好的初值扰动方法而言,既要能够体现中小尺度波动的不确定性,还要能够体现大尺度天气的不确定性[50],然而ETKF法包含的大尺度分量不足,不能很好地体现大尺度的不确定性,在一定程度上限制了离散度的发展[51]。目前国际上开始探索混合扰动方法[52-53],该方法可以兼顾大尺度和小尺度不确定性信息。ZHANG等[54]开展了多尺度混合扰动试验,发现大尺度混合扰动相对于ETKF方法能显著增加大尺度扰动分量,改善概率预报技巧。
研究指出,短期集合预报系统的离散度较小,且离散度和误差的关系并不理想[55],仅采用初值扰动方法不能充分反映模式大气演变的不确定性[56],仅考虑单一物理过程的初始扰动的离散度不如引入多物理过程的初始扰动方案,前者的降水评分低于后者[57](图3和图4)。为此,需要考虑侧边界、物理过程以及模式的不确定性来进一步改进集合预报系统的离散度,提高集合预报系统的预报能力。
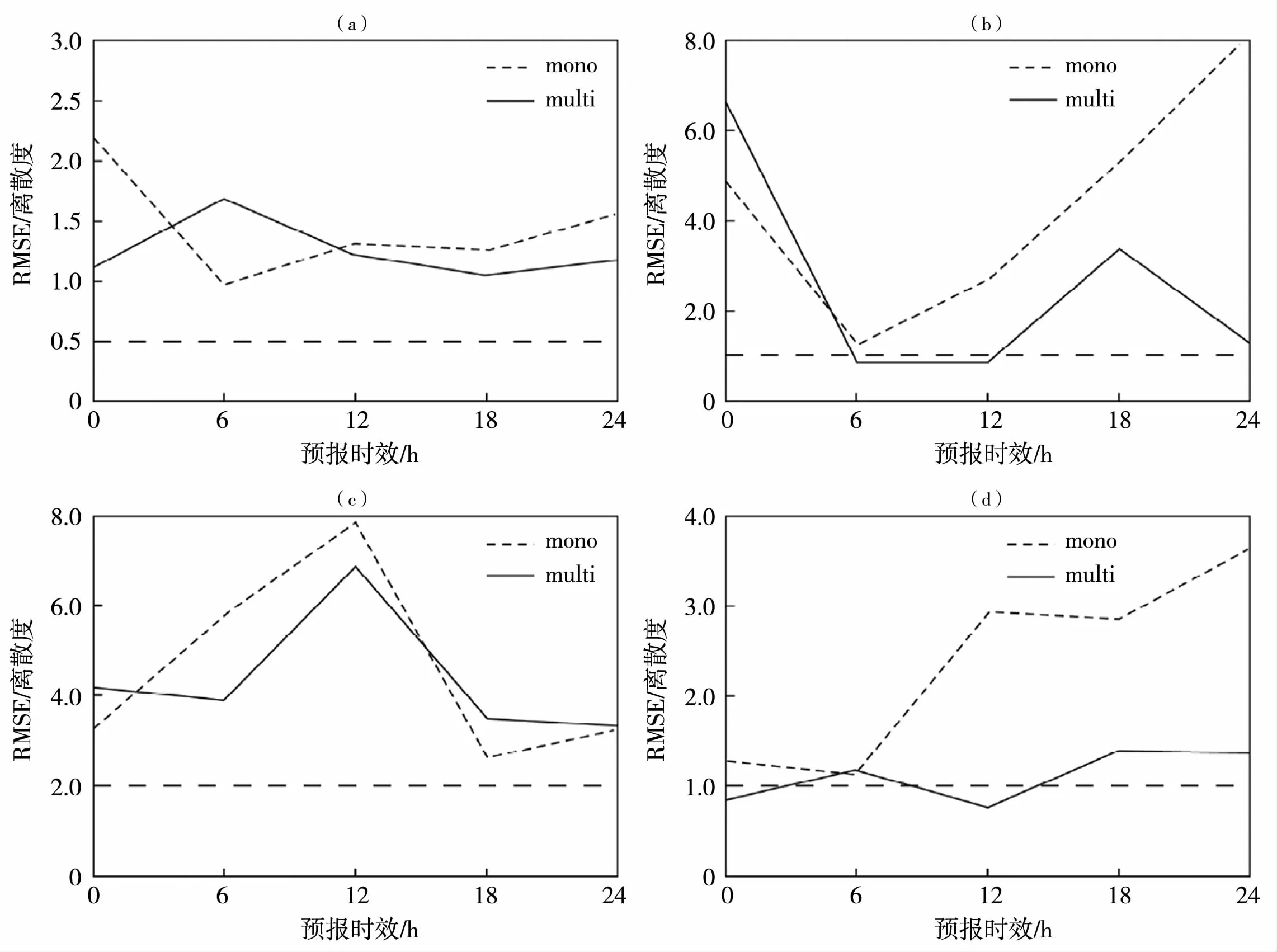
图3 强对流区域内850 hPa纬向风(a)、经向风(b)、位温(c)和水汽混合比(d)的集合均方根误差与离散度之比随时间的变化[57](mono、multi分别表示单一物理过程的ETKF试验和多物理过程的ETKF试验,下同)Fig.3 The change of ratio of ensemble mean root square error and spread of 850 hPa zonal wind(a),meridional wind(b),potential temperature(c)and water vapor mixing ratio(d)with forecast time in strong convection area[57](Mono and multi indicate single and multiple physical processes ETKF tests,respectively,the same as below)
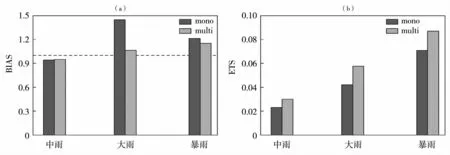
图4 单一物理过程ETKF试验和多物理过程ETKF试验下集合预报的中雨、大雨、暴雨的 BIAS(a)和 ETS(b)评分[57]Fig.4 BIAS(a)and ETS(b)score of moderate rain,heavy rain and torrential rain under single physical process ETKF test and multiple physical processes ETKF test of ensemble forecast[57]
3.2 侧边界扰动
地球上的大气在特殊地形以外不存在水平边界,而对于区域中尺度模式,因其假定大气有边界,所以不可避免地产生边界误差。HOU等[58]研究指出,在不引入侧边界扰动的情况下,单向侧边界条件严重抑制了区域集合预报的发散度。因此,区域集合预报必须充分考虑侧边界条件所引起的不确定性[59-60]。目前,大多数业务中心利用全球集合预报系统为其区域集合预报系统提供大尺度的侧边界扰动[53]。研究表明,在考虑初值扰动基础上,引入侧边界扰动能够有效提高集合预报的离散度[59,61-64],降低预报误差,且多初值、多物理过程、多侧边界方案最优[64](图5),更能代表模式大气的不确定性。
侧边界扰动与初值扰动的相互作用对模式集合预报有重要影响,但两者的相互作用机制目前还不明确,还需对其做进一步研究来发展更有效的扰动方法[62]。
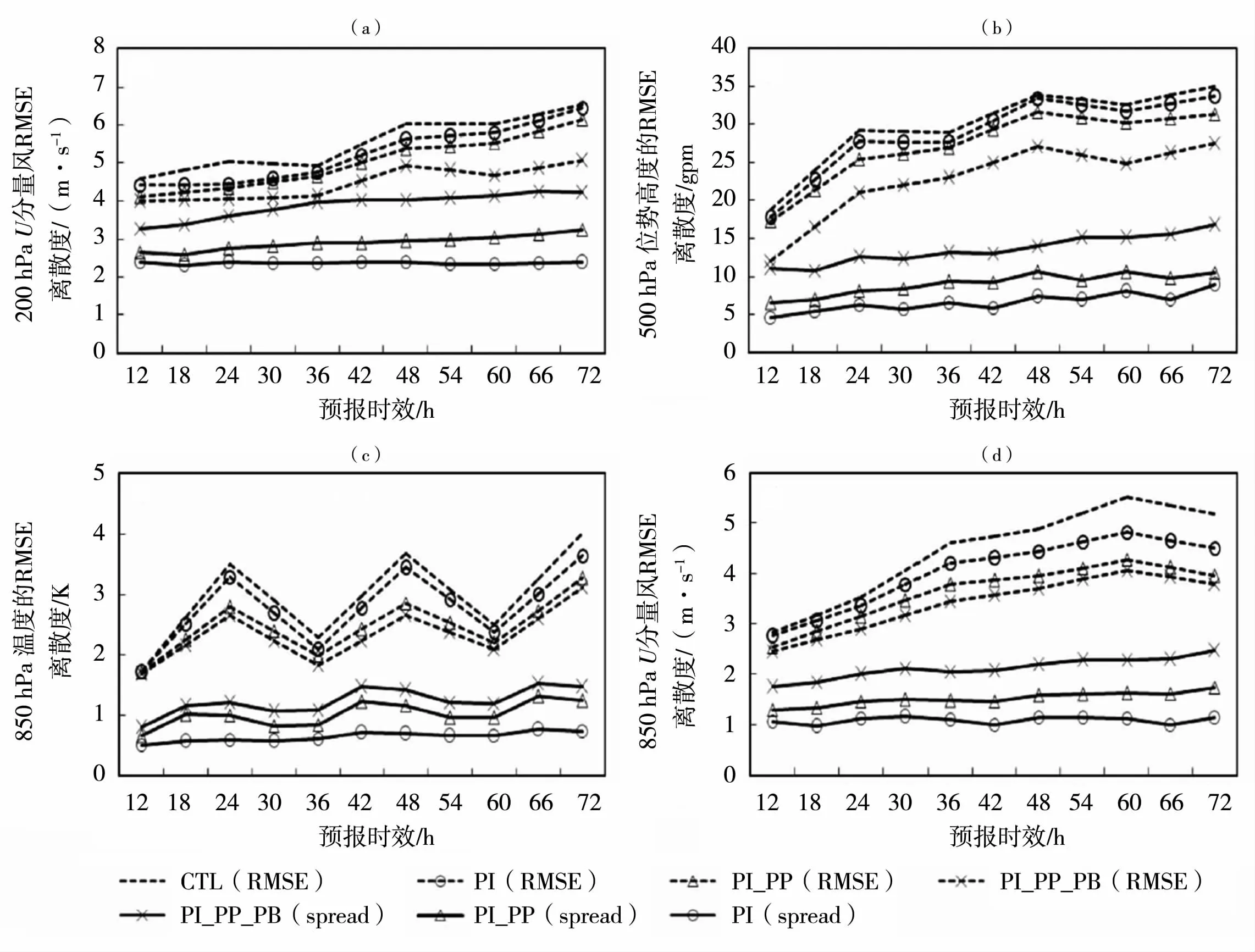
图5 控制预报和三种扰动方案集合预报的均方根误差及离散度随预报时效变化[64](a)200 hPa风场U分量,(b)500 hPa位势高度,(c)850 hPa温度,(d)850 hPa风场U分量(PI表示多初值方案,PI_PP表示多初值、多物理过程方案,PI_PP_PB表示多初值、多侧边界、多物理过程方案)Fig.5 The change of RMSE and spread for control forecast and ensemble forecast under three perturbation schemes with lead time[64](a)U component of 200 hPa wind field,(b)500 hPa geopotential height,(c)850 hPa temperature,(d)U component of 850 hPa wind field(PI,PI_PPand PI_PP_PB indicate multiple initial values scheme,multiple initial values and multiple physical processes scheme,and multiple initial values,multiple physical processes and multiple lateral boundaries scheme,respectively)
3.3 物理过程扰动
对WRF模式的参数化敏感性试验表明,物理过程参数化方案对降水模拟有十分重要的影响[20]。由于模式中物理过程同实际大气中的物理过程存在一定差距,致使模式模拟效果对物理过程方案比较敏感[65-66]。研究表明,物理过程扰动方案结合初值扰动,能够获得更好的集合离散度和概率预报技巧[67],且多物理过程的高分辨率集合预报能够较好地反映模式的不确定性[68],对均方根误差和集合离散度的改进相比于单物理过程更加明显[69]。因此,在初值扰动中加入物理过程扰动,能够显著改善集合离散度,对于提高降水预报能力具有重要意义。
基于初值扰动、侧边界扰动以及物理过程扰动的集合预报系统充分考虑了大气演变的不确定性,相比于单一确定性预报,集合预报结果更准确、稳定。然而,真实大气是十分复杂的,目前的模式预报水平和资料同化技术还不够完善,并且大多数的集合平均方法采用简单平均处理,导致集合平均预报效果与实况分析场仍有较大差距。可见,相对完善的数值模式与资料同化技术是集合预报发展的基础,而集合预报的发展与集合扰动技术的提高和预报后处理技术的发展密不可分。
4 对流尺度集合预报
强天气过程往往产生严重灾害,但因其影响范围小、过程时间短,难以预报。近年来,计算能力的提高使得数值预报模式的水平分辨率提高到1~4 km,能够较为准确地模拟出对流过程,与积云参数化方案的粗分辨率相比,高分辨率的数值模式体现出更高的预报能力[70-71]。随着灾害性天气预报精度要求的不断提高,发展对流尺度的集合预报成为目前集合预报的一项重要课题[72]。
研究发现,BGM法在对流尺度集合预报中能够较好地表示大气不确定性,集合预报结果比控制预报更为准确[73]。在此基础上针对对流尺度集合预报的强局地特征,陈超辉等[45]引入影响半径,提出了LBGM(local-BGM)法,发现LBGM法的集合离散度高于BGM,其预报均方根误差小于BGM法。另外,概率匹配平均法(probability matched mean,PMM)在对流尺度集合预报中对强降水和极端天气具有指示意义[74]。
为了能够更合理地评估高分辨率模式的预报结果,提出了空间邻域法[75],使降水预报的落区误差落在一定的邻域范围内,以保证预报结果有参考价值。研究表明,空间邻域法能够得到更多有用的对流尺度预报信息[76],且该方法在高分辨率模式的预报效果好于低分辨率模式[77]。在空间邻域的基础上,马申佳等[78]将时间因素引入,提出了一种新型邻域法,发现改进后的邻域法的高分辨率模式预报结果能够同时体现对流尺度降水事件的时、空不确定性,实现了对流尺度降水在时、空尺度上的综合评估。
目前区域集合预报模式的扰动方法在对流尺度集合预报中得到了很好的应用,并且也发展了适用于对流尺度的评估方法,但对流尺度集合预报还存在着离散度不足的问题。同时,对流尺度集合预报的强局地性特点也需要通过大量试验来确定适合不同地区的集合扰动方案。此外,由于对流系统尺度较小,对流尺度集合预报系统只能同化雷达观测资料,如何有效地同化雷达资料是提高对流尺度系统预报的重要途径之一[79]。
5 结论与展望
本文对WRF模式在集合预报中的应用进行了回顾。虽然高分辨率中尺度数值模式对强天气系统的预报有了长足进步,但资料同化技术、集合预报扰动技术以及计算条件等还处于发展阶段,强天气系统的预报还需要从以下几方面得到加强:(一)在兼顾计算资源的同时发展中尺度业务模式的4DVar同化系统;(二)发展集合预报的扰动方案,使其能够充分反映大气的不确定性;(三)提高模式分辨率,发展对流尺度集合预报系统;(四)开发适用于对流尺度集合预报的扰动方法及评估方法。
随着数值模式分辨率的提高,近年来对流尺度数值天气预报成为全球研究热点。相比于中尺度数值模式,对流尺度预报系统的分辨率更高、影响范围更小,能够更好地模拟强天气系统的发生发展过程,提高强天气过程的预报精度。然而,对流尺度系统更加复杂,对流尺度数值预报的发展需要解决更为复杂的问题,具体包括:
第一,相比较于天气尺度系统,对流尺度系统不满足准地转平衡,使得对流尺度系统在基本数学层面上难以分析,并且对流尺度系统中包含着复杂的多尺度相互作用,使得对流尺度系统的基本特征理解较为困难;
第二,对流尺度天气系统具有高度非线性的特征,发展适用于对流尺度集合预报的扰动方法及评估方法能够有效解决对流尺度集合预报非线性误差增长较快的问题,提高集合预报离散度;
第三,随着模式分辨率的提高,计算资源也相应地增多,如何平衡对流尺度集合预报的高分辨率和相应的计算资源来建立高效的集合预报系统是当前对流尺度集合预报发展的重点之一。

