基于前推回代法的含分布式电源配电网潮流计算
赵昱森
西安石油大学电子工程学院(陕西 西安 710065)
0 引言
在配电网中引入分布式电源(DG)后,配电网由单一电源转变为多种电源系统,会对配电网的网损、电压分布和电能质量产生影响。分析配电网在DG 接入后产生的影响,重要手段就是对含DG 的配电网进行潮流分析[1]。
文章在分析了各种DG 的并网特征后,介绍了DG 并网之后的简化模型,将这些DG 等效为PI、PV、PQ 与PQ(V)节点。在使用前推回代法计算潮流时,由于计算方法的缺陷,对PV 节点的计算会失效。针对此种状况,文章采用无功修正方程对节点进行无功修正[2]。
1 常见DG 在潮流计算中的模型
一般常见的含DG 的配电系统有分布式光伏发电、分布式风力发电以及燃料电池和微型燃气轮机发电等[3]。在分布式光伏发电中,在使用电流逆变器时一般将其等效为PI 节点;在使用电压逆变器时通常将其等效为PV节点。在分布式风力发电中,感应异步电机有恒速、恒频的特性,可以看作具有电压静特性的PQ(V)节点,双馈式电机一般则等效为PQ 节点。燃料电池通常在系统中等效为PV 节点;微型燃气轮机则根据对励磁控制方式的不同分为两种,当控制励磁方式为电压控制时可以看作为PV 节点;当控制方式为功率因数时等效为PQ节点[4-10]。
2 改进的前推回代法潮流计算
2.1 PV 节点的无功修正计算
对于PV 节点的处理,文章采取对PV 节点进行无功功率修正的方法,取无功功率初值为:

式中:Qmax为无功功率的上限;Qmin为无功功率的下限。
设U0为PV 节点的额定电压,则节点电压的差值△U=U0-U。可得不同迭代次数的无功功率:

式中:T 为迭代次数;△Q 为无功功率的修正值。
当配电网络的末端有n 个PV 节点时,设PV 节点处的节点阻抗矩阵为Z,有Z=R+jX ;设矩阵 ΔI˙为n 个PV节点电流变化量, 则PV 节点的电压差值可以表示为:

由复功率的公式可以得到:

配电网中节点电压的标幺值约等于1,所以可以得到:

将公式(5)代入公式(3)中,得到:
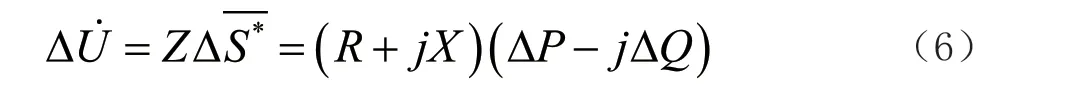
可以近似看成:

当节点类型为PV 节点时,△P=0,所以可以得到无功差值为:

2.2 PI 节点的无功修正计算
PI 节点通常为使用电流逆变器的分布式光伏发电和使用电流逆变器的微型燃气轮机。修正节点的无功功率由注入电流值、有功功率及上一次迭代电压值得出,如下:
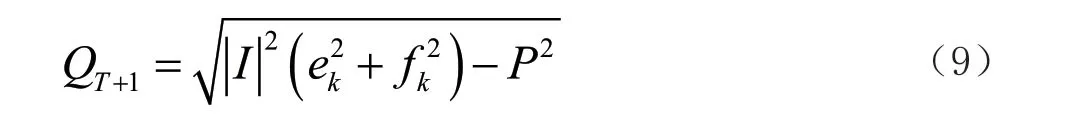
式中:P 为节点注入的有功;fk以及ek为节点电压在第k 次迭代的实部以及虚部;I 为注入电流值;QT+1为分布式电源在第k+1 次迭代的无功功率值。
2.3 PQ(V)节点的无功修正计算
感应异步电机具有恒速、恒频的特性,因此可以看作具有电压静特性的PQ(V)节点。设各个符号意义表示如下:U 为发电机端电压,kV;Is为定子电流,A;Ir为转子电流,A;Im为励磁电流,A;s 为转差率;Re为机械负载等效电阻,Ω;Xσ为漏磁抗,Ω;Xm为励磁电抗,Ω;R 为转子电阻,Ω。可以推导功率因数角正切公式以及感应电机输出电磁功率公式,分别为:
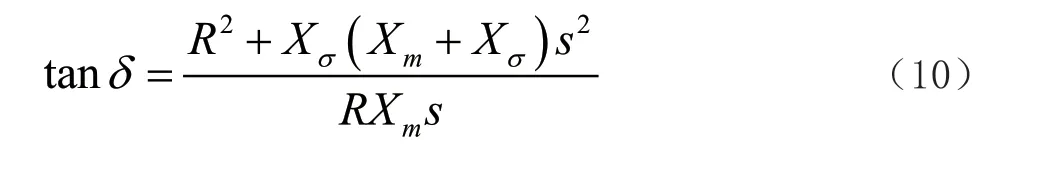

由此可以得出转差率s 公式为:

可以看出,PQ(V)节点的节点电压会影响无功功率,节点发出的有功功率是定值,则该类型节点的无功修正方程表示为:

3 改进的前推回代法的步骤
(1)输入配电网原始参数,确定配电网中DG 的位置以及节点类型。
(2)用参数计算网络等值电抗矩阵。
(3)初始化各个节点的电压初值、无功功率初值,PV 型节点的无功功率初值设为上下限的中间值,PQ(V)、PI 型节点的无功初值用上述公式计算。
(4)前推功率。从配电网络的最后开始,对每条支路,用注入功率与阻抗数据推算各支路的电流与功率损耗,推算至根节点时停止。
(5)回代电压。从根节点开始,以根节点的电压与支路功率计算各个支路的节点电压值,到线路末端停止。
(6)对PV 型节点的电压进行收敛性判断,判定条件如下:

式中:εpv为收敛精度;为该次计算得到的电压幅值;Uschi为给定的初始节点电压。若满足条件进行第7 步,若不满足则进行第8 步。
(7)判断所有非PV 节点的电压是否收敛,判断条件为该次计算得出的电压幅值上一次迭代得出的电压幅值之差,取绝对值看是否满足收敛精度。若不满足收敛精度则进入第9 步,满足条件进入最后一步。
(8)对PV 型节点的无功判断是否越界,若无功没有越界,则可以通过公式计算出无功修正功率,修正节点的无功功率。若无功越界,则将PV 节点转化为PQ 节点。转化之后,转回第4 步。
(9)用潮流计算得到的该次节点电压替换各个节点的电压初值,转回第4 步。
(10)计算结束,输出结果。
4 算例验证
为了测试上文所述的可行性,文章选取了IEEE33节点作为测试环境,如图1 所示。该配电系统共有33个节点,系统的收敛精准度ε 为10-6,系统的基准电压UB=12.66 kV,系统的基准功率SB为10 MVA。算例中所使用的四种DGS 的参数如表1 所示。

图1 IEEE33 配电系统网络拓扑结构
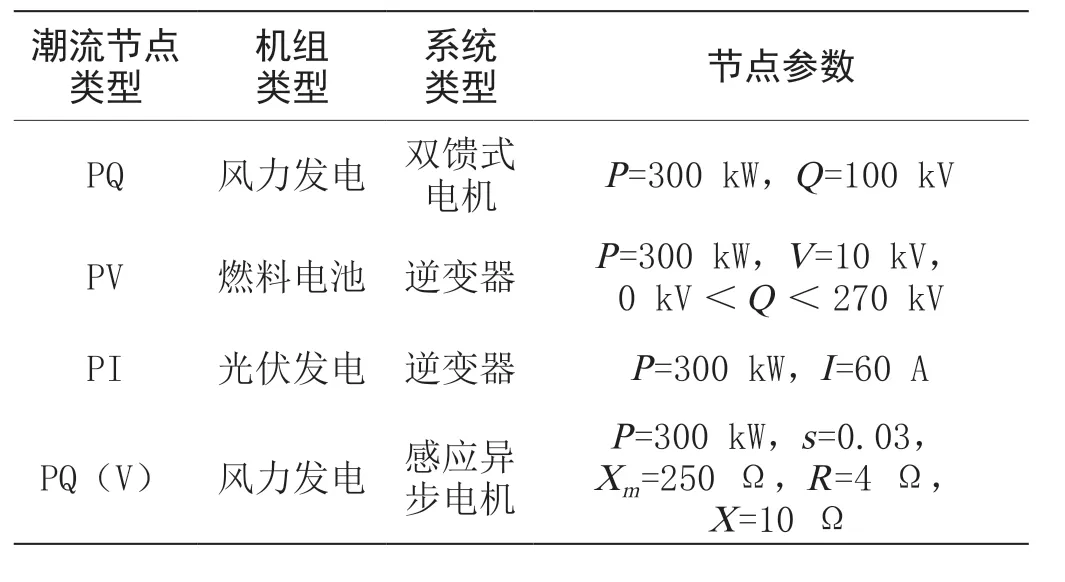
表1 四种DGS 的参数表
4.1 对算法正确性的验证
为了验证算法的正确性,实行对比实验。
实验1:在图1 的配电系统中不接入DG,线路中均为PQ 节点,除根节点外。
实验2:在节点号18、22、25、33 位置接入PQ 型DG。
实验3 ~5:接入DG 的位置与实验2 相同,接入DG类型分别为PI 型、PV 型、PQ(V)型DG。
用文章的算法分别计算以上方案,得到的电压幅值曲线如图2 所示。
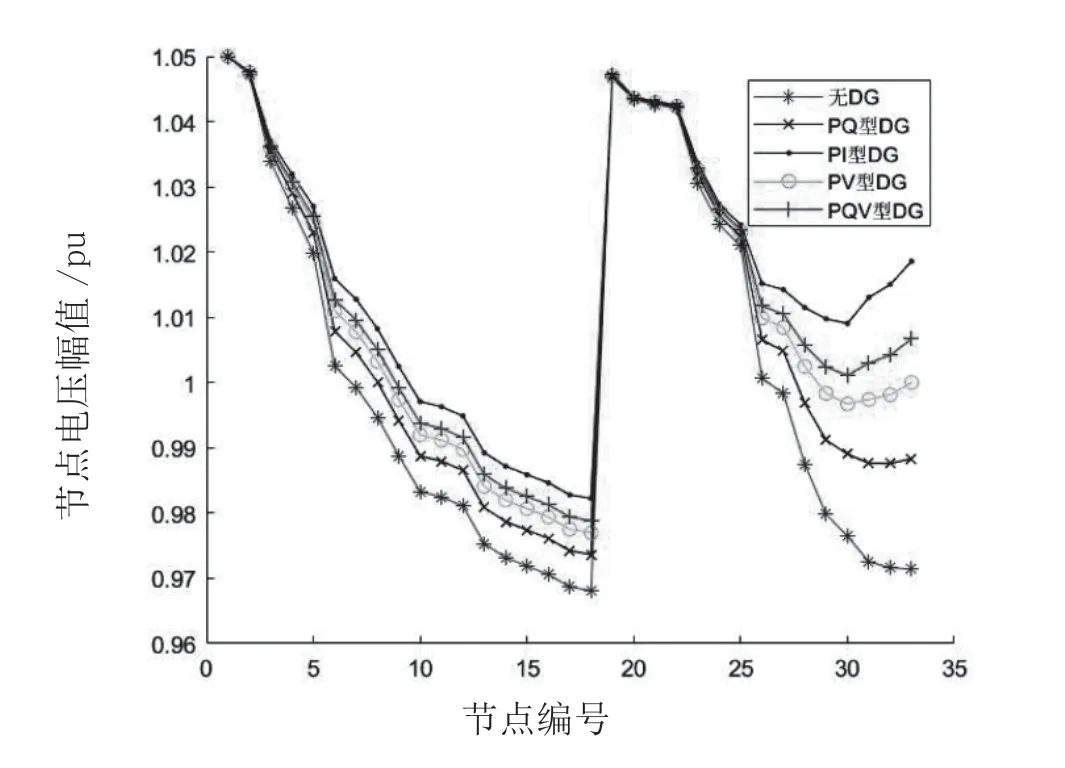
图2 五种情况的电压幅值曲线
由图2 可知,五种情况计算得到的电压幅值大体一致,证明文章算法适用于含DG 的配电系统潮流计算。
4.2 不同位置DG 对系统的影响
在同一系统中,分析DG 在不同位置时对潮流计算的影响。为了方便对比,对每种DG 类型设计了三种不同的位置情况。各种DG 接入位置以及迭代次数如表2所示。
从表2 可以看出,在潮流计算中DG 并网的位置对不同的节点类型影响也不同。对除PV 节点以外的节点而言,迭代计算的次数相差不大,几乎相同。但是对PV 型节点而言,随着PV 节点的增多,计算的迭代次数也随之增大。因为随着PV 节点的增多,需要不断地进行无功修正计算,导致潮流计算的计算量较大。
5 结论
文章使用前推回代法分析研究了配电网在含有DG的情况下的潮流计算,对常见的几种DG 进行了简要分析,并且建立了相关数学模型。在IEEE33 节点配电系统中实行了算例仿真,经过分析得知:DG 的数量以及接入配电系统的位置会影响计算速度;文章运用该方法进行无功修正,在处理PV 节点时,较容易得出结果。
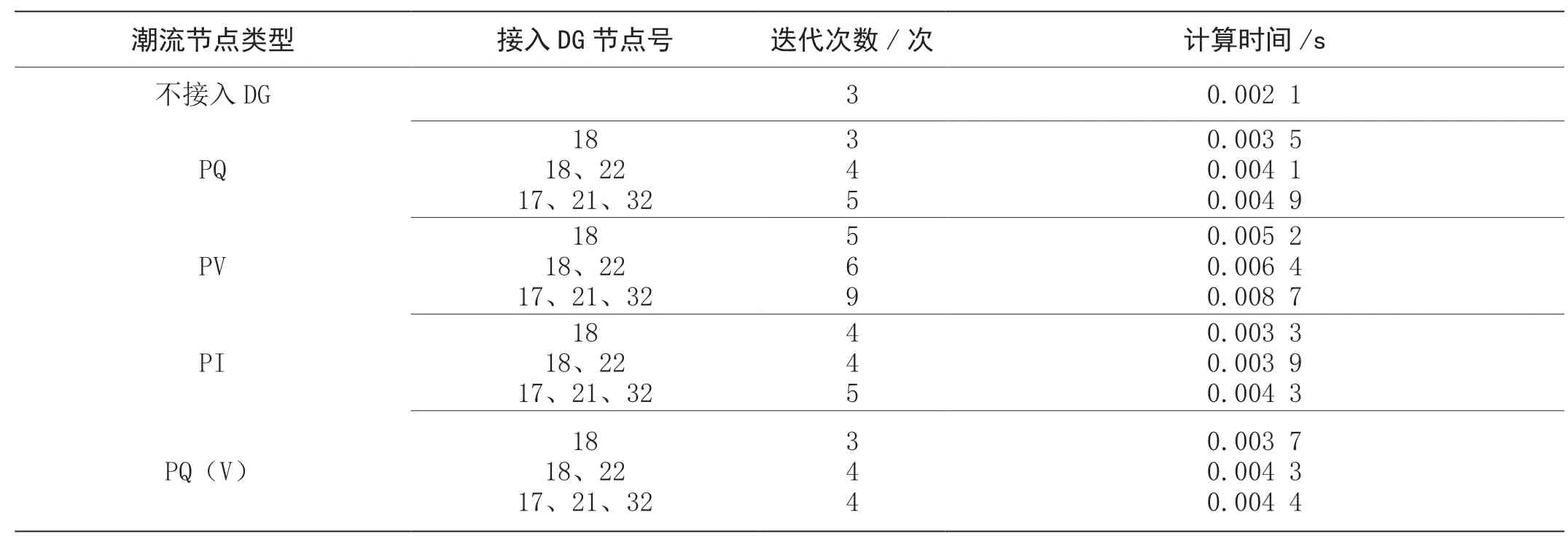
表2 各种DG 接入位置以及迭代次数

