碳酸盐岩裂缝性储层常规测井评价方法

任 杰

（中国石化中原油田分公司勘探开发研究院，郑州 450000）

0 引言

哈萨克斯坦K 油田石炭系KT-Ⅱ段储层为开阔台地相中低孔、特低渗灰岩储层。裂缝对改善碳酸盐岩油藏储层的渗流能力至关重要，裂缝不仅是重要的储集空间，而且是良好的渗流通道，还控制着溶孔、溶洞的发育与否，影响着地层中原始流体的分布状况和泥浆侵入特性，裂缝的存在对储层产能具有重要的控制作用［1-2］。电成像测井是最有力的裂缝识别手段，能够直观地显示裂缝发育的条数和裂缝的倾角［3-4］，但其测井成本较高，使得成像测井资料有限，而利用常规测井资料识别碳酸盐岩储层裂缝一直是测井技术上的难题。前人研究的利用常规测井资料评价碳酸盐岩储层裂缝的方法有很多，主要有利用双侧向电阻率高背景值下的低值及其之间的差异特征识别裂缝并评价裂缝参数的方法［5-7］、双井径曲线的差异特征识别裂缝的方法［8］、声波时差增大识别低角度缝和斜交缝的方法［9］、密度的降低或补偿中子增大指示裂缝的方法［10］等，以及一些通过数学处理手段，放大上述这些特征［11］来综合识别裂缝的方法，但这些方法由于受裂缝产状、饱和度、泥浆侵入深浅、碳酸盐岩储层次生孔隙发育［12］等多方面因素的影响，在目的层段通过取心和电成像测井与常规测井资料对比，双侧向电阻率无论在裂缝发育段，还是非裂缝层段，可能都存在正差异的特征，声波时差因受储层次生孔隙发育的影响，在低角度缝或斜交缝的储层段声波时差的增大并不明显，且裂缝发育的储层段井径、密度、补偿中子基本无变化特征，使得利用前人的方法在目的层段储层中识别裂缝及参数定量评价的过程中，存在确定性差、容易误判的缺陷。

笔者基于K 油田目的层段有限的取心和电成像测井资料对常规测井资料进行标定，在不同类型储层的测井响应特征研究基础上，利用常规测井资料对储层进行裂缝识别及参数定量评价，以期为该类油藏的合理高效开发提供依据。

1 储层测井响应特征

哈萨克斯坦K 油田取心分析和电成像测井资料综合表明，KT-Ⅱ段的储层主要有孔隙型储层和裂缝-孔隙型储层2 种类型。

1.1 孔隙型储层

K 油田KT-Ⅱ段孔隙型储层的储集空间以粒间孔为主，局部发育溶蚀性次生孔隙，裂缝的作用较小，该类型储层储集性能的好坏受孔隙和喉道的大小、分布、胶结程度以及充填物性质等多种因素的控制［13］，溶蚀性次生孔隙的存在往往对储层的渗流通道具有很好的改善作用，但也会增强储层的非均质性［14］。

在K 油田KT-Ⅱ段的电成像测井图上，孔隙型储层整体呈颜色较深的块状或团块状特征，裂缝发育特征不明显，能够观察到一定的溶蚀孔洞，一般呈不规则暗色斑点状分布在岩心照片上也能够看到溶蚀孔隙的存在。相对于非储层段，孔隙型储层常规测井曲线上表现为“两低两高”的特征（图1），即低深侧向电阻率，低密度、高声波时差、高补偿中子，且三孔隙度曲线具有较好的相关性，当储层的溶蚀孔发育时，声波时差反映的孔隙度小于补偿中子和密度反映的孔隙度。

图1 K 油田KT-Ⅱ段A 井孔隙型储层测井和岩心照片综合图Fig.1 Comprehensive logging and core photos of pore reservoir of well A of KT-Ⅱsection in K oilfield

1.2 裂缝-孔隙型储层

K 油田构造为受东西2 条逆断层控制的南北走向背斜，KT-Ⅱ段储层裂缝相对发育，裂缝-孔隙型储层是KT-Ⅱ段普遍存在的一种重要的储层类型［15］，在非储层段中，裂缝无储集、渗流的价值，而在储层段中，裂缝对储层储集空间和渗流通道都会起到积极的作用，通过与产出剖面解释成果的对比，这种类型的储层在KT-Ⅱ段很容易获得高产。

在电成像测井图上，张开裂缝表现为连续或间断的深色条带，其形状取决于裂缝的产状［16］。K 油田B 井KT-Ⅱ段中3 219～3 225 m 段在电成像测井图上裂缝发育特征显著，岩心也因储层裂缝的发育而破碎严重［图2（a）］，3 218～3 223 m 段的产出剖面解释产油量为32.5 m3/d，占全井日产量的51.4%，反映了裂缝对储层渗流改造的关键作用。相对于孔隙型储层，裂缝-孔隙型储层的常规测井响应特征表现为储层段深侧向电阻率高背景值下的低深侧向电阻率，且具有一定的弱低岩性密度，当裂缝产状为低角度缝或斜交缝时，声波时差会明显增大，但当裂缝产状为直立缝或高角度缝时，声波时差基本无反应［图2（b）］，补偿中子基本不受裂缝的影响。

图2 K 油田KT-Ⅱ段B 井裂缝-孔隙型储层测井综合图Fig.2 Comprehensive logging of fracture-pore reservoir of well B of KT-Ⅱsection in K oilfield

2 储层裂缝的识别及处理方法

上述储层测井响应特征研究表明，K 油田KT-Ⅱ段电成像和取心资料反映裂缝发育的层段，对应的深侧向电阻率、声波时差、岩性密度等常规曲线有不同程度的响应变化，而对应的自然伽马、补偿中子曲线响应基本无变化，且三孔隙度和深侧向电阻率曲线都对储层孔隙有一定的反映，因此，可利用有限的电成像和取心资料对常规测井资料进行标定，通过这些测井曲线的两两交会分析，优选出补偿中子分别与深侧向电阻率和声波时差作交会分析来识别储层段是否发育裂缝。

2.1 补偿中子和深侧向电阻率交会关系

在K 油田KT-Ⅱ段目标井段孔隙不发育的地层中深侧向电阻率多表现为大于1 500 Ω·m 的高值特征，补偿中子孔隙度稳定在零线附近，随着地层孔隙度的增大，深侧向电阻率逐渐减小，补偿中子随之增大。在非裂缝发育的层段，两者的交会关系呈较好的负相关对数关系（图3）：

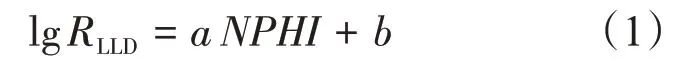
式中：RLLD为深侧向电阻率，Ω·m；NPHI为测井补偿中子值，P.U；a和b均为相关参数。

当地层中发育裂缝时，由于钻井液的侵入深度增加，导致裂缝处的深侧向电阻率明显减小，而补偿中子基本不变，依据图3 中两者的交会关系可以识别出裂缝发育段。

基于上述分析，可利用式（1）由补偿中子确定出一条基块岩石电阻率，进而在储层段中通过比较基块岩石电阻率和实测深侧向电阻率之间的大小确定出裂缝发育段，但因地层含油饱和度、沉积时期、岩性等因素的影响，深侧向电阻率和补偿中子的交会曲线是不断变化的（图4），仅利用式（1）很难准确地确定出每一个层点的基块岩石电阻率。基于此，笔者提出利用补偿中子采用最小二乘法最优化连续求取基块岩石电阻率的方法。

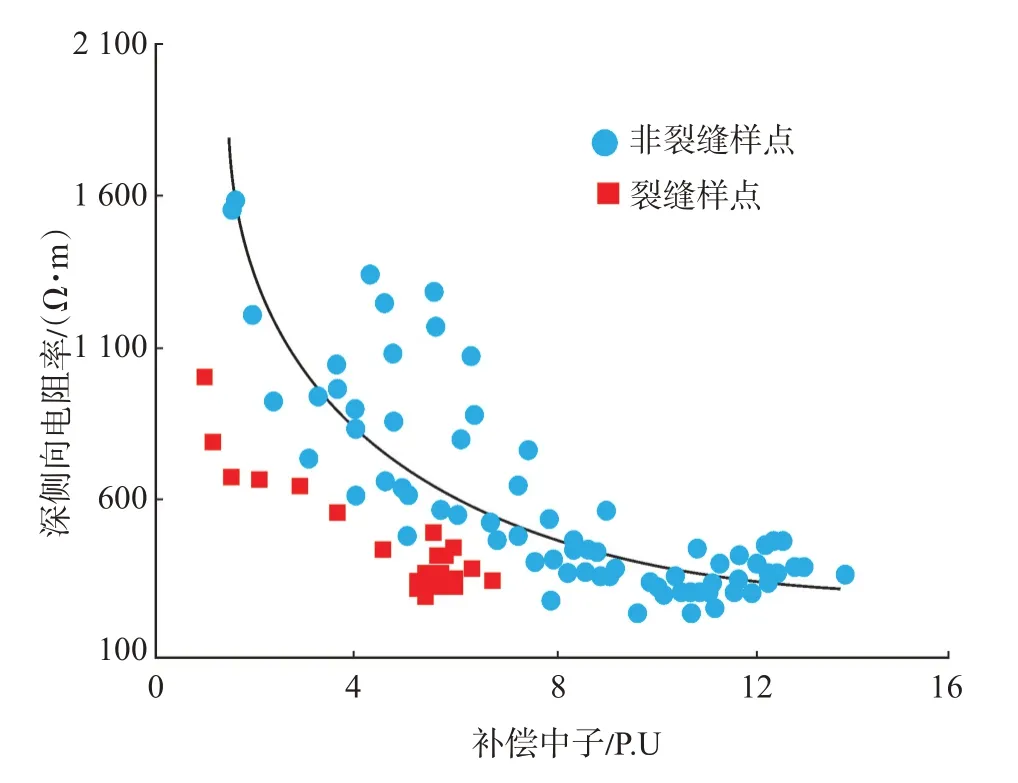
图3 K 油田KT-Ⅱ段C 井3 132～3 152 m 段深侧向电阻率和补偿中子交会图Fig.3 Crossplot of deep lateral resistivity and compensated neutron at 3 132-3 152 m of well C of KT-Ⅱsection in K oilfield

图4 K 油田KT-Ⅱ段正演的随含油饱和度变化深侧向电阻率和补偿中子交会图Fig.4 Crossplot of deep lateral resistivity and compensated neutron with the change of oil saturation in forward modeling of KT-Ⅱsection in K oilfield

选取样点计算的固定窗长m为10 m，滑动步长n为1 m，建立开窗段补偿中子和基块深侧向电阻率R基块的对数关系，其具体表达式为

利用最小二乘迭代法［17］确定出式（2）中的相关参数a和b：

式中：NPHIi为井段中第i个深度采样点对应的补偿中子值，P.U；RLLDi为井段中第i个深度采样点对应的深侧向电阻率值，Ω·m。

基于式（2）～（4）可在目标井段顶部10 m 窗长内计算出第1 个各深度采样点对应的R基块1，然后对10 m 的窗长按照1 m 的步长进行滑动（深度统一增加1 m），进入第2 个10 m 窗长内又计算出一个各深度采样点对应的R基块2，以此类推，一直计算到目标井段底部最后一个10 m 窗长为止，这样各采样点对应的基块岩石电阻率都有经过上述最小二乘迭代法确定的10 个数据，即R基块1、R基块2…R基块10，对这10 个数据进行算数平均计算，确定出该深度采样点对应的基块岩石电阻率。因最小二乘迭代法就是在不同的井段中最优化拟合的过程，上述计算方法利用最小二乘迭代法的同时，采用了算数平均方法，使得确定各深度采样点对应的基块岩石电阻率充分考虑了邻近深度采样点的测井曲线对其影响，涵盖了上述岩性、物性、含油性不断变化的地层特征，解决了利用式（1）确定基块岩石电阻率确定性差的难题。由于在实际的操作中计算量相对较大，本文的方法是利用Matlab 编程来实现的。

利用上述方法在KT-Ⅱ段内可计算出一条基块岩石电阻率曲线，将基块岩石电阻率与实测深侧向电阻率重叠。在储层段中，当基块岩石电阻率明显大于深侧向电阻率时，表明该储层段存在裂缝；当基块岩石电阻率等于或非常接近于深侧向电阻率时，表明该储层不存在裂缝。因此，可依据基块岩石电阻率与深侧向电阻率的差异来确定储层段是否发育有效裂缝，在实际应用中应排除那些因泥质或者岩性突变引起差异的井段。

2.2 补偿中子和声波时差交会关系

地层中发育低角度或斜交裂缝时，可导致声波时差增大或跳跃，但声波时差对高角度缝和直立缝的响应并不明显［18］。因此，笔者尝试利用补偿中子和声波时差的交会关系辅助上述储层段中裂缝识别的方法。在地层中随着孔隙度的增大，声波时差逐渐增大，补偿中子也随之增大，在不存在低角度缝和斜交缝的相同岩性的储层中，补偿中子NPHI和声波时差DT曲线的响应都只反映储层孔隙度的变化，两者的交会关系呈较好的正相关线性关系（图5）：

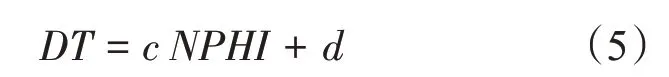
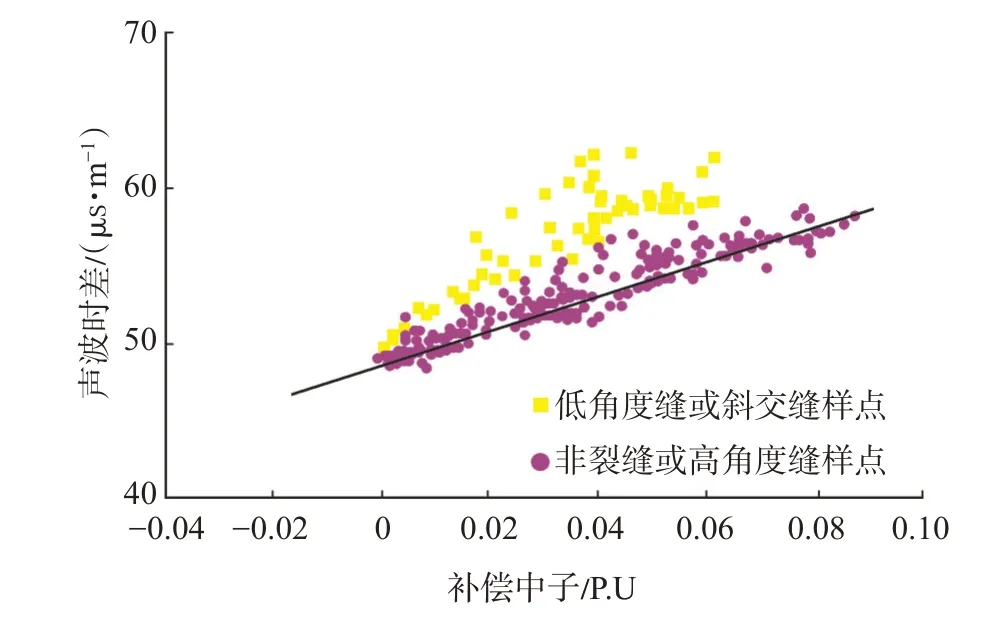
图5 K 油田KT-Ⅱ段B 井3 199～3 252 m 段补偿中子和声波时差交会图Fig.5 Crossplot of compensated neutron and acoustic time difference at 3199-3252 m of well B of KT-Ⅱsection in K oilfield

借鉴上述求取基块岩石电阻率的方法，利用补偿中子最优化连续计算确定一条基块声波时差曲线。

建立开窗段补偿中子和基块声波时差DT基块的线性关系，其具体的表现形式为

同样利用最小二乘迭代法确定出式（6）中的相关参数c和d：

式中：DTi为井段中第i个深度采样点对应的声波时差值，μs/m；c和d均为相关参数。

基于式（6）—（8），利用上述进一步确定各深度采样点对应基块岩石电阻率的方法，在目标井段内确定各深度采样点对应的基块声波时差，进而在目标井段内可计算出一条基块声波时差曲线，将基块声波时差与实测声波时差重叠，在依据基块岩石电阻率与深侧向电阻率的差异确定的裂缝段内，当基块声波时差明显小于声波时差时，则储层中存在低角度缝或斜角缝。

综合上述2 种方法，在KT-Ⅱ段的目标井段内可实现对储层的裂缝识别和判别出裂缝的产状，并对目标层段中裂缝-孔隙型储层、孔隙型储层进行划分。除此之外，基块声波时差还消除了裂缝的影响，为准确评价储层次生孔隙中溶蚀孔发育程度奠定了基础。

3 储层物性参数的解释模型

基于K 油田KT-Ⅱ段储层类型复杂多样的特点，为准确反映储层的物性特征，除计算总孔隙度外，还要确定裂缝孔隙度和基质孔隙度，进而实现对储层次生孔隙度、裂缝渗透率、总渗透率的准确计算。

3.1 裂缝孔隙度模型

目前国内外都趋向于用双侧向测井计算裂缝孔隙度［19］，但是在K 油田KT-Ⅱ段侧向测井大段存在差异，利用该方法计算结果误差较大。笔者在上节储层裂缝识别处理方法中引入的基块岩石电阻率，突出了电阻率对裂缝孔隙度的敏感性，排除了泥浆、井径、泥质及流体的影响，物理意义更加明确，可以有效地识别出储层中的裂缝，并辅助储层裂缝孔隙度的计算。

对于裂缝-孔隙型储层，裂缝被泥浆或泥浆滤液充满，基于双重介质储层的并联导电机理［20］，根据阿尔奇公式则有

式中：φf为裂缝孔隙度；φ为总孔隙度；Rw为地层水电阻率，Ω·m；Rmf为泥浆滤液电阻率，Ω·m；mb为孔隙的孔隙度指数；mf为裂缝的孔隙度指数。

通过对式（9）和式（10）联立方程求解确定储层的裂缝孔隙度：

基于式（11）可在裂缝-孔隙型储层中，计算出储层的裂缝孔隙度。

3.2 次生孔隙度模型

在碳酸盐岩储层中，通常认为补偿中子和岩性密度反映的是岩石的总孔隙度［21］，即它们反映了在其探测范围内基质孔、溶蚀孔、裂缝等的总体积，K油田KT-Ⅱ段采用经典的补偿中子和密度交会模型计算储层的总孔隙度φ：

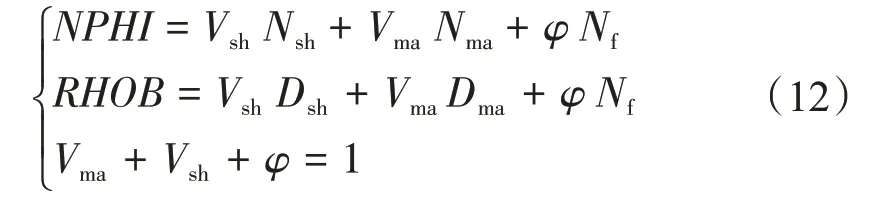
式中：Vsh为泥质体积；Vma为骨架体积；Nsh为纯泥质补偿中子，P.U；Nma为骨架岩补偿中子，P.U；Nf为孔隙流体补偿中子，P.U；RHOB为测井密度，g/cm3；Dsh为纯泥质密度，g/cm3；Dma为骨架密度，g/cm3；Df为孔隙流体密度，g/cm3。

因声波时差反映的是基质孔隙度［22］，但在K 油田KT-Ⅱ段的储层中局部可能受到低角度缝或斜交缝影响，声波时差增大，因此笔者利用上节引入的消除了裂缝影响的基块声波时差来计算基质孔隙度，采用经典的威里平均时间公式：

式中：φs为基质孔隙度；DT基块为基块声波时差，μs/m；DTma为骨架声波时差，μs/m；DTsh为纯泥质声波时差，μs/m；DTf为孔隙流体声波时差，μs/m；C p为地层压实系数。

利用上述确定的储层总孔隙度减去基质孔隙度即为储层的次生孔隙度φ2：

这里的次生孔隙度包含裂缝孔隙度和溶蚀孔孔隙度，储层溶蚀孔孔隙度φc：

式中：φ2为次生孔隙度；φc为溶蚀孔孔隙度。

3.3 裂缝渗透率模型

在碳酸盐岩储层中，前人的研究表明裂缝渗透率与裂缝孔隙度成正比，与裂缝张开度的平方成正比［23］。裂缝张开度是指在测井纵向分辨率范围内所有与井壁相切割裂缝张开度的总和。其计算方法最早是由斯伦贝谢公司西比特等人采用有限元法模拟出了不同角度、不同张开度条件下裂缝的双侧向测井响应提出的［24］，该方法提供了裂缝在不同产状下的裂缝张开度计算模型，低角度缝或斜交缝张开度的计算模型［25］为

高角度缝或直立缝张开度的计算模型为

式中：ε为裂缝张开度，mm；Rm为泥浆电阻率，Ω·m。

利用储层裂缝识别及处理方法的裂缝识别和产状判别的结果，基于式（16）和式（17）便可计算出不同裂缝产状条件下的储层裂缝张开度。

进一步利用上述确定的储层裂缝孔隙度和裂缝张开度，便可建立裂缝渗透率Kf的计算模型：

式中：Kf为裂缝渗透率，mD；参数b由取心物性分析或成像资料反演确定出来。

3.4 总渗透率模型

在K 油田KT-Ⅱ段的裂缝-孔隙型储层中，裂缝对储层总孔隙度的影响很小，但对总渗透率的影响却很大，在取心井目的层段的取心分析孔隙度和渗透率的交会图中（图6），裂缝-孔隙型储层和孔隙型储层的岩心样点能够显著区分，裂缝-孔隙型储层样点的分析渗透率因裂缝的存在可达到孔隙型储层样点的分析渗透率几倍到上百倍。利用孔隙型储层的岩心物性分析数据建立储层基岩孔隙的渗透率解释模型为

式中：K为储层基岩孔隙的渗透率，mD。

图6 K 油田KT-Ⅱ段储层取心分析孔隙度与渗透率关系Fig.6 Relationship between porosity and permeability of KT-Ⅱsection in K oilfield

上述基岩孔隙的渗透率K解释模型的相关系数R为0.800 9，反映储层基岩孔隙的渗透率与孔隙度有较好的相关性。

在孔隙型储层中，储层基岩孔隙的渗透率即为储层的总渗透率；在裂缝-孔隙型储层中，除基质孔或溶蚀孔产生的基岩孔隙的渗透率外，裂缝渗透率Kf对改善储层的渗流能力起着至关重要的作用，这时储层的总渗透率Kt应是基岩孔隙的渗透率与裂缝渗透率之和［26］，即

式中：Kt为储层的总渗透率，mD。

4 应用效果分析

利用本文提供的储层裂缝识别和处理方法以及物性参数的解释模型，对K 油田D 井KT-Ⅱ段储层进行了常规的测井综合评价分析（图7），在3 197～3 265 m 的11 个储层段内，一共划分出了9个裂缝-孔隙型储层段，其中1，2，3，4，6，7，8，10，11号油层均为裂缝-孔隙型储层，5，9 号油层均为孔隙型储层。

图7 K 油田KT-Ⅱ段D 井3 197～3 265 m 段的测井解释成果与产剖对比图Fig.7 Log interpretation results and production profile comparison at 3 197-3 265 m of well D of KT-Ⅱsection in K oilfield

通过测井解释与取心分析的孔隙度、渗透率对比分析表明，经过裂缝识别及参数计算的储层总渗透率与取心分析渗透率能够很好匹配，下面以1 号油层和5 号油层为例，分别对裂缝-孔隙型储层和孔隙型储层做进一步的对比分析。

1 号油层：测井解释的储层平均总孔隙度为6.1%，取心分析的孔隙度平均值为6.05%，利用本文提供的储层裂缝识别及处理方法研究表明，该段具有裂缝和孔隙共同发育的特征，且裂缝的角度以低角度缝或斜交缝为主，为典型的裂缝-孔隙型储层，解释的储层总孔隙度为6.1%，如果不考虑裂缝对储层渗透率的贡献，基岩孔隙的最大渗透率只有0.077 mD，这与取心分析的最大渗透率4.59 mD 相差较大，通过储层裂缝参数的计算，储层的总渗透率最大值为4.38 mD，能够真实反映储层的渗透性能，2007 年采用7 mm 油嘴的产出剖面结果证实1号油层产油量为67.7 m3/d，为全井最大产量的产出层段。

5 号油层：测井解释的储层平均孔隙度为10.4%，裂缝识别表明该储层不发育裂缝，为孔隙型储层，储层的总渗透率最大值为0.36 mD，该层的孔隙度虽然比1 号油层的孔隙度大，但储层的总渗透率远小于1 号油层。根据2007 年采用7 mm 油嘴的产出剖面结果，该油层日产油7.8 m3，比裂缝-孔隙型储层的1，2，3，4，6，7 和8 号层的日产油都少。

上述分析表明，裂缝对目的层段储层的渗流能力的贡献至关重要，本文研究所形成的裂缝识别及处理方法以及物性参数的解释模型能够满足目的层段储层评价的要求，支撑研究区油藏的合理高效开发。

5 结论

（1）利用补偿中子最优化连续拟合确定基块岩石电阻率、基块声波时差，并分别与深侧向电阻率、声波时差重叠综合识别储层裂缝以及判别裂缝产状的方法能够实现对K 油田目的层段油藏储层裂缝相对准确的识别。

（2）本文建立的储层裂缝孔隙度、裂缝张开度、裂缝渗透率、总孔隙度、次生孔隙度、总渗透率的定量解释模型，实现了利用常规测井资料对K 油田目的层段裂缝性碳酸盐岩储层的定量表征。

（3）碳酸盐岩储层裂缝常规测井评价是K 油田油藏评价中必不可少的关键环节，为油藏合理高效开发提供可靠的储层参数和解释结果。