基于SWAN模式的舟山海域波浪能资源的评估研究

于建民，纪棋严，郑欢，杨乐燕，王若琪，陈春锦

（浙江海洋大学海洋科学与技术学院，浙江舟山316022）

1 引言

伴随现代世界的快速发展与化石能源的日趋枯竭，太阳能、风能、核能、潮汐能、波浪能、海流能、温差能及盐差能等一系列可再生能源，得到了国内外的广泛关注。其中，波浪能作为海洋中分布最广、总量最大、分散程度最高的一种可再生清洁能源，从20 世纪70 年代开始就受到了国外学者的关注。伴随卫星高度计和海浪数值模式的快速发展，结合有限的调查和浮标观测资料，越来越多的波浪能资源评估工作得以开展。从全球范围来看，受西风带影响显著的海域，比如南大洋、黑潮延续体、湾流延续体和欧洲的北海海域拥有最强大、最丰富的波浪能资源[1-4]，其波浪能的年平均波功率密度可达40～50 kW/m。由于受到季风的影响，靠近欧亚大陆边缘海区的波浪能还具有显著的季节变化特征[4]。我国辽阔的海域也具有丰富的波浪能资源，但波浪能资源相对集中。方便开发利用的海域主要在舟山群岛以南[5-13]，其中又以南海海盆区域的波浪能最高，其年平均波功率密度可以达到20 kW/m。中国近海海域地处欧亚大陆东端，受到东亚季风的显著影响，因此，我国近海的波浪能也具有显著的季节性特征。

舟山作为中国海洋强国战略、长三角经济带和21 世纪海上丝绸之路的重要交叉点，对能源供应具有非常强烈的需求。舟山位于长江口南测、杭州湾外缘的东海海域，拥有众多形状各异、大小不一的岛屿。舟山周围海域水文环境特征复杂多变，同时受长江冲淡水、沿岸流、黑潮和天文潮等影响显著，又处于东亚季风影响区域，独特的地理优势使得舟山附近海域拥有包括波浪能、潮汐能、温差能、盐差能、太阳能和风能等一系列丰富的可再生能源。目前，舟山地区90% 以上的电力能源是以煤炭为燃料的火力发电能源（引自：http://www.zhoushan.gov.cn），仅有少量的风能、潮汐能和太阳能被有效地开发和利用。在舟山地区，开发波浪能不仅有利于减轻火力发电引发的环境效应、减少政府购置化石燃料支出，还能够与潮汐、风能和太阳能发电相互弥补，共同促进舟山能源产业的综合发展。根据前人的研究，在舟山外围海域30 m 深度等值线上具有3.4～3.5 kW/m 的平均波功率密度[14-15]。为了进一步揭示和评估舟山海域波浪能资源的时空分布状况和稳定程度，本文利用第三代浅海海浪数值模式（Simulating WAves Nearshore，SWAN）模拟了2007—2017 年舟山海域的海浪场，结合海表面有效波高和风场的月变化特征，对舟山海域波浪能资源的富集和稳定程度进行研究，并对波浪能相对丰富的朱家尖东南侧和东极岛东北侧两处海域的波功率密度的季节变化特征展开分析。

2 数据和方法

2.1 数据

风场是海浪成长过程中最重要的动力，本文使用欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）的逐日风场数据集ERA-Interim（网址：http://www.ecmwf.int/publications）驱动海浪模式。ERA-Interim 是一个使用四维变分技术的全球再分析数据集，从1979年开始逐月进行更新。本文选取了2007 年1 月—2017 年12 月共11 a 的风场数据，覆盖范围为0°～45°N、100°～150°E，空间分辨率为0.125°×0.125°，时间频率为6 h。本文使用的2014 系列全球海洋高精度水深数据（GEneral Bathymetric Chart of the Oceans，GEBCO，网址：https://www.gebco.net/）[16]是由国际水位组织（International Hydrogra -phic Organization，IHO）、政 府 间 海 洋 协 会（Inter -governmental Oceanographic Commission，IOC）和日本财团（The Nippon Foundation）共同资助的“海床2030”（Seabed 2030）项目开展测定，旨在为全球提供可获取的高精度海洋水深数据，空间分辨率为1/120°，空间范围为90°S～90°N、180°W～180°E。

2.2 模型配置

本文使用荷兰Delft 大学开发并维护的SWAN[17]对舟山海域的海浪场进行模拟。舟山海域是与渤海、波罗的海等半封闭海域不同的开阔性海域，不能够忽略由远海传入的海浪。舟山海域拥有众多的岛屿，使得在该海域内的波浪呈现出显著的非线性效应。因此，本文使用了空间分辨率比率为1∶10 的两层嵌套网格。大区域空间范围为110°～140°E，10°～41°N（见图1），空间分辨率为0.1°×0.1°；小区域空间范围为121.6°～123.1°E，29.5°～30.6°N。空间分辨率为0.01°×0.01°。大区域和小区域均从2007 年1 月1 日运算至2017 年12 月31日，每小时计算一次、每隔3 h 输出一次，均使用JONSWAP谱进行运算，增强因子γ = 3.3。

对于大区域而言，远海地区风大浪高、水深较大，海表面具有强烈的白冠耗散和较大的粗糙度，风拖曳系数CD应取为过饱和的形式[18]，因此模式的运行以Rogers 的ST6 项作为风输入和耗散方案[19]，并使用10 m 层风速；相比之下，近海区域风速较小，水深变化引起的波浪破碎远大于海表面由风导致的白冠耗散，因而小区域使用Komen 的线性风输入和耗散方案[20]。除此之外，本文还引入波浪的波-波相互作用、三波相互作用、底摩擦项、绕射项、反射项、涌浪耗散效应。对于舟山近海的海浪模拟，本文选取有效波高HSig、涌浪波高HSwell、平均绝对跨零周期Tm02、波向θ0作为输出参数。

2.3 方法

海浪模式从默认静止的初始状态开始，需要经历一定的启动时间才能够开始模式的平稳运行[6]。因此，本文将SWAN 输出数据中前8 d 作为模式的启动时间，从模式输出的第九天起开始分析。由于数值模式方案、参数的设定、运行环境的选择，以及其它一些人为因素有可能使运算的结果出现较大的偏差，因此需要对其进行验证，从而确保模拟结果的真实有效性。因此，本文使用了卫星海洋数据存储、验证、插值处理中心（Archiving, Validation,and Interpolation of Satellite Oceanographic，AVISO）的由多颗卫星的观测数据融合的、空间分辨率为1° × 1° 的逐 日 海表面波浪高 度（Merged Surface Wave Height，MSWH，网址：http://aviso. altimetry.fr/），将大区域的海表面有效波高（Significant Wave Height，SWH）插值到AVISO MSWH 数据的网格节点上并对其进行验证[11]，并使用式（2）和式（3）所示的U、F 方法分别检验大区域有效波高的均值和方差的有效性，计算公式如下：

式中：s1与s2表示两个样本的方差表示两个样本的均值，两个样本分别具有n1- 1 和n2- 1的自由度。

在波浪能资源评估上，绝大部分的工作都是基于海浪能量谱的概念，计算公式如下：

式中：ρ为海水密度，g为重力加速度，f和θ分别为海浪的频率和方向，E 为海浪的能量谱，cg为海浪的群速度，P 为海浪的功率密度。由于式（4）的求解太过复杂，且不能够直观地显示出波浪能量与实际海浪参数之间的关系，通常以深水波形式进行简化，计算公式如下：

式中：Hm0为波浪的有效波高，Te为波浪的周期，本文使用平均绝对跨零周期Tm02作为波浪周期。本文将依据深水波简化对舟山海域的波能进行计算和分析[6-9，11-12]，尽管对于浅水波而言可能并不能严格满足。我们将SWAN模式输出的有效波高HSig和涌浪波高HSwell进行叠加，记作海浪实际的有效波高Hm0，并将平均绝对跨零周期Tm02作为海浪的周期Te，因此，我们使用式（5）对舟山海域的波浪能进行计算。

在对舟山海域的波浪能源进行评估和开发的过程中，不仅仅需要知道波浪能的分布情况，还需要了解波浪能在时间和空间上的稳定性和持续频率[11]，最终选择能量较高、能量较稳定、高值能量持续频率较大的海域进行设备的安装和海浪能源的转化。因此，本文计算了舟山海域的海浪能在11 a间的变异系数和能级频率[3,11]，计算公式如下：

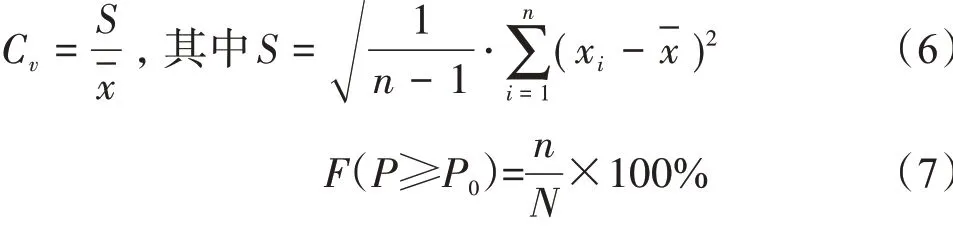
式（6）中：S 和-x 分别表示在海域内空间点上海浪能的时间序列的方差和均值；式（7）中：P0是一个常数，表示使用的特定的波功率密度大小，等号右侧表示对于某一空间点上海浪能的时间序列，当波功率密度P 高于指定波功率密度P0时的次数n 对于总次数N的占比，意为高于指定波功率密度P0时的能量频率（简称为能级频率），本文将取P0= 2kW/m。

3 结果

3.1 模式的验证

本文选取了大区域在2015—2017 年有效波高的输出数据，与AVISO 反演的有效波高进行了对比。根据均方根误差的结果（见图2a），大区域有效波高的平均均方根误差为0.4 m。由于岸线的曲折和水体成分的复杂，卫星高度计在沿岸海域有着较低的反演精度；本文未考虑环境流场对波浪的影响，因而在沿岸地区和东侧海域的位置上也具有较大的均方根误差。本文绘制了2015—2017 年大区域有效波高的模拟和反演结果散点分布图，结果显示（见图2b）：两者具有较好的一致性，但在部分格点上模拟的有效波高偏大于AVISO 的反演结果。另一方面，本文对大区域的有效波高进行了置信度α = 0.05的U检验和F检验，结果表明：东、南中国海的陆架海域基本通过了95% 的U 检验，除南海与日本海的海盆之外绝大部分海域基本通过了95% 的F检验。

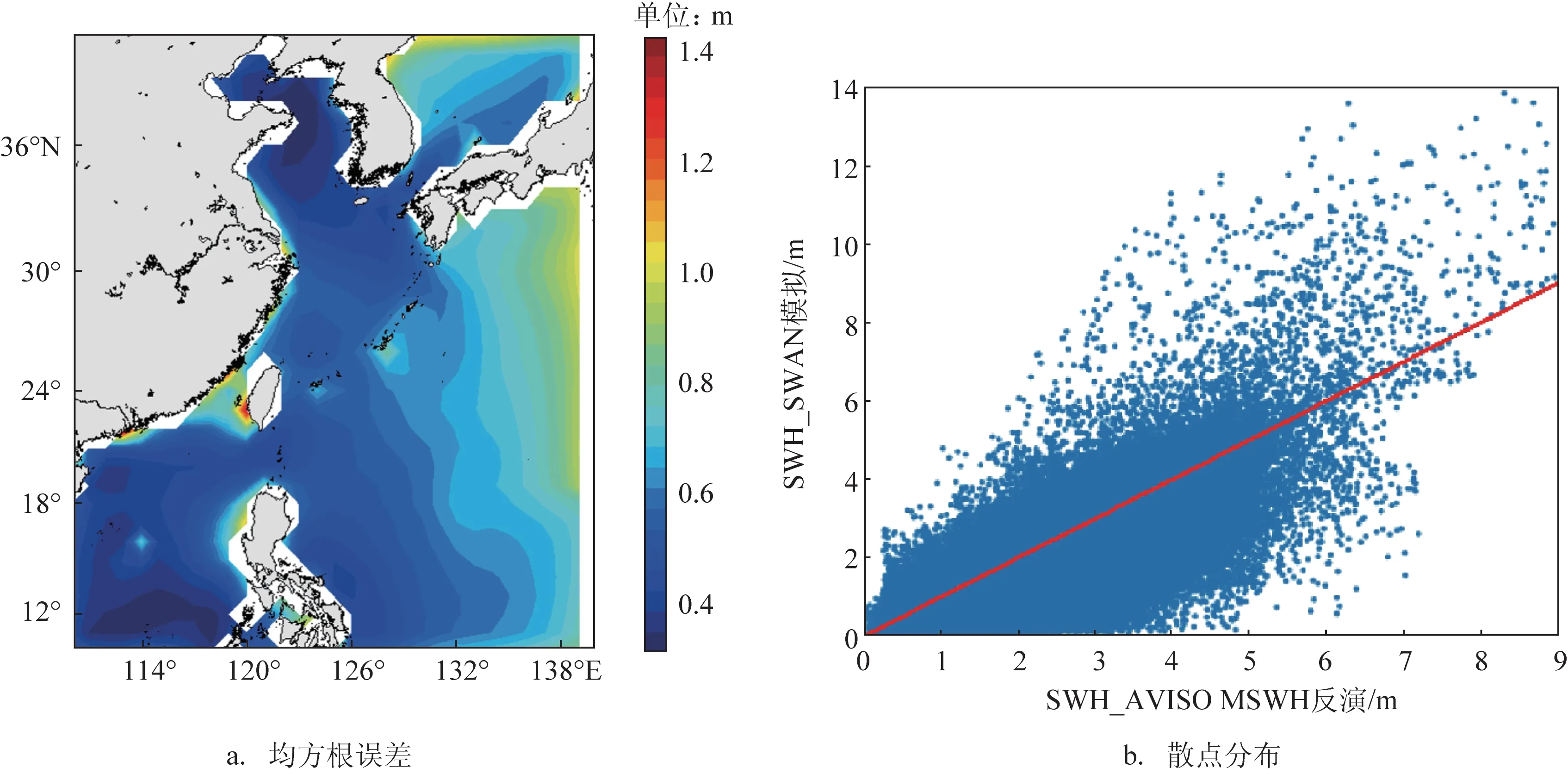
图2 2015—2017年SWAN输出的SWH与AVISO MSWH对比

3.2 有效波高的变化特征

本文将2007—2017 年SWAN 模式在小区域的11 a 有效波高做月平均处理，并叠加这个期间海面风场状况，结果如图3。冬季盛行西北季风，舟山海域与东中国海整体有着相似的变化规律[5-13]，即舟山近海的有效波高往往在冬季达到一年中的最大值。春季，中国近海处于冬-夏季风过渡期，舟山海域春季（尤其在5 月）的有效波高具有一年中的最小值。夏季盛行东南季风，由于传入的海浪未曾受到复杂岸线和水深地形的强烈耗散，因此舟山东南侧海域具有较高的量值。秋季，中国近海处于夏-冬季风过渡期，但由于大陆冷高压的影响，强台风具有较高的发生概率，风直接输入的能量较大，导致舟山海域的有效波高仍然具有较高的量值。由于岛屿的阻挡和复杂水深地形的强烈耗散，舟山海域SWH的高值区通常只会出现在东侧、东南侧以及东北侧海域。然而舟山岛南侧和宁波大陆以东海域的有效波高常年保持着舟山海域的最低值，不利于波能的开发利用。

风是海浪成长的最重要动力，风场与波浪场具有较好的一致性，利用舟山海域2007—2017年月平均的ERA-Interim 风场与有效波高的模拟结果得到风场及海浪场的玫瑰图（见图4）。其中振幅分别表示10 m 层风速和海面有效波高，而方向分别表示风向（正东为0°，正北为90°）和波向（正北为0°，正东为90°）。由图3 和图4 看出，在舟山海域，风场从冬季至夏季为北风到南风，同时伴随风向的顺时针旋转，由夏季转为冬季时又伴随着风向的逆时针旋转。舟山海域的月平均风向分布在北-东-南的方向上，最大风速来自于北-东北方向；而月平均波向分布在东-南-西的方向上，最大的有效波高伴随着射向西南方向的海浪。

3.3 波功率的变化特征

本文计算了舟山海域11 a波浪能量的月平均波功率密度，得到逐月的空间分布，结果如图5 所示。7—10 月，舟山东南方向的海域具有较大的波功率密度（其中又以7、8 月最大），1.5 kW/m 和2 kW/m 的等值线可以一直延伸到朱家尖和东极岛东南侧的海岸区域，这也是该区域全年海浪能量最大的时期。1—2 月以及12 月，1.5 kW/m 和2 kW/m 的等值线尽管可以延伸到东极岛北侧的海岸，但冬季的波浪能总量还是没有夏季丰富。与海浪有效波高的分布类似（见图3），由于季风正处于变换的过程，春季（3—5 月）的波功率密度是一年中最小的，在统计海域里波功率密度几乎没有出现过2 kW/m的密度，整体上保持着偏低的波浪能量。另外，舟山岛西北侧的杭州湾海域和舟山本岛南侧的海域，由于岛屿的阻隔和绕射效应，导致该区域成为全年波浪能最低的海域。

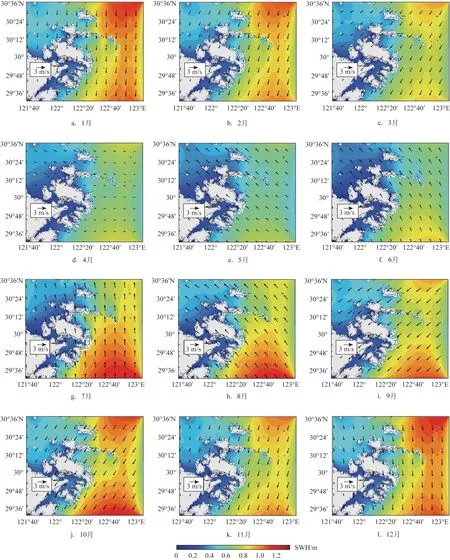
图3 有效波高的月平均分布（黑色箭头表示对应的平均风场分布）

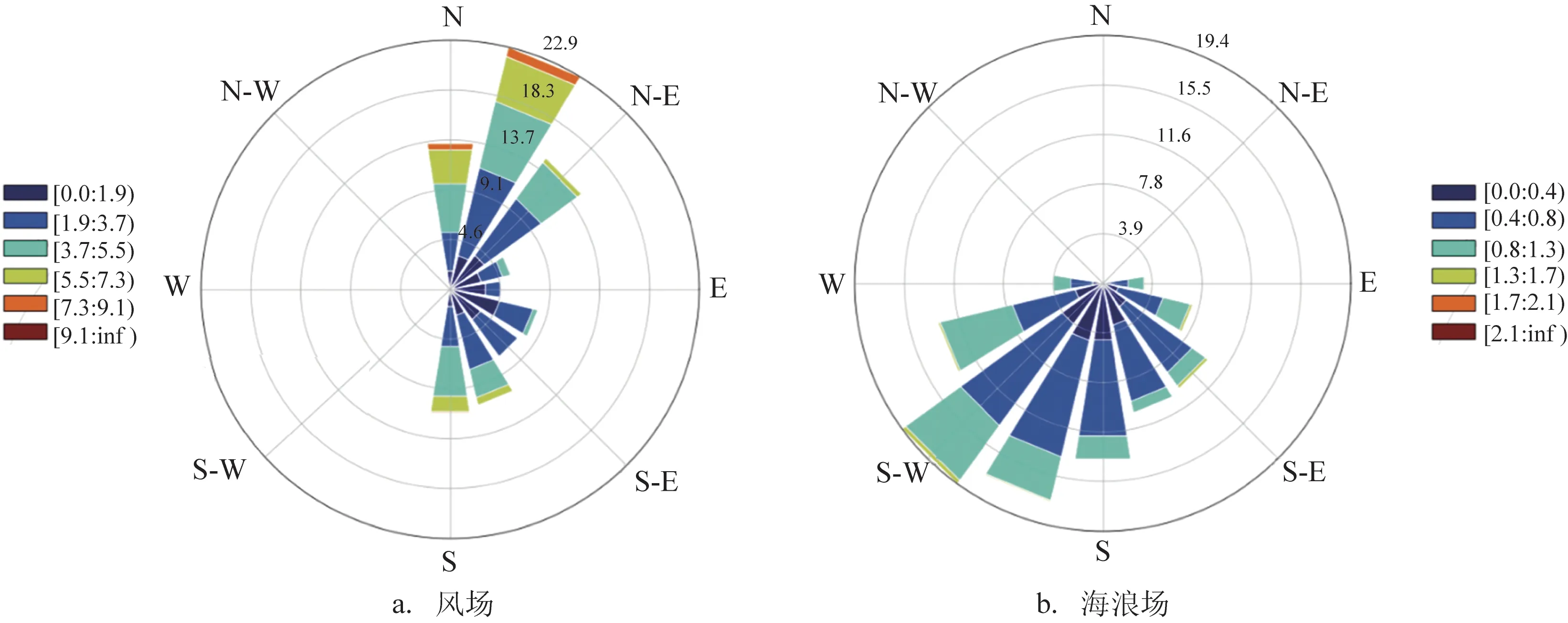
图4 舟山海域月平均的风和海浪场的玫瑰图

4 讨论

在舟山群岛以南的海域，通常是中国近海海浪能量的高值区[1]。舟山地区岛屿密布，导致在这一海域波浪具有非常强烈的非线性效应（折射、绕射等），形成了具有显著差异的波浪能分布。如图3和图5，朱家尖东南侧海域和东极岛东北侧海域具有最大的波功率密度，其年平均值分别为1.97 kW/m和1.72 kW/m，；朱家尖东南侧海域波浪能具有较高的不稳定性，在东极岛东北侧海域波浪能具有较高的可用频率。本文统计了朱家尖东南侧海域和东极岛东北侧海域在不同季节波功率密度的逐年变化趋势，如图6 和表1。其中，朱家尖东南侧海域的波浪能在冬、春季具有增大的趋势而在夏、秋季具有减小的趋势，而东极岛东北侧海域的波浪能在秋、冬季具有增大的趋势而在春、夏季具有减小的趋势。以下从能级频率和稳定性两方面对舟山海域波浪能资源进行评估。

4.1 舟山附近海域波浪能的能级频率评估

在波浪能的评估与开发过程中，能级频率是一项可以用来衡量波浪能富集程度的关键指标，是指在一定时间内波功率密度能够达到某一确定阈值的概率。国际上通常将P≥2 kW/m 和P≥20 kW/m的海域分别定义为波浪能的可用区域和富集区域[5]。本文使用P0= 2 kW/m 的波功率阈值计算在11 a 里能够满足开发利用需求的波浪能能级频率，得到其逐月的变化状况（见图7）。根据舟山海域逐月的波功率密度分布（见图5），舟山海域并不是波浪能资源的富集区，春季（尤其是5 月）是一年中波浪能最低的时期，其平均可用频率只有5%（见图7）。然而除春季之外，在朱家尖-东极岛东侧、东南侧和东北侧海域可用频率均高于20%，其中7—8 月和10 月朱家尖东南侧海域可达30%，12 月和1 月东极岛东北侧海域可达34%。另外，由于岛屿对波浪能的耗散作用，在舟山群岛西北侧的杭州湾海域和舟山岛南侧海域，可用频率始终低于5%。

4.2 舟山附近海域波浪能开发稳定性评估

波浪能的变动及其稳定性对于波浪能转换装置能否平稳运行具有重要参考意义[11]。只有在具有持续、稳定波浪能的海域，波浪能转换装置才能够正常工作。如果在某一海域波浪能具有较大的变异系数，说明这一海域的波浪能是较不稳定的；相反，如果在某一海域波浪能具有较小的变异系数，说明这一海域的波浪能是较稳定的。在波浪能较稳定的海区，转换装置才能够较容易地收集到持续且稳定的波浪能[11]，较小的变异系数对波浪能的采集和转换更加有利。因此，舟山海域波浪能的逐月变异系数如图8所示，1—5月和11—12月全部统计海域都具有非常稳定的波浪能，7 月一些岛屿或陆地（象山、岱山等）的背风侧海域具有最不稳定的波浪能。总的来说，舟山海域波浪能的稳定性在季节上同中国近海具有相似的变化规律，在冬季受冬季风的影响，波浪能的能流密度比较稳定，在夏季因频繁的台风活动和舟山海域复杂的岛屿环境，导致波浪能的稳定性较差。

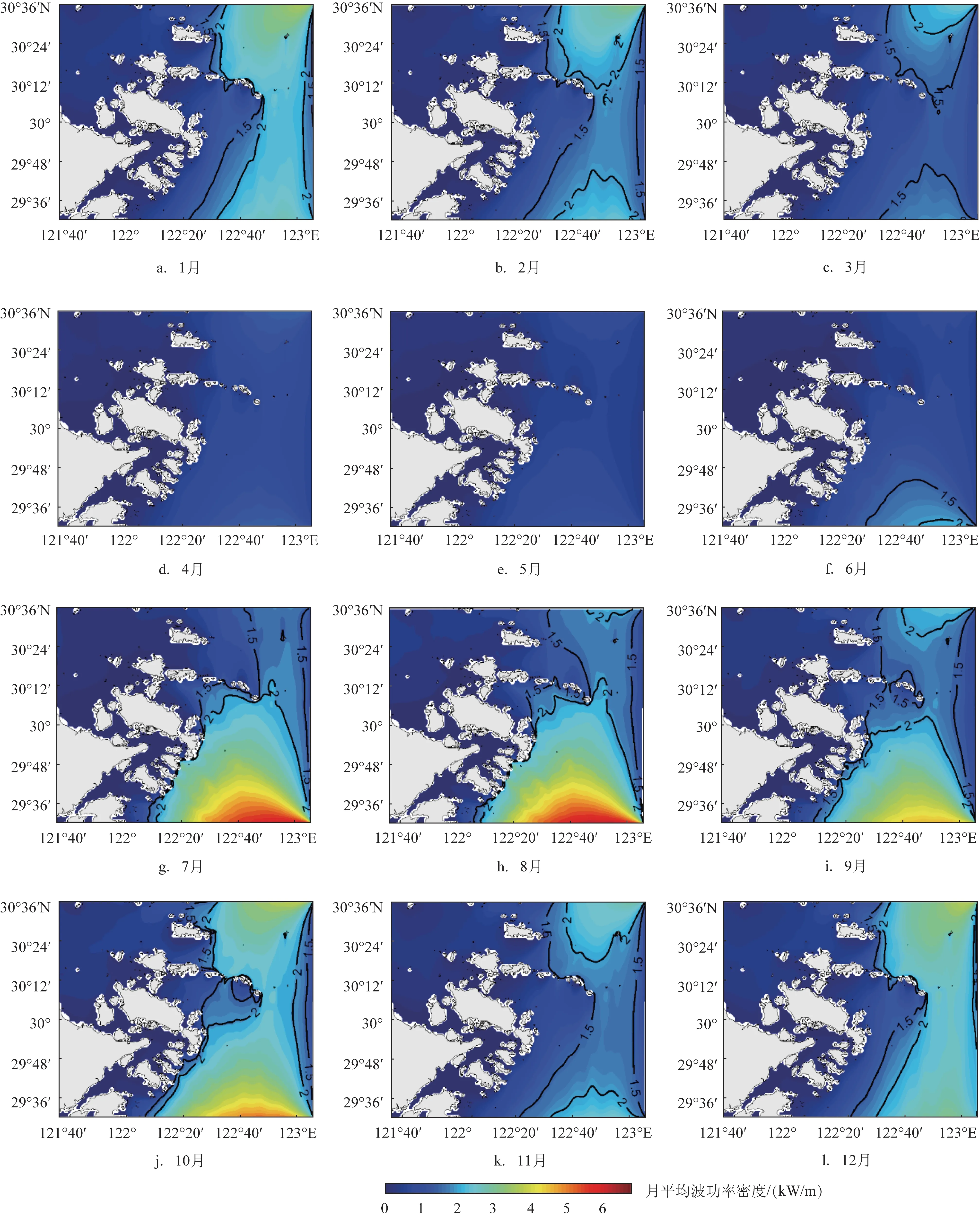
图5 波功率密度的逐月变化图

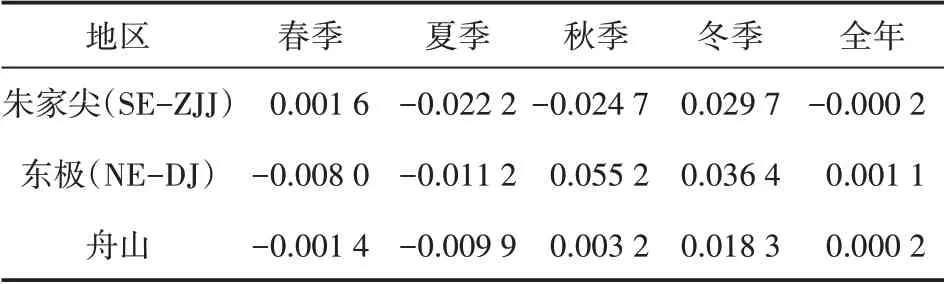
表1 在不同季节舟山海域平均波功率的逐年线性变化趋势

5 总结

本文采用海浪模式SWAN和ERA-Interim风场对2007—2017 年舟山海域的波浪场进行模拟，基于数值模拟结果对舟山附近海域波浪能资源进行了评估和分析。结果表明：舟山海域的波浪能分布具有显著的地域和季节特征。朱家尖东南方向海域的波浪能在夏季最为丰富，而东极岛东北方向海域的波浪能则在冬季最为丰富，其年平均波功率分别为1.97 kW/m 和1.73 kW/m。从能级频率角度来看，朱家尖东南侧海域在7—8 月和10 月可使用频率可达30%，东极岛东北侧海域在12月和1月可使用频率可达34%，舟山群岛西北侧的杭州湾海域和舟山岛南侧海域，可用频率始终低于5%。从波浪能稳定性角度来看，舟山海域波浪能的稳定性在季节上同中国近海具有相似的变化规律，冬季受冬季风的影响，波浪能的能流密度比较稳定；夏季因频繁的台风活动和舟山海域复杂的岛屿环境，导致波浪能的稳定性较差。东极岛东北方向海域的波浪能在富集度和稳定性方面都比周边海域好，表明该区域具有较好的波浪能开发前景。

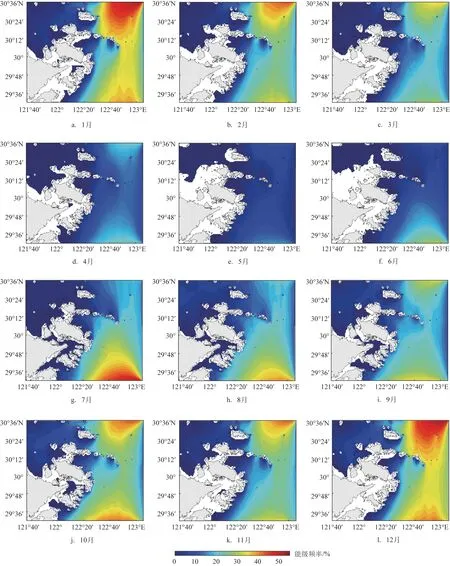
图7 在舟山海域当波浪能大于2 kW/m时逐月的能级频率（空白区域表示没有≥2 kW/m的波功率密度出现）

致谢：感谢国家超级计算天津中心THL1提供计算平台。