投资时钟框架下均值方差模型在资产配置中的应用

王 动

(中南财经政法大学 金融学院，湖北 武汉 430070)

0 引言

大类资产配置对投资有着重要的影响，但是相关理论的发展相对滞后于对单一投资品种的研究。就我国的相关研究而言，张雪莹(2005)和葛红玲(2008)分别就战略资产配置对我国基金收益的影响进行了定量分析，之后的研究主要是对一些国外的大类资产配置策略进行了引进和实证，直到2017年，张学勇、张琳对大类资产配置策略进行全面总结和归纳，提供了一个整体性的大类资产配置理论框架。臧金娟、黄一黎、赵学军(2017)对我国大类资产配置中各类资产最优代表的选择进行了研究。

张学勇、张琳(2017)将大类资产配置策略分为三大类：恒定混合策略、量化配置策略和融入经济周期和主观判断的配置策略。在20世纪60年代之前，投资者多使用恒定混合策略进行资产配置。这种策略当中最常见的是等权重策略。等权重策略是一种被动型策略，要求各大类资产市值在总资产市值当中的权重保持相等，当某类资产在总资产当中的市值占比上升一段时间后卖出，反之则买入。瑞士经济学家和基金管理人Marc Faber(2015)认为这本质上是一种反转策略，他的研究和投资实践表明，如果投资期限足够长，多样化配置的权重大类资产投资组合的表现优于多数其他策略。

量化资产配置研究肇始于Markowitz(1952)提出的均值方差模型，该模型用期望收益率来表示收益，用期望收益率分布的方差来表示风险，投资目标既考虑了投资收益，又考虑了投资风险，把资产配置问题转化为多目标优化问题，为资产组合以及大类资产配置的量化分析提供了理论基础。从20世纪50年代均值方差模型的出现到90年代之前，大类资产配置处于理论探索阶段，对均值方差模型的现实应用进行不断完善。20世纪90年代以来，随着计算机技术的发展和信息的积累，使得大量金融市场数据能够应用于投资决策，出现了大量的量化型大类资产配置策略。包括以均值方差模型为基础的基于收益和风险的大类资产配置策略、仅基于收益的策略、仅基于风险的策略、基于投资者效用的策略这些类别[1]。

量化投资是从历史数据中提取信息进行资产配置的，一方面，大量量化方法的使用使得市场生态发生了变化；另一方面，宏观经济环境和经济政策会出现前所未有的变化，这些都导致了量化策略并不总是可行和有效的。机构投资者开始越来越多的考虑宏观经济走势和经济政策的变化，经验和主观判断开始越来越多地融入到大类资产配置决策当中，产生了一些融入经济周期和主观判断的大类资产配置策略，这其中最著名的是美林证券公司于2004年提出的投资时钟模型。

1 投资时钟框架下的均值方差模型

国内对投资时钟的研究主要是论证美林投资时钟策略在我国的有效性和其中经济周期阶段划分的优化问题，但是对具体配置比例进行量化研究的较少。轮动策略被认为是美林投资时钟理论相对应的大类资产配置策略，在每一经济阶段选取投资时钟理论认为的收益最高的大类资产进行配置。这种策略是以投资收益最大化为单一目标的，没有考虑通过分散化投资来降低风险。

均值方差模型作为基于收益和风险的资产配置策略为人们所熟知，但是均值方差模型本身属于静态模型，在单期投资中，事后应用已有的资产收益率数据通过二次规划方法可以求出投资的有效边界。但是如果动态地应用于资产配置决策当中，则需要估计投资期内的资产预期收益和各类资产之间的相关系数和协方差矩阵，这一过程繁杂而且容易出现偏差。同时，该模型对预测数据的微小偏差又过于敏感，微小的偏差就会较大程度地影响资产配置权重的确定，导致实际资产配置组合偏离事后实际数据计算的有效边界。因此，经典的均值方差模型被认为只是适合作为理论参考，并不适合直接应用于大类资产配置决策。韩其恒、吴文生、曹志广(2016年)运用六组中国资本市场数据对经典的均值方差模型按照不同期限长度的估计窗口进行了回测，发现通过估计窗口的变化并不能有效改善估计误差。他们还对均值方差模型进行了贝叶斯法、收缩法等方法的改进，改进后的模型表现也不尽人意，甚至逊色于简单的等权重模型[2]。

均值方差模型:

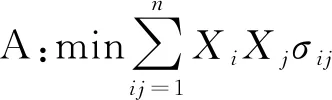
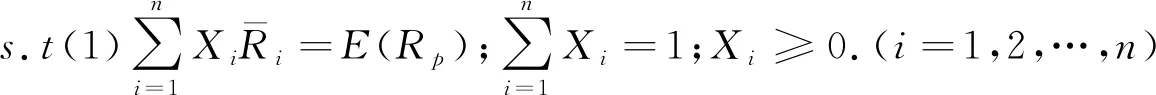
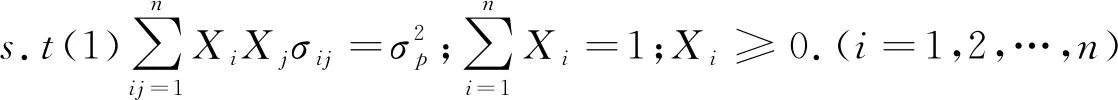
模型A代表期望收益水平确定下的最小风险有效集；模型B代表风险水平确定下的最大期望收益有效集。

本文尝试在投资时钟框架下解决均值方差模型的动态化问题。因为投资时钟的有效性，所以假定前一周期各阶段的收益率均值和协方差矩阵可以作为下一周期相同阶段的预测值应用于均值方差模型，这样均值方差模型就可以运用于大类资产配置比例的确定。本文将首先对我国的经济阶段在较长周期上进行划分，然后把前一周期的相关数据作为预期值运用于均值方差模型，对下一周期的大类资产配置进行回测实证，然后把该策略绩效与资产轮动策略等常见策略的绩效进行对比来检验这种策略的有效性。

2 投资周期的划分

2.1 美林投资时钟

美林投资时钟是美林证券于2004年在一份投资报告中提出的，是一种将大类资产表现和经济周期的不同阶段联系起来的一种资产配置方法。它首先基于美国近30年的经济数据，以产出缺口和CPI同比增长率刻画经济增长和通货膨胀，从这两个维度把经济周期划分为复苏、过热、滞涨、衰退四个阶段，对不同阶段大类资产的表现进行了分析与实证，认为这四个阶段各类资产的收益排序具有相对稳定性，会伴随经济周期产生周而复始的轮动表现，大类资产的投资也应该进行相应的配置。具体结论见表1。

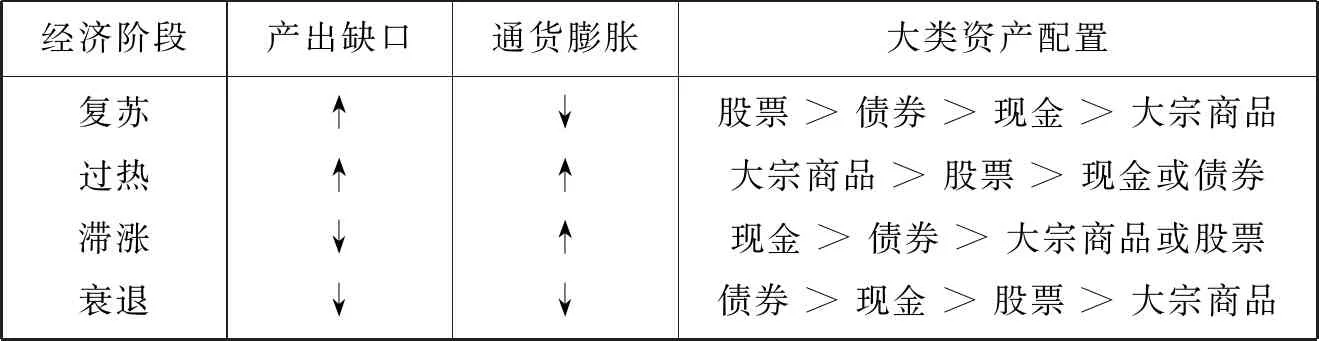
表1 美林投资时钟与大类资产配置

2.2 周期判断指标和拐点判断方法

投资时钟理论应用的关键是经济周期阶段的划分是否能够反映本国经济波动的真实趋势。有关经济周期的理论和判断指标众多，美林证券报告中采用了央行政策指标、NBER先行指标、商业信心指数、GDP预期指数、通胀指标、经合组织产出缺口、原油价格、CPI预期指数等指标来判断未来六个月的经济周期阶段[3]。这些指标有的在我国难以获取，有的不适合我国的经济现实，于是国内的投资研究机构采用了一些简化的指标体系。[4-6]具体指标见表2。

在对数据处理、周期拐点判断方面，各家研究机构也采用了不同的方法、模型和规则。

本文在指标选择方面的原则是减少数据处理环节和避免估计误差，采用了中金公司的指标体系：工业增加值同比增长率(IVA)和CPI。因为在随后的实证检验中使用的投资收益率是月收益率，故采用原始月度数据的IVA而不是季度数据的GDP。产出缺口是实际产出和产出的潜在水平之间的差值，其中产出的潜在水平是一个需要估计的值，相比产出缺口，使用IVA避免了对数据进行估计产生的误差。[7-8]数据处理方面，采用简单移动平均进行平滑处理。

周期拐点的判断方面，考虑到经济数据和资产收益数据在短期内都有可能突变和产生噪音，为了反映经济波动的真实趋势，本文周期判断的原则是参照道氏理论对趋势的判断方法，忽略小幅波动影响，以指标的趋势性变化作为拐点判断的主要依据。具体划分规则如下：指标变化必须达到一定的幅度，忽略每个指标较小幅度的波动。每个指标的上升周期：最低点为上升趋势的开始，最高点为上升趋势的结束，忽略中间的小幅波动。下降周期则相反。

2.3 我国经济周期的划分

按照以上方法，本文将我国的经济从2002年7月至2014年6月划分为两个经济周期当中的七个阶段。之所以截止到2014年是考虑到经济新常态下经济政策由需求管理到供给侧改革的重大变化。经济周期划分的具体结果见表3前两列。

2.4 大类资产在不同经济周期阶段的表现

为了对我国四类主要资产(股票、债券、商品、现金)在2002年7月到2014年6月间的实际收益表现进行考察，本文选取了四个被广泛应用的指数来代表四类资产。股票的代表指数为中证A股指数，债券的代表指数为中债综合财富指数(总值)，商品的代表指数为文华商品指数，现金的代表指数为全国银行间7天同业拆借利率的加权平均利率。由于本文是在较长周期上分析投资收益和风险的，同时国内外的类似研究多采用月收益率来衡量[9]，所以收益率的时间间距也采用了月收益率。利用上述四个指数，统计了四类资产在不同经济周期阶段的收益率均值，见表3。

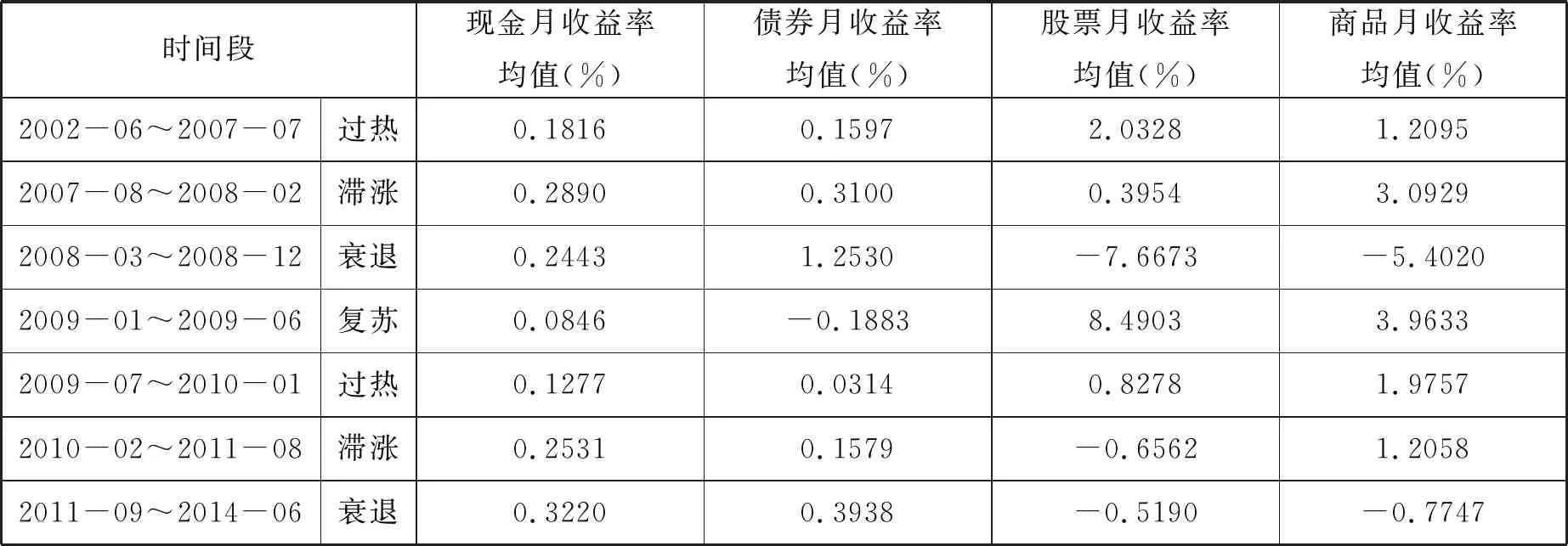
表3 我国各经济周期阶段上大类资产的收益率

通过以上数据可以看出，我国不同经济周期阶段资产收益率排序总体与美林投资时钟相类似。说明投资时钟现象在我国金融市场也是存在的，不同经济阶段各类资产的收益排序具有相对稳定性，在经济周期之间具有重复性和轮动表现。

3 实证分析

美林投资时钟对应的常见投资策略是轮动策略，在每一经济阶段选择投资时钟当中该阶段收益最高的资产进行投资。轮动策略仅考虑了收益因素，而没有考虑风险因素[10]。本文尝试把均值方差模型跟美林投资时钟相结合，对大类资产进行配置，通过回测跟轮动策略等常见策略的投资绩效指标进行比较，验证其有效性。

因为本文在较长周期上对经济阶段进行划分，考虑到大类资产代表指数收益率数据的可得性和前后一致性，所以只能在后一周期的三个阶段上进行回测。按照表3对我国经济周期的划分，回测在后一个周期的过热、滞涨、衰退三个阶段展开，时间区间为2009年7月到2014年6月。

首先对轮动策略进行回测，按照美林投资时钟模型，在过热、滞涨、衰退三个阶段上分别选取大宗商品、现金、债券进行投资，假设在每一经济阶段的第一个月份的第一天完成建仓，计算出回测区间的相关投资绩效数据见表4，该策略的平均月收益率为0.5338%。

均值方差模型回测同样假设在每一经济阶段的第一个月份的第一天完成建仓，计算前一周期当中三个经济阶段的各大类资产收益率的协方差，然后根据各阶段收益率均值和协方差运用MATLAB软件求出各阶段有效边界上的一些具体投资组合[11]。因为主要跟轮动策略进行对比，所以参照轮动策略的收益率，在每一经济阶段选取有效边界上月收益率为0.5338%的点所对应的具体配置比例在回测区间相应经济阶段进行配置，计算出回测区间的相关投资绩效数据，见表4。

上述轮动策略和均值方差模型都是基于投资时钟的主动型投资策略，作为和主动型管理策略相对的被动型管理策略，本文还计算了等权重策略的投资绩效数据，假设为了保持等权重策略要求的配置比例，每3个月调整一次配置比例，并且在调整月份的第一天完成建仓，计算结果见表4。

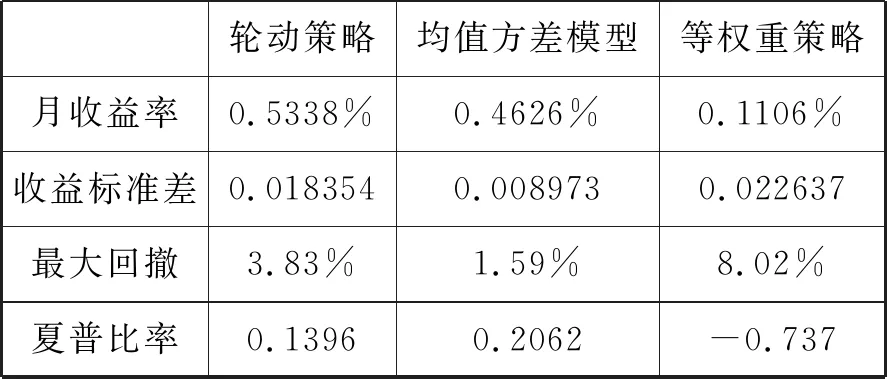
表4 各种策略回测结果比较

上述计算过程中，计算夏普比率所用的无风险利率为同期现金资产的月收益率，经计算为0.2775%。

通过对比可知，均值方差模型的收益率略低于轮动策略，表征风险的收益标准差、最大回撤都优于轮动策略，夏普比率则明显优于轮动策略。鉴于夏普比率综合考虑了收益和风险，是绩效评价的标准化指标，所以实证结果表明，在投资时钟框架下均值方差模型的综合表现是优于轮动策略的。均值方差模型的优势还体现在可调整性上，可以随时根据不同投资机构的收益目标或者风险目标来调整配置。被动型等权重策略在各方面的表现都逊色于基于投资时钟的前两个策略，也印证了投资时钟在我国资产配置中的有效性。

4 总结与探讨

本文的研究表明，美林投资时钟揭示了不同经济阶段大类资产的表现和相互关系，是能够帮助机构投资者进行积极有效的大类资产配置的，但是由于经济数据和资产收益都会受到一些短期不可预期的冲击，所以其具体应用不能机械地参照经典理论。本文在经济周期的划分方面，注重经济变化的真实趋势性，忽略了经济数据的短期波动，进行较长期的划分。根据回测检验，印证了在这种划分方法之下，经济周期性变化过程中大类资产的收益表现和相互关系具有相对稳定性，也证实了均值方差模型在美林投资时钟的框架下是能够动态运用的，并且可以获得良好的资产配置效果。

本文的研究结论对于理论研究和投资实践具有一定的指导意义，但是仍然存在很多不足，接下来的研究可以从以下几个方面进行深入和改进：首先，由于在较长周期内的数据的缺乏，为了保持资产代表指数数据的前后一致性，本文考察的经济周期没有包括完整的两个周期，相应的也只是回测了一个经济周期的三个阶段，牺牲了回测的周期完整性，因此可以从数据完整性和处理方法上进行改善，在更长周期上进行检验和回测。其次，本文只是考察了经典的均值方差模型在投资时钟框架下的应用，今后可以考虑把均值-半方差模型、均值-VaR模型、均值-CVaR、Black-Litterman模型和投资时钟理论相结合进行大类资产配置的研究。最后，投资时钟本身属于融入主观判断的资产配置策略，宏观经济走势和经济政策的变化错综复杂，经济的周期性变化也将会有不同的表现形式。本文仅将前一周期数据作为预测值纳入均值方差模型，如果能根据经济形势的变化对收益率均值和资产之间的相互关系进行预测，把预测值运用于模型，可能会提升模型的有效性，这就要求深入考察各类资产收益背后的产出周期、货币周期和利润周期的变化和相互关系。