回归分析中若干独立性的证明

易景平，蔡定教

(1.安阳师范学院 数学与统计学院，河南 安阳 455000；2.河南财经政法大学 数学与信息科学学院，河南 郑州 450046)

0 引言

正态线性回归模型

y=Xβ+e,e～N(0,σ2I)

中关于未知参数向量的一般线性假设

H:Aβ=b

检验问题中的检验统计量为

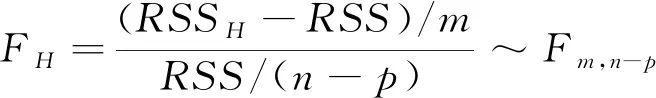
其中RSS为残差平方和,RSSH为约束条件下的残差平方和。其证明涉及到RSSH-RSS与RSS的独立性，一般的教材证明中利用了“ξ与η独立且ξ与ζ独立，则ξ与η+ζ独立”这一结论。虽然这一结论在很多情形下是成立的, 但利用文献[1]中的伯恩斯坦反例不难举例说明ξ与η独立且ξ与ζ独立并不蕴含ξ与η+ζ独立，本文将避开这一前提对RSSH-RSS与RSS的独立性加以严格的证明。利用相同的思路证明拟合值向量与学生化残差的独立性，并在最后给出一个判定两个向量独立性的充分性条件。

1 RSSH-RSS与RSS的独立性

这里我们假设设计阵X为列满秩矩阵，利用残差平方和的定义可得

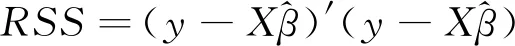
=y′(I-X(X′X)-1X′)y

=e′(I-X(X′X)-1X′)e

=e′Ne

其中N=I-X(X′X)-1X′为对称幂等阵。在约束条件

H:Aβ=b(这里假设A为行满秩矩阵)

之下, 由文献[2]知未知参数向量β的约束最小二乘估计为

从而约束条件下的残差平方和为

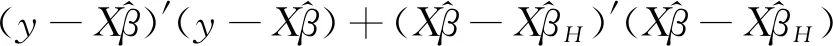
由于

=AX(X′X)-1X′e+(Aβ-b),故

RSSH-RSS

=e′X(X′X)-1A′(A(X′X)-1A′)-1AX(X′X)-1X′e

+2(Aβ-b)′(A(X′X)-1A′)-1AX(X′X)-1X′e

+(Aβ-b)′(A(X′X)-1A′)-1(Aβ-b))

=e′Me+a′e+c

其中

M=X(X′X)-1A′(A(X′X)-1A′)-1AX(X′X)-1X′

a′=2(Aβ-b)′(A(X′X)-1A′)-1AX(X′X)-1X′

c=(Aβ-b)′(A(X′X)-1A′)-1(Aβ-b)

易知M、N为对称阵且MN=0，从而NM=0，故有MN=NM,即M、N可交换。由文献[3]知可用一个正交阵Φ将M,N同时正交对角化, 即存在正交阵Φ使得

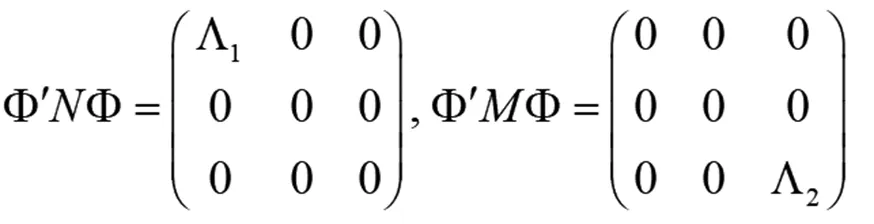
这里,

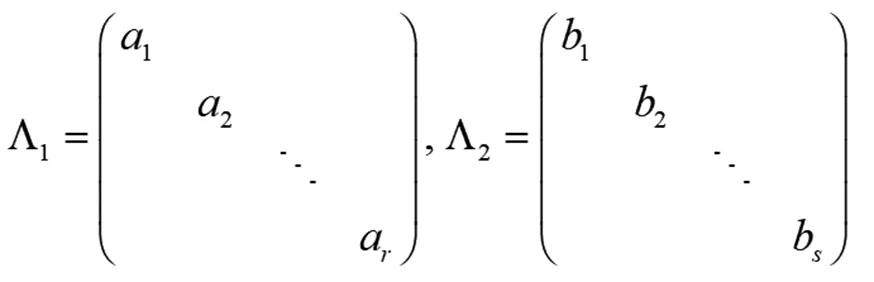
其中ai≠0，i=1,2,…,r；bj≠0,j=1,2,…,s；r+s≤n。

又a′N=0, 故a′ΦΦ′NΦ=0。令a′Φ=(c1,c2), 其中c1为1×r行向量, 则有c1Λ1=0,可得c1=0。由假设我们有e～N(0,σ2In), 这里不妨设σ2=1。令Y=Φ′e, 由文献[4]或文献[5]知Y～N(0,In), 记Y=(Y1,Y2,…,Yn)′, 则Y1,Y2,…,Yn相互独立。由

分析： 从分子机制上看，水稻的抗病反应需要水稻自身抗病蛋白(R系列)与MP蛋白(A系列)相匹配，进而结合，才能被激活。所以被a1a1A2A2a3a3的MP侵染后，只有 R2R2 类型的抗病反应才能被激活(图2)。因此，R1 R1r2r2R3R3和r1 r1R2R2R3R3分别表现为感病和抗病。

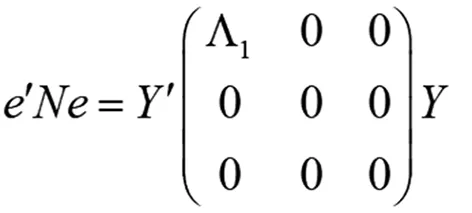
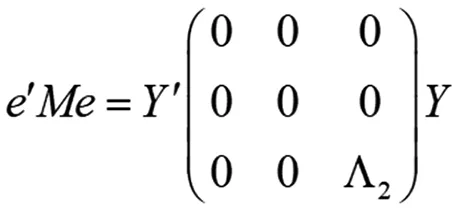
a′e=(0,c2)Y

知RSS为(Y1,Y2,…,Yr)的连续函数,RSSH-RSS为(Yr+1,Yr+2,…,Yn)的连续函数, 由文献[6]知RSS与RSSH-RSS相互独立。

2 拟合值向量与学生化残差的独立性

对于线性回归模型

y=Xβ+e,e～N(0,σ2In)

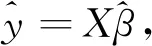
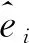
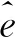
现设

其中Λ为(n-p)×(n-p)对角阵且Λ>0,X(X′X)-1X′Φ=(C1,C2),其中C1为p×(n-p)矩阵。由

X(X′X)-1X′ΦΦ′(I-X(X′X)-1X′)Φ=0

知C1=0。

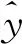
3 一个判定独立性的充分条件

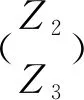
证明不妨设

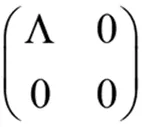
其中Λ为r×r对角阵且|Λ|≠0。

a1,a2,…,as,b1,b2,…,bt,c1,c2,…,cn-r-s-t

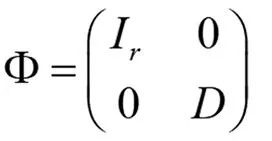
可知Φ为n×n正交阵。令Y=(Y1,…,Yr,Yr+1,…,Yr+s,Yr+s+t,…,Yr+s+t+1,…,Yn)=ΦX, 则Y～N(0,In), 故Y1,…,Yr,Yr+1,…,Yr+s,Yr+s+1,…,Yr+s+t,Yr+s+t+1,…,Yn相互独立。