高维广义具阻尼项的Bq方程解的整体存在性和衰减行为

李梅玲，王云青

( 渤海理工职业学院 基础部，河北 沧州 061199)

0 引言

本文主要考察下面一类Bq方程的柯西问题

utt-Δu-aΔutt+Δ2u+Δ2utt-bΔut

=Δf(u),x∈Rn,t>0

(1)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Rn

(2)

其中u(x,t)表示未知函数，u0和u1是给定的初始函数值，Δ是n维拉普拉斯算子，a,b>0为常数。很多数学家和物理学家研究了带有色散项或者耗散项的Bq方程的衰减[1-2]，但很少有人研究既带有色散项又带有耗散项的衰减结果。Wang等人给出了当a=b=1时此问题解的整体存在性和衰减行为[3]。Piskin等人研究了当a=2时上述问题解的整体存在性和衰减估计[4]。本文主要研究带有色散项和耗散项的Bq方程的柯西问题及衰减行为。

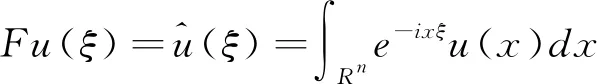
记号AB表示A≤CB，其中C>0为每一个常数的同一个标志。

1 对应线性方程解的衰减估计

研究下面线性问题解的衰减性

utt-Δu-aΔutt+Δ2u+Δ2utt-bΔut

=Δg(x,t)，x∈Rn,t>0

(3)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈Rn

上述问题的形式解为

u(x,t)=H(t)u0+G(t)u1

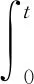
(4)

格林算子

G(t)=F-1L(ξ,t)F，H(t)=F-1L1(ξ,t)F

其特征是

其中ω(ξ)=

(5)

为估计线性问题的衰减性，引入m阶Bessel函数Jm(r)的一些性质[5]，径向函数f(x)=f(|x|)的傅里叶变换仍然是一个径向函数，且

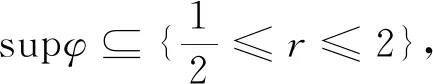
引理1[3]假设φj(ξ)=φ(2-jξ)，supφj⊆{ξ:2j-1≤|ξ|≤2j+1}，ω(ξ)=ω(|ξ|),由(5)式定义，则当j≤0时，下面不等式成立

(6)

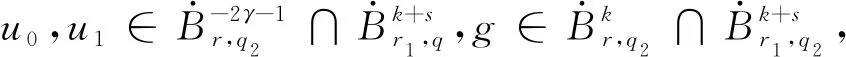
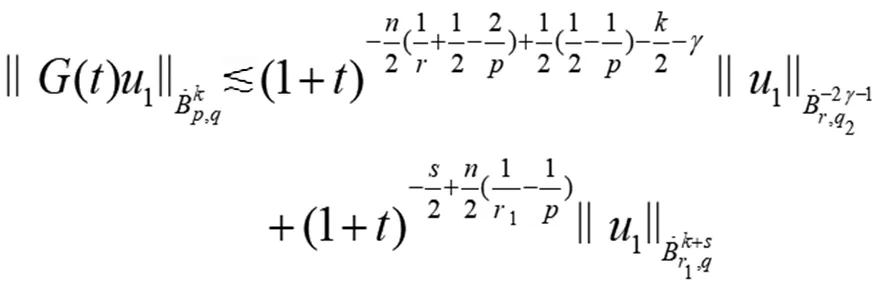
(7)

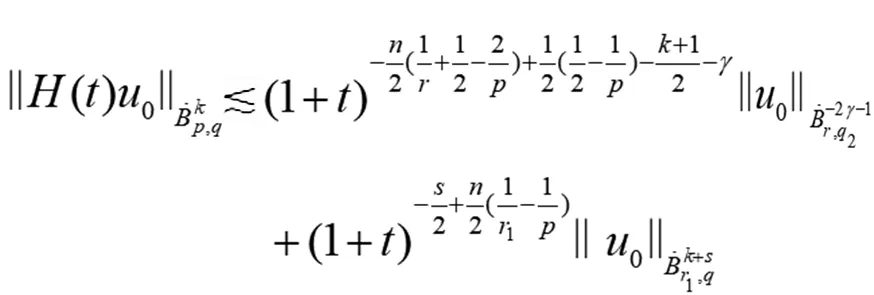
(8)

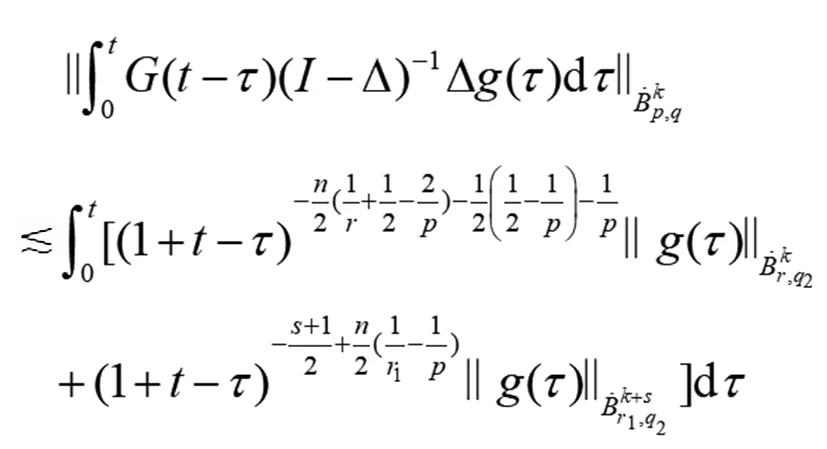
(9)

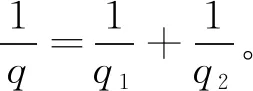
证明由齐次Besov空间的范数定义知，对∀u1∈S，有

对于A1，由Bernstein不等式和Young不等式，注意到ξ∈supφj⊆{ξ:2j-1≤|ξ|≤2j+1}，有

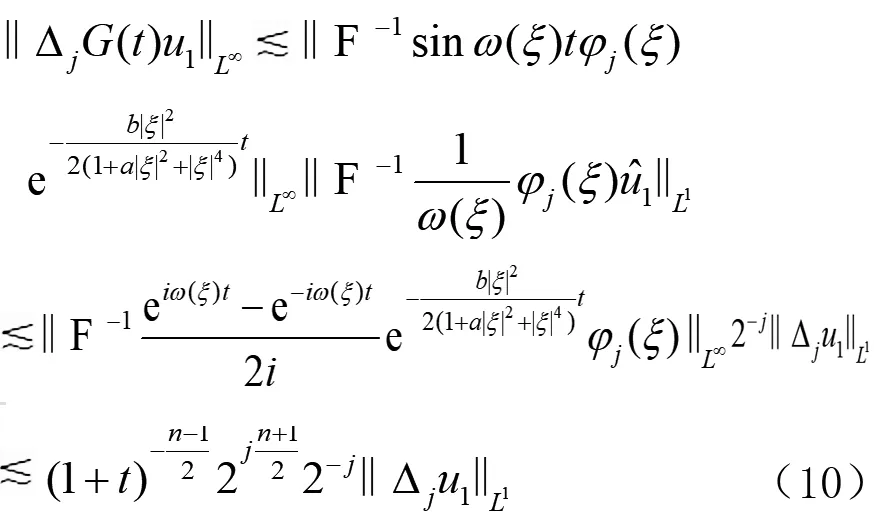
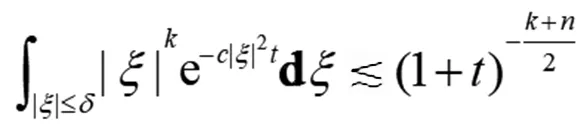
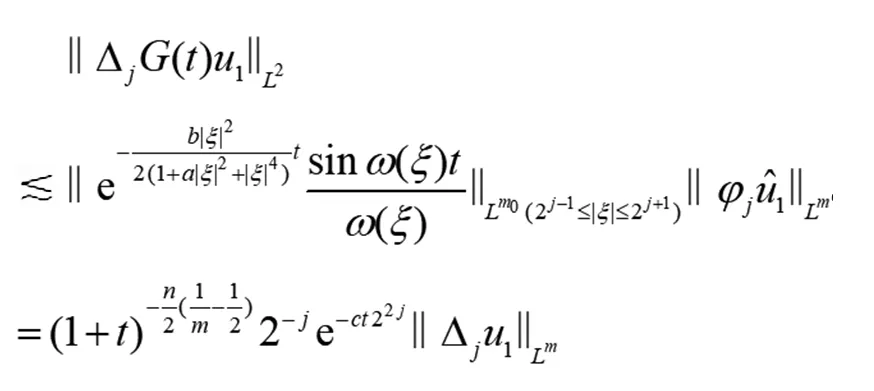
(11)

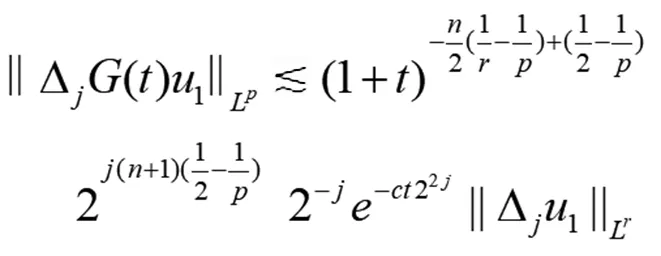
(12)

(12)式两边乘以2jk后，再取Lp范数(j≤0)，得

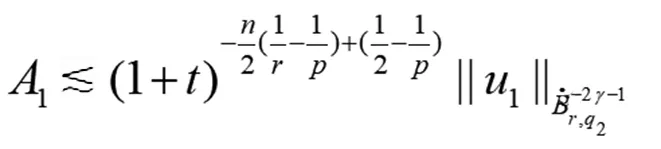
(13)

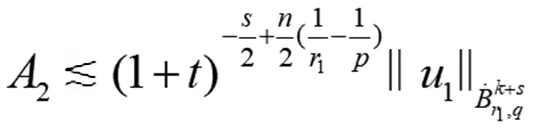
(14)

类似方法可证(8)和(9)式。

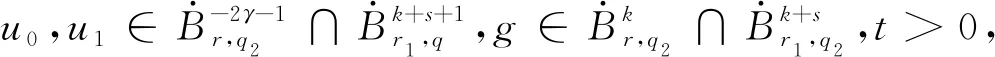
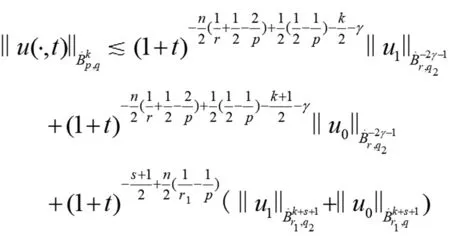
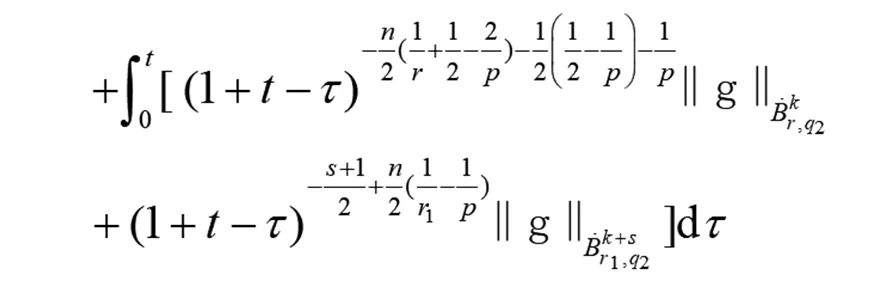
(15)

(16)

证明由杜哈密顿原理，易得问题(1)、(2)解的存在唯一性。(15)式由定理1和(4)式可得。因为

ut(x,t)=Ht(t)u0+Gt(t)u1

类似于定理1可证(16)式。

2 主要结果

引理2[3]对任意s≥0，f∈C{s}(R)，满足条件

|f(j)(u)||u|α-j,j=0,1,…,{s},{s}≤α

(17)

则对∀u∈R，有

(18)

引理3[6]假设a,b为两个正数，则

(19)

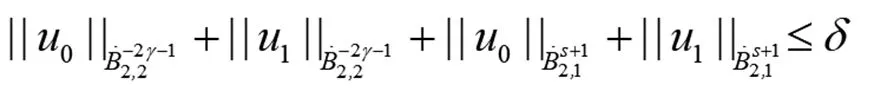
(20)

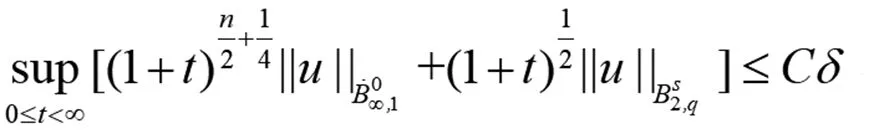
(21)

其中常数C只依赖于f。

证明首先，我们定义空间(X,d)上的非线性映射N

N(u)=H(t)u0+G(t)u1

(22)

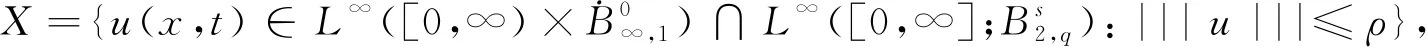
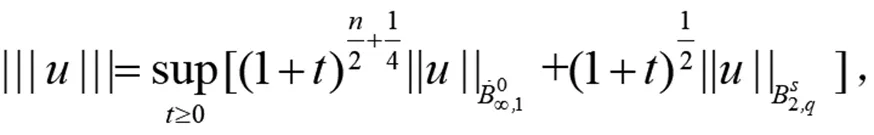
且对∀u，v∈X。d(u,v)=‖u-v‖L∞([0,+∞);L2)。易证，(X，d)是一个完备度量空间。

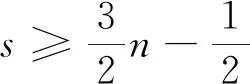
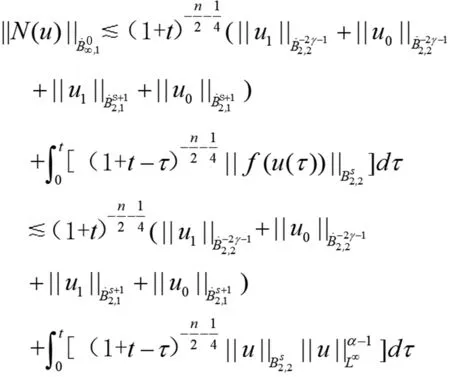
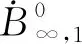
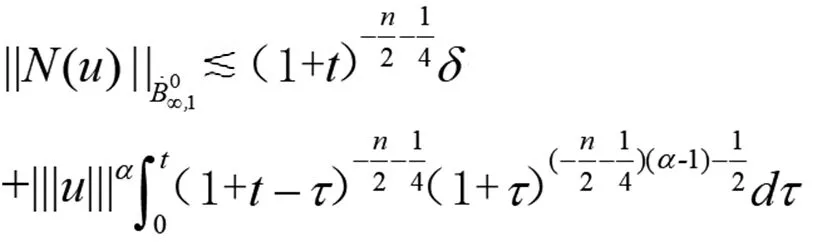
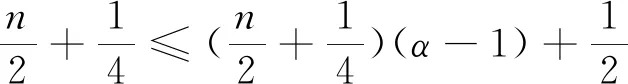
(23)

(24)

(25)

由(24)式和(25)式，有

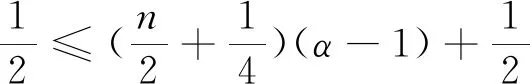
(26)

对∀u，v∈X,由(22)式，知

N(u)-N(v)

在(15)式中取k=0,s=0,p=2,q=q2=2，r1=r=2,得

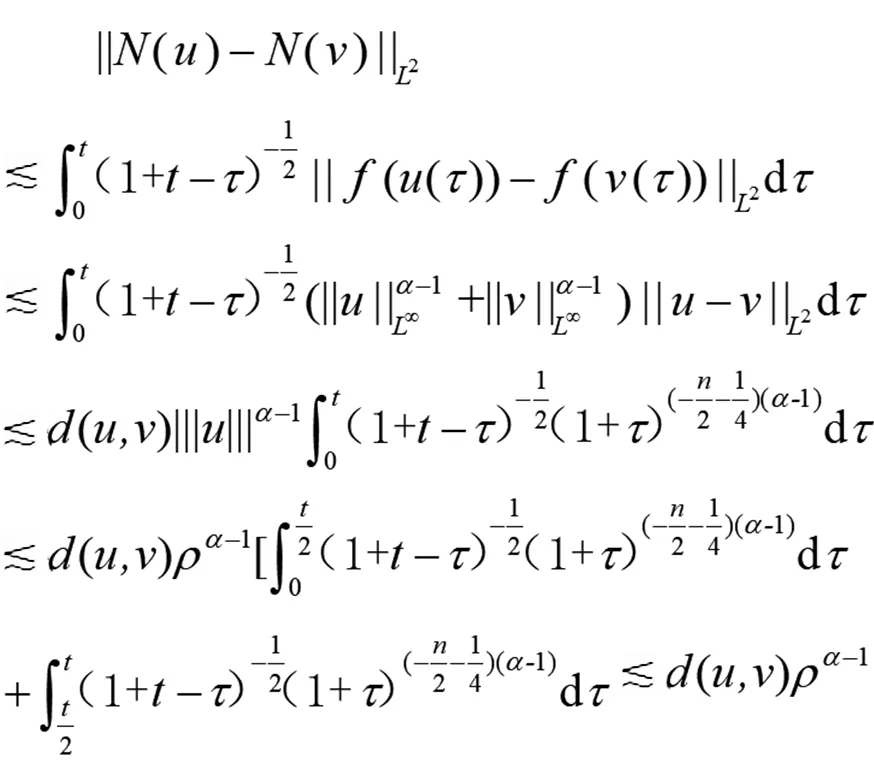
即对充分小的ρ，N是X到自身的严格压缩映射。利用压缩映射原理，知N(u)在X上存在唯一不动点u(x,t)，u(x,t)是问题(1)、(2)的解，且

u(x,t)=H(t)u0+G(t)u1

由标准理论可得到解u(x,t)的时间连续性。